在线自学习两轮轮式机器人点镇定仿人智能控制
王牛1, 2,张琦1,丘柳东1,杨祖元1,李祖枢1
(1. 重庆大学 智能自动化研究所,重庆,400030;
2. 东北大学 自动化研究中心,辽宁 沈阳,110004)
摘要:针对两轮轮式机器人点镇定控制中的实时优化问题,提出在线自学习点镇定仿人智能控制方法。该方法构建了一个3层控制结构,基于仿人智能多模态比例控制器,利用多神经网络分别进行各控制模态下的控制参数实时优化,采用模态切换控制器实现各模态及其学习优化模块的切换。通过仿真和实验,将所提出的控制方法与常规多模态控制方法进行比较,证实所提出方法的有效性。
关键词:点镇定;仿人智能控制;BP神经网络;在线自学习
中图分类号:TP391.9 文献标志码:A 文章编号:1672-7207(2011)S1-0498-07
Point stabilization control for two-wheel robot with online self-learning human simulated intelligence control
WANG Niu1, 2, ZHANG Qi1, QIU Liu-dong1, YANG Zu-yuan1, LI Zu-shu1
(1. Institute of Intelligent Automation, Chongqing University, Chongqing 400030, China;
2. Research Center of Automation, Northeastern University, Shenyang 110004, China)
Abstract: For the real time optimization during point stabilization control of two-wheel robot, a 3-layer control structure was proposed. The structure is based on the multi-mode human simulated intelligence controller (HSIC). The parameters of different mode controller are optimized by the specific BP neural networks. The controllers, learning-modules and optimizing-modules are switched by mode switch controller. Comparing with regular multi-mode controller, the validity of the control approach is confirmed through simulation and real system tests.
Key words: point stabilization; human simulated intelligence control; BP neural network; online self-learning
到定点的问题是机器人底层控制的基本问题,即点镇定问题。点镇定也称为位姿镇定、姿态跟踪或设定点调节,其问题描述如下[1]:给定任意位置Pr:(x, y),设计机器人速度控制输入vc=fc(e, w, K, t),其中e, w, K分别为位置误差,参考速度矢量和控制增益矢量,为使得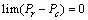 ,计算力矩τ(t)使t→∞,vr→vc。
,计算力矩τ(t)使t→∞,vr→vc。
由于两轮轮式机器人存在非完整运动约束,不满足Brockett光滑联系镇定的必要条件,只能通过设计连续定常控制律、时变控制律或混合控制律来实现其点镇定控制[2-4]。董文杰等[5-9]借助非线性控制理论或反馈线性化等方法设计了不同的光滑时变或非连续的反馈控制律,将具有非完整约束的系统转变为链式系统或线性的解耦系统,然后设计满足性能要求的控制律。王超越等[10]进一步提出一种基于人工势场进行导向与控制的非连续位姿镇定方法,考虑了速度饱和限制和电机输出力矩的影响,取得了较好的效果。本文作者也根据典型双闭环轮速跟随运动执行系统的实际机器人,运用仿人智能控制理论,设计实现了利用遗传算法离线整定参数的多模态切换点镇定控制器,取得了较好的效果[11]。然而,由于运动的初始状态对于控制的效果具有很大的影响,一组控制参数很难适用于各种不同的初始状态;同时,在实际运动控制过程中,因为机器人电池电量下降,碰撞、摩擦和运动执行系统老化等因素造成被控对象模型发生变化,使机器人的运动控制性能下降,难以保证较优的控制效果,甚至可能导致系统失控,因此,需要进一步针对机器人运动控制器进行实时的调整。刘金坤[12]提出了基于BP神经网络整定的PID控制方法。该方法以慢时变对象作为被控对象,在线整定基于经典增量式数字PID控制器的参数,获得了不错的效果。但是,该系统是一个单输入单输出的系统,并非两轮轮式机器人这样的多输入多输出系统。针对上述问题,本文作者提出了一种在线自学习两轮轮式机器人点镇定仿人智能控制方法,构建了一个3层控制系统结构,以解决多输入多输出控制系统的多模态控制器的在线优化控制问题,实现了具有非完整约束两轮轮式机器人点镇定在线自学习控制,并进行了仿真和实际系统实验。
1 控制系统结构
机器人运动控制系统主要由控制器、电机驱动模块、反映机器人运动机构特性的运动学模块、位姿反馈模块组成,如图1所示。其中:控制器为一个3层控制结构,底层为多模态的仿人智能控制器;中层利用多个BP神经网络分别对应各底层控制模块,实现各模态控制器参数的在线自学习优化;最上层为模态切换控制器,通过产生式规则实现各控制模态及其在线自学习优化模块的切换。
2 多模态HSIC控制器
HSIC采用基于特征模型的多模态控制策略,模仿人的控制决策行为,确定机器人所处的特征状态,采取相应的控制策略,使得该方法具有智能特性,能较好地实现点镇定控制。控制器模态划分采用文献[13]中提出的设计准则,如图2所示。
图2中Ed为距离偏差时目标点相对于机器人的距离;Er为机器人所处位置到目标点的方向与机器人朝向间的角度偏差。根据Ed和Er的不同划分为4个模态;θ1,θ2和d1分别为划分模态的角度偏差阈值和距离偏差阈值。图1中的神经网络参数整定模块NN由4个BP神经网络组成,分别对应HSIC控制器的4个模态。每个BP神经网络输出对应模态的角速度控制参数Kr。
HSIC控制器各个模态控制律分别为:
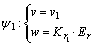
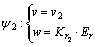
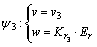
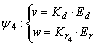 (1)
(1)
式中:v1,v2,v3和Kd采用固定值;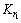 ,
,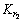 ,
,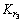 和
和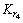 为需要进行在线自学习优化的控制参数。
为需要进行在线自学习优化的控制参数。
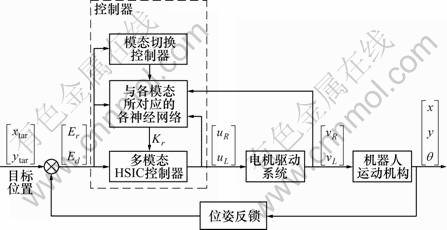
图1 控制系统框图
Fig.1 Block diagram of control system

图2 控制模态
Fig.2 Control mode
3 基于多BP神经网络的在线自学习优化
本研究采用文献[14]中提出的BP神经网络的Specialized Learning算法,该算法利用实际输出与理想输出的差值来改变神经网络各层的权值,从而避免了离线训练步骤,这样,就可以根据被控对象的输出进行在线估算来学习和调整神经网络。
对于提出的控制器,与图2所划分的模态相适应,采用4个BP神经网络对应着HSIC控制的4个不同模态来进行角速度的参数自整定。BP神经网络的结构同为3-5-1,BP神经网络结构如图3所示。
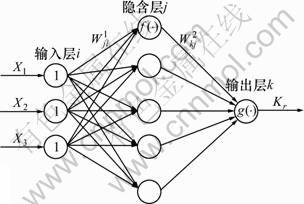
图3 神经网络结构
Fig.3 Structure of neural network
其中输入层节点到隐含层节点的连接权用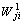 表示;隐含层节点到输出层节点的连接权用
表示;隐含层节点到输出层节点的连接权用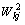 表示。用f(·)表示输入层到隐含层的激活函数;用g(·)表示隐含层到输出层的激活函数。图3每一层的输入输出如下:
表示。用f(·)表示输入层到隐含层的激活函数;用g(·)表示隐含层到输出层的激活函数。图3每一层的输入输出如下:
输入层输入:
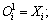 i=1, 2, 3 (2)
i=1, 2, 3 (2)
隐含层输入:
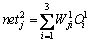 (3)
(3)
隐含层输出:
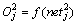 (4)
(4)
输出层输入:
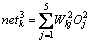 (5)
(5)
输出层输出:
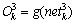 (6)
(6)
隐含层神经元的激活函数为正负对称的Sigmoid函数:
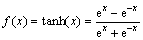 (7)
(7)
输出层神经元的激活函数为非负的Sigmoid函数:
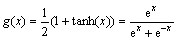 (8)
(8)
取性能指标函数为E(k)(其中k为时间变量):
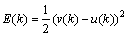 (9)
(9)
为了加快BP网络收敛到局部极值,在权值修正时引入动量项,即:
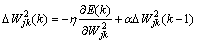 (10)
(10)
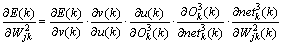 (11)
(11)
其中:η为学习效率因子;α为动量因子。由于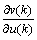 未知,所以,用近似符号
未知,所以,用近似符号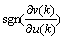 取代,由此带来
取代,由此带来
计算不精确的影响可以通过调整学习速率来补偿。
以下为4个模态对应的BP神经网络的输入和输出。
f1模态的输入:
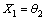 ,
,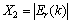 ,
,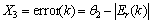 (12)
(12)
f1模态的输出:
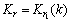 (13)
(13)
f2模态的输入:
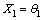 ,
,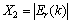 ,
, (14)
(14)
f2模态的输出:
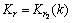 (15)
(15)
f3模态的输入:
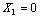 ,
,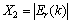 ,
,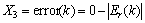 (16)
(16)
f3模态的输出:
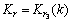 (17)
(17)
f4模态的输入:
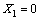 ,
,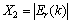 ,
,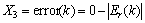 (18)
(18)
f4模态的输出:
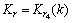 (19)
(19)
在4个模态中,输入的error都是以角度偏差的阈值减去角度偏差的绝对值,目的是希望通过权值的反向修正促使模态可以迅速地切换向着目标点前进。
4 基于产生式规则的模态切换
根据图1对角度和距离偏差空间进行的模态划分有:
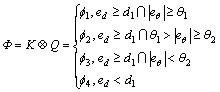 (20)
(20)
采用IF-THEN形式建立产生式规则集:
IF fi THEN ψi;i=1, 2, 3, 4 (21)
同时,启动对应的参数自学习优化神经网络进行控制器ψi控制模态参数的优化。
5 仿真与实验
5.1 实验设计
5.1.1 仿真测试实验设计
在文献[11]建立的机器人运动控制仿真系统基础上,通过遗传算法得到控制器控制参数为:v3 =1 600 r/min,v2 =1 336.3 r/min,v1=276.1 r/min,Kd=0.2,θ2= 90?,θ1=25.8?,d1=1 500 mm, 再加入神经网络进行在线参数整定。系统仿真步长为50 ms,共200步。以NN-HSIC表示所提出方法,以MP表示通过遗传算法进行离线参数整定的多模态控制方法。
主要测试内容:以坐标原点8个方向上的8个点以及2个特殊点共10个点即(4 000, 4 000),(4 000, 0),(4 000, -4 000),(0, -4 000),(-4 000, -4 000),(-4 000, 0),(-4 000, 4 000),(0, 4 000),(10 000, 50),(50, 10 000)作为测试目标点,比较控制效果。
然后,在实验中让左电机的参数β和K在一定范围内按指数函数变化。考虑到机器人的实际电机情况,β的变化范围由100%至50%,K的变化范围为100%至150%:
β通过指数函数变化:
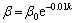 (22)
(22)
K通过指数函数变化:
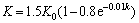 (23)
(23)
其中:β0和K0为电机性能常数;k为时间变量。
在模型发生变化的情况下,将所提出的方法与MP方法的控制效果作对比。
主要测试指标如下:
①可达。通过得到的运动轨迹以及在规定时间10 s,即200步内到达目标点作为判断主要依据,10 s内能到达即为可达。
②到达目标点的时间。通过得到的运动轨迹,计算进入目标领域500 mm内的时间作为达到目标点时间。
5.1.2 实际系统测试
采用实际机器人系统进行实验,观察实际控制效果。
5.2 数据分析
5.2.1 仿真比较
仿真效果如表1所示,本文作者所提出的方法在5个点的时间上短于MP方法,时间最多提前24步,最多落后18步。总体上2种方法的效果差不多。表2中,本文所提出的方法全部10个点可达,且除去MP不可达的4点之外的6个点共有4点时间短于另一种方法。与表1相比,NN-HSIC方法在表2相同点的时间延后49步,另一种方法延后100步。证明了在模型变化的情况下,本文作者所提出的方法更有效。
5.2.2 实际系统测试
图4~7所示为实际控制效果。其中,图4所示为NN1和NN2分别为模型不变和模型发生变化情况下,到指定点控制效果;图5所示为对应实际机器人运动控制效果,其运动趋势与仿真相一致; 图6所示为实际运动过程中各模态学习控制参数的学习过程,实线表示对应模态中参数整定起作用部分,虚线表示对应模态参数整定不起作用部分。
表1 系统模型不变情况下控制效果比较
Table 1 Comparison of control effect on condition when system model is constant
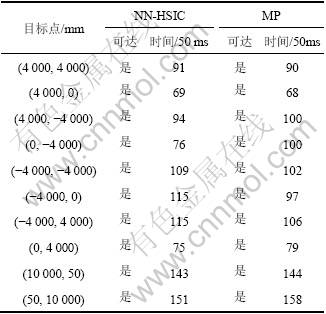
表2 系统模型变化情况下控制效果比较
Table 2 Comparison of control effect on condition when system model is changed
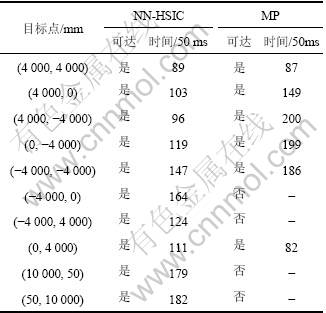
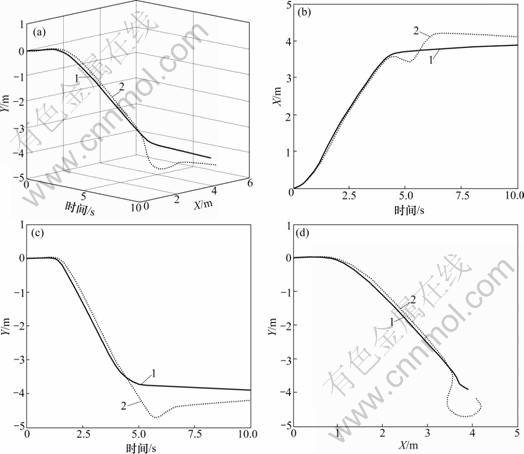
图4 采用NN-HSIC控制算法到点(4 000, -4 000)仿真
Fig.4 Simulation results with NN-HSIC control algorithm to point (4 000, -4 000)
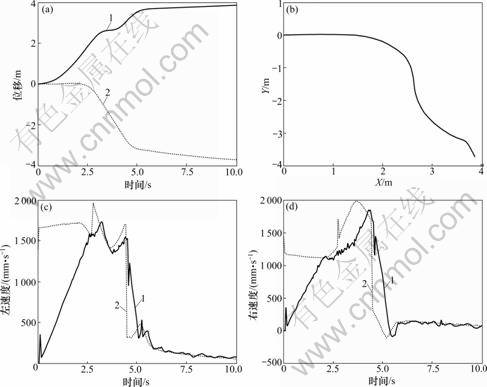
图5 实际机器人到点(4 000, -4 000)控制效果
Fig.5 Control effect of fact robot to point (4 000, -4 000)
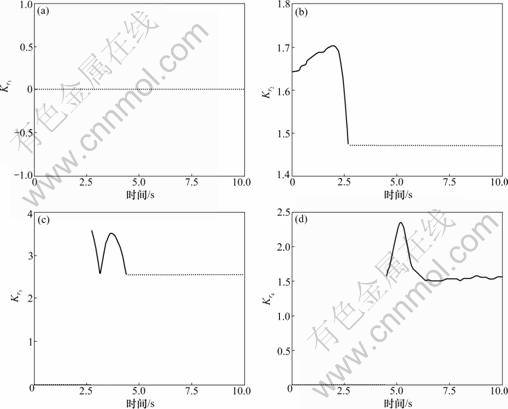
图6 实际机器人运动过程中各控制模态对应神经网络的学习过程及控制模态切换情况
Fig.6 Neural networks parameter learning process and control modes switch in process of fact robot’s move

图7 用于实验的实际机器人
Fig.7 Fact robot for experiment
6 结论
提出一种在线自学习点镇定仿人智能控制方法,构建具有3层控制结构的控制器,底层为多模态仿人智能控制器;控制参数优化层采用了多个BP神经网络,通过Specialized Learning算法进行控制参数的自学习;上层采用了1个与模态划分相一致的基于产生式规则的模态切换控制器实现各模态及其参数优化神经网的切换。通过仿真对比和实际系统的实验证明了所提出控制方法的有效性。
参考文献:
[1] 王越超, 景兴建. 轮式移动机器人控制[J]. 机器人, 2000, 22(7): 724-729.
WANG Yue-chao, JING Xing-jian. Control of wheeled mobile robot[J]. Robot, 2000, 22(7): 724-729.
[2] Kolmanovsky I, Mcclamroch N H. Developments in nonholonomic control problems[J]. IEEE Control System Magazine, 1995, 15(6): 20-36.
[3] Brockett R W. Asymptotic stability and feedback stabilization [C]//Differential Geometric Control Theory. Boston: Birkhauser, 1983: 181-208.
[4] 唐述博. 非完整机器人点镇定和轨迹跟踪控制研究[D]. 大连: 大连理工大学控制科学与工程学院, 2005: 11-13.
TANG Shu-bo. Point stabilization and trajectory tracking control on nonholonomic mobile robot[D]. Dalian: Dalian University of Technology, School of Control Science and Engineering, 2005: 11-13.
[5] 董文杰, 霍伟. 链式系统的轨迹跟踪控制[J]. 自动化学报, 2000, 26(3): 310-316.
DONG Wen-jie, HUO Wei. Trajectory tracking control of chained systems[J]. Acta Automatica Sinica, 2000, 26(3): 310- 316.
[6] Sordalen O J, Egeland O. Exponential stabilization of nonholonomic chained systems[J]. IEEE Transaction on Automatic Control, 1995, 40(1): 35-49.
[7] Park K, Chung H, Lee J G. Point stabilization of mobile robots via state-space exact feedback linearization[J]. Robotics and Computer Integrated Manufacturing, 2000, 16(5): 353-363.
[8] Mukherjee M, Chen D G, Song G B. Feedback control strategies for a nonholonomic mobile robot using a nonlinear oscillator[J]. Journal of Robotic Systems, 1999, 4(16): 237-248.
[9] Samson C. Control of chained systems-application to path following and time-varying point-stabilization of mobile robots[J]. IEEE Transactions on Automation Control, 1995, 40(1): 64-77.
[10] 王越超, 景兴建. 非完整约束轮式移动机器人人工场导向控制研究[J]. 自动化学报, 2002, 28(5): 777-783.
WANG Yue-chao, JING Xing-jian. Steering and control of nonholonomic wheeled mobile robots using artificial fields[J]. Acta Automatica Sinica, 2002, 28(5): 777-783.
[11] 王牛, 李祖枢. 一种两轮轮式机器人点镇定智能控制实现[J]. 控制理论与应用, 2010, 27(4): 437-443.
WANG Niu, LI Zu-shu. Realization of point stabilization intelligence control for two-wheel robot[J]. Control Theory & Applications, 2010, 27(4): 437-443.
[12] 刘金坤. 先进PID控制及其MATLAB仿真[M]. 北京: 电子工业出版社, 2003: 96-104.
LIU Jin-kun. Advanced PID control and MATLAB simulation [M]. Beijing: Publishing House of Eletronics Industry, 2003: 96-104.
[13] 王牛. 基于动觉智能图式足球机器人运动控制[D]. 重庆: 重庆大学自动化学院, 2008: 102-114.
WANG Niu. Research of soccer robot human simulated intelligence motion control based on sensory-motor intelligence schema[D]. Chongqing: Chongqing University. College of Automation, 2008: 102-114.
[14] Saerens M, Soquet A. Neural controller based on back- propagation algorithm[J]. IEEE Proceedings F (Radar and Signal Processing), 1991, 138(1): 55-62.
(编辑 何运斌)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:国家自然科学基金资助项目(60804018);中央高校基本科研业务费资助项目(CDJZR10170008);重庆市科委自然科学基金资助项目(CSTC2010BB2237);重庆大学引进人才科研启动基金资助项目(CQU0903005101636)
通信作者:王牛(1974-),男,重庆人,博士后,从事智能控制、智能机器人、复杂系统控制、模式识别与图像处理的研究;电话:13983943208;E-mail:wangniu@cqu.edu.cn