J. Cent. South Univ. (2018) 25: 1251-1262

DOI: https://doi.org/10.1007/s11771-018-3822-8

Evaluation on prediction abilities of constitutive models considering FEA application

WEN Tong(温彤), LIU Lan-tao(刘澜涛), HUANG Qian(黄倩), CHEN Xia(陈霞), FANG Ji-zhao(方继钊)

College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: Constitutive model plays an important role in the numerical simulations of metal forming. However, the influence of the models on the calculation is vague. Based on the stress–strain data of Al 7050 and Ti–6Al–4V alloys generated by isothermal compressive tests, the Johnson-Cook (JC) and Arrhenius-type (A-type) hyperbolic sine models were fitted to obtain the constants. Flow stresses directly calculated by the equations were compared with the experiment results, and rigid-plastic finite element analyses (FEA) utilizing these models were employed to simulate the same compression processes. The results show that A-type model has higher accuracy in the direct prediction of flow stress, even outside of the fit domain. The simulation results using A-type model also have higher agreement with the experiment; however, the suitability is affected by the referential parameters employed in the regression process. In terms of the overall deformation and strain distributions, there are slight differences among the simulation results using these two models.

Key words: constitutive model; metal forming; numerical simulation; performance; isothermal compression

Cite this article as: WEN Tong, LIU Lan-tao, HUANG Qian, CHEN Xia, FANG Ji-zhao. Evaluation on prediction abilities of constitutive models considering FEA application [J]. Journal of Central South University, 2018, 25(6): 1251–1262. DOI: https://doi.org/10.1007/s11771-018-3822-8.

1 Introduction

In the study of metal forming, it is of great importance to construct constitutive models that can accurately describe the plastic flow behaviors of materials. For example, constitutive models play an important role in the numerical simulation—so far the most powerful tool for analyzing the forming processes. Essentially, constitutive models reflect the quantitative relationship between the strength of material and the deformation parameters such as strain, strain rate, and temperature. Unlike cold deformation, the rheological behaviors of metallic materials at elevated temperature are associated with various interconnecting complex metallurgical phenomena, such as work hardening, dynamic recovery (DRV), dynamic recrystallization (DRX), flow instability, and dynamic strain aging. Therefore, in the establishment of constitutive models, these factors should be properly taken into account to obtain an acceptable result [1, 2].

To date, various analytical, phenomenological, and empirical models have been proposed [3–9]. Among these models, the empirical and semi- empirical models are the most preferred in the finite element analysis (FEA) of metal forming processes due to their usability. So far, the most commonly used models include the Johnson-Cook (JC) [3, 4], Arrhenius-type (A-type) [5, 6] and Zerilli-Armstrong (Z-A) models [7–9], as well as their extended forms [10–17]. In recent decades, extensive studies have been conducted on these models for a wide variety of ferrous and non-ferrous metals [18–24]. Currently, in order to formulate the constitutive relations of given materials, parameters of the models are calculated by fitting a series of experimental data from uniaxial compressive or tensile tests [25, 26]. Due to the strong nonlinear characteristics of thermal deformation of metals, the existence of fitting errors is inevitable. Therefore, an accurate description of the material response over a wide range of loading environments is very important. However, in many existing studies only specific experimental results are considered, meanwhile the influence of constitutive models on the numerical simulation is unclear.

In recent years, statistical methods from artificial intelligence like neural networks that treat the process as a black box have also been used to predict the hot flow behaviors of metals [27–29]. Although the methods are powerful in dealing with problems with highly nonlinear characteristics, they are difficult to utilize directly in FEA and thus cannot give valid guidance for practice, since no specific analytical equation is obtained. Furthermore, they offer no physical insight [28].

The goal of the current study is to establish a reliable approach for comprehensively evaluating the performance of the constitutive models, from the perspective of direct comparison and, especially, the application in numerical simulation. Two widely used constitutive models, namely the JC and A-type hyperbolic sine models, were constructed using the data from a series of isothermal compressive tests. Flow stresses of the materials were directly calculated using the models, and the predicted data were compared with the independent experimental results. Then, the models were input into FEM codes to simulate the compression processes, and the stress distributions calculated were compared with the experimental and analytical results to examine the performance of these modes.

2 Construction of constitutive equations for Al 7050 and Ti–6Al–4V

2.1 Experiment procedure

The isothermal compressive tests that follow a typical procedure were conducted on a Gleeble- 1500 thermo-simulator. 7050 aluminum alloy and Ti–6Al–4V titanium alloy with chemical compositions (wt%) of Al–6.1Zn–2.2Mg–2.3Cu– 0.31Fe–0.30Mn–0.16Cr and Ti–6.5Al–4.1V– 0.16O–0.21Fe–0.03C–0.015N–0.002H, respectively, were used in the study as received.

The columnar specimens were made by wire- electrode cutting method with a diameter of 10 mm and length of 15 mm. To reduce the friction between the surfaces of the anvils and the specimens, a mixture of machine oil and graphite was employed as lubricant. The specimens were compressed in a vacuum environment with a maximum reduction of 60% in height (true strain of 0.916), strain rates of 0.01, 0.1, 1, 3 and 10 s^–1, and temperatures of 523, 573, 623, and 673 K for Al 7050 and 1053, 1103, 1153 and 1203 K for Ti–6Al–4V, respectively. All specimens were resistance heated to the deformation temperature with heating rates of 3 K/s for Al 7050 and 10 K/s for Ti–6Al–4V and then held at that point for 90 s to ensure a uniform initial temperature distribution and reduce the material anisotropy after heating. The tests were repeated two or three times under each condition, and the compressed specimens with more symmetrical geometry were utilized as the final results.

The experimental results of flow curves will be presented in the next part with the theoretically predicted data.

2.2 JC Model

The original JC model considers the relationship between stress and strain, strain rate, and deforming temperature. It can be expressed as [2, 3]:

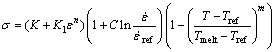 (1)

where the three parts on the right side of the equation represent the influence of material hardening, strain rate hardening, and temperature on the flow stress, respectively.

Next, experimental data of the flow stresses except for those at the strain rate of 3 s^–1 were used to fit the models for the two materials. The handling procedure has been presented in several literatures [26–29], so it will not be described in detail.

For Al 7050, the average melting temperature T_melt is 852.5 K, the reference temperature T_ref is 523 K, and the reference strain rate 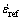is set to 0.01 s^–1. Under such circumstances, the yield stress K is 52.731 MPa. Therefore, according to the JC model, the relationship between the stress and strain, strain rate, and temperature of Al 7050 can be established as:

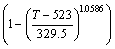                      (2)

For Ti–6Al–4V, T_melt is 1640 K, the reference temperature T_ref is 1053 K, the reference strain rate 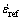is 0.01 s^–1, and the yield stress K is 104.51 MPa. Then, the equation of the JC model for Ti–6Al–4V can be established as:

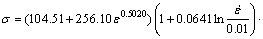
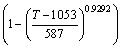                    (3)

2.3 A-type model

The A-type model shows the relationship among the hot deformation activation energy Q, strain rate 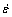, deforming temperature T, and flow stress σ. The model can be expressed as [10–12]:

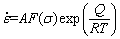                       (4)

where F(σ) is a function of the flow stress. For different levels of stress,

, ασ<0.8                          (5)

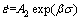, ασ>1.2                     (6)

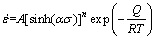, for all σ          (7)

The impact of strain rate and temperature on the deformation can be described by the Zener- Hollomon parameter Z, a coefficient for the temperature-compensated strain rate:

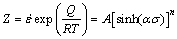               (8)

Combining Eq. (7) with Eq. (8), an explicit form of the flow stress can be obtained as:

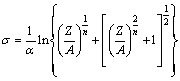              (9)

In the original A-type constitutive equation, the influence of strain on the deformation is not directly involved. To take this into account, the strain can be incorporated in the model by expressing the hot forming parameters (n, Q, α and A) as functions of strain [30]. The fifth-order polynomial functions of each coefficient can be written as:

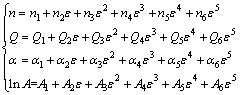     (10)

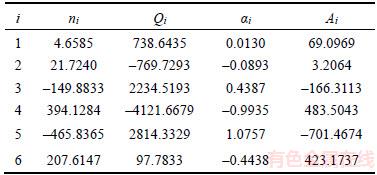
The coefficients of n, Q, α, and A can be worked out as shown in Tables 1 and 2. Figure 1 shows the results of the fifth-order polynomial fitting. Then, the values of each item at varying deformation temperature and strain rate can be obtained and the flow stresses can be worked out using Eq. (9).

Table 1 Coefficients of polynomial functions of Al 7050

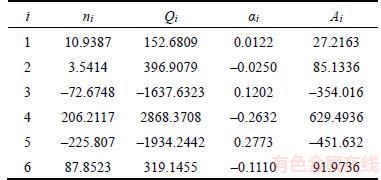
Table 2 Coefficients of polynomial functions of Ti–6Al–4V

3 Evaluation of direct prediction abilities of models

During the metal forming processes, varying deformation states frequently emerge due to the complex and inhomogeneous characteristics. Investigations have shown that the JC model is inadequate for providing a good description of the flow behavior despite being convenient to use, whereas the A-type equation could track the deformation behavior more accurately, but it requires more material constants and computational time [25, 26]. Nevertheless, these studies discussed the capability of constitutive models with true strain of less than 0.5 [25, 26, 31]. In the following, a relatively wide forming domain has been employed to examine the predicted accuracy of the JC model and A-type model for Al 7050 and Ti–6Al–4V. Unlike the methods used in many literatures, where the same group of experimental data used to determine material constants has been used again to show agreement with the same constitutive model [2], we compared the predicted data with the independent experimental results with a strain rate of 3 s^–1.

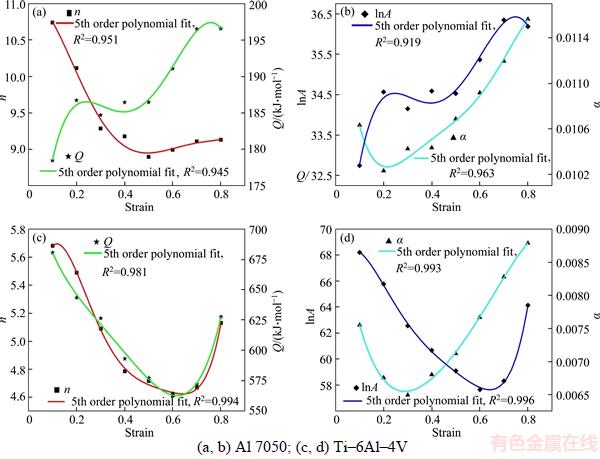
Figure 1 Relationship between coefficient values and strains for:

Figures 2–5 show a comparison between the experimental results and the predicted stress using the two models, including the data at a strain rate of 3 s^–1, which is outside the fit domain. The conclusions are in line with many previous studies, namely significant deviations exist between the experiment and the stresses predicted by the JC model, and the deviations increase dramatically with the amount of strain, which means that the JC model cannot track the trends of the flow curves and the strain softening induced by DRX thus cannot be reflected. It is obvious that the strain– compensated A-type model is more suitable, even for the independent experiment.

The prediction accuracy of constitutive model depends on its form and the data employed in the regression processes. The JC model has a relatively simple form and involves fewer material constants that can be attained using a small batch of experimental data. However, the main problem for this form is the characteristic behavior of work hardening it represents. The gap between the predicted and experimental data widens with the increase of strain due to dynamic softening. Meanwhile, the strain hardening, strain rate hardening, and thermal softening in the model are assumed to be three independent phenomena and can be isolated from each other. The coupled effects of the strain, strain rate, and temperature make the JC model cannot correctly track the flow behavior, particularly at high temperature and high strain rate [16, 25]. The prediction deviation also increases when the deforming conditions are farther from the referential strain rate and temperature.

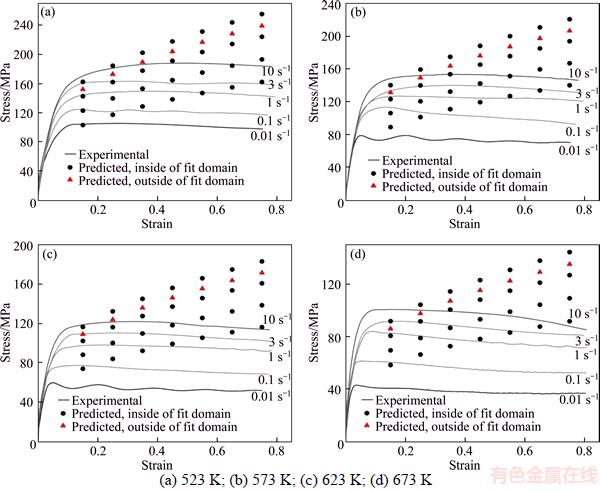
Figure 2 Comparison between experimental and predicted stress of Al 7050 by JC model at different deformation temperatures:

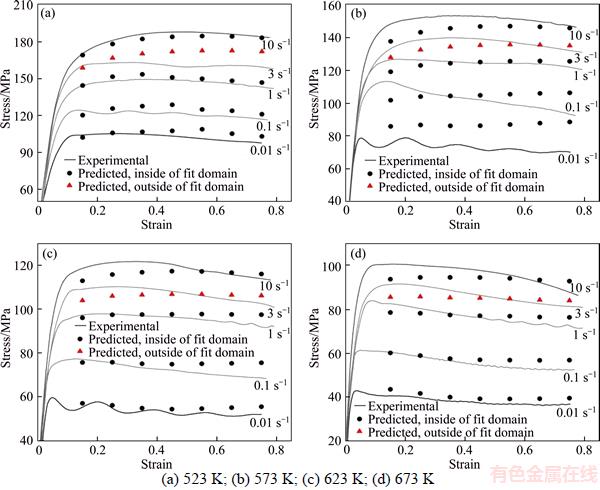
Figure 3 Comparison between experimental and predicted stress of Al 7050 by A-type model at different deformation temperatures:

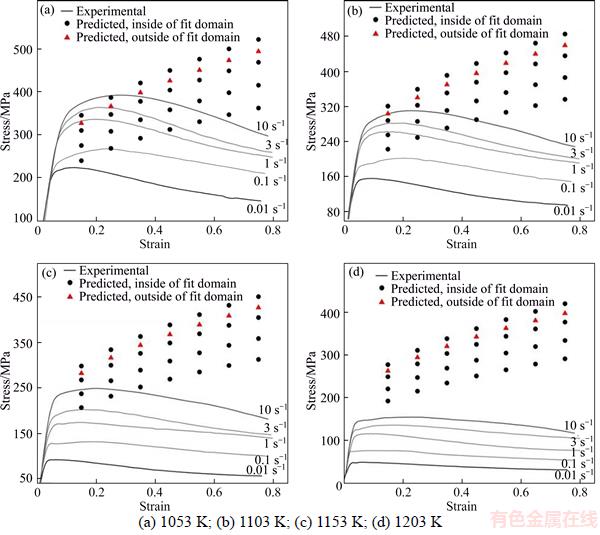
Figure 4 Comparison between experimental and predicted stress of Ti–6Al–4V by JC model at deformation temperatures:

4 FEM simulation of compressive processes utilizing models

In the following, the equations constructed for the two alloys were embedded into the finite element software DEFORM-3D to analyze the thermal compressive courses. The size of the specimens is Φ10 mm×15 mm. The 3D models were meshed with about 20000 to 25000 tetrahedral elements, while the materials were assumed to be rigid viscoplastic. Interface friction was characterized using the shear friction law with a friction factor of 0.3.

4.1 Flow stress

In the uniaxial compressive tests of cylinders, the above experimental flow (the von Mises) stresses can be approximately construed as an average compressive stress σ_z along the axis Z, or simply the average normal stress on the top (or bottom) surface. There are several analytical solutions regarding the normal stress on the surface of the compressed cylinders. For instance, the result by the slab method can be expressed as [32]:

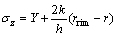                      (11)

whereFor the uniaxial compression of a cylinder, k=Y/2.

Figures 6 and 7 present the comparison of normal stresses on the upper surfaces of the cylinders at strains of 0.15 and 0.75 (height reduction △h of 2.1 mm and 7.9 mm) and strain rate of 3 s^–1 obtained from experiments, FEM simulation using the models and Eq. (11), and the contours of the simulated stress of σ_z inside the samples. It can be found that the stress distributions and the normal stresses on the surface obtained by various methods are different in terms of the magnitude and trend of progression.

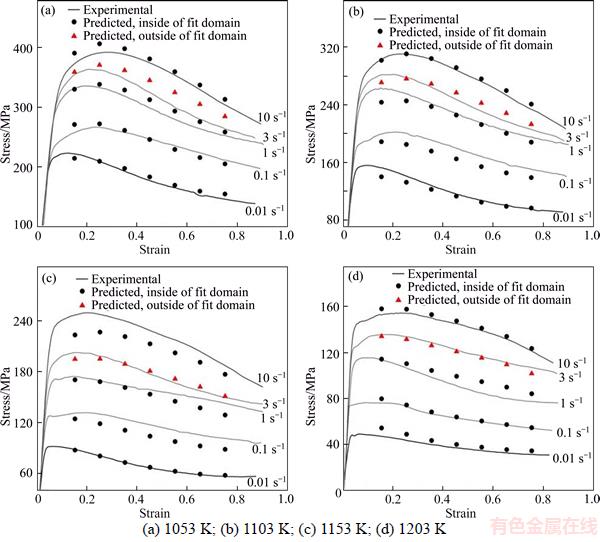
Figure 5 Comparison between experimental and predicted stress of Ti–6Al–4V by A-type model at different deformation temperatures:

Figure 6 Comparison between experimental and theoretical distributions of stress σ_z on top surface and inside of samples at strain of 0.15 and strain rate of 3 s^–1:

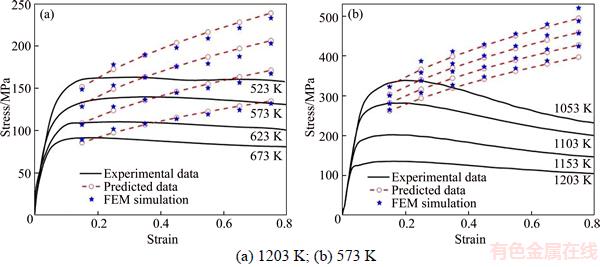
Figure 7 Comparison between experimental and theoretical distributions of stress σ_z on top surface and inside of samples at strain ε of 0.75 and strain rate of 3 s^–1:

As a whole, the stress σ_z simulated with the JC model is larger than those simulated with the A-type model. On the upper surface, normal stresses simulated by the A-type model are closer to the experimental data, while those calculated by the slab method and simulated using the JC model increase significantly with the height reduction (strain). The differences increase with the deformation degree, so the strain softening cannot be properly represented by the JC model as mentioned previously. This situation is consistent with that of the direct calculation, indicating that the numerical simulation is in accord with the analytical calculation in the prediction of stress. Regarding the distributions of stresses, the stress σ_z in the simulation with varying models has a similar distribution mode inside the specimens, and the difference is reduced with the deformation degree. On the upper surface, the results from the numerical simulation are all characterized as low around the center and high at the edge of the specimen, whereas σ_z calculated by the slab method is reduced from the center to the periphery in a linear fashion.

Figures 8 and 9 show the comparison of flow stresses from the experiment, direct calculation, and simulation with the two models at a strain rate of 3 s^–1. The reference strains of the A-type model are 0.15, 0.45, and 0.75. For the numerical simulation, average values of the normal stresses on the top surfaces were used. It can be seen that because of the poor intrinsic prediction ability of the JC model, the gaps between the experimental and simulated results are large. However, for the A-type model only a certain set of coefficients of the reference strain can be input into DEFORM-3D (here it is 0.45), other constants at different strains were not considered in the simulation. Plastic strain influences the deformation resistance via many aspects including the athermal stress, the average activation volume, and the density of mobile dislocations [12]. Under such conditions, it can be observed that the goodness of fit between the predicted stresses from the simulation and direct calculation using the A-type model is not as good as that of the JC model. Furthermore, it can be found in Figure 9 that the deviation among the simulated data using different coefficients in the A-type equation decreases when the temperature increases. The reason could be that the higher the temperature is, the more obvious the linear features of the experimental flow curves for fitting are.

4.2 Overall deformation and strain distribution

Figure 10 shows the experimental and simulation results of the compressed Al 7050 and Ti–6Al–4V specimens. Figure 11 gives a comparison of the experimental and simulated outlines of the cross sections of Al 7050. The deformed workpieces were cut from the axial plane of symmetry. It can be clearly seen that the deformation and strain fields are non-uniform due to the so-called “barreling effect,” which is mostly caused by the friction between the contacting surfaces of the specimen and the anvil. The strain distributions are similar to the results in most of the previous studies on cylinder upsetting [33]. Generally, the uneven strain distribution is characterized by a typical X-shape marks off three domains at varying deformation degrees, namely domains I, II, and III, which represent the regions with small, medium, and large deformation,respectively.

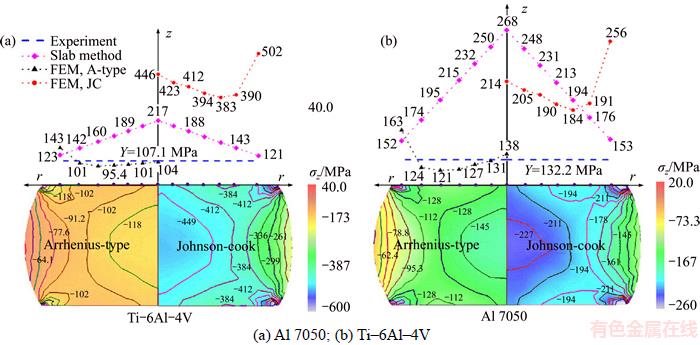
Figure 8 Comparison of experimental, predicted, and simulated flow stresses by JC model at strain rate of 3 s^–1:

Figure 9 Comparison of experimental, predicted, and simulated flow stresses by A-type model at strain rate of 3 s^–1:

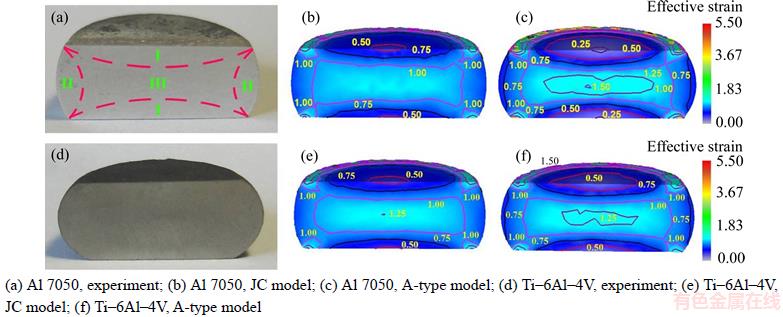
Figure 10 Section view of deformed Al 7050 (at 573 K, 3 s^–1) and Ti–6Al–4V (at 1103 K, 0.1 s^–1) samples at △h=9 mm:

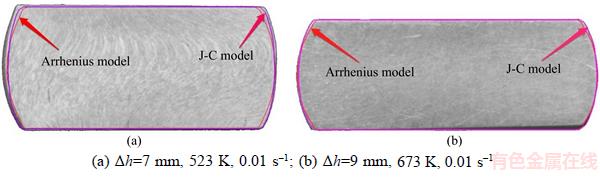
Figure 11 Comparison of cross sections of deformed Al 7050 samples:

In sum, no substantial difference was observed in the strain distributions and in the overall deformations in terms of the outlines of the cross sections (see Figure 11), from the numerical simulation using different models, indicating that in FEM simulation, the influence of constitutive equations on the hot rheology behavior of metals is smaller than that on the flow stress. This phenomenon might be associated with the internal algorithm of the rigid-plastic FEM. Therefore, the plastic flow of material during plastic deformation, together with the deformed geometries, can be properly represented by numerical FEM simulation using these models.

For Al 7050, the simulated and experimental cross-section shapes agree with each other very well. However, it was found that the cross sections of the experimental compressed Ti–6Al–4V samples are quite convex along the transverse direction, meaning the “barreling effect” is more obvious. Generally, this effect is distinct when the friction increases. According to Coulomb’s law, the friction shear force is related to the normal stress on the surface, so the friction on the surfaces of Ti–6Al–4V specimens is larger since the forming loads are bigger. As discussed, stress distributions are different when various constitutive models are utilized, but it does not make much difference with regard to the friction force when a constant friction model is used.

5 Conclusions

This work objectively examined the capabilities of constitutive models, in particular considering the application of FEM simulation. Two models, the Johnson-Cook and Arrhenius-type hyperbolic sine equations, were used to judge the performance regarding the thermal compression of 7050 aluminum and Ti–6Al–4V titanium alloys in a wide range of temperatures and strain rates. The main conclusions are as follows:

1) In the direct prediction of stresses, the strain-compensated A-type model has higher accuracy than the JC model, even for the data outside of the fit domain.

2) The normal stresses on the top surfaces of the samples and the inside stress distributions of σ_z obtained by varying methods are quite different in terms of quantity and progression trends. However, the numerical simulation is in good accord with the analytical calculation in the prediction of stress. As a whole, the results simulated by the A-type model are closer to the experimental data, whereas the JC model has a lower level of accuracy. Stresses from the slab method and simulation using the JC model increase significantly with the height reduction (strain), so the strain softening induced by DRX cannot be perfectly reflected using the JC model.

3) The difference between the strain distributions and overall deformations of the compressed samples in the rigid-plastic FEM simulation using the two models is not obvious, indicating that the influence of constitutive equations on the hot rheology behavior of metals in FEM simulation is relative small. Therefore, plastic flow of the materials during the forming processes can be represented properly, and the deformed geometries of the specimens can be obtained precisely utilizing these models.

4) The A-type model features high prediction accuracy in the analytical calculation and numerical simulation over the entire range of deformation conditions, but the results of direct calculation and simulation are not matched as well as with the JC model if the strain compensation is not considered in the simulation.

Nomenclature

σ

von Mises stress, MPa

ε

Equivalent strain

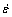
Strain rate, s^–1

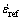
Reference strain rate in JC model, s^–1

K

Yield stress under reference temperature and strain rate

K₁

Coefficient of strain hardening

m

Thermal softening coefficient

A, A₁, A₂

Structural coefficients

α, β

Material constants

E_i

Experimental data, MPa

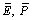
Mean values of E and P

σ_z

Stress component along z-axis, MPa

k

Yield strength in pure shear, MPa

T

Absolute temperature, K

T_melt

Melting temperature, K

T_ref

Referential temperature (usually the lowest temperature in experiment), K

Q

Hot deformation activation energy, kJ/mol

n, n₁

Work-hardening coefficients

C

Coefficient of strain rate hardening

R

Gas constant, 8.314 J/(mol·K)

h

Height of the specimen, mm

Δh

Height reduction of the specimen, mm

τ

Shear stress, MPa

P_i

Predicted value obtained by constitutive equations, MPa

r, r_rim

Radial position; outer radius on the upper surface of the specimen, mm

Y

Initial yield stress, MPa

References

[1] WEN Tong, YUE Yuan-wang, LIU Lan-tao, YU Jian-ming. Evaluation and prediction of hot rheological properties of Ti–6Al–4V in dual-phase region using processing map and artificial neural network [J]. Indian Journal of Engineering & Materials Sciences, 2014, 21(12): 647–656.

[2] Liang R, Khan A S. A critical review of experimental results and constitutive models for BCC and FCC metals over a wide range of strain rates and temperatures [J]. International Journal of Plasticity, 1999, 15(9): 963–980.

[3] Schulze V, Vhringer O. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures [C]// Proceedings of the 7th International Symposium on Ballistics. 1983: 41–47.

[4] Prawoto Y, Fanone M, Shahedi S, Ismail M S, Wan Nik W B. Computational approach using Johnson- Cook model on dual phase steel [J]. Computational Materials Science, 2012, 54(3): 48–55.

[5] Zerilli F J, Armstrong R W. Dislocation- mechanics-based constitutive relations for material dynamics calculations [J]. Journal of Applied Physics, 1987, 61(5): 1816–1825.

[6] Li H Y, Wang X F, Liu J J, Wu Y. A comparative study on modified Johnson Cook, modified Zerilli-Armstrong and Arrhenius-type constitutive models to predict the hot deformation behavior in 28CrMnMoV steel [J]. Materials & Design, 2013, 49(8): 493–501.

[7] Samantaray D, Mandal S, Borah U, Bhaduri A K, Sivaprasad P V. A thermo-viscoplastic constitutive model to predict elevated-temperature flow behaviour in a titanium-modified austenitic stainless steel [J]. Materials Science and Engineering A, 2009, 526(1, 2): 1–6.

[8] Sung J H, Kim J H, Wagoner R H. A plastic constitutive equation incorporating strain, strain-rate, and temperature [J]. International Journal of Plasticity, 2010, 26(12): 1746–1771.

[9] Parsa M H, Ohadi D. A constitutive equation for hot deformation range of 304 stainless steel considering grain sizes [J]. Materials & Design, 2013, 52(12): 412–421.

[10] Kocks U F. Realistic constitutive relations for metal plasticity [J]. Materials Science and Engineering A, 2001, 317(1): 181–187.

[11] Zhou M, Clode M P. Constitutive equations for modelling flow softening due to dynamic recovery and heat generation during plastic deformation [J]. Mechanics of Materials, 1998, 27(2): 63–76.

[12] Cai M C, Niu L S, Ma X F, Shi H J. A constitutive description of the strain rate and temperature effects on the mechanical behavior of materials [J]. Mechanics of Materials, 2010, 42(8): 774–781.

[13] Gupta A K, Krishnamurthy H N, Singh Y, Prasad K M, Singh S K. Development of constitutive models for dynamic strain aging regime in Austenitic stainless steel 304 [J]. Materials & Design, 2013, 45(3): 616–627.

[14] Mirzadeh H, Cabrera J M, Najafizadeh A. Constitutive relationships for hot deformation of austenite [J]. Acta Materialia, 2011, 59(16): 6441–6448.

[15] Lin Y C, Chen M S, Zhong J. Effect of temperature and strain rate on the compressive deformation behavior of 42CrMo steel [J]. Journal of Materials Processing Technology, 2008, 205(1): 308–315.

[16] Lin Y C, Chen X M. A combined Johnson-Cook and Zerilli-Armstrong model for hot compressed typical high-strength alloy steel [J]. Computational Materials Science, 2010, 49(3): 628–633.

[17] Salem A A, Kalidindi S R, Semiatin S L. Strain hardening due to deformation twinning in a-titanium: Constitutive relations and crystal-plasticity modeling [J]. Metallurgical & Materials Transactions A, 2006, 37(1): 259–268.

[18] Gupta A K, Anirudh V K, Singh S K. Constitutive models to predict flow stress in Austenitic Stainless Steel 316 at elevated temperatures [J]. Materials & Design, 2013, 43(1): 410–418.

[19] Rohr I, Nahme H, Thoma K, Anderson C E. Material characterisation and constitutive modelling of a tungsten-sintered alloy for a wide range of strain rates [J]. International Journal of Impact Engineering, 2008, 35(8): 811–819.

[20] Wu H Y, Yang J C, Zhu F J, Wu C T. Hot compressive flow stress modeling of homogenized AZ61 Mg alloy using strain-dependent constitutive equations [J]. Materials Science and Engineering A, 2013, 574(7): 17–24.

[21] Changizian P, Zarei-Hanzaki A, Roostaei A A. The high temperature flow behavior modeling of AZ81 magnesium alloy considering strain effects [J]. Materials & Design, 2012, 39(8): 384–389.

[22] Roy M J, Maijer D M, Dancoine L. Constitutive behavior of as-cast A356 [J]. Materials Science and Engineering A, 2012, 548(6): 195–205.

[23] Sun C, Liu G, Zhang Q, Li R, Wang L. Determination of hot deformation behavior and processing maps of IN 028 alloy using isothermal hot compression test [J]. Materials Science and Engineering A, 2014, 595(2): 92–98.

[24] Wang L, Liu F, Zuo Q, Chen C F. Prediction of flow stress for N08028 alloy under hot working conditions [J]. Materials & Design, 2013, 47(5): 737–745.

[25] Samantaray D, Mandal S, Bhaduri A K. A comparative study on Johnson-Cook, modified Zerilli- Armstrong and Arrhenius-type constitutive models to predict elevated temperature flow behaviour in modified 9Cr-1Mo steel [J]. Computational Materials Science, 2009, 47(2): 568–576.

[26] He A, Xie G, Zhang H, Wang X. A comparative study on Johnson-Cook, modified Johnson-Cook and Arrhenius-type constitutive models to predict the high temperature flow stress in 20CrMo alloy steel [J]. Materials & Design, 2013, 52(12): 677–685.

[27] Ji G, Li F, Li Q, Li H, Li Z. A comparative study on Arrhenius-type constitutive model and artificial neural network model to predict high-temperature deformation behaviour in Aermet100 steel [J]. Materials Science and Engineering A, 2011, 528(13, 14): 4774–4782.

[28] Li H Y, Wang X F, Wei D D, Hu J D, Li Y H. A comparative study on modified Zerilli-Armstrong, Arrhenius-type and artificial neural network models to predict high-temperature deformation behavior in T24 steel [J]. Materials Science and Engineering A, 2012, 536(2): 216–222.

[29] Gupta A K, Singh S K, Reddy S, Hariharan G. Prediction of flow stress in dynamic strain aging regime of austenitic stainless steel 316 using artificial neural network [J]. Materials & Design, 2012, 35(3): 589–595.

[30] Mandal S, Rakesh V, Sivaprasad P V, Venugopal S, Kasiviswanathan K V. Constitutive equations to predict high temperature flow stress in a Ti-modified austenitic stainless steel [J]. Materials Science and Engineering A, 2009, 500(1, 2): 114–121.

[31] Tian Y, Huang L, Ma H, Li J. Establishment and comparison of four constitutive models of 5A02 aluminium alloy in high-velocity forming process [J]. Materials & Design, 2014, 54(2): 587–597.

[32] Hosford W F, Caddell R M. Metal forming- Mechanics and Metallurgy [M]. New York: Cambridge University Press, 2007.

[33] Lin Y C, Chen M S, Zhong J. Numerical simulation for stress/strain distribution and microstructural evolution in 42CrMo steel during hot upsetting process [J]. Computational Materials Science, 2008, 43(4): 1117–1122.

(Edited by FANG Jing-hua)

中文导读

考虑有限元应用的本构模型预测能力评估

摘要：本构模型在金属塑性成形数值模拟中扮演着重要角色，然而其对计算的影响仍不明确。本文基于Al 7050和Ti–6Al–4V合金的等温压缩实验应力–应变曲线，对Johnson-Cook (JC)以及Arrhenius-type (A-type) 双曲正弦模型进行了拟合并得到表达式；将应用2个方程直接预测的流动应力与实验结果进行比较，同时利用刚塑性有限元数值方法对热压缩过程进行模拟，发现对于实验数据的直接预测，A-type模型的预测精度高于JC模型的，对拟合数据以外的实验数据也一样。从数值模拟结果来看，利用A-type模型的计算结果与实验更加吻合，但吻合程度受拟合所采用参考参数的影响；从模拟得到的整体变形和应变分布来看，利用2种模型的结果差别不大。

关键词：本构模型；金属成形；数值模拟；性能；等温压缩

Foundation item: Project(2012ZX04010-81) supported by the National Key Technology R&D Program of China; Project (51575066) supported by the National Natural Science Foundation of China

Received date: 2016-09-22; Accepted date: 2016-12-14

Corresponding author: WEN Tong, PhD, Professor; Tel: +86–13018363383; E-mail: wentong@cqu.edu.cn; ORCID: 0000-0003-3266- 2212