­­First-principles calculations of lattice stability of technetium and rhenium

TAO Hui-jin(陶辉锦)^{1, 2, 3}, CHEN Wei-min(陈伟民)^{1, 2}, ZHOU Wen(周 文)⁴, WANG He-nan(王赫男)^{1, 2}

1. School of Materials Science and Engineering, Central South University, Changsha 410083, China;

2. Key Laboratory of Nonferrous Materials Science and Engineering, Ministry of Education,

Central South University, Changsha 410083, China;

3. School of Metallurgical Science and Engineering, Central South University, Changsha 410083, China;

4. School of Energy Science and Engineering, Central South University, Changsha 410083, China

Received 10 August 2009; accepted 15 September 2009

Abstract: Lattice constants, total energies and densities of state of technetium(Tc) and rhenium(Re) with different crystalline structures were calculated with the GGA+PBE function, ultra-soft pseudo-potential and plane wave method in first-principles. The results were compared with those of projector augmented wave(PAW) method in first-principles and experimental data. The lattice stability results prove that HCP phase is the most stable phase, which agrees well with those of PAW method in first-principles and CALPHAD method. Further analyses of densities of state also give the same result of lattice stability for HCP-, FCC-, BCC-Tc and Re. Analyses of atomic populations show that the lattice stability of technetium and rhenium is probably related to the electrons in p and d state.

Key words: technetium; rhenium; lattice stability; first principles

1 Introduction

The SGTE database of pure elements[1] has established the lattice stability parameters and expressions of Gibbs energy of different structures for 78 kinds of elements at 298.15 K. Compared with the CALPHAD methods based on fitting and extrapolation of experimental data, first-principles methods can be applied to the calculations of total energy, electronic structure and other physical properties as cohesive energy and heat of formation of metals and alloys[2-4]. It is much important that the physical reasons of lattice stability of metals and alloys can be expected to be further understood by calculations and discussion of the total energy[5-7]. Specifically, the calculations of lattice stabilities of materials including transition metals and other simple metals have been discussed systematically[8].

To find the physical reason of lattice stability at the level of electronic structure, the difference between various methods used in first-principles and the difference between first-principles and CALPHAD methods, in this work, the total energies, lattice constants and densities of state of elemental technetium(Tc) and rhenium(Re) are calculated with pseudo-potential plane wave method[9] and the general gradient approximation(GGA) in first- principles[10]. All the methods, including CALPHAD method, the pseudo-potential plane wave method and the projector augment wave method in first-principles are compared and discussed. This work will provide meaningful data for the phase diagram calculations of alloys containing technetium(Tc) and rhenium(Re) and physical understanding of the lattice stability of Tc and Re.

2 Calculation

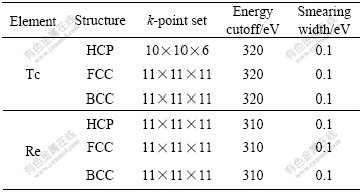
Lattice constants, total energies and densities of state of HCP-, FCC-, BCC-Tc and Re have been calculated with the pseudo-potential plane wave method in first principles. The calculations are performed in CASTEP program with ultra-soft pseudo-potential and GGA+PBE functional. Geometric optimization of lattice parameters is performed in original cell. The total energyand other properties are calculated individually to avoid the influence of Pulay stress[11] after series of geometric optimizations with medium, fine and ultrafine qualities, respectively. At the same time, the limited temperature smearing Gaussian method has been adopted to accelerate the convergence of integration at Brilluin zone [12].

Table 1 Crystalline structure, k-point set, energy cutoff and smearing width of Tc and Re

3 Results

3.1 Lattice constants and atomic volumes

Table 2 lists the results of lattice constants and atomic volume after geometric optimization.

3.2 Cohesive energies

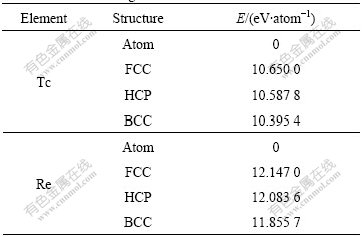
Table 3 lists the results of cohesive energies[13].

Table 2 Lattice constants and atomic volumes of HCP-, FCC-, BCC-Tc and Re

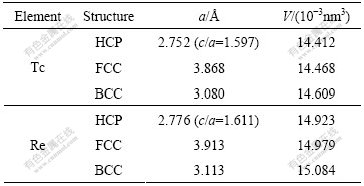
Table 3 Cohesive energies of Tc and Re

3.3 Density of state and atomic population

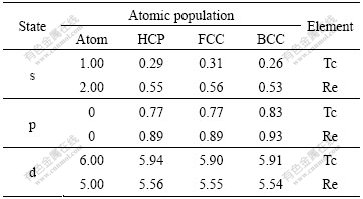
The difference of electronic structures is the intrinsic reason of lattice stability. The electronic structures of HCP-, FCC-, BCC-Tc and Re are calculated. Figs.1, 2 and 3 show the total density of states, partial density of s state electrons, partial density of p state electrons and partial density of d state electrons of HCP-, FCC-, BCC-Tc and Re, respectively. The atomic populations are presented in Table 4 to analyze the density of state quantitatively.

The electronic configurations of atomic Tc and Re on the ground state are [Kr]4d⁶5s¹ and [Xe] 4f¹⁴5d⁵6s², and the total valence electron number is 7. When these atoms are condensed into crystals, the chemical bonds and energy bands form. Table 4 presents the changes.

Table 4 Atomic population of HCP-, FCC-, BCC-Tc and Re

4 Analyses and discussion

4.1 Lattice stability parameters

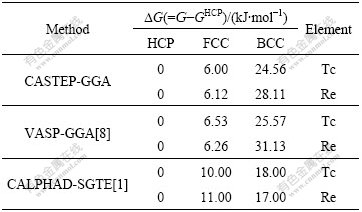
The lattice stability parameters are in fact the relative Gibbs energy G, which describes the relative stability of phases. For technetium and rhenium, the lattice stability parameters are the energy difference (G-G^HCP) of FCC and BCC phases relative to HCP phase, which is dependent on temperature. At the same time, in this work only the case at 0 K is discussed. So, there is

G-G^HCP=H-H^HCP≈U-U^HCP                    (1)

where H is the enthalpy, and U is the internal energy. The results of internal energy U-U^HCP calculated in first principles can be compared with the Gibbs energy G-G^HCP in SGTE database with CALPHAD method. The difference between CALPHAD and first-principles methods and the difference between first-principles methods themselves can be compared and discussed at the same time. The results are listed in Table 5.

It is shown in Table 5 that the two theoretical results of lattice stability of technetium and rhenium are the same, i.e., ?G^BCC-HCP＞?G^FCC-HCP＞0. And HCP phase is determined to be the most stable phase by all the three methods, agreeing well with the experimental facts. The relationship between lattice stability and electronic structure then can be further discussed.

Fig.1 Total density (a), partial density of s state (b), partial density of p state (c), and partial density of d state (d) of HCP-Tc and Re

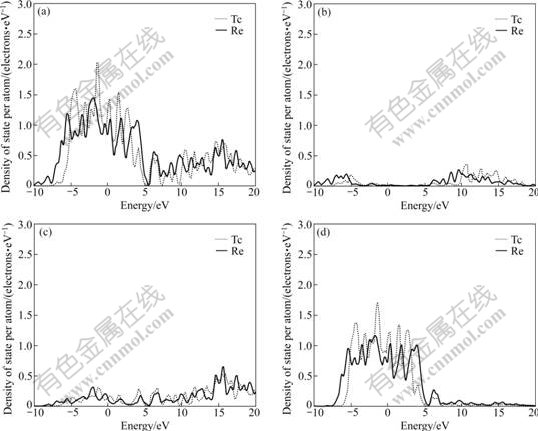
Fig.2 Total density (a), partial density of s state (b), partial density of p state (c), and partial density of d state (d) of FCC-Tc and Re

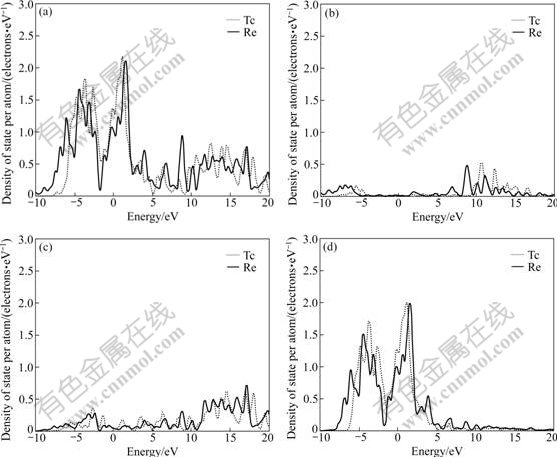
Fig.3 Total density (a), partial density of s state (b), partial density of p state (c), and partial density of d state (d) of BCC-Tc and Re

Table 5 Lattice stability parameters of HCP-, FCC-, BCC-Tc and Re

4.2 Total energy

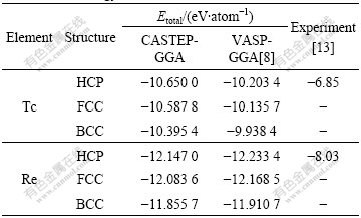
Total energy is a generalized concept, and cohesive energy is the energy of condensed matter relative to free atom[13]. For research convenience, the free atom state is chosen as the reference state to calculate the differences of total energies between different structures, as listed in Table 6.

It is known that there are some differences between the theoretical results and experimental values. The large discrepancies between the first-principles calculations and the SGTE data may be partly attributed to the difference in temperature condition, which may be reduced through the effect of alloying elements[8].

Table 6 Total energy of HCP-, FCC-, BCC-Tc and Re

4.3 Densities of state and atomic populations

It is known from the comparison of total density of state, partial density of s state electrons, partial density of p state electrons and partial density of d state electrons in Figs.1, 2 and 3 that the Fermi energies of HCP-Tc and Re lie in the valley between two peaks of DOS with the obvious characteristic of stable phase, and those of FCC, BCC-Tc and Re lie in the plat of peaks of DOS with the obvious characteristic of metastable and unstable phase, which agree well with the total energy calculations.

It is known from Table 4 that BCC phase has the most electrons in p state and HCP phase has the most electrons in d state with the variation of crystalline structures. This shows that the lattice stability of technetium and rhenium is probably related to the electrons in p and d state.

5 Conclusions

1) The two lattice stability results by both pseudo- potential plane wave method and projector augmented wave method in first-principles for technetium and rhenium are all ?G^BCC-HCP＞?G^FCC-HCP＞0, where HCP phase is determined to be the most stable phase.

2) There are some differences between the theoretical results and experimental values in total energies and large discrepancies between the first- principles calculations and the SGTE data, which may partly be reduced through the effect of alloying elements.

3) The Fermi energies of HCP-Tc and HCP-Re lie in the valley between two peaks of DOS with the obvious characteristic of stable phase, and those of FCC- and BCC-Tc and Re lie in the plat of peaks of DOS with the obvious characteristic of metastable, which agree well with the total energy calculations.

4) The lattice stability of technetium and rhenium probably depends on the electrons in p and d state.

References

[1] DINSDALE A T. SGTE data for pure elements [J]. CALPHAD, 1991, 15(4): 317-425.

[2] KISSAVOS A E, SHALLCROSS S, KAUFMAN L, GR?N?S O, RUBAN A V, ABRIKOSOV I A. Thermodynamics of ordered and disordered phases in the binary Mo-Ru system [J]. Physical Review B, 2007, 75(18): 184203-184210.

[3] BRUTTI S, NGUYEN-MANH D, PETTIFOR D G. Lattice stability of Ca, Sr and Yb disilicides [J]. Intermetallics, 2006, 14: 1472-1486.

[4] GHOSH G, van de WALLE A, ASTA M. First-principles calculations of the structural and thermodynamic properties of bcc, fcc and hcp solid solutions in the Al-TM (TM = Ti, Zr and Hf) systems: A comparison of cluster expansion and supercell methods [J]. Acta Materialia, 2008, 56: 3202-3221.

[5] ASKER C, BELONOSHKO A B, MIKHAYLUSHKIN A S, ABRIKOSOV A S. First-principles solution to the problem of Mo lattice stability [J]. Physical Review B, 2008, 77(22): 220102-220105.

[6] GHOSH G, DELSANTE S, BORZONE G, ASTA M, FERRO R. Phase stability and cohesive properties of Ti-Zn intermetallics: First-principles calculations and experimental results [J]. Acta Materialia, 2006, 54: 4977-4997.

[7] GAO M C, ROLLETT A D, WIDOM M. Lattice stability of aluminum-rare earth binary systems: A first-principles approach [J]. Physical Review B, 2008, 75(17): 174120-174135.

[8] WANG Y, CURTAROLO S, JIANG C, LIU Z K. Ab initio lattice stability in comparison with CALPHAD lattice stability [J]. CALPHAD, 2004, 28(1): 79-90.

[9] MILMAN V, WINKLER B, WHITE J A, PICKARD C J, PAYNE M C, AKHMATSKAYA E V, NOBES R H. Electronic structure, properties and phase stability of inorganic crystals: A pseudopotential plane-wave study [J]. International Journal of Quantum Chemistry, 2000, 77(5): 895-910.

[10] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Physical Review Letters, 1996, 77(18): 3865-3868.

[11] PULAY P. Convergence acceleration of iterative sequences: The case of SCF iteration [J]. Chemical Physical Letters, 1980, 73(2): 393-398.

[12] METHFESSEL M, PAXTON A T. High-precision sampling for Brillouin-zone integration in metals [J]. Physical Review B, 1989, 40(6): 3616-3621.

[13] KITTEL C. Solid state physics [M]. New York: John Wiley and Sons Inc, 1976: 55.

 (Edited by YANG Bing)

Foundation item: Project(20070533118) supported by the Doctoral Discipline Foundation of the Ministry of Education of China; Project(50871124) supported by the National Natural Science Foundation of China; Project supported by the Postdoctoral Foundation of Central South University, China

Corresponding author: TAO Hui-jin; Tel/Fax: +86-731-88876992; E-mail: thj@mail.csu.edu.cn