J. Cent. South Univ. Technol. (2011) 18: 593-599
DOI: 10.1007/s11771-011-0736-0
Kineto-static analysis of a novel high-speed parallel manipulator with rigid-flexible coupled links
SUN Tao(孙涛), SONG Yi-min(宋轶民), YAN Kai(阎凯)
School of Mechanical Engineering, Tianjin University, Tianjin 300072, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: A novel high-speed parallel kinematic machine (PKM) named Delta-S parallel manipulator is proposed, which consists of a fixed base connected to a moving platform through three limbs with identical topology. Each limb is composed of one driving arm and one follower arm, herein, the latter includes two strings and one middle rod, all located in a same plane. Compared with similar manipulators with uniform parameters, the novel and unique topology as well as the addition of two strings of Delta-S manipulator can remove the clearance of the spherical joints, reduce the inertial load of components further, improve the positioning accuracy and dynamic performance, and so on. In order to formulate the kineto-static model of Delta-S manipulator, the kineto-static analyses and models of the driving arm, the generalized follower and the moving platform can be carried out by the D’ALEMBERT principle. For the sake of obtaining the force analytic results of strings, the deformation compatibility condition of strings and the middle rod are determined. Furthermore, in virtue of the assumption of small deformation and the linear superposition principle, the minimal pre-tightening force of the strings is calculated. The main results include that the loads of the strings and the middle rod must be larger than “zero” and the pre-tightening force over the workspace must be larger than the minimal pre-tightening force at any time within the workspace, which lay the foundation for the dynamic analysis and the prototype manufacture of the Delta-S manipulator.
Key words: parallel kinematic machines (PKMs); Delta-S manipulator; kineto-static analysis; deformation compatibility condition; pre-tightening force
1 Introduction
The parallel kinematic machines (PKMs) have attracted much attention because of many merits and then have experienced six-degree-of-freedom (6-DOF) PKMs [1-3] and the limited-DOF PKMs including 5-DOF, 4-DOF, 3-DOF and 2-DOF PKMs [4-8]. However, the invention and application of Delta robot [9] modify the people’s conventional comprehension on general PKMs and it may be a breakthrough of the high-speed limited-DOF PKMs. The application of the light-weight and slender limbs in Delta robot gain the high velocity and acceleration of the end-effector, which can be applied in the production line of Pick-and-Place and advances the production efficiency availably, and then the more important thing is that the supply of creative ideas for some similar mechanisms such as HEXA robot [10], UWA Delta robot [11], Deltabot [12-13], and Diamond [14-15].
However, many rods in the limbs of Delta robot or Delta-like mechanisms may lead to the occurrence of large inertia and intense impact in the high-speed motions, which may influence the precision and stability of the mechanism systems. In order to settle these related problems, a novel high-speed PKM with rigid-flexible coupled links named Delta-S (S stands for string) manipulator [16] is proposed in this work. Compared with Delta robot, the follower arm of Delta-S consists of two strings instead of the two rods in the Delta robot and a middle rod is added between the two strings. The application of the strings can decrease the inertia and the impact effectively. Moreover, the precision and the stability of Delta-S parallel manipulator may be improved accordingly.
Compared with the studies of Delta robot, the string research in the Delta-S is a more difficult and challenging problem. The analysis of the string is replaced by that of the cable in lots of references based on their similar characteristics. Back to 17th centuries, GALILEO, BERNOULLI and POISSON took their own contributions to string researches regarding the foundational theory, followed by the formulation of the numerical solution for the planar cable by O’BRIEN [17], which accelerated the cable developments greatly. Besides, the stiffness problem of the cable was preceded by IRVINE [18], RAID [19], RUSSELL and LARDNER [20] and others.
Based on the researches of the cable and the string, a novel high-speed PKM with rigid-flexible coupled links called “Delta-S manipulator” is presented in this work, composed of a fixed base, a moving platform and three identical limbs. The topology of each limb includes one driving arm and one follower arm; however, two strings and one middle rod constitute the follower arm and locate in one same plane. The kineto-static analyses of the driving arm, the follower arm and the moving platform may be executed in the first place, respectively, and then the kineto-static model of Delta-S parallel manipulator is formulated based on the D’ALEMBERT principle. Furthermore, the minimal pre-tightening force of the two strings in the follower arm is calculated after its deformation compatibility condition is determined. Finally, one example is provided to prove the validity of the method mentioned-above.
2 Description and definition
As demonstrated in Fig.1, the Delta-S parallel manipulator is composed of a fixed base, a moving platform and three limbs with identical topology and layout. Each limb includes one driving arm BiCi and one follower arm CiAi. The former joins the fixed base with a revolute joint (R joint), and the follower containing two strings and one middle rod connects the driving arm and the moving platform all with spherical joints (S joint).
Without the loss of generality, the planes of the fixed base and moving platform are assumed as two equilateral triangles ΔB1B2B3 and ΔA1A2A3 whose circumradius are nominated as rb and ra. A global coordinate frame designated as the O-xyz frame is fixed at the center of the fixed base with z-axis pointing vertically upwards and y-axis pointing to the point B3, while a moving coordinate frame O′-x′y′z′ is assigned to the center of the moving platform, whose three axes are parallel to those of the frame O-xyz.
Therefore, the closed-form equation may be obtained as
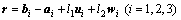 (1)
(1)
where r, bi and ai denote the position vectors of point O′, Bi and Ai in frame O-xyz, respectively. l1 and l2 represent the lengths of the driving arm and the middle rod. Ui and wi are the unit vectors of the i-th driving arm and the i-th middle rod.
It is noteworthy that the similarity of the topology between the Delta-S manipulator and the Delta robot yields the homogeny of the inverse problems, and then the related parameter values of Delta-S manipulator can be obtained easily according to the inverse problem analysis of Delta robot, such as the unit vector of the axis of R joint vi, the angle φi between wi and (vi×ui), the rotating angle θi, the acceleration and angular acceleration 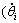 and
and 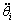 as their notation) of the driving arm, the centric acceleration vector aui of the driving arm, the angular velocity and angular acceleration vector of the follower arm expressed by ωwi and
as their notation) of the driving arm, the centric acceleration vector aui of the driving arm, the angular velocity and angular acceleration vector of the follower arm expressed by ωwi and 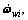 the centric velocity vector and the centric acceleration of the follower arm denoted by vwi and awi, respectively.
the centric velocity vector and the centric acceleration of the follower arm denoted by vwi and awi, respectively.
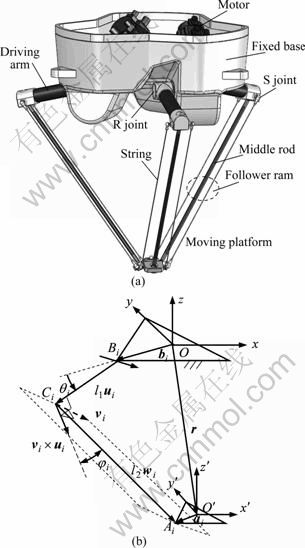
Fig.1 Virtual prototype (a) and schematic diagram (b) of Delta-S manipulator
3 Kineto-static analysis of Delta-S
Due to the little mass of the string, its gravity and inertial force can be ignored, and then the direction of the remaining force applied at the string may be only considered along its axis. Based on these hypotheses, the follower arm is similar to the parallelogram and can be regarded as generalized follower arm. Each generalized follower arm exerts constraint force on both the moving platform and the driving arm through the S joints of the middle rod, and the forces can be nominated as F s1 i and -F s2 i, respectively. In addition, the different axial forces applied on the string lead to the occurrence of the constraint couples exerting on the moving platform and the driving arm, and the couples may be expressed by Mi and -Mi, whose directions are orthogonal to the follower arm planes. Furthermore, the kineto-static analyses of the driving arm, the follower arm and the moving platform can be preceded as follows.
3.1 Driving arm
Figure 2(a) shows the kineto-static model of the driving arm. -F1 i is defined as the constraint force of the driving arm exerted by the fixed base. According to the force relationship, the kineto-static equation of the driving arm may be formulated as
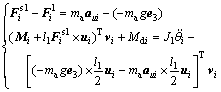 (2)
(2)
where F s1 i=[F s1 ix F s1 iy F s1 iz]T, F1 i=[F1 ix F1 iy F1 iz]T, Mi=Mini, ni=wi×vi and e3=[0 0 1]T. J1 denotes the rotary inertia of the driving arm about its axis and Mdi represents its trimming moment with the direction along vi. ma is the mass of the driving arm and g is the acceleration of gravity.

Fig.2 Kineto-static model of driving arm (a), follower arm (b) and moving platform (c)
Expressing Eq.(2) in matrix form yields
 (3)
(3)
where
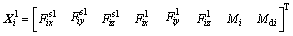
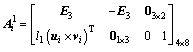
E3=diag(1 1 1)
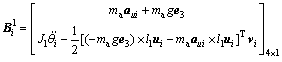
3.2 Follower arm
As shown in Fig.2(b), after ignoring the mass of the string, the forces exerting on the generalized follower arm only include the gravity and inertia force of the middle rod and the constraint forces, -F s1 i and F s2 i. A body-fixed coordinate frame designated as Si-x″y″z″ frame is fixed at the centroid Si of the middle rod with z″-axis along wi and y″-axis parallel to ni. Then, the kineto-static equation of the generalized follower arm may be formulated as
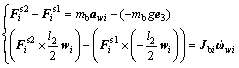 (4)
(4)
where mb is the mass of the middle rod, Jbi denotes the inertia tensor of the middle rod with respect to the frame O-xyz.
Additionally, Fig.1 demonstrates that the inertia tensor of the middle rod about z″-axis is zero, and then Eq.(4) can be rewritten as
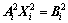 (5)
(5)
where
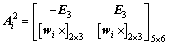
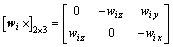
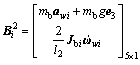
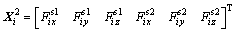
3.3 Moving platform
Figure 2(c) demonstrates the force relationship of the moving platform. After assuming the external force F and the couple M applied at the moving platform, the kineto-static equation of the moving platform can be obtained:
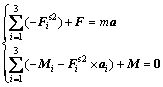 (6)
(6)
where m denotes the mass of the moving platform and ai is the acceleration vector of the centroid for the moving platform.
Rewriting Eq.(6) into matrix leads to
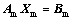 (7)
(7)
where
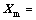
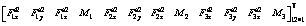
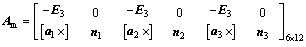
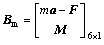
3.4 Kineto-static equation of Delta-S
According to the force analysis of the driving arm, the follower arm and the moving platform, the kineto-static equation of Delta-S manipulator can be written as
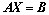 (8)
(8)
where
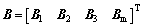
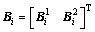
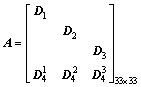
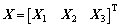
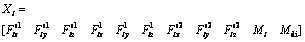

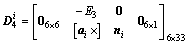
Due to the non-singularity of matrix A, the unknown variables can be solved by
 (9)
(9)
Therefore, the kineto-static model of Delta-S manipulator is formulated according to the D’ALEMBERT principle, and then the force states and their parameter values can be calculated easily.
4 Pre-tightening force analysis of string
As mentioned above, the existence of the two strings in the Delta-S manipulator is used for keeping the follower arm as a parallelogram mechanism and then possessing three translational degrees through its workspace. Therefore, the pre-tightening force analysis is most important for designing the Delta-S prototype. In this section, it is noted that the tensile force is positive, the pressure is negative, the couple is positive along the counter-clockwise and vice versa.
4.1 Initial stage of generalized follower arm
When assembling the Delta-S manipulator, the exertion of the pre-tightening force leads to the fact that the initial stage of the string is actually an equilibrium state, and the static equation of the follower arm may be formulated as
 (10)
(10)
where E0 and E1 denote the elastic moduli of the string and the middle rod, respectively; l0 and L0 represent the unstretched lengths of the string and the middle rod, respectively; l is the length of the string or the middle rod in the equilibrium state; T0 denotes the pre-tightening force of the string and Tg is the initial pressure of the middle rod; A0 and Ag represent the cross sectional areas of the string and the middle rod, respectively.
4.2 Work stage of generalized follower arm
4.2.1 Equivalent constraint force
According to kineto-static analysis of the Delta-S manipulator, forces the F s1 i and F s2 i can be obtained through solving equations. The equivalent forces of both ends of generalized follower arm designated as F s1 wi and F s2 wi are the components of F s1 i and F s2 i along the middle rod axis. However, the forces F s1 wi and F s2 wi must be selected as their maximal values for guaranteeing the validity of the two strings in Delta-S manipulator, and then one can define Pi as Pi=max(F s1 wi F s2 wi).
As shown in Fig.3, the string and the middle rod need extra deformations Δlij' for balancing Pi, where j denotes the j-th (j=1-2) string and j-th (j=3) middle rod. Furthermore, the elastic deformation compatibility equation and the force equation may be expressed as
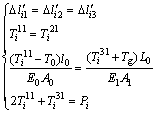 (11)
(11)
where T j1 i denotes the internal force of the string and the middle rod because of the exertion of Pi.
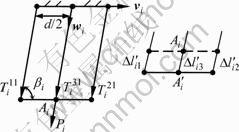
Fig.3 Equivalent constraint force model
4.2.2 Equivalent constraint moment
Similar to the equivalent constraint force analysis of the generalized follower arm, its equivalent constraint moment analysis can be obtained easily, as demonstrated in Fig.4. The elastic deformation compatibility equation leads to
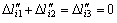 (12)
(12)
and then the moment equation may be formulated as
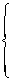
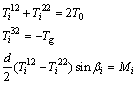 (13)
(13)
where 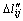 denotes the extra deformation of the string and the middle rod with respect to initial stage, and T j2 i denotes the internal force of the string and the middle rod because of the exertion of Mi.
denotes the extra deformation of the string and the middle rod with respect to initial stage, and T j2 i denotes the internal force of the string and the middle rod because of the exertion of Mi.

Fig.4 Equivalent constraint moment model
4.2.3 Pre-tightening force definition and stability
For balancing Pi and Mi, the axial forces of the string and the middle rod can be calculated based on the linear superposition principle:
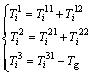 (14)
(14)
where  denotes the axial force of the string and the middle rod. Then,
denotes the axial force of the string and the middle rod. Then,  may be calculated easily from Eqs.(10)-(14).
may be calculated easily from Eqs.(10)-(14).
Based on the discussion mentioned above, the string can only be applied by the tensile force, and then the conditions must be satisfied in order to make the Delta-S manipulator possess three translational DoFs:
T0>0 and 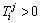 (i=1-3, j=1-2) (15)
(i=1-3, j=1-2) (15)
Under different working conditions, the value of T0 must be larger than the maximal value of T j i, i.e.
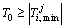 (16)
(16)
Besides defining the minimal pre-tightening force of the string, the stability of the middle rod also needs to be analyzed extensively, and then its stability condition is
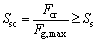 (17)
(17)
where Ssc and Ss (2.5-4) denote calculative and allowable safety coefficients, respectively; Fg,max and Fcr represent the maximal axial and the ultimate loads of the middle rod, respectively.
5 Simulations
As shown in Fig.5, the end-effector trace of Delta-S manipulator, (P1?P2?P3?P4?P5?P6) is demonstrated; besides, the workspace Wt of Delta-S manipulator is given with its radius of R and height of h. H denotes the distance from the fixed base to the upper bound of Wt, and γ denotes the angle between the working plane of the manipulator and x-axis.
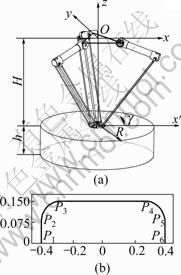
Fig.5 Workspace (a) and path (b) of Delta-S manipulator
Tables 1 and 2 provide the related parameters of the Delta-S manipulator, where d and d0 denote the distance between the two strings and the diameter of the string, respectively, D1 and D2 represent the external and internal diameter of the middle rod, respectively, and sP represents the proportional limit of the middle rod. Furthermore, the manipulator can move under the loads including F=[0 0 -mg] and M=[0 0 0]. Then, the motion regularity of the end-effector is given as
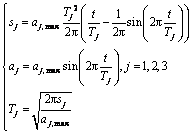 (18)
(18)
where j=1, denotes the section of P1?P3, j=2, is that of P2?P5, and j=3, is that of P4?P6; Tj represents the kinetic time of j-th section, while aj,max is the maximal acceleration of j-th section and its values is given to be 50 m/s2.
Table 1 Parameters of Delta-S manipulator

Table 2 Parameters of components

After assuming the pre-tightening force T0=0, 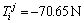 can be calculated easily; however, Eq.(15) tells that the value of pre-tightening force T0 must be adjusted and can be selected to be 80 N. Therefore, the force state of the i-th string can be found in Figs.6(a)-(c). It is indicated that the adjusted pre-tightening force is appropriate and the forces of the two strings in the same limb are symmetrical about the pre-tightening force. At the same time, the stability analysis of the middle rods in the limbs is carried out. Fg,max=40.6 N and Ssc=118>>Ss declare that the middle rod is very stable.
can be calculated easily; however, Eq.(15) tells that the value of pre-tightening force T0 must be adjusted and can be selected to be 80 N. Therefore, the force state of the i-th string can be found in Figs.6(a)-(c). It is indicated that the adjusted pre-tightening force is appropriate and the forces of the two strings in the same limb are symmetrical about the pre-tightening force. At the same time, the stability analysis of the middle rods in the limbs is carried out. Fg,max=40.6 N and Ssc=118>>Ss declare that the middle rod is very stable.
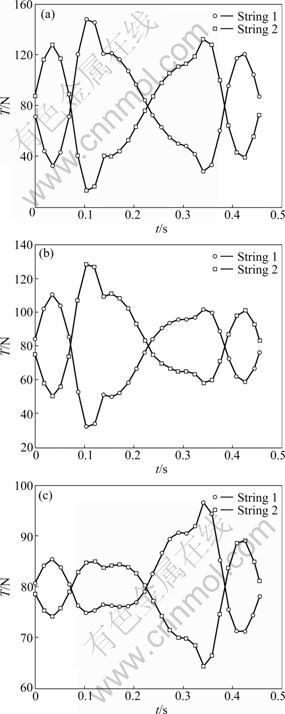
Fig.6 Force states of two strings (string 1 and 2) in three limbs: (a) 1st limb; (b) 2nd limb; (c) 3rd limb
6 Conclusions
1) Compared with the topology of Delta robot, the topology of Delta-S manipulator possesses two strings in each limb, and the two strings and one middle rod constitute the follower arm, which can decrease the inertia and the impact of Delta-S manipulator effectively, and can improve the precision and stability accordingly.
2) After the kineto-static analyses of the driving arm, the generalized follower arm and the moving platform, the kineto-static model of Delta-S manipulator may be formulated based on the D’ALEMBERT principle. Finally, the force states and its parameter values of three limbs are obtained.
3) Based on the kineto-static model of Delta-S manipulator, the deformation compatibility conditions of the string and the middle rod are formulated. Furthermore, the minimal pre-tightening force of the string can be calculated, as well as the inertial force states of the initial stage and the work stage, which lay the foundation for the dynamic analysis and the virtual prototype of Delta-S parallel manipulator.
References
[1] TLUSTY J, ZIEGERT J, RIDGEWAY S. Fundamental comparison of the use of serial and parallel kinematics for machine tools [J]. CIRP Annals-Manufacturing Technology, 2002, 48(1): 351-356.
[2] WECK M, STAIMER D. Parallel kinematic machine tools—current state and future potentials [J]. CIRP Annals-Manufacturing Technology, 2002, 51(2): 671-683.
[3] CORBEL D, COMPANY O, PIERROT F. Optimal design of a 6-dof parallel measurement mechanism integrated in a 3-dof parallel machine-tool [C]// Proceedings of 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems. Nice, France: IEEE Press, 2008: 1970-1976.
[4] ZHU S J, HUANG Z, ZHAO M Y. Singularity analysis for six practicable 5-DoF fully-symmetrical parallel manipulators [J]. Mechanism and Machine Theory, 2009, 44: 710-725.
[5] LU Yi, SHI Yan, HUANG Zhen, YU Jian-ping, LI Shi-hua, TIAN Xing-bin. Kinematics/statics of a 4-DOF over-constrained parallel manipulator with 3 legs [J]. Mechanism and Machine Theory, 2009, 44: 1497-4506.
[6] SUN Tao, SONG Yi-min, LI Yong-gang, ZHANG Jun. Stiffness estimation for the 4-DOF hybrid module of a novel reconfigurable robot [C]// Proceedings of 2009 ASME/IFToMM International Conference on Reconfigurable Mechanisms and Robots. London, UK: IEEE Press, 2009: 565-571.
[7] TSAI L W, JOSHI S A. Kinematics and optimization of a spatial 3-UPU parallel manipulator [J]. Journal of Mechanical Design ASME, 2000, 122: 439-446.
[8] HUANG Tian, LI Meng, LI Zhan-xian, CHETWYND D G, WHITEHOUSE D J. Optimal kinematic design of 2-DOF parallel manipulators with well-shaped workspace bounded by a specified conditioning index [J]. IEEE Transactions on Robotics and Automation, 2004, 20(3): 538-542.
[9] CLAVEL R. Device for the movement and positioning of an element in space: US 4976582 [P]. 1990-12-11.
[10] PIERROT F, DAUCHEZ P, FOURNIER A. HEXA: A fast six-DoF fully-parallel robot [C]// Proceedings of 5th International Conference on Advanced Robotics (ICAR). Pisa, Italy: IEEE Press, 1991: 1158-1163.
[11] MILLER K. Synthesis of a manipulator of the new UWA robot [C]// Proceedings of Australian Conference on Robotics and Automation. Brisbane, Australia: QLD Press, 1999: 228-233.
[12] BEHZADIPOUR S, KHAJEPOUR A, DEKKER R, CHAN E. DeltaBot: A new cable-based Ultra high speed robot [J]. ASME Dynamics Systems and Control Division (Publication) DSC, 2003, 72(1): 533-537.
[13] BEHZADIPOUR S, KHAJEPOUR A. Stiffness of cable-based parallel manipulators with application to stability analysis [J]. ASME Journal of Mechanical Design, 2006, 128(1): 303-310.
[14] HUANG Tian, LI Zhan-xian, LI Meng. 2-DOF translational parallel robot with rotational joints: CHN, CN1355087A [P]. 2002-06-26. (in Chinese)
[15] HUANG Tian, LI Zhan-xian, LI Meng. Conceptual design and dimensional synthesis of a novel 2-DOF translational parallel robot for pick-and-place operations [J]. ASME Journal of Mechanical Design, 2004, 126(3): 449-455.
[16] HUANG Tian, LIU Hai-tao, Zhao Xue-man. Spatial three translational parallel mechanism with parallelogram link: CHN, CN1785607 [P]. 2006-06-14. (in Chinese)
[17] O’BRIEN T W. General soultion of suspended cable problem [J]. ASCE Journal of Structural Division, 1967, 93(1): 1-26.
[18] IRVINE H M. Static of suspended cable [J]. ASCE Journal of Structural Division, 1975, 90(3): 89-123.
[19] RAID K. Some modeling aspects in the nonlinear finite element analysis of cable supported bridges [J]. Computers and Structures, 1999, 71(4): 397-412.
[20] RUSSELL J C, LARDNER T J. Statics experiments on an elastic catenary [J]. ASCE Journal of Structural Division, 1997, 123(12): 1322-1324.
(Edited by YANG Bing)
Foundation item: Projects(50175295, 50675151) supported by the National Natural Science Foundation of China; Project(11JCZDJC22700) supported by Tianjin Science and Technology Program, China; Project(2007AA042001) supported by the National High Technology Research and Development Program of China
Received date: 2009-09-01; Accepted date: 2009-12-23
Corresponding author: SONG Yi-min, Professor, PhD; Tel: +86-22-27403434; E-mail: ymsong@tju.edu.cn