网络首发时间: 2016-07-07 16:26

稀有金属 2018,42(03),285-290 DOI:10.13373/j.cnki.cjrm.xy16040009

<100>P型4英寸无位错锗单晶的研制

高欢欢 黎建明 冯德伸 王霈文 李葳

摘 要：

从4英寸无位错锗单晶的生长温度梯度条件出发, 设计开发了直拉法生长4英寸无位错锗单晶的双加热器热场系统;并对其热场进行了一系列的数值模拟研究, 获得了4英寸无位错锗单晶的温度分布、轴向和径向的温度梯度分布以及热应力的分布结果:双加热器热场系统生长的锗单晶中轴向温度梯度在0.1⁰.6 K·cm-1范围内, 径向温度梯度为0.02⁰.26 K·cm-1;锗单晶中局部区域的热应力值超过了锗单晶的临界切应力1 MPa, 其他区域的热应力小于临界切应力。实验将双加热器热场系统中生长的无位错锗单晶, 按要求切取测试片后进行位错腐蚀测量研究, 获得测试片的位错密度和锗晶体的位错纵向分布。论文研究结果表明, 锗单晶晶体中的应力分布数值模拟预期结果与实验生长的锗单晶位错腐蚀实验研究结果一致:该双加热器热场系统适合拉制4英寸无位错锗单晶;其位错呈离散分布, 位错密度为350⁴80 cm-2。

关键词：

无位错;锗单晶;加热器结构;温度梯度;

中图分类号： TN304.11

作者简介：高欢欢 (1989-) , 女, 河北人, 硕士研究生, 研究方向:晶体生长;E-mail:danyanhuan@163.com;;黎建明, 教授;电话:13370118561;E-mail:jmli66@126.com;

收稿日期：2016-04-13

基金：河北省重大科技成果转化专项项目 (13040603Z) 资助;

Development of 4-Inch P-Type Dislocation-Free Germanium Crystal with < 100 > Crystallographic Orientation

Gao Huanhuan Li Jianming Feng Deshen Wang Peiwen Li Wei

GRINM Electro-Optic Materials Co., Ltd., Beijing General Reserch Institute for Nonferrous Metals

Abstract：

Based on the growth temperature gradient of 4-inch dislocation-free germanium single crystal, a double heaters thermal field system in which 4-inch dislocation-free germanium single crystal could grow was designed and developed. Temperature, temperature gradient and stress distribution in the crystal were obtained by numerical simulation. The outcomes by numerical simulation showed that the axial temperature gradient was in the range of 0. 1 ~ 0. 6 K·cm-1, the radial temperature gradient was kept in the range of0. 02 ~ 0. 26 K·cm-1, and the maximum thermal stress value in some areas of crystal exceeded barely the critical shear stress. In addition, the growth experiment of dislocation-free germanium crystal was carried out in the thermal field, and the dislocation corrosion experiment was studied. Then the radial distribution and longitudinal distribution of dislocations in germanium were obtained. The prospective results of numerical simulation about stress distribution were in agreement with those of the experimental study on the dislocation. The main results were as follows: the double heaters system could be used for growing 4-inch dislocation-free germanium, the density of dislocation was in the range of 350 ~ 480 cm-2 and etched pits of dislocation were scattered.

Keyword：

dislocation-free; germanium crystal; structure of heaters; temperature gradient;

Received： 2016-04-13

砷化镓太阳电池转换效率高、可靠性高, 已成为主流高效空间电源^[1,2]。锗因机械强度高, 易制备大尺寸单晶, 且与砷化镓的晶格常数相近等优点, 使得其单晶片可用作砷化镓空间太阳电池的衬底片^[3,4]。而P型锗单晶衬底片上制作的砷化镓空间太阳电池的效率更高、综合性能更好, P型锗单晶成为砷化镓空间太阳电池的主要衬底材料^[5,6,7]。

锗单晶中的位错缺陷影响外延层质量, 降低太阳电池的转换效率^[8]。降低位错密度一直是低位错大直径锗单晶研究的难点和热点^[9]。关于无位错大直径锗单晶, 国外研究较早, 2006年, Umicore公司报道实验研制出Φ=300 mm的无位错 (EPD<500 cm^-2) 锗单晶^[10];2008年, 北京有色金属研究总院生长出位错密度为3000 cm^-2的4英寸锗单晶^[11], 其技术水平与国外差距较大, 已不能满足我国空间太阳电池发展需求。目前我国外延所需4英寸P型无位错锗衬底片主要依赖进口, 成为空间电源发展的瓶颈, 因此开展4英寸P型无位错锗单晶研究具有重大实际应用价值和战略意义。

1 无位错锗单晶的热场设计

1.1 无位错锗单晶的生长条件

晶体生长驱动力来源于温度梯度。晶体中只要存在温度梯度, 就产生热应力, 当晶体中的热应力超过产生位错的临界应力时, 晶体中就产生位错^[12], 晶体中的位错密度 (N_d) 与温度梯度的关系式为^[13]:

式中β为热膨胀系数 (℃^-1) , b为Burgs矢量值 (mm) , G为切变模量 (Pa) , τ为临界应力 (Pa) , R为单晶半径 (mm) , L为单晶长度 (mm) , 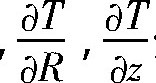分别为固液界面处的径向和轴向温度梯度 (K·cm^-1) 。假设生长无位错锗单晶, 即N_d=0, 由上述两公式可得晶体生长无位错单晶的必要条件即生长无位错单晶的临界值分别为:

由 (3) , (4) 可知, 生长无位错单晶的临界径向温度梯度与晶体长度成反比, 临界轴向温度梯度与生长晶体的半径成反比。对于锗, β=6.1×10^-6℃^-1, b=5.6575×10^-7mm, G=41 GPa, τ_c=1 MPa^[14]。生长直径为4英寸、长度为100 mm的无位错锗单晶时, 计算可得:临界径向温度梯度为0.40 K·cm^-1, 临界轴向温度梯度为0.80 K·cm^-1。

1.2 无位错锗单晶生长热场的加热器设计

加热器是晶体生长热场的关键部件, 其结构和形状设计决定晶体生长的静态热场。单加热器结构条件下的热场温度梯度较大且低温度梯度区域较小, 难以满足无位错锗单晶的生长条件, 通过反复模拟优化及实验, 最终设计了如图1所示的双加热器结构及保温系统。该加热器为石墨电阻加热, 分为主加热器和底加热器, 其功率均可单独调节。主加热器分为渐变和直筒两部分, 石墨电阻片的顶端最薄, 逐渐变厚, 降低了热场上部的温度梯度;底加热器呈圆环形, 提高了热场底部的温度并加长下部分的低温度梯度区域。该热场保温系统采用石墨碳毡复合结构, 增强了保温, 降低了热场的温度梯度, 扩大了低温度梯度的有效区间。

2 实验

2.1 数值模拟实验

本文以TDR-Z80单晶炉为原型, 采用渐变双加热器结构模型, 使用有限元方法对直拉法锗单晶的生长过程进行模拟。在柱坐标中, 锗单晶的生长具有圆柱对称性, 籽晶轴为对称轴, 则在二维模拟中只需要得出右半部分的结果即可。模拟过程中晶体生长炉采用冷却水冷却, 设定边界条件为300 K, 其他参数设置如表1^[15]所示。

2.2 锗单晶生长实验

锗单晶生长设备为国产TDR-Z80单晶炉。实验采用<100>晶向籽晶, 掺杂剂为镓, 原料为7 N以上的高纯区熔锗, 装料量为30 kg。单晶生长过程中, 将高纯锗原料和掺杂剂装入石墨坩埚中, 并将坩埚置于热场合适位置, 抽真空后, 充入氩气, 加热升温原料熔化后, 调节主加热器与底加热器功率稳定一段时间, 获得稳定的低温度梯度热场;进行引晶、放肩, 晶体尺寸达到要求后进行等径控制, 转入程序自动控制, 其具体工艺参数如表2, 待晶体长度达到100 mm后收尾;最后晶体进行原位退火, 降温至室温。

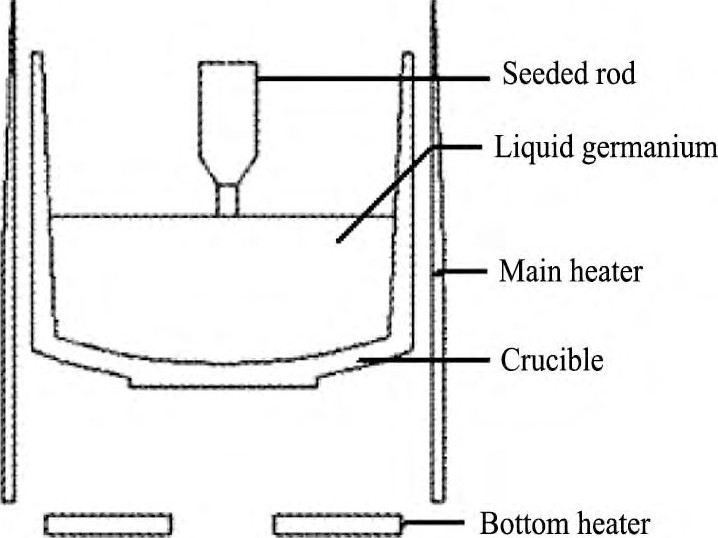
图1 双加热器结构示意图Fig.1 Schematic diagram of double heaters structure

表1 数值模拟中的参数设置Table 1 Parameter settings in numerical simulation  下载原图

表1 数值模拟中的参数设置Table 1 Parameter settings in numerical simulation

2.3 位错腐蚀研究

2.3.1 位错腐蚀测量

将生长的<100>锗单晶在测试要求位置处切取厚度为2~3 mm测试样片, 依据GB/T5252-2006位错腐蚀测量标准要求, 用金刚砂将样片表面进行研磨, 消除切割引入的痕迹及损伤;然后在温度为45~60℃的抛光液 (HF∶HNO₃=1∶1~3 (体积比) ) 中抛光30 s, 温度为13~18℃的腐蚀液 (HF∶HNO₃∶Cu (NO₃) ₂ (10%水溶液) =2∶1∶1 (体积比) ) 中浸泡5 min, 显示出位错坑;最后用去离子水冲洗并吹干后在型号为GX51的显微镜下采用九点法 (如图2所示) 观察位错 (图3所示) 并记录位错密度。

2.3.2 锗单晶位错的纵向分布研究

实验将双加热器热场系统中生长的5根典型无位错锗晶体, 沿晶体生长方向按间隔10或20 mm不等从头部向尾部分别切取测试片后进行位错腐蚀测量, 获得每个测试片的位错密度和每根锗晶体的位错纵向分布。

表2 晶体生长实验中的工艺参数Table 2 Parameters in crystal growth experiment  下载原图

表2 晶体生长实验中的工艺参数Table 2 Parameters in crystal growth experiment

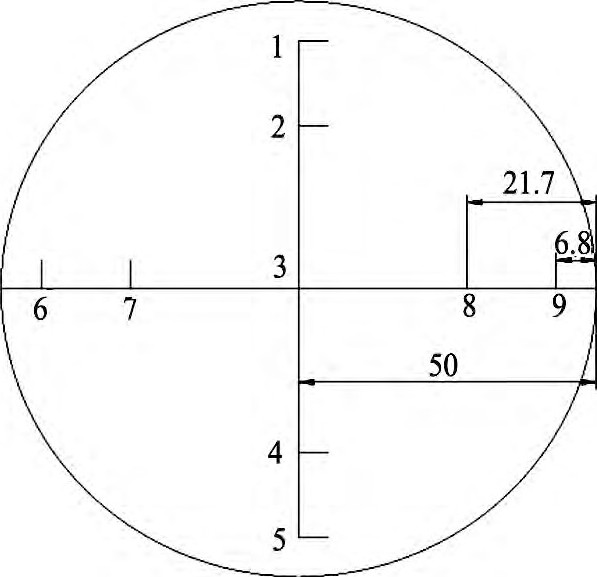
图2 九点法测位错示意图Fig.2Schematic view of measuring dislocation density with nine law (mm)

图3<100>晶向锗单晶的位错图像Fig.3Dislocation image of<100>germanium crystal with<100>

3 结果与讨论

3.1 数值模拟

图4~6分别为双加热器热场系统中生长无位错锗单晶的温度分布、温度梯度分布和应力分布数值模拟图。图4中相邻等温线间的温度差为1K, 可看出:晶体内的等温线分布稀疏即晶体内的轴向温度梯度较小;等温线趋于水平, 晶体中的径向温度变化较小, 即径向温度梯度小。图5证实了轴向和径向温度梯度均较小。轴向温度梯度从固液界面向晶体头部方向逐步增大, 其数值在0.1~0.6 K·cm^-1范围内 (如图5 (a) 所示) ;径向温度梯度从籽晶轴往晶体外沿方向基本稳定, 变化较小, 其数值在0.02~0.26 K·cm^-1左右 (如图5 (b) 所示) 。因此从图5可知无位错锗单晶中轴向和径向温度梯度均小于产生位错所需的临界温度梯度值。图6晶体中的应力分布结果可看出, 晶体中有某些局部区域的应力大于锗单晶的临界切应力1 MPa;其他大部分区域的应力小于临界切应力。

图4 晶体中温度分布的模拟结果Fig.4 Simulation results of temperature distribution in crystal

图5 晶体中温度梯度分布的模拟结果Fig.5 Simulation results of temperature gradient distribution in crystal

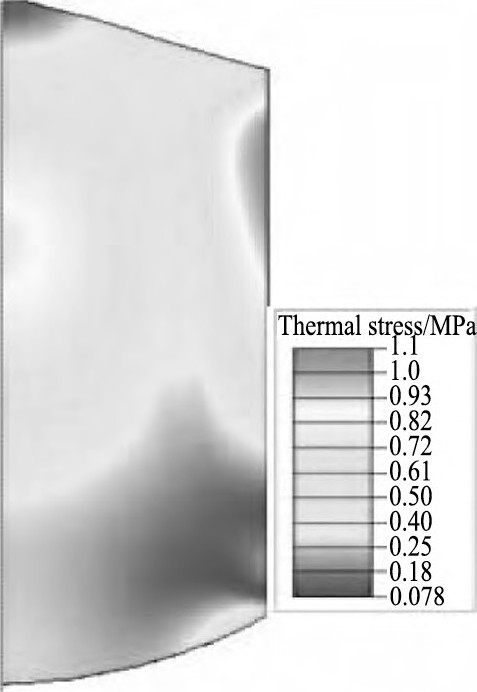
图6 晶体中应力的模拟结果Fig.6 Simulation results of thermal stress in crystal

3.2 实验研究

图7中为实验拉制的直径为4英寸长度为100mm的无位错锗单晶。从图7中可知双加热器晶体生长系统能够拉制出直径为4英寸无位错锗单晶, 且晶体外形较好, 表明该热场系统温度梯度虽小, 但拉制4英寸无位错锗单晶过程可控。表3列出了5根无位错锗晶体的各个测试片的位错密度。由表3可看出, 同一根锗晶体中头部与尾部位错密度相差不大, 较为均匀, 均在350~480 cm^-2范围内, 但从头部到尾部仍可观察到位错密度有稍许增加的趋势;从表3中还可看出, 不同锗晶体中相同位置的位错密度变化小, 结合位错腐蚀图像研究 (如图3所示) 可知, <100>晶向锗单晶的位错分布离散, 没有位错堆出现, 数值也在350~480 cm^-2范围内, 锗晶体一致性、重复性好。

3.3 数值模拟与实验对比研究

图6晶体中某些局部区域的热应力大于锗单晶的临界切应力1 MPa, 基于“完全弛豫弹性应力”的近似理论^[16], 这些区域产生引起弹性应力场, 而引入位错使之变成不均匀范性变形, 以消驰弹性应力场。由于这些热应力大区域是随机且离散, 因此位错产生应该也是随机且离散的。这些预期结果在位错腐蚀研究的实验中得到证实, 结果一致:晶体中的位错分布离散, 纵向和径向位错密度分布较为均匀, 晶体位错密度一致性、重复性好。

图7 直径为4英寸长度为100 mm的无位错锗单晶Fig.74-inch dislocation-free germanium crystal with a length of 100 mm

表3 锗晶体的位错密度Table 3Etch pit density of germanium crystals (cm^-2)   下载原图

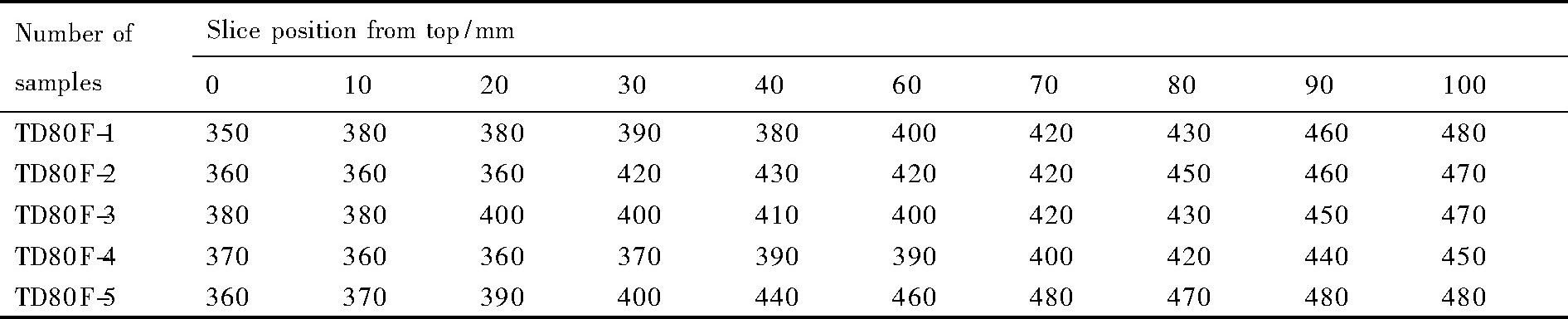
表3 锗晶体的位错密度Table 3Etch pit density of germanium crystals (cm^-2)

4 结论

通过对双加热器结构系统进行的数值模拟研究及其中生长的无位错锗单晶的位错密度实验结果对比分析、研究, 得出如下结论:

1.双加热器热场系统能拉制出直径为4英寸长度为100 mm的无位错锗单晶, 且锗晶体位错密度重复性好。

2.数值模拟结果表明该热场系统中温度梯度小于4英寸无位错锗单晶生长条件的理论值, 锗单晶中某些局部区域最大热应力值与锗单晶的临界切应力相近。

3.应力分布数值模拟预期结果与锗单晶位错腐蚀实验研究结果一致:晶体中的位错分布均匀、离散, 位错密度为350~480 cm^-2。

参考文献

[1] Lin G J.Research progress and market situation of high efficiency solar cells in the spotlight[A].China Chemical and Physical Power Industry Association Solar Photovoltaic Branch Third Academic Symposium[C].Shanghai, 2014.43. (林桂江.聚光高效多节太阳电池的研究进展和市场化情况[A].中国化学与物理电源行业协会太阳能光伏分会第三届学术研讨会[C].上海, 2014.43.)

[2] Qiu D D, Yang Y F, Jin H S.Classifications and development of space solar cells[J].Power Technology, 2013, 137 (11) :2070. (邱东东, 杨永枫, 金华松.空间用太阳电池的种类和发展[J].电源技术, 2013, 137 (11) :2070.)

[3] Tu H L Translated.Germanium Semiconductor Materials and Devices[M].Beijing:Metallurgical Industry Press, 2010.43. (屠海令译.半导体锗材料与器件[M].北京:冶金工业出版社, 2010.43.)

[4] Fu R, Chen N F.Latest technological development of highly efficientⅢ-V mult-junction solar cells[J].Materials Review A, 2015, 29 (4) :124. (付蕊, 陈诺夫.基于Ⅲ-V族材料制备的高效多结太阳电池最新技术进展[J].材料导报A, 2015, 29 (4) :124.)

[5] Martin A Green, Keith Emery, Yoshihiro Hishikawa, Wilhelm Warta, Ewan D Dunlop.Solar cell efficiency tables (version 41) [J].Progress in Photovoltaics:Research and Applications, 2013, 21 (1) :1.

[6] Vanhellemont J, Simoen E.Brother silicon, sister germanium[J].Journal of the Electrochemical Society, 2007, 157 (7) :572.

[7] Li M M, Su X P, Feng D S, Wang X W, Zuo J.New development of germanium single crystal applied in Ga As/Ge solar cells[J].Metallic Functional Materials, 2010, 17 (6) :78. (李苗苗, 苏小平, 冯德伸, 王学武, 左建.Ga As/Ge太阳能电池用锗单晶的研究新进展[J].金属功能材料, 2010, 17 (6) :78.)

[8] Dinesh Rakwal, Eberhard Bamberg.Slicing, cleaning and kerfnalysis of germanium wafers machined by wire electrical dicharge machining[J].Journal of Materials Processing Technolgy, 2008, 209 (8) :3740.

[9] Toshinori Taishi, Yutaka Ohno, Ichiro Yonenaga.Reduction of grown-in dislocation density in Ge Czochralski-grown from the B2O3-partially-covered melt[J].Journal of Crystal Growth, 2009, 311 (22) :4615.

[10] Ben Depuydt, Antoon Theuwis, Igor Romandic.Ger-manium:From the first application of Czochralski crystal growth to large diameter dislocation free wafers[J].Materials Science in Semiconductor Processing, 2006, 9 (4-5) :437.

[11] Feng D S, Li N, Su X P, Yang H, Min Z D.Growth of 4 inch low dislocation germanium monocrystal[J].Chinese Journal of Rare Metals, 2008, 32 (1) :34. (冯德伸, 李楠, 苏小平, 杨海, 闵振东.4英寸低位错锗单晶生长[J].稀有金属, 2008, 32 (1) :34.)

[12] Zuo J L, Feng D S, Li N.Influence factors of germanium monocrystal dislocation density[J].Chinese Journal of Rare Metals, 2010, 34 (5) :726. (左建龙, 冯德伸, 李楠.锗单晶中位错密度的影响因素[J].稀有金属, 2010, 34 (5) :726.)

[13] She S M.Semiconductor Silicon Material Science[M].Changsha:Central South University Press, 1992.194. (佘思明.半导体硅材料学[M].长沙:中南工业大学出版社, 1992.194.)

[14] Chernov A A.Modern Crystallography III:Crystal Growth (Springer Series in Solid-Stste Science) [M].Berlin:Springer-Verlag, 1984.36.

[15] Bogaert N, Van den, Dupret F.Dynamic global simulation of the Czochralski process I.Principle of the method[J].Journal of Crystal Growth, 1997, 171:65.

[16] Min N B.Physical Basis of Crystal Growth[M].Shanghai:Shanghai Science and Technology Press, 1982.473. (闵乃本.晶体生长的物理基础[M].上海:上海科学技术出版社, 1982.473.)