J. Cent. South Univ. Technol. (2007)06-0842-06
DOI: 10.1007/s11771-007-0160-7

Influences of nonassociated flow rules on seismic bearing capacity factors of strip footing on soil slope by energy dissipation method
YANG Xiao-li(杨小礼), GUO Nai-zheng(郭乃正), ZHAO Lian-heng(赵炼恒), ZOU Jin-feng(邹金锋)
(School of Civil and Architectural Engineering, Central South University, Changsha 410075, China)
Abstract:Seismic bearing capacity factors of a strip footing placed on soil slope were determined with both associated and nonassociated flow rules. Quasi-static representation of earthquake effects using a seismic coefficient concept was adopted for seismic bearing capacity calculations. A multi-wedge translational failure mechanism was used to obtain the seismic bearing capacity factors for different seismic coefficients and various inclined angles. Employing the associated flow rule, numerical results were compared with the published solutions. For bearing capacity factors related to cohesion and equivalent surcharge load, the maximum difference approximates 0.1%. However, the difference of bearing capacity factor related to unit weight is larger. With the two flow rules, the seismic bearing capacity factors were presented in the form of design charts for practical use. The results show that seismic bearing capacity factors related to the cohesion, the equivalent surcharge load and the unit weight increase greatly as the dilatancy angle increases, and that the nonassociated flow rule has important influences on the seismic bearing capacity.
Key words: nonassociated flow rule; seismic bearing capacity factor; earthquake
1 Introduction
The estimation of seismic bearing capacity is requirement in the foundation design subjected to earthquake loads. The seismic bearing capacity of a shallow footing is commonly expressed by Terzaghi’s equation. Using Terzaghi’s equation, the bearing capacity is underestimated. Many investigations have been attempted to modify the Terzaghi’s solution using limit equilibrium method, characteristic method, limit analysis method and numerical methods based on either the finite element or finite difference. These seismic calculations are only valid for a situation where the foundations are placed on horizontal ground surfaces with associated flow rule.
In practice, the determination of the seismic bearing capacity factors for foundations on soil slope is a very important issue for most engineers. For example, many bridge abutments and retaining walls involve the construction of strip footing on soil slopes in earthquake zones. However, the published literature is very limited in this area. KUMAR and MOHAN-RAO[1] used a method of stress characteristics to estimate the seismic bearing capacity factors of a foundation on sloping ground surface. Limit equilibrium solutions to the same problem are presented in Refs.[2-3]. However, those literatures focus on bearing capacity calculation with an associated flow rule and limit equilibrium method.
In the case of dense granular materials, a key factor in constitutive behavior is described as the characteristic of dilatancy angle, which is different from friction angle. According to plasticity theory of geomaterials, dilatancy presence means the geomaterials follow the nonassociated flow rule, which influences the seismic bearing capacity. A number of researchers have employed nonassociated flow rule to calculate static bearing capacity of a strip footing on horizontal ground surface[3-4]. In this paper, the seismic bearing capacity of a strip footing on soil slope was investigated in the framework of limit analysis theory with associated and nonassociated flow rules. The strip shallow footing was placed on homogenous and isotropic soil slope where the effects of earthquake forces were considered. The earthquake forces can be replaced with different inertia forces. These inertia forces concern the soil mass weight, the surcharge, and the base shear load. The effects of associated and nonassociated flow rules on seismic bearing capacity were examined, and some charts of seismic bearing capacity factors with different slope inclination angles were presented for practical use in engineering.
2 Upper bound analysis with earthquake
The seismic bearing capacity qu of the strip footing on soil slope is equal to the vertical ultimate load that the foundation can withstand at the state of incipient failure divided by the base area of the strip footing, which is often expressed as
qu=cNc+q0Nq+0.5γB0Nγ (1)
where B0 is the footing width, Nc, Nq and Nγ are the bearing capacity factors related to the cohesion c, the equivalent surcharge load q0 and the unit weight γ, respectively. An earthquake has two possible effects on the seismic bearing capacity of foundations on soil slope. One is to increase the driving forces, and the other is to decrease the shearing resistance of the soil masses. The reduction in the shearing resistance of the soil masses during an earthquake is in effect only when the magnitude of the earthquake exceeds a certain limit and the ground conditions are favorable for such a reduction. In the present analysis, only the increase of the driving forces was investigated under an earthquake, and the shearing strength was assumed unaffected. A constant horizontal seismic coefficient kh was assumed for the entire soil masses involved, which was the same as the hypothesis in seismic bearing capacity calculations by some researchers[5-11].
2.1 Nonassociated flow rule
The plasticity theory indicates that, if the dilatancy angle is not identical to the friction angle, the material follows a nonassociated flow rule. According to the nonassociated flow rule, the velocity at velocity discontinuities inclines a dilatancy angle with respect to velocity discontinuity line. The dilatancy angle varies from zero to the soil friction angle. Correspondingly, dilative coefficient, η, which relates the dilatancy angle to the soil friction angle, is defined as
η=ψ/φ (2)
where φ is the friction angle and ψ is a dilatancy angle. Theoretically, the magnitude of dilative coefficient is 0≤η≤1. The case η=1 indicates that the material follows an associated flow rule. For a coaxial nonassociated flow rule, if the soil mass is assumed to follow Mohr-Coulomb failure criterion, the following relationships can consider the dilatacy of the material, as shown in Refs.[3, 12-13].
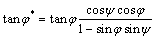 (3)
(3)
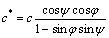 (4)
(4)
where c is cohesion in the linear Mohr-Coulomb failure, c* and φ* are the modified cohesion and friction angle for the upper bound analysis when the material follows a coaxial nonassociated flow rule. Eqns. (3) and (4) was used to calculate static bearing capacity of a strip footing on horizontal ground surface with limit analysis method[3, 14-15].
2.2 Multi-wedges translation mechanism
In the modeling study, a multi-wedge translation failure mechanism was used to calculate seismic bearing capacity of a strip footing on soil slope, as shown in Fig.1. The potential sliding soil is divided into a number of triangular wedges by a series of inclined straight lines. Each of triangular wedges moves as a rigid wedge. The geometry of ith wedge is characterized by the length of the base di, the angles αi and βi, and the length of interface Li (i=1,…, n). The angles αi and βi (i=1,…, n) are unspecified. The wedge velocity and relative velocity of the ith wedge with respect to the (i+1)th wedge along the interface are determined by the velocity hodograph. Such, if the velocity of the first wedge is given, the velocities and relative velocities of all wedges can be found. The velocity of the first wedge is often assumed to be unit.
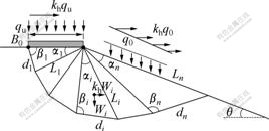
Fig.1 External forces for failure mechanism of footing on soil slope
2.3 Calculations of work rate and energy
The work rate done by the external load and internal energy dissipation rates can be calculated by superposition. The external rate of work is done by the surcharge q0 on the inclined surface, the soil mass weight Wi (i=1,…, n), the ultimate bearing capacity qu, and earthquake forces replaced with the inertia forces. These inertia forces concern the base shear load khqu, the surcharge khq0, and the soil mass weight khWi (i=1,…, n). Since the soil mass is regarded as perfectly rigid and no general plastic deformation is permitted to occur, the internal energy is dissipated only along velocity discontinuity di (i=1, …, n) between the soil at rest and the soil in motion, and along the relative velocity discontinuity interface Li (i=1,…, n-1) between adjoining two wedges. Equating the work rate of external loads to the total internal energy dissipation rates, an objective function can be obtained. The lowest upper bound solution is minimizing the objective function[16-21]. In generally, upper bound solution can be improved by increasing the number of triangular wedges. In the present analysis, the triangular wedge number n is equal to 15, which means that the minimization procedure is made with regard to 30 variables.
3 Numerical results
Examples selected include: 1) for the strip footing on horizontal ground surface, comparisons are made between the present seismic bearing capacity using energy dissipation method and the published solution using stress characteristics method with associated flow rule, and 2) seismic bearing capacity factors with nonassociated flow rules for different inclined angles are presented for practical use.
3.1 Comparisons
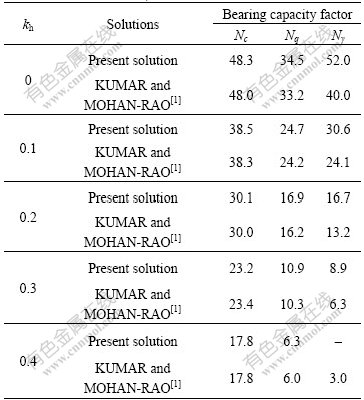
For foundation on soil slope, the present solutions using the energy dissipation method are presented and compared with the published solutions of KUMAR and MOHAN-RAO[1] using stress characteristics method. Table 1 presents the values of bearing capacity factors corresponding to φ=40? and θ=15? when the effects of horizontal earthquake forces are considered. It is found from Table 1 that the present bearing capacity factors Nc and Nq are almost equal to those of KUMAR and MOHAN-RAO[1]. However, the factor Nr is larger thanthat of KUMAR and MOHAN-RAO[1]. It is noted that the numerical results of KUMAR and MOHAN-RAO[1]
in Table 1 are obtained from charts, and that the bearing capacity factor Nγ corresponds to one side failure mechanism.
Table 1 Comparisons of bearing capacity factors for φ=40? and θ=15?
3.2 Effects of seismic coefficient
To investigate how the seismic bearing capacity is influenced by earthquake forces when the foundation rests on a soil slope with associated flow rule, Fig.2 shows a strip footing on a soil slope with the slope angle θ varying from 5? to 25? while horizontal seismic coefficient kh is equal to 0.1 and 0.2. From Fig.2, it is found that the seismic bearing capacity factors become small as the seismic coefficient kh increases. For example, for the case of θ=10? and φ=30?, the value of the seismic bearing capacity factor Nc is 20.23 at kh=0.1, while the value is 16.41 at kh=0.2. The absolute difference is 3.82. Design charts for seismic bearing capacity factors Nc, Nq and Nγ are presented for practical use.
3.3 Effects of dilative coefficient
As seen from Fig.3, with the coaxial nonassociated flow rule, it is found that the dilatancy angle has a significant influence on the seismic bearing capacity. The larger the dilatancy angles, the lager the values of the seismic bearing capacity factors are. For example, for the case of θ=10?, kh=0.1 and φ=30?, the value of the seismic bearing capacity factor Nc is 19.66 at η=0.75, while the value of the seismic bearing capacity factor Nc is 16.37 at η=0.25. The absolute difference is 3.27.
The designed figures for seismic bearing capacity factors are presented for practical use in geotechnical engineering when the dilative coefficients are equal to 0.25, 0.50 and 0.75. With the energy dissipation method of plastic mechanics in limit analysis, numerical results show that the soil dilation angle has an important effect on the seismic bearing capacity for the strip footing on soil slope. When the soil dilation angle keeps constant, the seismic bearing capacity becomes small as the slope angle θ increases.
According to the comparisons between Fig.2 and Fig.3 with the same seismic coefficient and the same slope angle, the seismic bearing capacity factor Nc with associated flow rule is greater than that with nonassociated flow rule. For example, for the case of θ=10?, kh=0.1 and φ=30?, the value of the seismic bearing capacity factor Nc is 20.23 at η=1.0 with associated flow rule, while the that of the seismic bearing capacity factor Nc is 16.37 at η=0.25 with nonassociated flow rule. The absolute difference is 3.86.
4 Conclusions
1) Incorporating the effects of horizontal earthquake forces, the seismic bearing capacity factors of a strip footing on soil slope are investigated by using energy dissipation method with both associated and nonassociated flow rules.
2) For the strip footing on soil slope, effects of the seismic coefficient on seismic bearing capacity factors are discussed with associated flow rule. With the increase of seismic coefficient, seismic bearing capacity factors decrease. Design charts for the seismic bearing capacity factors are presented for practical use with the associated flow rule.
3) For the strip footing on soil slope, effects of the nonassociated flow rule on seismic bearing capacity factors are discussed. With the constant seismic coefficient and slope angle, the seismic bearing capacity factors increase as dilative coefficient increases. The design charts for the seismic bearing capacity factors for practical use are presented with the nonassociated flow rule.
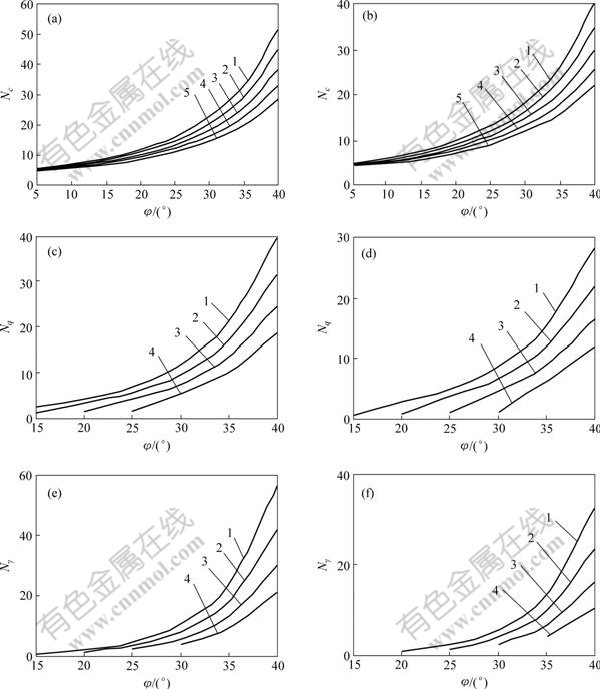
Fig.2 Seismic bearing capacity factors of foundations on soil slopes with associated flow rule
(a), (c), (e) kh=0.1; (b), (d), (f) kh=0.2
θ/(?): 1—5; 2—10; 3—15; 4—20; 5—25
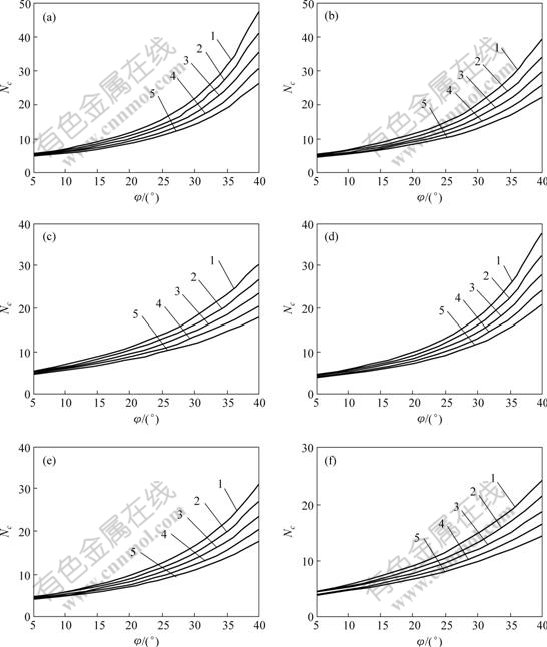
Fig.3 Seismic bearing capacity factor of foundations on soil slopes with nonassociated flow rule
(a) kh=0.10, η=0.75; (b) kh=0.10, η=0.50; (c) kh=0.10, η=0.25; (d) kh=0.20, η=0.75; (e) kh=0.20, η=0.50; (b) kh=0.20, η=0.25
θ/(?): 1—5; 2—10; 3—15; 4—20; 5—25
References
[1] KUMAR J, MOHAN-RAO V B K. Seismic bearing capacity of foundations on slopes[J]. Geotechnique, 2003, 53(3): 347-361.
[2] KUMAR J, KUMAR N. Seismic bearing capacity of rough footings on slopes using limit equilibrium[J]. Geotechnique, 2003, 53(3): 363-369.
[3] MICHALOWSKI R L. An estimate of the influence of soil weight on bearing capacity using limit analysis[J]. Soils and Foundations, 1997, 37(4): 57-64.
[4] FRYDMAN S, BURD H J. Numerical study of bearing capacity factor Nγ[J]. ASCE Journal of Geotechnical and Geoenvironmental Engineering, 1997, 123(1): 20-29.
[5] BOLTON M D, LAU C K. Vertical bearing capacity factors for circular and strip footings on Mohr-Coulomb soil[J]. Canadian Geotechnical Journal, 1993, 38(5): 1090-1096.
[6] BUDHU M, AL-KARNI A. Seismic bearing capacity of soils[J]. Geotechnique, 1993, 43(1): 181-187.
[7] CHEN W F. Limit Analysis and Soil Plasticity[M]. Amsterdam: Elsevier Scientific Publishing Company, 1975.
[8] RICHARDS R, ELMS D, BUDHU M. Seismic bearing capacity and settlement of foundations[J]. ASCE Journal of Geotechnical and Geoenvironmental Engineering, 1993, 119(4): 662-674.
[9] YANG Xiao-li, LI Liang, YIN Jian-hua. Seismic and static stability analysis of rock slopes by a kinematical approach[J]. Geotechnique, 2004, 54(8): 543-549.
[10] YANG Xiao-li, YIN Jian-hua. Estimation of seismic passive earth pressure with non-linear failure criterion[J]. Engineering Structures, 2006, 28(3): 342-348.
[11] YANG Xiao-li. Upper bound analysis of active earth pressure with different fracture surface and nonlinear yield criterion[J]. Theoretical and Applied Fracture Mechanics, 2007, 47(1): 46-56.
[12] DAVIS E H. Theories of Plasticity and the Failure of Soil Masses[M]. London: Butterworths, 1968: 341-380.
[13] DRESCHER A, DETOURNAY C. Limit load in translational failure mechanisms for associative and non-associative materials[J]. Geotechnique, 1993, 43(3): 443-456.
[14] MICHALOWSKI R L, SHI L. Bearing capacity of footings over two-layer foundation soils[J]. ASCE Journal of Geotechnical Engineering, 1995, 121(5): 421-427.
[15] SOUBRA A H. Upper-bound solution for bearing capacity of foundations[J]. ASCE Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(1): 59-68.
[16] YANG Xiao-li, YIN Jian-hua. Upper bound solution for ultimate bearing capacity with a modified Hoek-Brown failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(4): 550-560.
[17] YANG Xiao-li, ZOU Jin-feng. Stability factors for rock slopes subjected to pore water pressure based on the Hoek-Brown failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(7): 1146-1152.
[18] YANG Xiao-li. Seismic displacement of rock slopes with nonlinear Hoek-Brown failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 948-953.
[19] YANG Xiao-li, YIN Jian-hua. Slope stability analysis with nonlinear failure criterion[J]. Journal of Engineering Mechanics, 2004, 130(3): 267-273.
[20] UKRITCHON B, WHITTLE A J, KLANGVIJIT C. Calculations of bearing capacity factor using numerical limit analysis[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(5): 468-474.
[21] YANG Xiao-li, WANG Zhi-bin, ZOU Jin-feng, et al. Bearing capacity of foundation on slope determined by energy dissipation method and model experiments[J]. Journal of Central South University of Technology, 2007, 14(1): 125-128.
(Edited by CHEN Wei-ping)
Foundation item: Project(200550) supported by the Foundation for the Author of National Excellent Doctoral Dissertation of China; Project(05-0686) supported by the Program for New Century Excellent Talents in University
Received date: 2007-05-12; Accepted date: 2007-07-18
Corresponding author: YANG Xiao-li, Professor; Tel: +86-731-2656248; E-mail: yxnc@yahoo.com.cn