Numerical simulation of influence of material parameters on splitting spinning of aluminum alloy

Huang Liang(黄 亮), Yang He(杨 合), Zhan Mei(詹 梅), HU Li-jin(胡莉巾)

School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China

Received 13 July 2007; accepted 30 September 2007

Abstract: During the splitting spinning process, the material parameters of disk blank have a significant effect on the determination of forming parameters and the quality of deformed blank. The influence laws of material parameters, including yield stress, hardening exponent and elastic modulus, on splitting spinning force, splitting spinning moment, degree of inhomogeneous deformation and quality of flange (average thickness and average deviation angle) were investigated by 3D-FE numerical simulation based on elasto-plastic dynamic explicit FEM under ABAQUS/Explicit environment. The results show that, the splitting spinning force and the splitting spinning moment increase with the increase of yield stress, hardening exponent and elastic modulus. The degree of inhomogeneous deformation increases with the decrease of yield stress and hardening exponent and the increase of elastic modulus. The average thickness of flange increases with the decrease of yield stress and the increase of hardening exponent and elastic modulus. The average deviation angle of upper surface increases with the increase of yield stress and the decrease of hardening exponent and elastic modulus. The average deviation angle of lower surface increases with the decrease of yield stress, hardening exponent and elastic modulus. Meanwhile, the corresponding variation ranges are given. The achievements may serve as an important guide for selecting the reasonable processing parameters of splitting spinning based on different aluminum alloys, and are very significant for optimum design and precision control of the splitting spinning process.

Key words: splitting spinning; material parameters; elasto-plastic dynamic explicit FEM; ABAQUS/Explicit

1 Introduction

The splitting spinning is designed to split a rotational disk blank from the outer rectangular edge into two flanges using a roller called splitting roller with a sharp corner, and then shaping spinning is done by other two or three forming rollers[1], as shown in Fig.1. As a newly special spinning technology, the splitting spinning process is a continuous and local plastic forming process with the characteristics of asymmetry, non-steady state and 3D inhomogeneous deformation followed with the feeds of rollers[2], companied with many advantages, such as high quality, high precision, high efficiency and low cost. Therefore, it can be applied to manufacture a whole wheel or pulley[3] with aluminum alloy or soft steel (in heating condition) in fields of aerospace, automobile, train and ship, as shown in Fig.2.

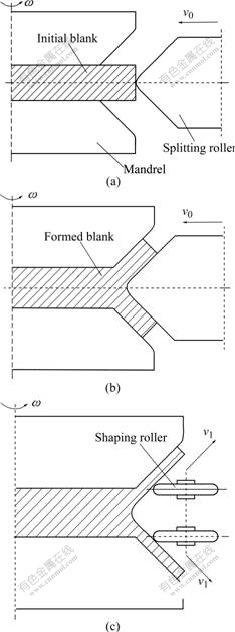
Fig.1 Schematic illustration of splitting spinning process: (a) Before forming; (b) During forming process; (c) Shaping spinning

Fig.2 Production of splitting spinning (whole automobile wheel or pulley)

It must be pointed out that, the materials of disk blank must match the formability during the splitting spinning, and the material parameters of disk blank have a significant effect not only on the determination of forming parameters but also on the quality of deformed blank[4-7]. So far, some researches on splitting spinning have been carried out by experiments and FE numerical simulations[8-9], and very few have focused on the influence of material parameters on the process. Due to the complexity of the splitting spinning process, it is obviously difficult to understand the process purely by analytical or experimental methods. Therefore, it is essential to study the splitting spinning systemically by the FE numerical simulation method. In this work, the influence laws of material parameters, including yield stress σ_s, hardening exponent n and elastic modulus E, on splitting spinning force, splitting spinning moment, degree of inhomogeneous deformation and quality of flange (average thickness and average deviation angle) have been investigated by 3D-FE numerical simulation based on elasto-plastic dynamic explicit FEM under ABAQUS/Explicit environment.

2 3D-FE model of splitting spinning and determination of calculation conditions

2.1 3D-FE model of splitting spinning

During the splitting spinning process, two mandrels rotate at a rotational speed of ω, and splitting roller feeds at a linear speed of ν in the radial direction of disk blank, as shown in Fig.1. Meanwhile, under the effects of the friction between disk blank and splitting roller and the extrusions of two mandrels, disk blank driven by the two mandrels of a rotational speed of ω is split into two flanges from the outer rectangular edge using splitting roller with a sharp corner, which comes into the gaps at the joints between splitting roller and two mandrels. After the forming ends, the radius of disk blank reduces, and two flanges are produced. The simulation result of disk blank is shown in Fig.3. Through the analysis of the flow of material and the figure change of the workpiece in the splitting spinning process[10], a reasonable 3D-FE model has been developed to simulate the splitting spinning process under the ABAQUS/Explicit environment, as shown in Fig.4.

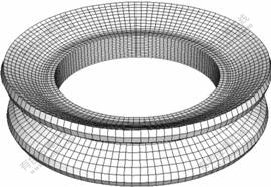
Fig.3 Schematic view of disk blank with two flanges

Fig.4 3D-FE model of splitting spinning under FE software environment of ABAQUS/Explicit

In general, the main characteristics of the proposed model of splitting spinning are as follows:

1) As disk blank is extruded into the deformation zone step by step and then is off the deformation zone after the flanges are generated, an elasto-plastic FE method is used to control the elastic recovery of disk blank with the aims of high computational precision during the splitting spinning process.

2) Based on the quasistatic procedure of splitting spinning and the neglect of inertia effect, the dynamic explicit algorithm is used to avoid the huge computation time and convergence problem of the implicit algorithm for improvement of computation efficiency.

3) Based on the characteristic of the angle between splitting roller and disk blank being 0^o during the splitting spinning process, the velocity boundary conditions are used to definite the mechanics boundary conditions.

4) It’s assumed that the friction on the contact surfaces meets the law of Coulomb friction and remains unchanged during the splitting spinning process.

5) The 8-noded hexahedral continuum elements with quadratic reduced-integration are adopted to mesh homogeneously, which are not susceptible to locking even when being subjected to complicated states of stress. Therefore, the elements are also generally the best choice for the most general stress/displacement simulations. Meanwhile, the concentric circle meshing mode and the adaptive meshing technology are employed to avoid hourglass modes and reduce the distortion of elements [11-12]. Furthermore, meshing is symmetrical to control the mode of zero energy in the axial direction.

2.2 Verification of 3D-FE model of splitting spinning

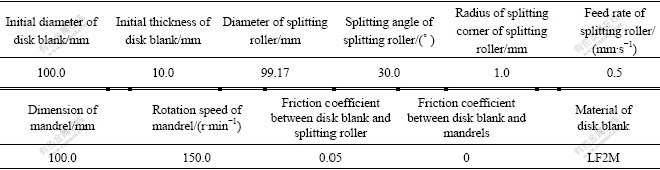
In order to verify the proposed model, the energy conversation principle and the comparison of splitting spinning force between experiment data and simulation results are adopted[13]. The simulation conditions are listed in Table 1.

Table 1 3D-FE simulation conditions of splitting spinning

2.2.1 Energy conversation verification

The energy definitions of ABAQUS software are used to verify the reliability of 3D-FE model, and ABAQUS offers the energy conversation principle. It is noted that, the 3D-FE model of splitting spinning is reliable if artificial strain energy (ALLAE) and kinetic energy (ALLKE) are much less than internal energy (ALLIE) during the splitting spinning process, as shown in Fig.5. At the beginning, due to the fact that the splitting roller hasn’t contacted disk blank, both artificial strain energy and internal energy are zero, whereas kinetic energy keeps a fixed value. Consequently, this indicates that the model is validated.

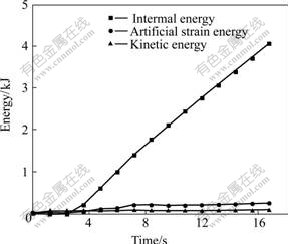
Fig.5 Energy transformation during splitting spinning process

2.2.2 Spinning force verification

The splitting spinning force is an important factor for understanding the forming mechanism and energy transformation. Therefore, experimental values[8] of spinning force (F_e) are compared with simulation values of spinning force (F_s), as shown in Table 2. From Table 2, it can be seen that there is a discrepancy between the simulation results of spinning force and the experimental results, however, its relative values are less than about 16.0%. This shows that the simulation results of spinning force are in good agreement with the experimental results, and the proposed model is validated.

Table 2 Comparison of splitting spinning force between F_e and F_s

2.3 Determination of calculation conditions

The material used in the 3D-FE model of splitting spinning is aluminum alloy, and its true properties[14] are listed in Table 3, and simulation conditions are the same as those in Table 1. The material properties of disk blank mainly lie in three material parameters, namely, yield stress σ_s, hardening exponent n and elastic modulus E, therefore, changing anyone of them will obtain various suppositional material with different material properties. Based on these procedures, the calculation conditions used in this study are determined as follows.

Table 3 True material properties of 3D-FE simulation of splitting spinning

Defining σ_s=70, 90, 110, 140, 170, 200 MPa as six valid numerical calculating data, remaining other parameters as listed in Table 1 and Table 3.

Defining n=0.05, 0.10, 0.16, 0.20, 0.25, 0.30, 0.35 as seven valid numerical calculating data, remaining other parameters as listed in Table 1 and Table 3.

Defining E=40, 60, 70, 80, 100, 130, 170 GPa as seven valid numerical calculating data, remaining other parameters as listed in Table 1 and Table 3.

3 Results and discussion

3.1 Force and power parameters

During the splitting spinning process, the force and power parameters mainly contain the splitting spinning force and the splitting spinning moment. The influences of material parameters σ_s, n, E on splitting spinning force and splitting spitting moment are shown in Fig.6 and Fig.7, respectively. From Fig.6, it can be seen that when σ_s or n or E increases, the splitting spinning force increases and depends mainly on n that ranges from 20 kN to 31 kN and E that ranges from 20 kN to 31 kN, then σ_s that ranges from 22 kN to 30 kN. From Fig.7, it can be seen that when σ_s or n or E increases, the splitting spinning moment increases and depends mainly on σ_s that ranges from 110 N?m to 195 N?m, then n that ranges from 125 N?m to 160 N?m and E that ranges from 120 N?m to 165 N?m. The reasons are that, the more the σ_s or n or E is, the more notable the strain-hardening is and the larger the resisting force of deformation is, and then the splitting spinning force and the splitting spinning moment increase obviously. Therefore, Fig.6 and Fig.7 provide a guide for selecting materials of disk blank and determining the equipments in terms of force and power parameters.

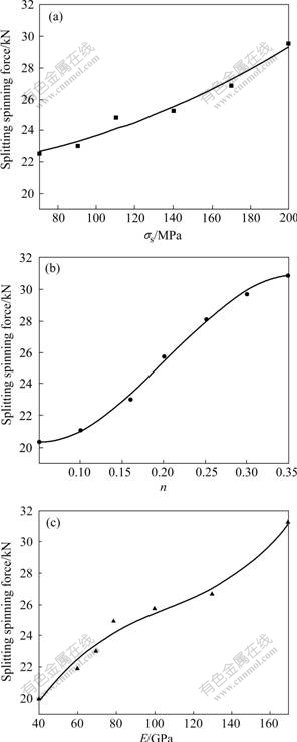
Fig.6 Influence laws of material parameters on splitting spinning force: (a) E=70 GPa, n=0.16; (b) E=70 GPa, σ_s=90 MPa; (c) n=0.16, σ_s=90 MPa

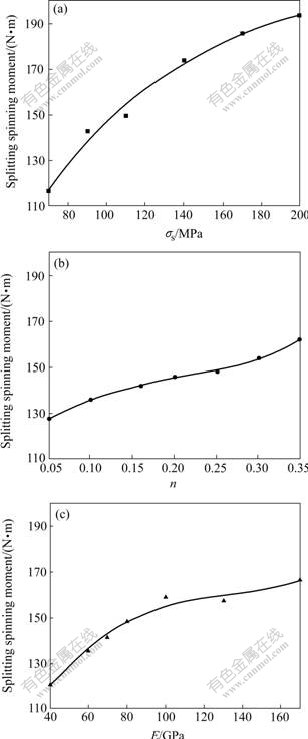
Fig.7 Influence laws of material parameters on splitting spinning moment: (a) E=70 GPa, n=0.16; (b) E=70 GPa, σ_s=90 MPa; (c) n=0.16, σ_s=90 MPa

3.2 Degree of inhomogeneous deformation

The degree of inhomogeneous deformation φ_id is defined as the difference between the maximum and the minimum equivalent plastic strain in the deformed blank, namely, φ_id=ε_max-ε_min. The larger the φ_id is, the more inhomogeneous the deformation of disk blank is, which may cause inner defects in the deformed blank. The influence of material parameters σ_s, n and E on φ_id is shown in Fig.8. From Fig.8, it can be seen that when σ_s or n decreases but E increases, the degree of inhomogeneous deformation φ_id of deformed blank increases, and the influence of E that ranges from 3.0 to 4.0 on φ_id is more notable, then σ_s that ranges from 3.1 to 3.3 and n that ranges from 3.0 to 3.4. The reasons are that, the less the σ_s or n is or the more the E is, the more difficult the elastic recovery of the deformed blank is and the more notable the strain-hardening is, and then the degree of inhomogeneous deformation φ_id increases obviously. Therefore, Fig.8 provides a guide for selecting materials of disk blank and predicting the forming limitation in terms of the degree of inhomogeneous deformation.

Fig.8 Influence laws of material parameters on degree of inhomogeneous deformation φ_id: (a) E=70 GPa, n=0.16; (b) E= 70 GPa, σ_s=90 MPa; (c) n=0.16, σ_s=90 MPa

3.3 Quality of flange

The quality of the deformed blank of splitting spinning is evaluated by the quality of flange. Thus, in this work, two judgments are provided, namely, the average thickness of flange 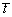 and the average deviation angle of flange[15]. The average thickness of flange is equal to the average thickness of four orthogonal directions in the radial direction of flange, reflecting the change of wall thickness from initial blank to deformed blank. The average deviation angle of flange is equal to the angle between the radial direction of flange and the horizontal direction, reflecting the degree of contact dies of flange, including average deviation angle of upper surface  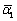and average deviation angle of lower surface .

3.3.1 Average thickness of flange

The influence of material parameters σ_s, n and E on average thickness of flange 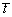 is shown in Fig.9. From Fig.9, it can be seen that when σ_s decreases but n or E increases, the average thickness of flange  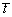increases, and the influence of n that ranges from 4.92 mm to 5.04 mm on  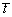are more notable, then σ_s that ranges from 4.95 mm to 5.04 mm and E that ranges from 4.98 mm to 5.04 mm. The reasons are that, the more the n or E is, the more the plastic strain is within the same forming time, and then the average thickness of flange  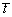increases obviously. The less the σ_s is, the more easily the blank turns into plastic deformation and the less the average thickness of flange is. Therefore, Fig.9 provides a guide for selecting materials of disk blank and determining the reduction of flange in terms of the average thickness of flange.

Fig.9 Influence laws of material parameters on average thickness of flange 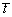: (a) E=70 GPa, n=0.16; (b) E=70 GPa, σ_s=90 MPa; (c) n=0.16, σ_s=90 MPa

3.3.2 Average deviation angle of flange

The influences of material parameters σ_s, n and E on average deviation angle of upper surface 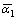 and average deviation angle of lower surface  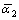are shown in Fig.10 and Fig.11, respectively. From Fig.10, it can be seen that when σ_s increases but n or E decreases, the average deviation angle of upper surface  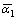increases, and the influence of n that ranges from 28.75? to 30.60? on  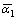is more notable, then σ_s that ranges from 30.00? to 30.60? and E that ranges from 29.50? to 30.40?. From Fig.11, it can be seen that when σ_s, or n or E decreases, the average deviation angle of that surface  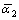increases, and the influence of n that ranges from 30.60? to 32.60? and E that ranges from 30.20? to 32.30? on  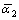is more notable, then σ_s that ranges from 31.40? to 32.25?. 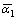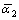The reasons are that, the more the n is, the less notable the strain-hardening is; meanwhile, the less E is, the more easily the surfaces of flange deviate from dies because of the elastic recovery of the blank, so that  or  increases obviously. The larger the σ_s is, the more easily the upper surfaces contact dies, so the more the  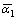is, the less the  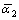is because of the elastic recovery of the blank from the uploading of splitting roller. Therefore, Fig.10 and Fig.11 provide a guide for selecting materials of disk blank and studying the over- deviation of flange in terms of the average thickness of flange.

Fig.10 Influence laws of material parameters on average deviation angle of upper surface : (a) E=70 GPa, n=0.16;   (b) E=70 GPa, σ_s=90 MPa; (c) n=0.16, σ_s=90 MPa

Fig.11 Influence laws of material parameters on average deviation angle of lower surface 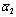: (a) E=70 GPa, n=0.16;  (b) E=70 GPa, σ_s=90 MPa; (c) n=0.16, σ_s=90 MPa

4 Conclusions

1) The slitting spinning force and the splitting spinning moment increase with the increase of yield stress, harden exponent and elastic modulus.

2) The degree of inhomogeneous deformation increases with the decrease of yield stress and hardening exponent and the increase of elastic modulus.

3) The average thickness of flange increases with the decrease of yield stress and the increase of harden exponent and elastic modulus.

4) The average deviation angle of upper surface increases with the increase of yield stress and the decrease of hardening exponent and elastic modulus; the average deviation angle of lower surface increases with the decrease of yield stress, hardening exponent and elastic modulus.

5) The corresponding variation ranges are given. The achievements may serve as an important guide for selecting the reasonable processing parameters of splitting spinning based on different aluminum alloys, and are very significant for optimum design and precision control of the splitting spinning process.

References

[1] WANG Cheng-he, LIU Ke-zhang. Spinning technology [M]. Beijing: China Machine Press, 1986. (in Chinese)

[2] YANG H, ZHAN M, LIU Y L, XIAN F J, SUN Z C, LIN Y, ZHANG X G. Some advanced plastic processing technologies and their numerical simulation [J]. Journal of Materials Processing Technology, 2004, 151(1/3): 63-69.

[3] WONG C C, DEAN T A, LIN J. A review of spinning, shear forming and flow forming process [J]. International Journal of Machine Tools & Manufacture, 2003, 43(14): 1419-1435.

[4] YANG He, GUO Liang-gang, ZHAN Mei, SUN Zhi-chao. Research on the influence of materials properties on cold ring rolling processes by 3D-FE numerical simulation [J]. Journal of Materials Processing Technology, 2006, 177(1/3): 634-638.

[5] GUO Liang-gang, YANG He, WU Yue-jiang, ZHAN Mei, LI Hong-wei. Research on influence of material parameters on cold ring rolling process [J]. Mechanical Science and Technology, 2005, 24(7): 839-843, 882. (in Chinese)

[6] FU Pei-fu, WANG Zhong-jin, HU Ping, LI Yun-xing. Numerical study for influences of material parameters on deformation of three-dimensional plastic compression of metal [J]. Journal of Jilin University of Technology, 1993, 23(4): 1-8. (in Chinese)

[7] XIE Xi, SUN Cheng-zhi, ZHANG Wei-gang. Study on the effect of material parameters and process parameters on the formability of rectangle box in sheet metal forming process [J]. Metal Forming Technology, 2003, 21(1): 41-43. (in Chinese)

[8] SCHMOECKEL D, HAUK S. Tooling and process control for splitting of disk blanks [J]. Journal of Materials Process Technology, 2000, 98(1): 65-69.

[9] HAUK S, VAZQUEZ V H, ALTAN T. Finite element simulation of the flow-splitting-process [J]. Journal of Materials Process Technology, 2000, 98(1): 70-80.

[10] YU Han-qing, CHEN Jin-de. The principle of metal plastic forming [M]. Beijing: China Machine Press, 1999. (in Chinese)

[11] ABAQUS, Inc. Getting Started with ABAQUS [M]. Version 6.4, 2004.

[12] ABAQUS, Inc. ABAQUS Analysis User’s Manual [M]. Version 6.4, 2004.

[13] GUO Liang-gang, YANG He, ZHAN Mei, LI Heng. 3D-FE modeling of cold ring rolling rrocess [C]// Proceedings of the sixth International Conference on Frontier of Design and Manufacturing. Xi’an, 2004: 625-626.

[14] WU Shi-chun, LI Miao-quan. Punching technology and die design [M]. Xi’an: Northwestern Polytechnical University Press, 2002. (in Chinese)

[15] ZHAN M, YANG H, ZHANG J H, XU Y L, MA F. 3D FEM analysis of influence of roller feed rate on forming force and quality of cone spinning [J]. Journal of Materials Processing Technology, 2007, 187/188: 486-491.

Foundation item: Projects(50405039, 50575186) supported by the National Natural Science Foundation of China; Project(50225518) supported by the National Science Foundation of China for Distinguished Young Scholars; Project supported by the Foundation of Northwestern Polytechnical University, China

Corresponding author: YANG He; Tel/Fax: +86-29-88495632; E-mail: yanghe@nwpu.edu.cn

(Edited by LI Xiang-qun)