J. Cent. South Univ. (2018) 25: 287-303

DOI: https://doi.org/10.1007/s11771-018-3737-4

A distributed dynamic mesh model of a helical gear pair with tooth profile errors

WANG Qi-bin(ÍõÆæ±ó)¹, MA Hong-bo(Âíºé²¨)¹, KONG Xian-guang(¿×Ïܹâ)¹, ZHANG Yi-min(ÕÅÒåÃñ)²

1. School of Electro-Mechanical Engineering, Xidian University, Xi¡¯an 710071, China;

2. School of Mechanical Engineering, Shenyang University of Chemical Technology,Shenyang 110819, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: A dynamic model of a helical gear rotor system is proposed. Firstly, a generally distributed dynamic model of a helical gear pair with tooth profile errors is developed. The gear mesh is represented by a pair of cylinders connected by a series of springs and the stiffness of each spring is equal to the effective mesh stiffness. Combining the gear dynamic model with the rotor-bearing system model, the gear-rotor-bearing dynamic model is developed. Then three cases are presented to analyze the dynamic responses of gear systems. The results reveal that the gear dynamic model is effective and advanced for general gear systems, narrow-faced gear, wide-faced gear and gear with tooth profile errors. Finally, the responses of an example helical gear system are also studied to demonstrate the influence of the lead crown reliefs and misalignments. The results show that both of the lead crown relief and misalignment soften the gear mesh stiffness and the responses of the gear system increase with the increasing lead crown reliefs and misalignments.

Key words: gear distributed dynamic model; tooth profile errors; helical gear pair; rotor system; dynamic response

Cite this article as: WANG Qi-bin, MA Hong-bo, KONG Xian-guang, ZHANG Yi-min. A distributed dynamic mesh model of a helical gear pair with tooth profile errors [J]. Journal of Central South University, 2018, 25(2): 287¨C303. DOI: https://doi.org/10.1007/s11771-018-3737-4.

1 Introduction

The helical gear transmission system is one of the most important and popular systems for motion and power transmission. Dynamic analysis is important and necessary in describing noise and durability characteristics of gear systems, and the special geometrical parameters of gears will influence the dynamic characteristics. Therefore, a relatively accurate dynamic model for prediction of vibration characteristics is necessary to analyze the vibration, noise and durability of gear systems, and to identify potential solutions to other problems.

Mesh stiffness and transmission error are the two important internal excitation sources of gear systems, which have attracted the attention of many researchers over the years [1¨C8]. In the simpler models, the gear mesh stiffness was assumed to be constant. In common models, a rectangular stiffness variation was used to represent a spur gear and a sinusoidal stiffness variation was used to represent a helical gear [9]. In recent years, more and more precise mesh stiffness models were established. WEBER [10] and YANG et al [11] proposed a model for calculating the mesh stiffness of a spur gear pair in which the tooth was considered a cantilever beam. In their model, the tooth stiffness was calculated by the potential energy method and the total stiffness of a gear pair included the bending stiffness, axial compressive stiffness and Hertzian contact stiffness. Based on WEBER and YANGs¡¯ work, CHEN et al [12, 13] established a mesh stiffness model of a spur gear pair with tooth profile modification and tooth root crack. MA et al [14, 15] and WAN et al [16] developed a mesh stiffness model taking the misalignment of gear root circle and base circle into account. For a helical gear pair, LI [17¨C19] and WEI et al [20] calculated the gear mesh stiffness and transmission error by the finite element method with manufacturing errors, assembly errors and the tooth profile modifications. Taking the load distribution non-uniform into account, WANG et al [21] presented an analytical mesh stiffness model using the thin slice theory. This model was effective for the tooth with tip relief, root relief, lead crown relief and misalignment. The effective mesh stiffness distribution had been proposed with tooth profile errors. From the above, more and more geometrical parameters are considered in analyzing the gear mesh stiffness.

Based on the existing literature on gear mesh stiffness excitation, many researchers studied the dynamic models of gear systems, and a comprehensive review of these models had been summarized in Ref. [22]. ANDERSSON et al [23] developed a classic torsional model of a gear pair in which the gear mesh stiffness was calculated by the finite element method. Most of the researches focused on flexural-torsional coupling gear dynamic models [24¨C29]. Free and forced vibration characteristics of spur and helical gears were analyzed using these models and the results revealed a strongly coupling between flexural and torsional vibrations. A group of studies [30¨C34] researched the dynamic characteristics of helical gear systems in which a twelve degrees of freedom dynamic model of the helical gear model was presented. The results showed the complex coupling amongst the transverse, torsional and axial motions of gears. NISHINO [35, 36] and ERITENEL et al [37, 38] presented an integrated model of a helical gear system. The gear mesh on the contact lines was reduced to two stiffnesses: a translational one and a twist one. VELEX et al [39] introduced a mathematical model for analyzing the gear dynamic characteristics with tooth profile errors. Each contact line on the action plane was discretized in independent elementary cells with constant stiffness. The stiffness was equal to a constant when the elementary cell is in contact; otherwise, it is equal to zero.

In most of the previous works, there is seldom researched on the gear dynamic characteristics by simulating the actual gear mesh process and using the actual gear mesh stiffness excitation. In fact, the gear mesh stiffness is softened by tooth profile errors. Therefore, the main objective of this study is to present a general dynamic model of a gear system in which the gear mesh can be represented by a pair of cylinders connected by a series of springs and the stiffness of each spring is equal to the effective mesh stiffness of the sliced tooth pair based on our earlier work [21]. What¡¯s more, dynamic responses by the proposed method will be presented and compared to the common method in Ref. [33] to validate correctness and advancement of the proposed method. Finally, dynamic responses of a gear system are also analyzed to demonstrate the effects of the tooth profile deviations and assembly errors.

This work consists of four sections. Reviews on the gear mesh stiffness models and gear dynamic models are listed in introduction. In Section 2, a gear dynamic model of a gear system is presented. The gear mesh is approximated as a pair of cylinders connected by a series of springs. Shafts and bearing flexibility are included in the model as well. Then, section 3 validates the correctness and advancement of the proposed method and studies the effect of tooth shape deviations and assembly errors on dynamic responses. Finally, conclusions are drawn in section 4.

2 Theory

2.1 Basic theory

2.1.1 Instantaneous contact lines

Figure 1 shows the mesh behavior of a helical gear. The blue lines represent the contact lines under different mesh positions. The contact line of the pinion moves its operating location from the root of one end of the tooth face S to the tip of the other end E during the mesh process. Therefore, it is important to determine the instantaneous contact lines. A spur gear is in fact a special case of a helical gear when the helix angle becomes zero. So, a helical gear, shown in Figure 2, can be approximated as a series of spur gear slices whose face width is relatively small. The red dash lines represent the end faces of those sliced teeth. The instantaneous contact lines can be calculated by determining whether the sliced tooth pair is in mesh.

Figure 1 Mesh behavior of a helical gear

Figure 2 Sliced tooth model

The instantaneous pressure angle of each sliced tooth in mesh is different and can be calculated as follows:

                      (1)

where ¦Õ_1,n and ¦Õ_2,n (n=1, 2 represent the pinion and gear respectively) of each sliced tooth pair can be expressed as follows:

       (2)

                       (3)

where k is the tooth pair number in mesh simultaneously (k=1, ¡¤¡¤¡¤, Ceil(¦Å) for different tooth pairs and ¦Å is contact ratio of the helical gear pair. The Ceil function returns the value of a number rounded upwards to the nearest integer); a denotes the center distance of the gear pair; b_i is the coordinate of the sliced tooth along the axial direction and locates at the center of each slice; r_b1 and r_b2 are the base circle radii of the pinion and gear respectively; z₁ and z₂ are the numbers of the pinion and gear teeth respectively. ¦Õ₁₂ represents the transverse operating pressure angle of the gear pair; ¦Õ₀ denotes the instantaneous roll angle of the first pinion tooth in mesh at the center of the tooth (b_i=0).

                  (4)

here mod function returns the modulus after division of ¦¸₁t by 2¦Ð/z₁; ¦¸₁ is the rotating speed of the pinion; t is for time; ¦Õ_0b is the minimum of the ¦Õ₀ and can be expressed as follows:

                      (5)

where B is the face width of the gear; 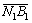is shown in Figure 3; ¦Â_b represents the base helix angle of the gear pair. Considering the hand of the pinion, helix angle ¦Â_b is defined as follows:

          (6)

As shown in Figure 3, when a sliced tooth pair i is in mesh, the instantaneous pressure angle must

Figure 3 Action line of a gear pair

be between the ¦Ó_b and ¦Ó_e. ¦Ó_b and ¦Ó_e are the minimum and maximum pressure angles of the gear pair, respectively, and can be written as follows:

               (7)

where is the theoretical action line of the gear pair; is the actual action line of the gear pair. By analyzing the instantaneous pressure angles of all the sliced tooth pairs, the contact lines can be determined. An example of contact lines of a helical gear pair is shown in Figure 4. It reveals that the contact lines vary under different mesh positions.

Figure 4 Contact lines of an ideal helical gear pair under different mesh positions [21]

2.1.2 Tooth profile errors

Tooth profile errors are separated into tooth profile modification, lead crown modification, misalignment and so on. The tooth profile modification has been studied in many researches [2, 3, 13]. So, the lead crown relief and misalignment are only studied in this work. The lead crown relief and misalignment will affect the mesh stiffness and transmission error excitations and further affect the vibration characteristics of a gear system.

Figure 5 shows a schematic of the infinitely expanded ridge curve. The lead crown relief is close to the curve defined by polynomial functions. Mesh stiffness and transmission error excitation model were developed in Ref. [21] by the lead crown relief.

Figure 5 Tooth lead crown relief

The misalignment error on the action plane is shown in Figure 6. The effective relative misalignment between the pinion and gear shafts was introduced in Ref. [21]. And the mesh stiffness and transmission error excitation model were also developed in Ref. [21] with the misalignment.

Figure 6 Misalignment error on action plane

2.2 Dynamic model

As shown in Figure 7, a coupled three- dimensional model of a helical gear rotor system is presented in this study. The system consists of shafts, flexible bearings and gears. Rotating shafts can be modeled as Timoshenko beams with effects of shear deformation and gyroscopic moment taken into account. The stiffness, mass and gyroscopic matrices of each beam element were given in Ref. [29]. The cross terms and the damping of the bearings are ignored. So, the rolling bearings are modeled as a stiffness form and the stiffness matrix was written in Ref. [34].

Figure 7 Model of a helical gear rotor system

2.2.1 Dynamic gear mesh model

In the common gear mesh models [33, 34], shown in Figure 8, the gears are connected to each other by a linear spring on the action plane (a plane tangent to both base cylinders). The motion equations in ¦È_x and ¦È_y directions only contain the gear mesh force component along the axial direction of gears (Fsin¦Â_b). In those models, it is assumed that the load distribution along the face width of a gear is uniform. So, the other gear mesh force component (Fcos¦Â_b) can be ignored.

Figure 8 A common gear mesh model

In fact, for the helical gear and gear with tooth profile errors, the load distribution along the face width of a gear is non-uniform. And a bigger flexural vibration in ¦È_x and ¦È_y directions may be caused by the non-uniform load distribution. Against the above problem and taking accurate force arms into account, a general distributed gear dynamic model is developed. As shown in Figure 9, the system is formed by the pinion and gear. The gear mesh can be represented by a pair of cylinders connected by a series of springs. a is the center distance of the gear pair. o₁ and o₂ denote the centers of the pinion and gear. ¦¸₁ and ¦¸₂ are the rotating speeds of the pinion and gear. r_b1 and r_b2 are the base circle radii of the pinion and gear, respectively. T₁ and T₂ are the torques applied to the pinion and gear, respectively. ¦Â_b represents the base helix angle and is defined in Eq. (6). A relative position angle ¦Á₁₂ (0¡Üa₁₂<2¦Ð) can be made by the line connecting the gear centers and the positive x-axis of the pinion.

With ¦Á₁₂ defined, the angle between the action plane and the positive y-axis becomes ¦×₁₂ (see Figure 9) and is defined as follows:

     (8)

where ¦Õ₁₂ represents the transverse operating pressure angle of the gear pair. is the effective mesh stiffness of each spring which is dependent on the gear mesh position and can be calculated as follows:

                              (9)

here k_i is the mesh stiffness of the spring i; kcf_i (0¡Ükcf_i¡Ü1) is the effective stiffness factor of the spring i and can be calculated by our earlier work [21], where the stiffness model is developed by the sliced method with the tooth profile errors.

Taking the influence of the rotating direction of the pinion into account, a sign function is introduced as follows:

Figure 9 Dynamic model of a helical gear pair:

            (10)

The displacement vector of a gear pair can be defined as follows:

(11)

where x, y, ¦È_x and ¦È_y represent the flexural degrees of freedom; z is the axial degree of freedom; ¦È_z is the torsional degree of freedom. With six degrees of freedom for each gear, the gear pair has a total of twelve degrees of freedom that define the coupling between the two shafts holding the gears. From the equilibriums of the force, flexural moment and torque for each gear, undamped equations of motion for a gear pair can be expressed as follows:

             (12a)

             (12b)

                (12c)

                  (12d)

                   (12e)

          (12f)

             (12g)

            (12h)

                (12i)

  (12j)

  (12k)

         (12l)

where N is the number of springs in mesh simultaneously; m₁ and m₂ are the masses of the pinion and gear, respectively; I₁ and I₂ represent the moments of inertia for the pinion and gear, respectively; J₁ and J₂ represent the polar moments of inertia for the pinion and gear, respectively; ¦Ó_i is the instantaneous pressure angle of each spring and can be calculated by Eq. (1); b_i and c_i of each spring are defined in Figure 9; l_i is the relative displacement of each spring in a direction normal to the tooth contact surface and is defined as follows:

 (13)

here, NLTE is no load transmission error which is a displacement excitation and given in Ref. [2].

Substituting Eq. (13) into Eq. (12), motion equations of a gear pair can be written in matrix form as follows:

                (14)

where the mass matrix of the gear pair is given as follows:

                         (15)

The mesh stiffness matrix of the gear pair can be expressed as follows:

                         (16)

where

     (17)

The external vectors of the gear pair are defined as follows:

(18)

                      (19)

Then, the instantaneous dynamic mesh force of each spring can be written as follows:

                               (20)

The dynamic mesh force of the gear pair is

                     (21)

2.2.2 Motion equations of a helical gear rotor system

The motion equation of system can be obtained by assembling equations of each component, and it can be expressed as follows:

                   (22)

where u is the state vector; F represents external force vector and is defined by Eqs. (18) and (19); M, C, G and K are the system mass, damping, gyroscopic and stiffness matrices, respectively. The total stiffness matrix of the system can be assembled by the way of Figure 10. Damping values of gear, bearing and shaft are not known in most cases even in the final stages of gear design. Therefore, for practical engineering purposes, the Rayleigh-type damping is used [34].

Figure 10 Schematic diagram of assembled stiffness matrix for a gear system

2.3 Solution

According to the previous theory, the dynamic model of a gear rotor system considering the effects of tooth profile errors and assembly errors can be developed by the Matlab software. A flow chart of the computational procedure for a specific rotational speed is shown in Figure 11. At the first step, the effective mesh stiffness distribution and no load transmission error are determined with tooth profile errors and assembly errors according to Ref. [21]. The second step is to develop the dynamic model of the gear rotor system using the effective mesh stiffness distribution and no load transmission error calculated in previous step. Then the motion equation of the system, Eq. (22), can be solved numerically by a Newmark-¦Â method. The whole process is repeated in the next time-step until the response converged. By analyzing the same gear rotor system for different rotational speeds, the structure dynamic responses can be detected.

3 Results and discussions

3.1 Simulation results

The purposes of this section are to analyze and compare the dynamic responses by the proposed gear dynamic model and the common gear dynamic model in Ref. [33]. Three cases are performed and the three cases use the same rotor system defined in Figure 7 and Tables 1¨C3. The gear parameters of the three cases are listed in Table 4. Case 1 is a narrow-faced helical gear rotor system with the face width B=16 mm. Case 2 is a wide-faced helical gear rotor system with the face width B=50 mm. Case 3 is a helical gear rotor system with tooth profile errors. The gear parameters are the same as case 2 and the parameters of tooth profile errors are listed in Table 2.

3.1.1 Case 1

Case 1 is a narrow-faced helical gear rotor system when the face width of the gear B=16 mm. The parameters of the system are defined in Tables 1¨C4. The error distribution and effective stiffness distribution are calculated by our earlier work [21]. And the results are shown in Figure 12. Each solid blue line in the waterfall diagram shows the instant error distribution and effective stiffness distribution along the contact line for a certain mesh position.

Figure 11 Simulation process

Table 1 Parameters of rotor system

Table 2 Lumped mass parameter

Table 3 Bearing parameter

Using the proposed gear dynamic model and the common dynamic model in Ref. [33] respectively, the dynamic responses of the gear rotor system are analyzed. Amplitude frequency responses of the pinion and gear in y, ¦È_x and ¦È_z directions by the two different methods are shown in Figure13. The resonance peaks of the pinion at 700, 1050, 1400, 2100, 2800, 4200, 5600 and 6600 r/min are evident from this figure. The resonance frequencies occur when the gear mesh frequency f_m is equal to f₁/2, f₃/2, f₁, f₃, 2f₁, 2f₃, 4f₁ and 2f₆. It reveals that the super-harmonic and sub-harmonic resonances may occur considering the effects of the time-varying mesh stiffness and no load transmission error by both the two methods.

Table 4 Gear parameters of three cases

Figure 12 Gear pair of case 1:

Figure 13 Dynamic responses of case 1:

As shown in Figure 13, the responses by two different models are very close except the response in ¦È_x direction of the gear. The results show that the proposed model is correct and both the two models are effective for dynamic analysis of a narrow-faced helical gear rotor system. In addition, the responses in ¦È_x direction have a big error between the two models. This is because shaft 2 is symmetric about the installation position of the gear and shaft 1 is asymmetric about the installation position of the pinion. Due to static deformations of the shafts, it is misalign between the pinion and gear and the gear engagement has the leaning load. The proposed model is useful for the gear pair with the leaning load and it cannot be considered in the model of Ref. [33].

In general, both the two models are effective for dynamic analysis of a narrow-faced helical gear rotor system.

3.1.2 Case 2

Case 2 is a wide-faced helical gear rotor system when the face width of the gear B=50 mm. The parameters of the system are defined in Tables 1¨C4. The error distribution and effective stiffness distribution are shown in Figure 14.

Using the proposed gear dynamic model and the common dynamic model in Ref. [33] respectively, the dynamic responses of the gear rotor system are analyzed. Amplitude frequency responses of the pinion and gear in y, ¦È_x and ¦È_z directions by the two different methods are shown in Figure 15. It also reveals that the super-harmonic and sub-harmonic resonances may occur considering the effects of the time-varying mesh stiffness and no load transmission error by both the two models. As shown in Figure 15, the responses by the two different models have a big error. This is because the proposed model incorporated non- uniform load distribution along contact line and the misalignment. And those factors could not be taken into account in the model of Ref. [33]. In general, for a wide-faced helical gear rotor system, the proposed model is effective and the model of Ref. [33] cannot predict accurately dynamic responses of a gear rotor system.

3.1.3 Case 3

Case 3 is a wide-faced helical gear rotor system with tooth profile errors. The parameters of the system are defined in Tables 1¨C3. The tooth profile error parameters are also listed in Table 4. The error distribution and effective stiffness distribution of the gear with tooth profile errors are analyzed by our earlier work [21] and the results are shown in Figure 16. Each solid blue line in the waterfall diagram shows the instant error distribution and effective stiffness distribution along the contact line for a certain mesh position. The tooth profile errors contain the tip relief, lead crown relief and misalignment. So, the error distribution and effective stiffness distribution are non-uniform.

Using the stiffness and error excitations with ideal tooth profile in Figure 14 and those with tooth profile errors in Figure 16, the dynamic responses of the gear rotor system with ideal tooth profile and tooth profile errors are analyzed respectively by the proposed gear dynamic model. Amplitude frequency responses of the pinion and gear in y, ¦È_x and ¦È_z directions by the ideal tooth profile and tooth profile errors are shown in Figure 17. The solid lines are the dynamic responses of the gear system with ideal tooth profile, and the dash lines are the dynamic responses of the gear system with tooth profile errors. In Figure 17, the dynamic responses by different tooth profile errors have a small error. But for an accurate dynamic analysis of a gear system, the tooth profile errors should be included.

Figure 14 Gear pair of case 2:

Figure 15 Dynamic responses of case 2:

Figure 16 Gear pair of case 3:

Figure 17 Dynamic responses of case 3:

As explained above, the results show that the proposed dynamic model is effective and advanced for general gear systems, narrow-faced gear, wide-faced gear and gear with tooth profile errors. Especially for the wide-faced gear and gear with tooth profile errors, the proposed model is more accurate than the model in Ref. [33] for dynamic analysis.

3.2 Influence of some parameters

In the previous section, it is demonstrated that the model is effective and advanced for dynamic analysis of gear rotor systems. In this section, parametric studies are performed for several design parameters in order to study their influence on the overall behavior of the gear rotor system. The helical gear rotor system, case 2 in section 3.1, is used to predict the dynamic responses.

3.2.1 Influence of the lead crown relief

Using the proposed method, the effective stiffness distribution and dynamic responses of the gear system are analyzed with various lead crown relief C_¦Â=0, 20, 40, 60 ¦Ìm on both the pinion and gear. Figure 18 shows the effective stiffness distribution while C_¦Â=0 and C_¦Â=40 ¦Ìm. Each line in the waterfall diagram shows the instant effective stiffness distribution for a certain mesh position. Figure 18(a) shows the stiffness distribution of the gear with ideal tooth profile. As shown in Figure 18(b), there is partial effective stiffness equal to zero because parts of the tooth surface are out of contact. The mesh deformation is not large enough to compensate for the separation from the tooth profile errors due to the lead crown relief. In addition, due to static deformation of the shafts, the stiffness distribution is asymmetric along face width.

In Figure 19, dynamic responses of the pinion and gear in different directions are plotted against the input speed for different lead crown reliefs. It reveals that the super-harmonic and sub-harmonic resonances occur considering the time-varying mesh stiffness and no load transmission error excitations. The responses increase with the increasing lead crown reliefs. This is because the lead crown relief softens the gear mesh stiffness. For vibration and noise-deduction, the lead crown relief is expected as small as possible. But the small lead crown relief may lead to edge contact and stress concentration. Therefore, in some practical design cases, a tradeoff should be made between the vibration and edge contact by applying the lead crown relief.

Figure 18 Effective stiffness distributions under different lead crown reliefs:

Figure 19 Dynamic responses of pinion and gear under different lead crown reliefs:

3.2.2 Influence of misalignment

In this section, the influence of the misalignment on dynamic responses is studied. Effective stiffness distribution and dynamic responses of the helical gear rotor system, case 2 in Table 4, are analyzed when the gear pair has the misalignment errors of the pinion shaft. Figure 20 shows effective stiffness distributions when the misalignment ¦È_x1=0¡ã and ¦È_x1=0.06¡ã. Each line in the waterfall diagram shows the instant effective stiffness distribution for a certain mesh position. Due to static deformation of the shafts, it is misalign between the pinion and gear. Figure 20(a) shows the stiffness distribution of the gear with ideal tooth profile. In Figure 20(b), there is partial effective stiffness equal to zero due to the misalignment. This is because tooth contact patterns have been changed by the misalignment. Since tooth side heavier contacts make the tooth loads concentrate on one of the tooth side and the other tooth side is separate due to the misalignment.

Figure 21 shows dynamic responses of the pinion and gear in different directions for the different misalignments. It reveals that the dynamic responses become larger when the misalignment errors of the gear become greater. This is because the misalignment softens the gear mesh stiffness. In addition, the misalignment leads to edge contact and stress concentration on the tooth side. In summary, the misalignment is harmful to not only the vibration but also contact stress. Therefore, in some practical design cases, the misalignment should try to be avoided in the gear rotor system.

4 Conclusions

A dynamic model of a helical gear rotor system is developed in this work. Then the dynamic responses are analyzed by the proposed method. The conclusions drawn from the study may be summarized as follows:

1) A distributed dynamic model of a helical gear pair is developed with tooth profile errors. The gear mesh is represented by a pair of cylinders connected by a series of springs and the stiffness of each spring is equal to the effective mesh stiffness. The model has the capability of including some relevant parameters, such as tooth profile errors, misalignment, pressure angle, helical angle, installation angle, face width of a gear and rotating direction of the gear. Then three cases are presented to analyze the dynamic responses of gear rotor systems. The results show that the model is effective and advanced for general gear rotor systems, narrow-faced gear, wide-faced gear and gear with tooth profile errors. Especially for the wide-faced gear pair and gear with tooth profile errors, the proposed model is more accurate for dynamic analysis.

2) The effects of the lead crown reliefs and misalignments on the dynamic responses of a helical gear rotor system are also studied. It reveals that the super-harmonic and sub-harmonic resonances may occur considering the time-varying mesh stiffness and no load transmission error excitations. Both of the lead crown relief and misalignment soften the gear mesh stiffness. The responses of the gear increase with the increasing lead crown reliefs and misalignments of the gear. In addition, a tradeoff should be made between the vibration and edge contact by applying the lead crown relief. And the misalignment should try to be avoided in the gear rotor system.

Figure 20 Effective stiffness distributions under different misalignments:

Figure 21 Dynamic responses of pinion and gear under different misalignments:

Nomenclature

a

Center distance of the gear pair

b_i

Coordinate of the sliced tooth along the axial direction

B

Face width of a gear

Length of the actual action line of the gear pair

F₁₂, F_e

External force vectors of the gear pair

Mesh force of the sliced tooth pair i

F_m

Instantaneous dynamic mesh force of the gear pair

kcf_i

The effective stiffness factor of the sliced tooth pair i

k_i

Mesh stiffness of the sliced tooth pair i

The effective stiffness of the sliced tooth pair i

K₁₂

Mesh stiffness matrix of the gear pair

l_i

The relative displacement of each spring in a direction normal to teeth contact surfaces

M₁₂

Mass matrix of the gear pair

NLTE

The no-load transmission error

N

Number of springs in mesh simultaneously

Length of the theoretical action line of the gear pair

r_b1, r_b2

Base circle radii of the pinion and gear, respectively

T₁, T₂

Torques applied to the pinion and gear, respectively

z₁, z₂

Numbers of the pinion and gear teeth, respectively

¦Á₁₂

The relative position angle of the gears

¦Â_b

Base helix angle of the gear pair

¦Å

Contact ratio of the gear pair

¦Ó_b

The minimum pressure angle of the gear pair in mesh

¦Ó_e

The maximum pressure angle of the gear pair in mesh

¦Ó_i

Instantaneous pressure angle of the sliced tooth i

¦Õ₁₂

Transverse operating pressure angle of the gear pair

¦¸₁, ¦¸₂

Rotating speeds of the pinion and gear, respectively

References

[1] PALERMO A, MUNDO D, HADJIT R, DESMET W. Multibody element for spur and helical gear meshing based on detailed three-dimensional contact calculations [J]. Mechanism and Machine Theory, 2013, 62: 13¨C30. DOI: 10.1016/j.mechmachtheory.2012.11.006.

[2] VELEX P, AJMI M. On the modelling of excitations in geared systems by transmission errors [J]. Journal of Sound and Vibration, 2006, 290(3): 882¨C909. DOI: 10.1016/j.jsv.2005. 04.033.

[3] MOHAMAD E N, KOMORI M, MURAKAMI H, KUBO A, FANG S. Analysis of general characteristics of transmission error of gears with convex modification of tooth flank form considering elastic deformation under load [J]. Journal of Mechanical Design, 2009, 131(6): 1¨C9. DOI: 10.1115/ 1.3116261.

[4] VELEX P, AJMI M. Dynamic tooth loads and quasi-static transmission errors in helical gears¡ªApproximate dynamic factor formulae [J]. Mechanism and Machine Theory, 2007, 42(11): 1512¨C1526. DOI: 10.1016/j.mechmachtheory.2006. 12.009.

[5] VELEX P, BRUYERE J, HOUSER D R. Some analytical results on transmission errors in narrow-faced spur and helical gears: influence of profile modifications [J]. Journal of Mechanical Design, 2011, 133(3): 031010. DOI: 10.1115/ 1.4003578.

[6] MUNRO R. A review of the theory and measurement of gear transmission error [J]. Proceedings of the First IMechE Conference on Gearbox Noise and Vibration (Paper c404/032). 1990: 3¨C10.

[7] MUNRO R, PALMER D, MORRISH L. An experimental method to measure gear tooth stiffness throughout and beyond the path of contact [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2001, 215(7): 793¨C803.

[8] WANG Qi-bin, ZHAO Bo, FU Yang, KONG Xian-guang, MA Hui. An improved time-varying mesh stiffness model for helical gear pairs considering axial mesh force component [J]. Mechanical Systems and Signal Processing, 2018. https://doi.org/ 10.1016/j.ymssp.2018.01.012.

[9] MATSUHISA H, MIYAJI Y, SATO S. Parametrically excited vibration with external constant load and damping [J]. Memoirs of the Faculty of Engineering, Kyoto Univ, 1982, 44: 158¨C167.

[10] WEBER C. The deformation of loaded gears and the effect on their load-carrying capacity. Part 3 [M]. Dept. of Scientific and Industrial Research, Sponsored Research, Germany, 1949.

[11] YANG D C H, LIN J. Hertzian damping, tooth friction and bending elasticity in gear impact dynamics [J]. Journal of Mechanisms, Transmissions, and Automation in Design, 1987, 109(2): 189¨C196.

[12] CHEN Zai-gang, SHAO Yi-min. Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth [J]. Engineering Failure Analysis, 2011, 18(8): 2149¨C2164. http://dx.doi.org/10.1016/j.engfailanal.2011.07. 006.

[13] CHEN Zai-gang, SHAO Yi-min. Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack [J]. Mechanism and Machine Theory, 2013, 62: 63¨C74. DOI: http://dx.doi.org/10.1016/j.mechmachtheory. 2012.10.012.

[14] MA Hui, SONG Rong-ze, PANG Xu, ZENG Jin, WEN Bang-chun. Time-varying mesh stiffness calculation of cracked spur gears [J]. Engineering Failure Analysis, 2014, 44: 179¨C194. DOI: 10.1016/j.engfailanal.2014.05.018.

[15] MA Hui, PANG Xu, FENG Ran-jiao, HE Wang-peng, HE Zhen-jia. Improved time-varying mesh stiffness model of cracked spur gears [J]. Engineering Failure Analysis, 2015, 55: 271¨C287. DOI: 10.1016/j.engfailanal.2015.06.007.

[16] WAN Zhi-guo, CAO Hong-rui, ZI Yan-yang, HE Wang-peng, HE Zheng-jia. An improved time-varying mesh stiffness algorithm and dynamic modeling of gear-rotor system with tooth root crack [J]. Engineering Failure Analysis, 2014, 42: 157¨C177. DOI: 10.1016/j.engfailanal.2014.04.005.

[17] LI S. Effects of machining errors, assembly errors and tooth modifications on loading capacity, load-sharing ratio and transmission error of a pair of spur gears [J]. Mechanism and Machine Theory, 2007, 42(6): 698¨C726. DOI: http://dx.doi. org/10.1016/j.mechmachtheory.2006.06.002.

[18] LI S. Effect of addendum on contact strength, bending strength and basic performance parameters of a pair of spur gears [J]. Mechanism and Machine Theory, 2008, 43(12): 1557¨C1584.

[19] LI S. Effects of misalignment error, tooth modifications and transmitted torque on tooth engagements of a pair of spur gears [J]. Mechanism and Machine Theory, 2015, 83: 125¨C136. DOI: http://dx.doi.org/10.1016/j.mechmachtheory. 2014.09.011.

[20] WEI Jing, SUN Wei, WANG Li-cun. Effects of flank deviation on load distributions for helical gear [J]. Journal of Mechanical Science and Technology, 2011, 25(7): 1781¨C1789. DOI: 10.1007/s12206-011-0416-x.

[21] WANG Qi-bin, ZHANG Yi-min. A model for analyzing stiffness and stress in a helical gear pair with tooth profile errors [J]. Journal of Vibration and Control, 2017, 23(2): 272¨C289. DOI: 10.1177/1077546315576828.

[22] VELEX P. On the modelling of spur and helical gear dynamic behaviour [M]. ArXiv preprint, 2012, arXiv:1204.2636.

[23] ANDERSSON A, VEDMAR L. A dynamic model to determine vibrations in involute helical gears [J]. Journal of Sound and Vibration, 2003, 260(2): 195¨C212. DOI: 10.1016/ s0022-460x(02)00920-3.

[24] IIDA H, TAMURA A, KIKUCH K, AGATA H. Coupled torsional-flexural vibration of a shaft in a geared system of rotros-1 [J]. Bulletin of the JSME, 1980, 23(186): 2111¨C2117.

[25] HUANG Guan-hui, XU Si-si, ZHANG Wei-hua, YANG Cai-jin. Super-harmonic resonance of gear transmission system under stick-slip vibration in high-speed train [J]. Journal of Central South University, 2017, 24(3): 726¨C735. DOI: 10.1007/s11771-017-3474-0.

[26] CHOI S T, MAU S Y. Dynamic analysis of geared rotor-bearing systems by the transfer matrix method [J]. Journal of Mechanical Design, 2001, 123(4): 562¨C568.

[27] LEE A S, HA J W, CHOI D H. Coupled lateral and torsional vibration characteristics of a speed increasing geared rotor-bearing system [J]. Journal of Sound and Vibration, 2003, 263(4): 725¨C42. DOI: 10.1016/s0022- 460x(02)01103-3.

[28] CUI Ya-hui, LIU Zhan-sheng, WANG Yong-liang, YE Jian-huai. Nonlinear dynamic of a geared rotor system with nonlinear oil film force and nonlinear mesh force [J]. Journal of Vibration and Acoustics, 2012, 134(4): 041001.

[29] MA Hui, FENG Ran-jiao, PANG Xu, SONG Rong-zen, WEN Bang-chun. Effects of tooth crack on vibration responses of a profile shifted gear rotor system [J]. Journal of Mechanical Science and Technology, 2015, 29(10): 4093¨C4104. DOI: 10.1007/s12206-015- 0903-6.

[30] KAHRAMAN A. Effect of axial vibrations on the dynamics of a helical gear pair [J]. Journal of Vibration and Acoustics, 1993, 115(1): 33¨C39.

[31] BLANKENSHIP G W, SINGH R. Dynamic force transmissibility in helical gear pairs [J]. Mechanism and Machine Theory, 1995, 30(3): 323¨C339. DOI: 10.1016/0094- 114x(94)00048-p.

[32] BLANKENSHIP G W, SINGH R. A new gear mesh interface dynamic model to predict multi-dimensional force coupling and excitation [J]. Mechanism and Machine Theory, 1995, 30(1): 43¨C57. DOI: 10.1016/0094-114x(94)00018-g.

[33] KUBUR M, KAHRAMAN A, ZINI D M, KIENILE K. Dynamic analysis of a multi-shaft helical gear transmission by finite elements: Model and experiment [J]. Journal of Vibration and Acoustics, Transactions of the ASME, 2004, 126(3): 398¨C406. DOI: 10.1115/1.1760561.

[34] ZHANG Yi-min, WANG Qi-bin, MA Hui, HUANG Jin, ZHAO Chun-yu. Dynamic analysis of three-dimensional helical geared rotor system with geometric eccentricity [J]. Journal of Mechanical Science and Technology, 2013, 27(11): 3231¨C3242. DOI: 10.1007/s12206-013-0846-8.

[35] NISHINO T. Vibration analysis of the helical gear system using the integrated excitation model [J]. Journal of Advanced Mechanical Design Systems and Manufacturing, 2007, 1(4): 541¨C552. DOI: 10.1299/jamdsm.1.541.

[36] NISHINO T. Integrated excitation models of the helical gear system [J]. ASME 2007 International Design Engineering Technical Conference and Computers and Information in Engineering Conference. American Society of Mechanical Engineers, 2007: 477¨C486.

[37] ERITENEL T, PARKER R G. An investigation of tooth mesh nonlinearity and partial contact loss in gear pairs using a lumped-parameter model [J]. Mechanism and Machine Theory, 2012, 56: 28¨C51. DOI: 10.1016/j.mechmachtheory. 2012.05.002.

[38] ERITENEL T, PARKER R G. Three-dimensional nonlinear vibration of gear pairs [J]. Journal of Sound and Vibration, 2012, 331(15): 3628¨C3648. DOI: 10.1016/j.jsv.2012.03.019.

[39] VELEX P, MAATAR M. A mathematical model for analyzing the influence of shape deviations and mounting errors on gear dynamic behaviour [J]. Journal of Sound and Vibration, 1996, 191(5): 629¨C660. DOI: 10.1006/jsvi.1996. 0148.

(Edited by YANG Hua)

ÖÐÎĵ¼¶Á

Îó²î³ÝÀªÐ±³ÝÂÖ·Ö²¼Ê½ÄöºÏ¶¯Á¦Ñ§Ä£ÐÍ

ÕªÒª£º±¾ÎÄÑо¿ÁËб³ÝÂÖת×Óϵͳ¶¯Á¦Ñ§Ä£ÐÍ¡£Ê×ÏÈ£¬½«Ð±³ÝÂÖÄöºÏµÈЧΪÑØ³Ý¿í·½ÏòÉÏ·Ö²¼µÄһϵÁв¢Áªµ¯»ÉÏàÁ¬µÄÔ²Öù£¬ÆäÖе¯»ÉµÄ¸Õ¶ÈΪ³ÝÂÖµÈЧÄöºÏ¸Õ¶È£¬½¨Á¢Îó²î³ÝÀªÐ±³ÝÂÖ·Ö²¼Ê½¶¯Á¦Ñ§Ä£ÐÍ¡£½øÒ»²½½áºÏת×Ó¨CÖá³Ð¶¯Á¦Ñ§Ä£ÐÍ£¬½¨Á¢³ÝÂÖ¨Cת×Ó¨CÖá³Ðϵͳ¶¯Á¦Ñ§Ä£ÐÍ¡£È»ºó£¬Í¨¹ý3¸öËãÀý·ÖÎöÁ˳ÝÂÖϵͳµÄ¶¯Á¦Ñ§ÏìÓ¦£¬½á¹ûÏÔʾ£¬¶ÔÓÚÕ­³ÝÃæ³ÝÂÖ¡¢¿í³ÝÃæ³ÝÂÖ¡¢ÐÞÐγÝÀª³ÝÂÖ£¬±¾ÎĵĶ¯Á¦Ñ§Ä£Ð;ùÊÇÓÐЧµÄ¡£×îºó£¬·ÖÎöÁ˳ÝÏòÐÞÐκͳÝÂÖ²»¶ÔÖжԳÝÂÖϵͳ¶¯Á¦Ñ§ÏìÓ¦µÄÓ°Ï죬½á¹û±íÃ÷£¬³ÝÏòÐÞÐκͳÝÂÖ²»¶ÔÖÐʹµÃ³ÝÂֵĸնȱäС¡¢³ÝÂÖϵͳµÄÕñ¶¯ÏìÓ¦±ä´ó¡£

¹Ø¼ü´Ê£º·Ö²¼Ê½¶¯Á¦Ñ§Ä£ÐÍ£»³ÝÀªÎó²î£»Ð±³ÝÂÖ£»×ª×Óϵͳ£»¶¯Á¦Ñ§ÏìÓ¦

Foundation item: Projects(51605361, 51505357) supported by the National Natural Science Foundation of China; Projects(XJS16041, JB160411) supported by the Fundamental Research Funds for the Central Universities, China

Received date: 2016-04-26; Accepted date: 2017-12-01

Corresponding author: WANG Qi-bin, PhD, Lecturer; Tel: +86-29-88203115; E-mail: qbwangpap@163.com; ORCID: 0000-0003- 4686-5336