水平推力作用下抗滑桩间土拱效应影响因素的数值分析

刘钦^{1, 2}，李地元³，刘志祥³，刘静⁴

(1. 北京科技大学 土木与环境工程学院，北京，100083；

2. 山东黄金集团 三山岛金矿，山东 莱州，261442；

3. 中南大学 资源与安全工程学院，湖南 长沙，410083；

4. 中南大学 土木工程学院，湖南 长沙，410075)

摘要：利用FLAC^3D软件对抗滑桩后土体的应力拱产生过程和形成机理进行三维数值分析，并通过一系列的对比计算，研究桩间距、土体性质(包括土体的内摩擦角、黏聚力、弹性模量、泊松比、膨胀角)以及桩土接触面性质等因素对土拱效应的影响。研究结果表明：随着抗滑桩桩间距的增大，土拱范围变小，土拱形状也由拱形发展到扁平抛物线形，桩的荷载分担比降低。土体内摩擦角、土体黏聚力以及桩土之间的相对弹性模量对土拱效应的影响呈正相长关系，而土体的泊松比对桩后土拱范围的影响呈反比关系，土体的膨胀角对土拱效应影响不太明显；随着桩土接触面的粗糙程度增加，桩后土拱的范围增大，土拱效应也越显著。

关键词：水平推力；土拱效应；抗滑桩；应力拱；桩土相互作用

中图分类号：TU473          文献标志码：A         文章编号：1672-7207(2011)07-2071-07

Numerical analysis of influence factors on soil arching effect between anti-sliding piles under horizontal pushing loads

LIU Qin^{1, 2}, LI Di-yuan³, LIU Zhi-xiang³, LIU Jing⁴

(1. School of Civil and Environment Engineering, University of Science & Technology Beijing, Beijing 100083, China;

2. Sanshandao Gold Mine, Shandong Gold Group Co. Ltd., Laizhou 261442, China;

3. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

4. School of Civil Engineering, Central South University, Changsha 410075, China)

Abstract: Through 3D numerical analysis of the arching effect between anti-slide piles and soils by FLAC^3D­­ software, the process and the mechanism of stress arching effect in the soil were studied. By a series of calculations and comparisons, the influence factors on the soil arching effect were determined. For instance, the space of piles, the mechanical properties of soil (such as internal frictional angle, cohesion, elastic modulus, Poison’s ratio and dilation angle of soil) and the interface properties between piles and soils were analyzed in detail. The results show that the soil arch zone will become small and the arch shape will change from arched to parabola with the increase of pile spaces. The internal friction angle, the cohesion and the relative elastic modulus between piles and soil play a positive role in soil arching effects, but the Poisson’s ratio plays a negative role. The shear dilation angle has no conspicuous effect on the soil arching. Besides, the soil arch zone will enlarge with the increase of roughness of contact interface between piles and soils.

Key words: horizontal pushing load; soil arching effect; anti-slide pile; stress arch; interaction between pile and soil

1943年Terzagh通过著名的活动门试验，证实了土力学领域土拱效应的存在，并且称这种由于介质的不均匀移动导致介质应力状态发生改变，引起应力重新分配，将荷载从屈服土体转移至附近刚性边界的现象称为土拱效应^[1]。之后，Ladanyi等^[2-4]借助数值模拟和理论研究的方法对“活动门”试验的结果进行了广泛和深入的研究。Wang等^[5]考虑土拱效应来设计抗滑桩，提出了极限桩间距的存在；Richard^[6]提出土拱拱形近似悬链线的小主应力轨迹；Bosscher等^[7]通过室内模型试验模拟了砂性土边坡中的土拱效应；Kellogg^[8]研究发现土拱形状有三角形、抛物线形、半球形、圆顶形等；Park等^[9]假定小主应力为圆弧，对挡土墙后土拱效应进行了分析。在国内，不少学者采用现场试验、理论和数值分析等多种方法对土拱效应进行了研究^[10-13]，同时，一些学者将土拱理论应用于工程实际，取得了良好的效果^[14-16]。目前，由于试验条件等许多客观原因，土拱理论研究中，尤其是抗滑桩后的土拱效应仍存在一些值得探讨的问题，如桩后土拱效应产生的机理，土拱产生的过程、条件及其影响因素，拱形及拱体的几何参数和拱体的微观特性等。本文作者针对上述问题建立抗滑桩与桩周土的力学模型, 采用连续介质快速拉格朗日有限差分法，利用FLAC^3D软件模拟桩后土拱产生的过程、条件及影响因素，分析抗滑桩后土拱效应的产生机理，分析了桩间距、土体性质(包括土体内摩擦角、黏聚力、弹性模量、泊松比等)、桩土接触面性质等因素对土拱效应的影响。

1  计算模型及基本算例

1.1  基本计算模型

取一定厚度的桩土体作为分析对象，其平面俯视图如图1(a)所示。抗滑桩桩径为d，桩间中心距为s，桩长为h，土体为均质土层，在桩土之间设置无厚度的接触面单元，排桩的前后计算区域均取为10d，以减少边界效应对模型的影响。模型的边界约束条件为：对称边界采用 y 方向全约束, 前侧边界采用x 向约束，桩底固定, 桩顶自由, 有限差分的网格划分如图 1(b)所示。滑坡推力采用在土体侧面施加均布荷载, 模拟滑坡推力使土体和桩发生侧向运动。模型计算至最大不平衡力达到一个相对较小的值，若最大不平衡力比率为10^-5，则计算终止，认为模型内部应力重分布完成。

图1  桩土体在滑坡推力作用下的基本计算模型

Fig.1  Basic calculation model of piles and soil under horizontal pushing loads

1.2  桩土体的本构关系

与土体相比，桩体的强度和弹性模量都要大得多，故文中桩单元采用线弹性模型，土体单元采用Mohr-Coulomb弹塑性模型的组合破坏准则，即拉伸载荷作用下的张拉破坏和压缩载荷作用下的剪切破坏准则。张拉破坏准则为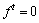，屈服方程为：

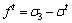                (1)

式中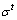：为土体的张拉强度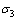；为最小主应力。剪切破坏准则为，屈服方程为：

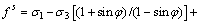
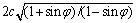          (2)

式中：c和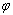分别为土体的黏聚力和内摩擦角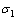；和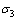分别为最大和最小主应力。

1.3  桩土接触单元特性

FLAC^3D软件里设置了一种由3节点组成的三角形接触单元。在每一个计算时步里，接触目标面和接触点的法向绝对侵入量和切向相对速度都被计算出来，将这2个值代入接触面本构方程就可以计算出接触面法向应力矢量和切向应力矢量。接触面单元服从库仑剪切破坏屈服准则和拉破坏屈服准则。接触面法向力和切向力的本构方程为：

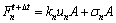            (3)

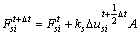         (4)

式中：k_n为法向接触面刚度；k_s为切向接触面刚度；A为接触面面积。

1.4  基本算例及其结果

基本算例中取抗滑桩桩径d=1 m，桩间中心距为L=4d，桩长为h=10 m，土体为均质土层，桩土体的计算参数见表1，接触面单元的法向刚度k_n和切向刚度k_s均为1×10⁷ kN/m，桩后均布载荷为50 kPa/m。通过计算得到图2所示的土体最大x方向应力σ_x矢量图以及x方向应力等值线图。

表1  基本数值算例中桩土体的力学参数

Table 1  Mechanical parameters of piles and soil in basic numerical model

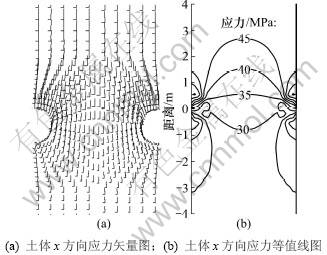
图2  基本算例中土体的最大主应力矢量图和等值线图

Fig.2  Vector and contour diagram of maximum principal stress in soil from basic numerical model

从图2可以看到2种形式的应力拱：(1) 在桩后外力的作用下，由于抗滑桩对土体的约束，导致桩后土体的主应力发生了旋转，最大主应力方向指向并垂直桩表面，最大主应力方向的连线呈半椭圆形拱形，在抗滑桩后的土层中形成了一个明显的应力拱，应力在桩后达到最大，桩前土体应力最小，说明荷载通过土拱传递到桩体；(2) 在桩间由于桩内侧与土体的摩擦，对土体产生一定的拖曳作用，也导致桩间土体的主应力发生了旋转，在桩间至桩前土体中出现微弱反方向的应力拱。

图3所示为土体中一些关键剖面线上的应力分量变化情况。从图3(a)可见：2桩中轴线上各点上的应力σ_y，在离抗滑桩较远的土体中变化不大，在桩后2~ 3 m处开始增大，到桩后1 m处达到最大，在桩间σ_y开始急剧变小，在桩前1 m处达到最小，随后略有增加，最终在桩前保持稳定。在图3(b)可见：桩后3 m的土体应力σ_x分布均匀，越靠近桩身处，在桩后的σ_x急剧增大，而桩间土体承担的σ_x变得较小，整个分布曲线呈下凹的拱形。桩前土体的σ_x比桩后土体的小，呈现一定幅度上凸的曲线。以上应力分布曲线说明在桩后3 m左右开始形成土拱，土体中的应力以应力拱形的方式将一部分载荷传递到桩身。

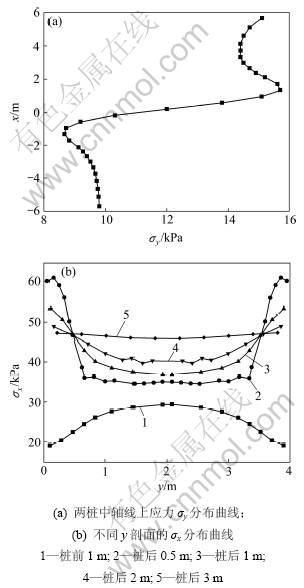
图3  基本算例中土体关键剖面的应力分量变化趋势

Fig.3  Variation of stress components along some critical lines in basic numerical model

引入桩的荷载分担比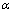，令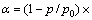 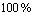，其中，p为桩前残余荷载；p₀为总荷载。从图3(b)可以计算出桩的荷载分担比。图3(b)中将各曲线与水平轴之间所围成的面积即为各曲线所在剖面的等效截面所承担的荷载。经计算，该基本算例中桩前土体承受的荷载约为96 kPa，而总荷载为200 kPa，故桩的荷载承担比为52%。

2  桩间距对土拱效应的影响分析

在基本算例的基础上，对桩间距与桩径之比s/d分别等于2，6，8，10和12时的模型进行计算。图4所示为s/d=2和8时桩前和桩后一些关键剖面上的应力分量σ_x分布曲线图，图5所示为不同桩间距条件下2桩中轴线截面上各点的y方向应力分布曲线图。

对不同桩间距对土拱效应的分析可见：桩间距对土拱效应的影响很大，随着桩间距的增大，土拱范围变小，土拱形状也由拱形发展到扁平抛物线形，当  s/d＞8时，土拱基本已不存在。当s/d=2，4，6时，中轴线上的σ_y有明显变化，在x=-2~3 m范围内出现2个明显的拱形，而s/d＞8后，中轴线上的σ_y为微弯的曲线，拱效应已不明显。可见，随着桩间距的增大，土拱效应会逐渐减弱，桩的荷载分担比也逐渐降低。这也验证了极限桩间距的存在，可认为极限桩间距为s=8d。

3  土体性质对土拱效应的影响分析

3.1  内摩擦角的影响

在基本算例中其他参数不变的情况下，分别对土体在内摩擦角φ=0°，10°，20°，40°等情况下进行计算，根据计算结果得到了土体在不同内摩擦角下桩中线各点的y方向应力曲线，如图6所示。从图6可见：随着土体内摩擦角的增大，土拱效应越明显，桩后应力偏转现象越明显，但是，土体内摩擦角的改变对土拱形状的影响不明显，在本算例中由于黏聚力较大(c=30 kPa)，桩的荷载分担比改变不大。

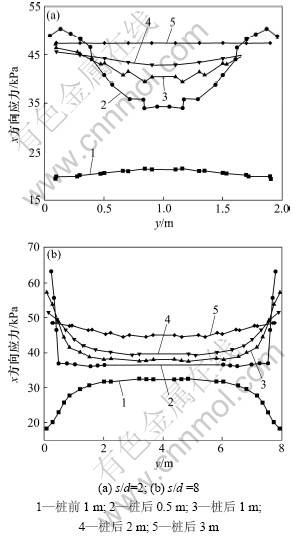
图4  不同桩间距条件下桩间土体关键y剖面上应力分量σ_x的分布曲线

Fig.4  Variation of stress component (σ_x) along critical y-section line under different pile spaces

图5  不同桩间距下两桩中轴线上应力分量σ_y的分布曲线

Fig.5  Variation of stress component (σ_y) along central line between two piles under different pile spaces

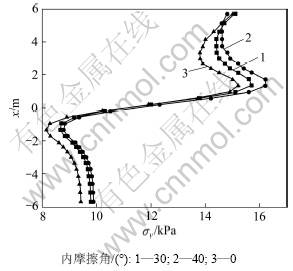
图6  不同内摩擦角下两桩中轴线上应力σ_y的分布曲线

Fig.6  Variation of stress component (σ_y) along central line between two piles under different internal friction angles

3.2  黏聚力的影响

在基本算例中其他参数不变的情况下，分别对土体在黏聚力c=0，20，40，70，100 kPa等情况下进行计算分析。图7给出了4种不同黏聚力下两桩中轴线上应力σ_y分布曲线。经计算发现，随着土体黏聚力的增大，土拱形状由三角形发展成椭圆形和拱形，黏聚力在70 kPa以上土拱形状变化不大；随着土体黏聚力的增大，土拱效应越明显，桩后土拱范围扩大，桩后应力偏转现象越明显，桩的荷载分担比增大。

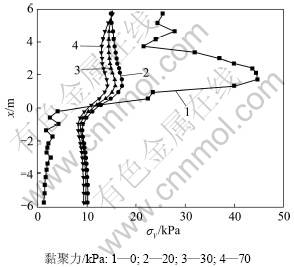
图7  不同土体黏聚力下两桩中轴线上应力分量σ_y分布曲线

Fig.7  Variation of stress component (σ_y) along central line between two piles under different cohesions

3.3  弹性模量的影响

在基本算例中其他参数不变的情况下，分别对土体在弹性模量E =10，50，100 MPa等情况下进行计算分析，图8所示为不同弹性模量下两桩中轴线上的应力分量σ_y曲线图。可见：当土体的弹性模量较小时，桩间土体沿滑动方向的位移较大，随着土体的弹性模量的增大，土体滑动位移变小，土体塑性区域逐渐变小，土拱效应减弱，桩的荷载分担比减小。这说明土拱效应的形成与桩土体之间的相对弹性模量有关，桩土相对弹性模量越大，桩土相对位移越大，土拱效应越明显。

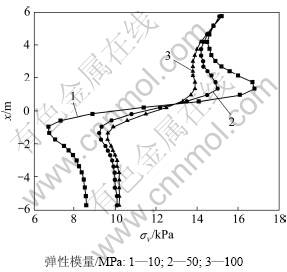
图8  不同弹性模量下两桩中轴线上的应力分量σ_y曲线

Fig.8  Variation of stress component (σ_y) along central line between two piles under different elastic modulus

3.4  泊松比的影响

在基本算例的其他参数不变的情况下，分别对土体在泊松比ν=0.20，0.30，0.45等情况下进行计算分析，图9所示为不同泊松比下两桩中轴线上应力σ_y分布曲线。可见：随着土体的泊松比的增大，土体的侧向压力增大，桩后土拱形状由抛物线变化为近三角形，桩后土拱范围减小；相反，桩间反方向的土拱范围增大，桩的荷载分担比减小，土拱效应减弱。

3.5  膨胀角的影响

在基本算例中其他参数不变的情况下，分别在膨胀角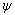为0°和20°等情况下对土体进行计算分析。计算结果表明：随着土体的膨胀角的增大，桩后土拱形状和土拱范围基本不变，桩的荷载分担比也基本上不变化，说明土体的膨胀角对抗滑桩间的土拱效应基本无影响。

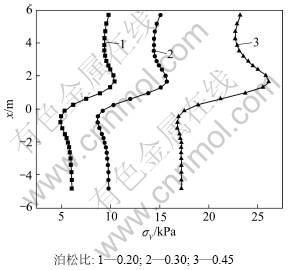
图9  不同泊松比下两桩中轴线上的σ_y曲线

Fig.9  Variation of stress component (σ_y) along central line between two piles under different Poisson’s ratios

4  接触面性状对土拱效应的影响分析

在FLAC^3D软件中，通过改变接触面单元的内摩擦角和黏聚力，来模拟桩土之间的不同接触面性状。令接触面的内摩擦角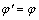(土的内摩擦角)和黏聚力c′=c (土的黏聚力)，模拟桩土完全粗糙接触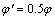；和c′=0.5c模拟桩土之间半粗糙接触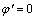；和c′=0模拟桩土之间光滑接触，从而分析接触面性状对土拱效应的影响。图10所示为3种不同接触面性状下两桩中轴线上y方向应力σ_y变化曲线。

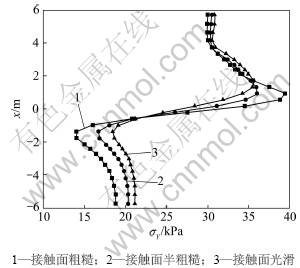
图10  不同桩土接触面下两桩中轴线上的σ_y变化曲线

Fig.10  Variation of stress component (σ_y) along central line between piles under different properties of interface

从计算结果来看，接触面性状对土拱效应的产生也有影响。随着桩土接触面的粗糙程度增加，桩后土拱的范围增大，土拱效应越明显。当桩土之间为光滑接触面时，没有桩间土拱，当桩土粗糙接触时，桩间有明显的反方向土拱，说明此时桩土之间的黏结和摩擦对土体产生了拖曳作用。桩土之间越光滑，土体沿滑动方向的位移越大，桩身附近的土体越容易产生绕流。通过计算发现，随着桩土接触面的粗糙程度增加，桩的荷载分担比也增大。

5  结论

(1) 抗滑桩在桩后水平推力的作用下，由于抗滑桩对土体的约束，在抗滑桩后的土体中形成了明显的应力拱，同时，在桩间至桩前土体中也会出现微弱反方向的应力拱。

(2) 抗滑桩的桩间距对土拱效应的影响很大，随着桩间距的增大，土拱范围变小，土拱形状也由拱形发展到扁平抛物线形，桩的荷载分担比降低，极限桩间距约为s=8d。

(3) 土体性质的改变对抗滑桩间的土拱效应影响明显。土体内摩擦角、土体黏聚力以及桩土之间的相对弹性模量对土拱效应的影响呈正比关系，而土体的泊松比对桩后土拱效应的影响呈反比关系，土体的膨胀角对土拱效应影响不太明显。

(4) 桩土接触面性状对土拱效应存在影响，随着桩土接触面的粗糙程度增加，桩后土拱的范围增大，土拱效应也越显著。

(5) 在工程中为了有效利用桩间土体的土拱效应，应控制合理的桩间距，提高土体的内摩擦角和黏聚力，增加桩土体之间的相对弹性模量，增加桩土接触面的粗糙程度(如设摩擦桩)，从而提高桩土荷载分担比，实现抗滑桩对土体的加固。

参考文献：

[1] Terzaghi K. Theoretical soil mechanics[M]. New York: John Wiley & Son, 1943: 66-76.

[2] Ladanyi B, Hoyaux B. A study of the trap door problem in agranular mass[J]. Canadian Geotechnical Journal, 1969, 6(1): 1-140.

[3] Vardoulakis I, Graf B, Gudehus G. Trap-door problem with dry sand: A statically approach based upon model kinematics[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1981, 5(1): 57-58.

[4] Koutsabeloulis N C, Griffiths D V. Numerical modeling of the trap door problem[J]. Geotechnique, 1989，39(1): 77-89.

[5] Wang D L, Yen B C. Soil arching in slopes[J]. Journal of Geoteechnical Engineering division, ASCE, 1974, 104(GT4): 493-496.

[6] Richard L H. The arch in soil arching[J]. Journal of Geotechnical Engineering, 1985, 111(3): 302-318.

[7] Bosscher J, Cray H. Soil arching in sandy slopes [J]. Journal of Geoteechnical Engineering, 1986, 112(6): 626-645.

[8] Kellogg C G. Discussion of “the arch in soil arching”[J]. Journal of Geoteechnical Engineering, 1987, 113(3): 269-271.

[9] Park K H, Salgado R. Estimation of active earth pressure against rigid retaining walls considering arching effect[J]. Geotechnique, 2003, 53(7): 643-653.

[10] 夏元友, 芮瑞. 刚性桩加固软土路基竖向土拱效应的试验分析[J]. 岩土工程学报, 2006(3): 327-331.
XIA Yuan-you, RUI Rui. Experimental analysis of vertical soil arching effect of embankment reinforced by rigid piles[J]. Chinese Journal of Geotechnical Engineering, 2006(3): 327-331.

[11] 杨明, 姚令侃, 王广军. 抗滑桩宽度与桩间距对桩间土拱效应的影响研究[J]. 岩土工程学报, 2007, 29(10): 1477-1482.
YANG Ming, YAO Ling-kan, WANG Guang-jun. Study on effect of width and space of anti-slide piles on soil arching between piles[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(10): 1477-1482.

[12] 杨明, 姚令侃, 王广军. 桩间土拱效应离心模型试验及数值模拟研究[J]. 岩土力学, 2008, 29(3): 817-822.
YANG Ming, YAO Ling-kan, WANG Guang-jun. Study of centrifuge model tests and numerical simulation on soil arching in space of piles[J]. Rock and Soil Mechanics, 2008, 29(3): 817-822.

[13] 彭述权, 周健, 樊玲, 等. 考虑土拱效应刚性挡墙土压力研究[J]. 岩土力学, 2008, 29(10): 2701-2707.
PENG Shu-quan, ZHOU Jian, FAN Ling, et al. Research on earth pressure of rigid retaining wall considering soil arching[J]. Rock and Soil Mechanics, 2008, 29(10): 2701-2707.

[14] 戴自航, 彭振斌. 土体滑坡治理的合理设计与计算[J]. 中南工业大学学报: 自然科学版, 2000, 31(2): 7-10.
DAI Zi-hang, PENG Zhen-bin. The reasonable design and calculation of curing earth slides[J]. Journal Central South University of Technology: Natural Science, 2000, 31(2): 7-10.

[15] 贾致荣, 谭炜. 桩承路堤土拱效应现场试验与分析[J]. 工程勘察, 2008, 36(6): 9-12.
JIA Zhi-rong, TAN Wei. Site experiment and analysis of soil arching effect by pile-supported embankment[J]. Geotechnical Investigation & Surveying, 2008, 36(6): 9-12.

[16] 李忠诚, 洪昌地. 侧移土体被动桩成拱效应分析[J]. 岩土力学, 2008, 29(6): 1711-1715.
LI Zhong-cheng, HONG Chang-di. Soil arching action in passive piles under lateral displaced soil[J]. Rock and Soil Mechanics, 2008, 29(6): 1711-1715.

(编辑 赵俊)

收稿日期：2010-10-29；修回日期：2011-01-05

基金项目：国家自然科学基金和上海宝钢集团公司联合资助项目(51074177)

通信作者：李地元(1981-)，男，湖南新邵人，博士，讲师，从事岩土力学和岩土工程研究；电话：13517407018；E-mail: ldy-324@163.com