城市轨道交通列车-浮置板式轨道系统竖向振动模型

向  俊，王  阳，赫  丹，孔凡兵，郭高杰

(中南大学 土木建筑学院，湖南 长沙，410075)

摘  要：针对浮置板式轨道结构特点，取相邻2个扣件之间的轨道为1个轨段单元，钢轨视为连续弹性点支承Euler梁，浮置板视为弹性薄板，扣件系统及橡胶支座均模拟为线性弹簧及粘滞阻尼器，建立浮置板式轨道振动模型；将城轨列车中的车辆均离散为多刚体系统，各刚体之间通过线性弹簧及粘滞阻尼器相连，建立列车振动模型；将浮置板式轨道及列车振动势能叠加，得到系统竖向振动总势能；基于弹性系统动力学总势能不变值原理及形成系统矩阵的“对号入座”法则，建立此系统竖向振动矩阵方程；采用Wilson-θ逐步积分法求解此矩阵方程，得出此系统竖向振动响应。研究结果表明：采用浮置板式轨道振动模型计算的钢轨竖向位移为4.18 mm, 浮置板竖向位移为0.69 mm，与已有研究结果吻合良好；城轨列车以速度60 km/h在浮置板式轨道上运行时的系统竖向振动响应波形图符合物理概念，响应的量值反映了系统竖向振动的通常幅值。

关键词：浮置板轨道；地铁车辆；竖向振动

中图分类号：U239.3；U213.2         文献标识码：A         文章编号：1672-7207(2008)03-0596-06

Model of vertical vibration of train and floating slab track system in

 urban rail transit system

XIANG Jun, WANG Yang, HE Dan, KONG Fan-bing, GUO Gao-jie

(School of Civil and Architectural Engineering, Central South University, Changsha 410075, China)

Abstract: According to structural characteristics of floating slab tracks, a track segment element was taken between two adjacent fasteners. For each element, rails were regarded as Euler beams supported by discrete viscoelastic supports. The fasteners and rubber supports were replaced by a linear spring and damp. So the vibration model of the floating slab track was established. In constructing vibration model of a metro train, each car of the metro train with two suspensions was modeled as a multi-rigid body system, in which rigid bodies were connected with each other by a linear spring and damp. Combining the potential energy of vertical vibration of the track with that of the metro train, the total potential energy of vertical vibration of the train and track was obtained. And then, the matrix equation of vertical vibration of the system was established using the principle of total potential energy with stationary value in elastic system dynamics and the “set-in-right-position” rule for formulating system matrices. The vibration responses of the system can be obtained by solving the matrix equation with the direct time integration such as Wilson-θ method. The results show that by using the floating slab track vibration model, the vertical rail displacement is 4.18 mm and the vertical floating slab displacement is 0.69 mm, which is consistent with the existing results. When the metro train runs on the floating slab track at 60 km/h, the waveforms of vertical vibration of the system accord with the physic concepts and the vibration response values reflect the general vibration magnitudes of the system.

Key words: floating slab track; metro vehicle; vertical vibration

城市轨道交通在我国各大城市发展迅速，其周边一般均为居民聚集区，建筑物密集。当今，随着经济的发展，人们的环保意识在逐渐加强，对生活环境水平的要求也不断提高，并且提出了经济与环境可持续发展这一理念。因此，城市轨道交通在迅猛发展的同时引起的振动和噪声问题自然备受关注。世界许多国家都开展了对轨道交通引起的振动噪声问题的研   究^[1]。近年来，许多国家在城市轨道交通中采用一种降噪效果较明显的轨道结构-浮置板式轨道^[2]。这种轨道结构是用扣件把钢轨固定在钢筋混凝土浮置板上，浮置板置于可调的橡胶支座上，浮置板两侧用弹性材料固定，形成一种质量-弹簧系统^[3]。当城轨列车在浮置板上行驶时，列车与轨道是一个相互影响和相互作用的过程。因此，要进一步了解浮置板轨道结构的动力学性能及其减振机理，应该从列车-轨道系统动力学的角度进行深入研究。王澜等^[4]基于大型商业软件MSC/DYTRAN建立了浮置板式轨道结构与列车耦合系统有限元模型，对比分析了浮置板式轨道结构和普通碎石道床结构系统振动响应，并对浮置板式轨道结构的隔振效果进行了评价；姚京川等^[2]采用ANSYS有限元计算软件分别建立了浮置板式轨道与普通整体道床平面有限元模型，计算了地铁车辆作用下的系统振动响应，并重点讨论了浮置板式轨道结构的减振效果。侯德军等^[5]建立了浮置板轨道结构的双层连续弹性梁模型，用傅里叶变换法并借助MATLAB软件编制程序，求得了浮置板轨道在移动简谐荷载作用下的振动响应。蔡成标等^[6]基于车辆-轨道耦合动力学原理，分别建立了地铁车辆与轨道的动力分析模型，并根据弹性薄板的振动理论，采用双向函数组合级数逼近法求解浮置板振动方程，在此基础上，分析了浮置板轨道过渡段的动力性能。在此，本文作者建立城轨列车与浮置板式轨道系统竖向振动模型，采用FORTRAN语言编制相应计算程序，并对此模型及程序进行验证，以期能进一步分析此系统的振动提供一种方法。

1  城轨列车振动模型

以地铁车辆为例(采用全动车编组，5辆车)，进行列车-浮置板轨道竖向振动分析。将动车离散为具有二系悬挂的多刚体系统，车体及每1个转向架均考虑浮沉、点头2个自由度，每个轮对仅考虑浮沉1个自由度。基于此位移模式，即可导出每一动车的竖向振动势能，其中，下标j表示列车中的动车编号。将所有动车的竖向振动势能相加，便得出城轨列车竖向振动总势能^[7-8]。

2  浮置板式轨道振动模型

2.1  浮置板式轨道基本构造

浮置板式轨道, 顾名思义就是通过弹性体把轨道结构上部建筑与基础完全隔离, 使其处于悬浮状态, 建立质量-弹簧的单自由度系统, 利用整个道床在弹性体上进行惯性运动来隔离和衰减列车运行产生的振动，如图1所示。这种轨道结构是用扣件把钢轨固定在钢筋混凝土浮置板上，浮置板置于可调的橡胶支座上，浮置板两侧用弹性材料固定，形成一种质量-弹簧系统^[3]。

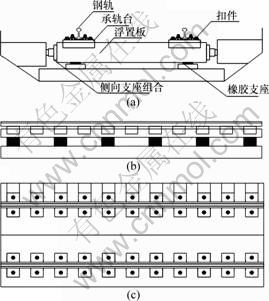
(a) 端视图；(b) 侧视图；(c) 俯视图

图1  浮置板式轨道结构示意图

Fig.1  Diagrams of floating slab track structure

2.2  浮置板式轨道振动模型

针对浮置板式轨道结构特点，取相邻2个扣件之间的轨道为1个轨段单元，在每1个单元中，将钢轨视为连续弹性点支承Euler梁，浮置板视为弹性薄板，扣件系统及浮置板下面的橡胶支座均模拟为点支承的线性弹簧及粘滞阻尼器，不考虑橡胶支座下面的混凝土底座的振动，从而建立浮置板式轨道结构的竖向振动模型，如图2所示。取如下变位参数来描述图2中的轨段单元节点位移：

图2  浮置板式轨道的轨段单元模型

Fig.2  Model of track segment element of floating slab tracks

在确定了单元节点位移参数后，就可以按照一定的插值方法得到单元内部任意点处的位移表示式。下面研究单元中浮置板上任意1点的竖向位移的插值方法。如图2所示，在浮置板段中沿Y轴方向任取一单位宽的横向有限条abcd，并可视为梁段ij，则梁段ij上任意1点的挠度W可用其两端点i和j的变位参数并采用Hermitian 3次方插值函数插值得到；而i和j两端点处的变位参数又可用板段单元的角点位移插值得到，其中线位移采用Hermitian 3次方插值函数插值，转角采用线性插值。最后，可得浮置板上任一点处的竖向位移表示式。上述有关浮置板竖向位移插值的方法，称为“横向有限条与板段单元”分析方法。这种方法与一般的板单元相比，具有简单、实用的特点^[9-13]。

利用上述位移模式就可以导出轨段单元中钢轨和浮置板的弹性变形能及惯性力势能，扣件及浮置板下面的橡胶支座的弹性变形能和阻尼力势能。将这些势能相加，即可得到第个轨段单元的竖向振动势能。则对于划分了N_z个轨段单元的浮置板式轨道的竖向振动总势能为

3  系统振动矩阵方程的建立及其求解

设在t时刻浮置板式轨道的计算长度上有M辆车，则此时浮置板式轨道上城轨列车的空间振动总势能可以写为

将式(4)与式(5)相加，即可得出城轨列车-浮置板式轨道时变系统在t时刻的竖向振动总势能为

根据弹性系统动力学总势能不变值原理^[14]及形成系统矩阵的“对号入座”法则^[15]，此系统在t时刻的竖向振动矩阵方程为

式(7)考虑了轮轨衔接条件，包括轮轨位移衔接条件(车轮竖向位移=钢轨竖向位移+轨道竖向几何不平顺+轮轨竖向相对位移)和轮轨相互作用力的衔接条件(轮轨之间的相互作用力是1对作用力与反作用力，用静轮重力加上列车竖向惯性力来表达)，以此来构建轮轨间的垂向作用模型。根据美国六级轨道谱产生的轨道竖向随机不平顺作为系统竖向振动的激振源，采用Wilson-θ数值积分法对式(7)进行求解。在此基础上，利用FORTRAN语言编制计算程序TFSTSVA(Train and floating slab track system vibration analysis)。

4  模型验证

为了便于分析和比较，采用文献[16]中的车辆及浮置板式轨道动力学参数，基于本文模型及程序TFSTSVA，计算了单节地铁车辆以60 km/h速度在浮置板式轨道上运行时的系统竖向振动响应，其中，浮置板式轨道计算长度取为125 m。表1所示为钢轨与浮置板的最大竖向位移。文献[16]中采用车辆-浮置板轨道垂向耦合动力分析模型，运用Matlab语言进行编程计算，所得出的钢轨与浮置板的最大竖向位移见表1。由表1可见，采用自编程序所得计算结果与文献[16]中计算结果基本吻合，初步验证了本文模型及程序的正确性。

表1  本文计算结果与文献[16]中结果的比较

Table 1  Comparison of calculated results obtained by model of this paper with those in Ref.[16]

对城轨列车以速度60 km/h在计算长度为125 m的浮置板式轨道上运行时的系统竖向振动响应进行计算。其中，城轨列车以地铁车辆为例，采用5辆全动车编组。有关车辆及浮置板式轨道动力学参数见文献[16]。整个系统竖向动力学指标包括系统各个部件的竖向位移、速度、加速度，轮轨相互作用力，轮重减载率，列车乘坐舒适度，钢轨对于浮置板的竖向压力等。这里只列出了部分具有代表性的系统竖向振动响应时程曲线，具体为：钢轨竖向位移(图3)，钢轨竖向加速度(图4)，浮置板竖向位移(图5)，浮置板竖向加速度(图6)，车体竖向加速度(图7)与轮轨竖向作用力(图8)。

图3  钢轨竖向位移时程曲线

Fig.3  Time history curve of vertical rail displacement

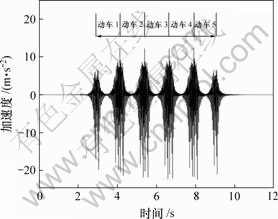
图4  钢轨竖向加速度时程曲线

Fig.4  Time history curve of vertical rail acceleration

图5  浮置板竖向位移时程曲线

Fig.5  Time history curve of vertical floating slab displacement

图6  浮置板竖向加速度时程曲线

Fig.6  Time history curve of vertical floating slab acceleration

图7  第3辆车的车体竖向加速度时程曲线

Fig.7  Time history curve of vertical car body acceleration of the third metro vehicle

图8  第3辆车轮轨竖向作用力时程曲线

Fig.8  Time history curve of vertical wheel-rail force of the third metro vehicle

由图3及图4可见，当车轮经过浮置板式轨道某断面或观测点(取轨道计算中点)时，钢轨竖向位移及加速度达到最大值；车轮距离观测点位置越近，其值越大；车轮距离观测点位置越远，其值越小；从图3和图4还可清晰地看出列车中的车辆数目。这在图5和图6中也存在这种规律。另外，由图3~8可见，钢轨和浮置板的竖向位移及加速度、车体竖向加速度与轮轨竖向作用力等均在通常振动值范围内，反映了城轨列车—浮置板式轨道系统竖向振动的一般状态。因此，从此系统竖向振动响应的波形图及其量值来看，说明所编程序是正确的。

5  结  论

a. 根据浮置板式轨道结构特点，建立了浮置板式轨道的轨段单元模型，采用所提出的横向有限条与板段单元法对浮置板竖向位移进行插值。计算结果表明，该模型及程序正确、可靠。

b. 采用本文模型可以同时计算城轨列车及浮置板式轨道结构的振动响应，便于进行系统参数的敏感性分析。

c. 本文模型及程序可用于分析城轨列车-浮置板式轨道系统振动及指导浮置板式轨道结构的设计和养护维修工作。

参考文献：

[1] 姚京川, 杨宜谦, 孙 宁. 浮置板式轨道结构的发展[J]. 中国铁路, 2003(7): 20-22.

YAO Jing-chuan, YANG Yi-qian, SUN Ning. Development of floated slab track structure[J]. Chinese Railways, 2003(7): 20-22.

[2] 姚京川, 杨宜谦, 王 澜. 浮置板式轨道结构隔振效果分析[J]. 振动与冲击, 2005, 24(6): 108-110.

YAO Jing-chuan, YANG Yi-qian, WANG Lan. Vibration isolation effect analysis of floating slab track[J]. Journal of Vibration and Shock, 2005, 24(6): 108-110.

[3] 严 华, 姚 力. 浮置板轨道设计[J]. 铁道工程学报, 2002(4): 12-15.

YAN Hua, YAO Li. Design of track laying with floating plate[J]. Journal of Railway Engineering Society, 2002(4): 12-15.

[4] 王 澜, 宣 言, 万 家, 等. 浮置板式轨道结构隔振效果仿真研究[J]. 中国铁道科学, 2005, 26(6): 48-52.
WANG Lan, XUAN Yan, WAN Jia, et al. The simulation research on the vibration insulation performance of the floating slab track structure[J]. China Railway Science, 2005, 26(6): 48-52.

[5] 侯德军, 雷晓燕, 刘庆杰. 浮置板轨道系统动力响应分析[J]. 铁道工程学报, 2006(8): 18-24.

HOU De-jun, LEI Xiao-yan, LIU Qing-jie. Analysis of dynamical responses of floating slab track system[J]. Journal of Railway Engineering Society, 2006(8): 18-24.

[6] 蔡成标, 刘增杰, 赵汝康. 浮置板轨道过渡段的动力学设计[J]. 铁道建筑, 2003(12): 41-44.
CAI Cheng-biao, LIU Zeng-jie, ZHAO Ru-kang. Dynamical design of floating slab in track transition section[J]. Railway Engineering, 2003(12): 41-44.

[7] XIANG Jun, LI De-jian, ZENG Qing-yuan. Simulation of spatially coupling dynamic response of train-track time-variant system[J]. Journal of Central South University of Technology, 2003, 10(3): 226-230.

[8] 曾庆元, 向 俊, 周智辉, 等. 列车脱轨分析理论与应用[M]. 长沙: 中南大学出版社, 2006.

ZENG Qing-yuan, XIANG Jun, ZHOU Zhi-hui. Analysis theory and application of train derailment[M]. Changsha: Central South University Press, 2006.

[9] XIANG Jun, HE Dan, ZENG Qing-yuan. Analysis theory of spatial vibration of high-speed train and slab track system[J]. Journal of Central South University of Technology, 2008, 15(1): 121-126.

[10] 向 俊, 赫 丹, 曾庆元. 横向有限条与无碴轨道板段单元的车轨系统竖向振动分析法[J]. 铁道学报, 2007, 29(4): 64-69.

XIANG Jun, HE Dan, ZENG Qing-yuan. Analysis method of vertical vibration of train and ballastless track system with the lateral finite strip and slab segment element[J]. Journal of the China Railway Society, 2007, 29(4): 64-69.

[11] 向 俊, 赫 丹. 高速列车与博格板式轨道系统竖向振动分析模型[J]. 交通运输工程学报, 2007, 7(3): 1-5.

XIANG Jun, HE Dan. Analysis model of vertical vibration of high-speed train and B?gl slab track system[J]. Journal of Traffic and Transportation Engineering, 2007, 7(3): 1-5.

[12] 向 俊, 曹 晔, 刘保钢, 等. 客运专线板式无碴轨道动力设计参数[J]. 中南大学学报: 自然科学版, 2007, 38(5): 981-986.

XIANG Jun, CAO Ye, LIU Bao-gang, et al. Dynamic parameters of slab track of passenger transport line[J]. Journal of Central South University: Science and Technology, 2007, 38(5): 981-986.

[13] 赫 丹, 向 俊, 曾庆元. 一种无碴轨道动力学建模的新方法[J]. 中南大学学报: 自然科学版, 2007, 38(6): 1206-1211.

HE Dan, XIANG Jun, ZENG Qing-yuan. A new method for dynamics modeling of ballastless track[J]. Journal of Central South University: Science and Technology, 2007, 38(6): 1206-1211.

[14] ZENG Qing-yuan, LOU Ping, XIANG Jun. The principle of total potential energy with stationary value in elastic system dynamics and its application to the analysis of vibration and dynamic stability[J]. Journal of Huazhong University of Science & Technology: Urban Science Edition, 2002, 19(1): 7-14.

[15] 曾庆元, 杨 平. 形成矩阵的“对号入座”法则与桁梁空间分析的桁段有限元法[J]. 铁道学报, 1986, 8(2): 48-59.
ZENG Qing-yuan, YANG Ping. The “SET-in-right-position” rule for forming structural matrices and the finite truss-element method for space analysis of truss bridge[J]. Journal of the China Railway Society, 1986, 8(2): 48-59.

[16] 张格妍. 车辆-浮置板轨道垂向耦合动力特性研究[D]. 北京: 北京交通大学土木建筑学院, 2004.
ZHANG Ge-yan. Researches on vertical coupling dynamic models of train-floating slab system and its dynamic responses[D]. Beijing: School of Civil Engineering and Architecture, Beijing Jiaotong University, 2004.

收稿日期：2007-12-21；修回日期：2008-02-16

基金项目：国家重点基础研究发展计划资助项目(2007CB714706)；国家自然科学基金资助项目(50678176，50078006)；教育部新世纪优秀人才支持计划资助项目(NCET-07-0866)；铁道部科技研究开发计划资助项目(2006G009-A)

通信作者：向  俊(1968-)，男，湖南沅陵人，博士，教授，从事车轨(桥)系统振动、列车脱轨及轨道动力学研究；电话：0731-2656645；E-mail: jxiang@mail.csu.edu.cn