文章编号:1004-0609(2013)06-1681-13
复杂介质条件下CSAMT最小发收距的选择
汤井田1, 2,周 聪1, 2,肖 晓1, 2
(1. 中南大学 有色金属成矿预测教育部重点实验室,长沙 410083;
2. 中南大学 地球科学与信息物理学院,长沙 410083)
摘 要:提出利用CSAMT与MT的响应相对误差来区分CSAMT近区、过渡区与远区场数据的方法,考虑发收距r、测量角度φ、测深频率f、覆盖层厚度h1和各层电阻率等因素。通过3种数值模型,讨论复杂介质条件下最小发收距rmin的选择方案。结果表明:均匀半空间模型中,rmin的值可精确给定;两层介质时,rmin的选择需根据勘探深度分情况讨论;多层介质时,可等效成两层介质进行估计。
关键词:地球物理;电磁勘探;可控源音频大地电磁法;复杂介质;测量范围;发收距
中图分类号:P631.3 文献标志码:A
Selection of minimum transmit-receive distance of CSAMT on complicated media
TANG Jing-tian1, 2, ZHOU Cong1, 2, XIAO Xiao1, 2
(1. Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education, Central South University, Changsha 410083, China;
2. School of Info-physics and Geomatics Engineering, Central South University, Changsha 410083, China)
Abstract: A method used to identify the near-field area, transition-field area and the far-filed area were proposed by the relative error of the responses of the CSAMT and MT. The transmit-receive distance r, angle φ, frequency f, overburden thickness h1 and resistivity of each layer were considered. The approaches used to select the optimal rmin were demonstrated based on three numerical models. The results show that, on homogeneous half-space, rmin can be given precisely. On two layer model, rmin is calculated by different cases with different exploration depth. On multi-layer model, rmin can be estimated by a equivalent two layered model.
Key words: geophysics; electromagnetic prospecting; controlled source audio-frequency magnetotelluric; complicated media; measure zone; transmit-receive distance
近年来,可控源音频大地电磁法(Controlled source audio-frequency magnetotelluric,CSAMT)因其理论方法、数据处理技术和实用仪器的改善,在资源勘查等领域得到了迅速的发展及应用。相比无源的大地电磁法(Magnetotelluric,MT),由于引入了可控的电流源,因而获得了很高的信噪比,并在合适的测量排列下具备很高的工作效率。然而,同样由于源的引入,产生了一系列与源有关的问题[1-6],非平面波效应[2-3]即是其中之一。很多学者对非平面波校正这一问题进行过研究,如UMESH[7]、曹昌祺[8]等分别提出过不同的视电阻率定义,汤井田等[9-10]在全区视电阻率的定义及应用方面作过大量研究。然而就目前的实际应用而言,野外作业时尽量保证在远区场观测依然是最为合理的方案。随着资源勘查日益走向深部,CSAMT的目标勘探深度也常被要求尽可能大。一些学者讨论了CSAMT对深部及多层条件下地电体的分辨情况[11-12],很多应用实例[13-14]也论证了CSAMT对大深度勘探的有效性。但大深度的测量使得非平面波效应的问题更加凸显,实际工作中如设计不当,很难保证所有频率都在远区范围内。
为在保证信噪比的同时获取更多可用数据,合理的观测方案设计是必要的,而测量区域的选择是其中的关键。一般的,依据背景为测区平均大地电阻率的均匀半空间模型来进行测量区域的划定。如ZONGE[15]指出发收距大于波长的一半即3倍趋肤深度时可近似认为进入远区。PFAFFHUBER[16]研究了均匀大地表面上水平磁偶极子的远区电磁场距离与趋肤深度之间的线性关系, 并给出远区场距离估算公式。岳瑞永等[17]讨论了方位各向异性对近、远区划分的影响。王若等[18]分析了几种不同观测系统的电磁场特征,比较了几种适宜复杂地形的观测方案的优缺点。陈明生等[19]利用均匀半空间表面电磁场的闭合表达式,由地层波与地面波之比给出了定量划分场区的方法。林威[20]探讨水平电偶源条件下过渡区电磁场的特征,并提出在实际工作中可利用卡尼亚视电阻率与电场视电阻率的相交点作为过渡区数据的判断标志。通常而言,当测区地质构造相对简单或探测深度要求不大时,依据均匀半空间的结论得出的施工方案设计是合理的,可以保证数据质量、高信噪比以及生产效率。但一方面,即使是在均匀半空间中,目前依据感应数p进行的远区、过渡区及近区的划分也并不精确;另一方面,对于某些地质条件较复杂的测区,如基底电阻率很大时,过小的发收距常常会导致过渡区数据采集过多,使得结果难以处理;而基底电阻率很小时,过大的发收距又会使信号强度减弱,信噪比降低。针对这一问题,本文作者将对均匀水平层状介质表面电偶极子源测量区域的选择进行讨论。
1 测量范围的限制因素与远区及过渡区场数据的判别
CSAMT测量中,有限场源的使用对在平面上允许采集数据的范围提出了一些限制。确定允许勘探范围的因素有3个:1) 最大发收距rmax,它受到给定噪声条件下最小可测信号的制约;2) 最小发收距rmin,它受到进入过渡区与近区带的限制;3) 信号强度与偏离场源中垂线的方位角的依赖联系(对水平电偶源)。
通常,根据所要求的勘探深度以及测量区域的大地电阻率(可据标本、露头、测井等估计)可确定最低的探测频率fL以及合适的频率范围。由fL可得对应的趋肤深度及所需的最小发收距rmin。理想的情况是rmin尽可能地小,同时对使用的所有频率而言仍保持在远区。而根据给定噪声条件下可探测的最小电场及磁场强度,由电磁场值(E, H)与发收距r的关系式[1-2]可以得到最大发收距rmax=F(Emin, Hmin)。另外,通过研究电偶极源的电磁场分布特征,以避开场值微弱的区域为原则可确定适合进行测量的方位角。
为进行合理的施工方案设计,准确地识别远区、过渡区以及近区范围十分必要。一般根据电距离参数进行分区划定,当发收距大于趋肤深度3~5倍时,认为为远区场[15-20]。显然,这样的划分并不严格。对此,利用MT响应与CSAMT响应进行对比以进行各区域的划定。由于MT观测天然电磁场,不受非平面波效应的影响,因此将其作为CSAMT远区与过渡区的判别依据是可行的。定义参数:
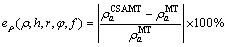 (1)
(1)
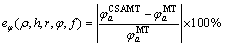 (2)
(2)
式中: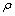 、
、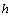 、
、 、
、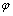 、
、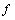 分别为介质电阻率、水平介质层的厚度、发收距、观测角度和观测频率。
分别为介质电阻率、水平介质层的厚度、发收距、观测角度和观测频率。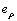 、
、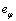 分别为同一地电模型对应于某一类
分别为同一地电模型对应于某一类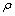 、
、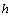 、
、 、
、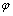 、
、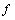 值时CSAMT与MT的响应视电阻率和相位的相对误差;
值时CSAMT与MT的响应视电阻率和相位的相对误差;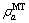 、
、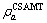 和
和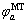 、
、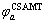 分别为相对应的MT及CSAMT视电阻率及相位响应。
分别为相对应的MT及CSAMT视电阻率及相位响应。
2 水平均匀大地表面测量区域的选择
野外实际工作中,根据勘探目标设计观测区域与频率范围,较完整的CSAMT测量数据常包含远区与部分过渡区的数据。根据水平均匀大地表面各电磁场分量的场值分布[2]及前文提出的相对误差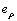 、
、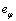 ,可以准确地给出不同误差限下的测量区域范围。
,可以准确地给出不同误差限下的测量区域范围。
图1所示为准静态条件下均匀半空间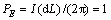 (式中:PE为偶极矩的电偶极矩,I为供电电流,dL为电偶极源的长度)时CSAMT与MT的视电阻率及相位相对误差在大地表面的分布图。图1(a)、(b)、(c)及(d)分别表示
(式中:PE为偶极矩的电偶极矩,I为供电电流,dL为电偶极源的长度)时CSAMT与MT的视电阻率及相位相对误差在大地表面的分布图。图1(a)、(b)、(c)及(d)分别表示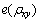 、
、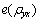 、
、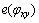 、
、 的分布。
的分布。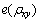 表示xy方向视电阻率的相对误差,其他变量的含义与此类似。PE代表归一化的发射参数,
表示xy方向视电阻率的相对误差,其他变量的含义与此类似。PE代表归一化的发射参数,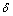 为屈服深度(N代表层数)。其中电偶源的中心位置在(0,0)且垂直y轴放置,
为屈服深度(N代表层数)。其中电偶源的中心位置在(0,0)且垂直y轴放置,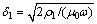 为准静态条件下的趋肤深度,
为准静态条件下的趋肤深度, 为大地的磁导率,x、y分别为与中心位置的距离。
为大地的磁导率,x、y分别为与中心位置的距离。
从图1可以得出以下信息:1) 对于 测量,
测量, 的角域范围内相对误差
的角域范围内相对误差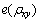 的值较大,不适合进行测量;对于
的值较大,不适合进行测量;对于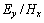 测量,不宜进行测量的角域则为
测量,不宜进行测量的角域则为 。相对误差大的角域与电磁场值微弱的区域[1-2]是一致的,施工设计时应当避开这些角域。2) 在相同的误差限下,与相位相比,依视电阻率的相对误差分布所得的最小发收距rmin的取值要更小,说明相位数据对源的影响更敏感;考虑到实际工作中视电阻率数据更受关注,下文中主要利用视电阻率进行讨论,而如果对相位数据有同样的要求,则rmin的取值必须更大。3) 总体而言,随着发收距
。相对误差大的角域与电磁场值微弱的区域[1-2]是一致的,施工设计时应当避开这些角域。2) 在相同的误差限下,与相位相比,依视电阻率的相对误差分布所得的最小发收距rmin的取值要更小,说明相位数据对源的影响更敏感;考虑到实际工作中视电阻率数据更受关注,下文中主要利用视电阻率进行讨论,而如果对相位数据有同样的要求,则rmin的取值必须更大。3) 总体而言,随着发收距 的减小,误差呈逐渐增大的趋势。表1给出不同视电阻率误差限要求下最小发收距rmin的数值。在野外可根据不同的数据要求来选择rmin。可以看出,汤井田等[1-2]给出的选择结果大约对应于10%的误差限。而如果测量结果中要求误差限更小,则必须将最小发收距的数值取得更大,对于野外常用的赤道
的减小,误差呈逐渐增大的趋势。表1给出不同视电阻率误差限要求下最小发收距rmin的数值。在野外可根据不同的数据要求来选择rmin。可以看出,汤井田等[1-2]给出的选择结果大约对应于10%的误差限。而如果测量结果中要求误差限更小,则必须将最小发收距的数值取得更大,对于野外常用的赤道 测量,只有满足rmin>7δ时,才能保证数据误差限仅为1%。
测量,只有满足rmin>7δ时,才能保证数据误差限仅为1%。
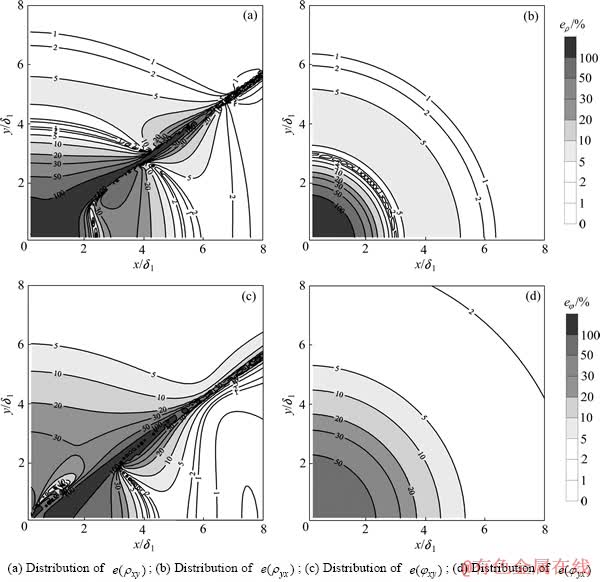
图1 CSAMT与MT的视电阻率、相位相对误差在均匀大地表面的分布图
Fig. 1 Distribution of relative error of CSAMT and MT apparent resistivity on homogeneous halfspace ( ,
,  )
)
表1 均匀半空间时不同视电阻率误差限要求下最小发收距rmin的值
Table 1 Value of rmin by restriction of different apparent resistivity errors on halfspace

3 均匀水平两层介质表面最小发收距的选择
层状介质条件下,模型参数与观测参数之间的关系更复杂,测量区域的选择需要考虑更多因素。为简单起见,先将问题简化为水平两层介质条件。两层时,需要考虑:发收距r,测量角度φ,测深频率f,覆盖层厚度h1,基底与覆盖层的电阻率之比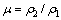 。对于μ值的影响,不妨先取两种理想情况加以研究,即基底良导(
。对于μ值的影响,不妨先取两种理想情况加以研究,即基底良导(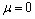 )和基底绝缘(
)和基底绝缘(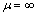 )。可以推测其他μ值条件的影响范围应介于这两者和
)。可以推测其他μ值条件的影响范围应介于这两者和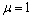 (即均匀半空间)之间。下面先分析两种理想情况下CSAMT的电磁场计算方法及地表视电阻率值的求取方案。
(即均匀半空间)之间。下面先分析两种理想情况下CSAMT的电磁场计算方法及地表视电阻率值的求取方案。
3.1 均匀水平两层理想模型上电偶极子电磁场的计算方法
均匀水平两层介质模型如图2所示。一水平电偶极子(接地导线)位于层状介质表面,偶极矩为P=IdL(I为谐变电流)。选取公共坐标原点O位于偶极子中心的直角坐标系,使x轴指向偶极矩方向(即 φ=0的方向),z轴垂直向下。
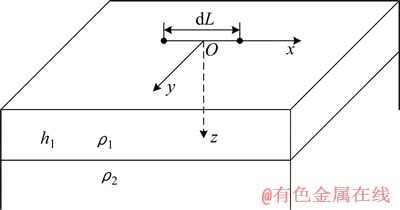
图2 均匀水平两层模型上的水平电偶极子
Fig.2 Electric dipole on two-layer model
当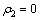 或
或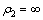 时,即为基地为良导或绝缘的两种理想情况。
时,即为基地为良导或绝缘的两种理想情况。
在电(磁)测深中,各种方法对地电断面的反应完全取决于空间频率特性函数。直流电测深、大地电磁测深和人工源电磁测深的根本异同主要体现在各自的空间频率特性函数上,源只是外在的表现形式。
CSAMT的空间频率特性函数(R*、R)为[1-2]

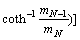 (3)
(3)
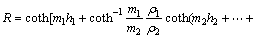
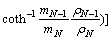 (4)
(4)
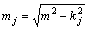 ;
; (5)
(5)
式中:m称为空间频率,它具有距离r倒数的量纲;i为虚数单位;ω为角频率;N为水平多层的层数。
可以发现,CSAMT的空间频率特性函数与观测角度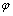 没有关系,或者说地表电磁场随地下介质电阻率或厚度等参数的变化关系不受观测角度
没有关系,或者说地表电磁场随地下介质电阻率或厚度等参数的变化关系不受观测角度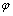 的影响。因此,层状条件下观测角域的选择与均匀半空间类似,这里不再赘述。
的影响。因此,层状条件下观测角域的选择与均匀半空间类似,这里不再赘述。
当层数N=1时,即模型为均匀半空间时,有
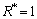 ,
,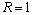 ;
;
当层数N=2时,即模型为两层介质时,可分为两种类型:D型(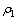 >
>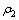 )和G型(
)和G型(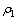 <
<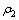 )。将第二层视为均匀半空间,则其顶部处的空间频率特性函数为
)。将第二层视为均匀半空间,则其顶部处的空间频率特性函数为
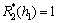 (6)
(6)
 (7)
(7)
由式(3)和(4)可知:
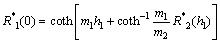 (8)
(8)
 (9)
(9)
变换可得
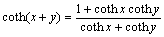
由式(6)和(7)可得:
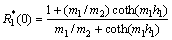 (10)
(10)
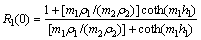 (11)
(11)
1) 当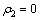 时,由式(5)可知:
时,由式(5)可知:
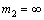 ,
, ,
,
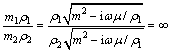 ,
,
将其代入式(10)和(11)中有
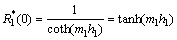 (12)
(12)
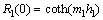 (13)
(13)
2) 当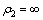 时,由式(5)知
时,由式(5)知
 ,
,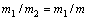 ,
,
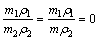 ,
,
将其代入式(10)和(11)中有
 (14)
(14)
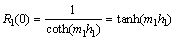 (15)
(15)
以上即是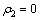 和
和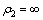 时的空间频率特性函数的计算式,将
时的空间频率特性函数的计算式,将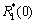 和R 1(0)的值代入水平分层大地表面上谐变偶极子的电磁场各分量计算表达式[1-2]中,即可得这两种理想情况下的电磁场响应,进而可求得这两类条件下的视电阻率值。
和R 1(0)的值代入水平分层大地表面上谐变偶极子的电磁场各分量计算表达式[1-2]中,即可得这两种理想情况下的电磁场响应,进而可求得这两类条件下的视电阻率值。
3.2 均匀水平两层理想模型表面最小发收距的选择
3.2.1 良导基底与绝缘基底的情况
图3所示为两种理想情况下CSAMT与MT的视电阻率相对误差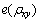 和
和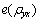 随
随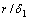 及
及 变化的分布图,
变化的分布图,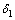 为电磁波在第一层介质中的趋肤深度。图中的虚线表示电阻率为
为电磁波在第一层介质中的趋肤深度。图中的虚线表示电阻率为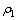 的均匀半空间中
的均匀半空间中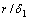 在1%的误差限处的取值。
在1%的误差限处的取值。
设两层介质时选择的最小发收距为rmin(n=2),而依据背景电阻率等于覆盖层电阻率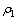 的均匀半空间所选择的最小发收距为
的均匀半空间所选择的最小发收距为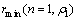 ,其中n表示层数。由图3可看出:1) 层状条件下,各误差限下发收距r与趋肤深度
,其中n表示层数。由图3可看出:1) 层状条件下,各误差限下发收距r与趋肤深度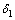 之间的简单线性关系不再成立;只有当
之间的简单线性关系不再成立;只有当 一定时,不同误差限控制的
一定时,不同误差限控制的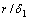 值才不变。2) 若
值才不变。2) 若 << 1,则各误差限处有
<< 1,则各误差限处有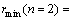
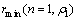 ;如图3(a)中在1%的误差限下,当
;如图3(a)中在1%的误差限下,当 <0.2时,随着
<0.2时,随着 的减小
的减小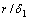 的值不再变化,且与电阻率为
的值不再变化,且与电阻率为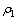 的均匀半空间条件下相同。说明当趋肤深度很小电磁波不足以穿透第一层时,测量相当于在均匀半空间中进行,下层基底的影响可以忽略。3) 若
的均匀半空间条件下相同。说明当趋肤深度很小电磁波不足以穿透第一层时,测量相当于在均匀半空间中进行,下层基底的影响可以忽略。3) 若 >> 1,对良导基底,有
>> 1,对良导基底,有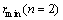 <
<
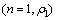 。如图3(a)中在1%的误差限下,当
。如图3(a)中在1%的误差限下,当 >2.8时,随着
>2.8时,随着 的增大,
的增大,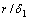 的值逐渐变小,并且其值小于电阻率为
的值逐渐变小,并且其值小于电阻率为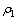 的均匀半空间条件下的取值。对绝缘基底,若
的均匀半空间条件下的取值。对绝缘基底,若 >1,则
>1,则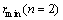 >
>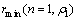 。这说明当趋肤深度很大、电磁波主要在基底中衰减时,各误差限对应的最小发收距主要受基底影响,良导基底对应的最小发收距更小;而绝缘基底对应的最小发收距需更大。4) 若
。这说明当趋肤深度很大、电磁波主要在基底中衰减时,各误差限对应的最小发收距主要受基底影响,良导基底对应的最小发收距更小;而绝缘基底对应的最小发收距需更大。4) 若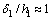 ,对良导基底,大部分区间内有
,对良导基底,大部分区间内有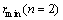 ≥
≥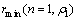 ,仅当
,仅当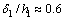 时的一个非常狭窄的区间内在部分误差限下有
时的一个非常狭窄的区间内在部分误差限下有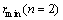 <
<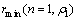 。如图3(a)中1%的误差限下,在0.2<
。如图3(a)中1%的误差限下,在0.2< ≤2.8的范围内,随着
≤2.8的范围内,随着 的增大,
的增大,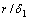 值的整体趋势是先增大后减小,并且其值大于电阻率为
值的整体趋势是先增大后减小,并且其值大于电阻率为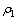 的均匀半空间条件下的取值。对绝缘基底,在
的均匀半空间条件下的取值。对绝缘基底,在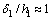 的大部分区间内,
的大部分区间内,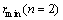 >
>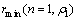 ;仅在0.2<
;仅在0.2< <1间的一个非常狭窄的区间内有
<1间的一个非常狭窄的区间内有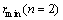 ≤
≤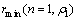 。对于实际工作设计而言,如果目标探测深度要求达到覆盖层以下,则小区间内的特殊情况基本可以忽略。这说明当趋肤深度大致与覆盖层厚度相当时,电磁波的衰减同时受上下两层及分界面的影响,并且这种影响对CSAMT较MT更大。5) 可以发现,在良导基底的理想情况下,在一定的研究范围内(趋肤深度约为覆盖层厚度的2~6倍),对于某一误差限(特别对Ex/Hy测量)
。对于实际工作设计而言,如果目标探测深度要求达到覆盖层以下,则小区间内的特殊情况基本可以忽略。这说明当趋肤深度大致与覆盖层厚度相当时,电磁波的衰减同时受上下两层及分界面的影响,并且这种影响对CSAMT较MT更大。5) 可以发现,在良导基底的理想情况下,在一定的研究范围内(趋肤深度约为覆盖层厚度的2~6倍),对于某一误差限(特别对Ex/Hy测量) 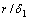 及
及 的变化近似成反比,或者说此时
的变化近似成反比,或者说此时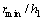 为常数。如对图3(a)所示的10%的误差限,
为常数。如对图3(a)所示的10%的误差限,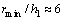 。这说明,对于良导基底,若频率足够低,电磁波透入第二层后会很快衰减,此时的
。这说明,对于良导基底,若频率足够低,电磁波透入第二层后会很快衰减,此时的 的取值仅与覆盖层厚度有关而与测量频率及覆盖层电阻率无关。6) 对于野外常用的赤道Ex/Hy测量,观测角度
的取值仅与覆盖层厚度有关而与测量频率及覆盖层电阻率无关。6) 对于野外常用的赤道Ex/Hy测量,观测角度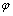 对误差
对误差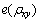 的分布形态影响不大,相对而言,在
的分布形态影响不大,相对而言,在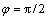 处各误差限对应的rmin值更小;在测线平行偶极矩方向布置时,可以仅考虑
处各误差限对应的rmin值更小;在测线平行偶极矩方向布置时,可以仅考虑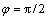 处rmin的取值。轴向Ex/Hy测量及Ey/Hx测量与赤道Ex/Hy测量相比,各误差限下的rmin更小,并且这种差异在良导基底的模型条件下更加明显。说明在高山峡谷等复杂地形条件下,考虑非常规的测量排列可能会使对应误差限下的可测范围更广。
处rmin的取值。轴向Ex/Hy测量及Ey/Hx测量与赤道Ex/Hy测量相比,各误差限下的rmin更小,并且这种差异在良导基底的模型条件下更加明显。说明在高山峡谷等复杂地形条件下,考虑非常规的测量排列可能会使对应误差限下的可测范围更广。

图3 两层介质表面CSAMT与MT的视电阻率相对误差随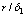 及
及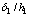 变化的分布
变化的分布
Fig. 3 Distribution of relative error of CSAMT and MT apparent resistivity with constraint of 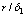 and
and 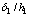 on two-layered earth (dashed line represents value of
on two-layered earth (dashed line represents value of 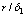 on homogeneous half space with resistivity of ρ1 while restriction error is 1%)
on homogeneous half space with resistivity of ρ1 while restriction error is 1%)
以上所述几种情况详见表2。需要指出的是,以上虽为φ为几个特殊值时所得到的一些结果,但如前所述,由于CSAMT反应层状信息的空间频率特性函数与观测角度φ没有关系,故当φ角在其他角域变化时(应避开场值较弱不适合进行测量的角域)可以得到类似的结果。
表2 两层介质时的最小发收距rmin的值
Table 2 Value of rmin on two-layered earth

3.2.2 非理想条件均匀水平两层介质的情况
前文之所以首先讨论两种理想情况下发收距的选择,是基于非理想条件两层介质的情况应介于均匀半空间与这两种理想情况之间的假设。下面就非理想条件两层介质的情况做一些讨论。同样,设两层介质时选择的最小发收距为rmin(n=2),而依据背景电阻率等于覆盖层电阻率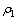 的均匀半空间所选择的最小发收距为
的均匀半空间所选择的最小发收距为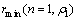 ,依据背景电阻率等于基底电阻率
,依据背景电阻率等于基底电阻率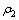 的均匀半空间所选择的最小发收距为rmin(n=1,
的均匀半空间所选择的最小发收距为rmin(n=1,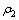 ),其中n表示层数。
),其中n表示层数。
图4所示为 时
时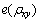 、
、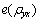 随
随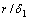 及
及 变化的分布。由图4可以看出:1) 总的来说,非理想条件低阻及高阻基底情况下
变化的分布。由图4可以看出:1) 总的来说,非理想条件低阻及高阻基底情况下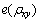 、
、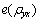 随
随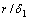 及
及 变化的分布规律与理想条件时基本一致;根据最低探测频率fL或最大趋肤深度
变化的分布规律与理想条件时基本一致;根据最低探测频率fL或最大趋肤深度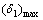 的不同,最小发收距rmin的选择具有3种不同的情况。2) 若
的不同,最小发收距rmin的选择具有3种不同的情况。2) 若 << 1,则各误差限处有
<< 1,则各误差限处有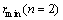 =
=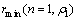 。3) 若
。3) 若 >>1,对低阻基底,有
>>1,对低阻基底,有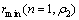 ≤
≤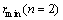 <
<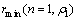 ;对高阻基底,若
;对高阻基底,若 >> 1,则
>> 1,则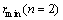 ≥
≥
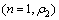 >
>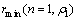 。4) 若
。4) 若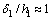 ,对低阻基底,大部分区间内有
,对低阻基底,大部分区间内有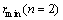 ≥
≥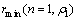 ;对高阻基底,在
;对高阻基底,在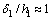 的大部分区间内,
的大部分区间内,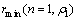 <
<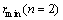 <
<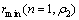 ;仅在0.2<
;仅在0.2< <1间的一个非常狭窄的区间内有
<1间的一个非常狭窄的区间内有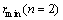 ≤
≤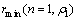 。5) 对低阻基底,
。5) 对低阻基底,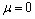 、
、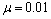 与
与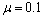 相比较,
相比较, 的各取值区间对应的最小发收距
的各取值区间对应的最小发收距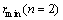 的取值情况介于
的取值情况介于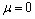 及
及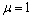 两种情况之间。对高阻基底,
两种情况之间。对高阻基底,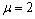 、
、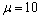 与
与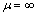 相比较,
相比较, 的各取值区间对应的最小发收距
的各取值区间对应的最小发收距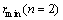 的取值情况介于
的取值情况介于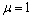 及
及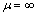 两种情况之间。
两种情况之间。
为进一步证明非理想条件下两层介质的情形介于理想条件和均匀半空间之间,下面讨论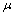 值变化时,
值变化时,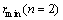 的取值。图5所示为给定h1、
的取值。图5所示为给定h1、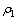 的值在几组不同的发收距r取值下CSAMT与MT的视电阻率相对误差
的值在几组不同的发收距r取值下CSAMT与MT的视电阻率相对误差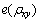 、
、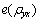 与
与 及
及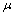 值的变化关系图。由图5可知:1) 非理想条件下,对D型断面,各误差限对应的
值的变化关系图。由图5可知:1) 非理想条件下,对D型断面,各误差限对应的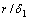 的取值基本处于
的取值基本处于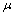 =1及
=1及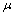 =0两种情况之间。较小的误差限下
=0两种情况之间。较小的误差限下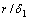 的取值随
的取值随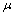 的减小大致递增,在
的减小大致递增,在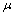 =0处取得最大值;而较大的误差限下
=0处取得最大值;而较大的误差限下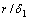 的取值随
的取值随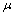 的减小而不断减小,在
的减小而不断减小,在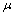 =0处取得最小值。
=0处取得最小值。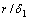 的这种取值趋势随r/h1的增大而由前者向后者过渡。特别的,当r/h1≤1时,
的这种取值趋势随r/h1的增大而由前者向后者过渡。特别的,当r/h1≤1时,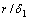 的取值与
的取值与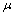 =1即均匀半空间时类似,各误差限下
=1即均匀半空间时类似,各误差限下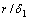 的近似值可参见表1。当
的近似值可参见表1。当 >>1时,
>>1时, 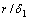 在较大的误差限下随
在较大的误差限下随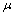 的减小而递减;2) 对G型断面,各误差限对应的
的减小而递减;2) 对G型断面,各误差限对应的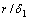 的取值相对简单,一般的,
的取值相对简单,一般的,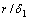 的取值随
的取值随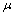 的增大而递增,在
的增大而递增,在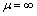 处取得最大值。因此,非理想情况的rmin取值范围基本在两种理想情况与均匀半空间之间。
处取得最大值。因此,非理想情况的rmin取值范围基本在两种理想情况与均匀半空间之间。
实际工作中,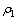 的获取是比较方便的,可以利用标本测量、露头或坑道小四极测量、测井等方法;而h1和
的获取是比较方便的,可以利用标本测量、露头或坑道小四极测量、测井等方法;而h1和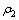 等参数则可通过钻孔等先验资料推测;当h1和
等参数则可通过钻孔等先验资料推测;当h1和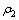 等参数无法预估时,也可根据区域地质情况推知基底类型。一般的,当勘探深度远小于覆盖层厚度(
等参数无法预估时,也可根据区域地质情况推知基底类型。一般的,当勘探深度远小于覆盖层厚度(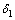 <<h1)时,基底的影响较小,最小发收距rmin的选择与背景电阻率为覆盖层电阻率(
<<h1)时,基底的影响较小,最小发收距rmin的选择与背景电阻率为覆盖层电阻率(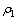 )的均匀半空间情形一致(
)的均匀半空间情形一致(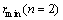 =
=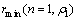 )。当勘探深度与覆盖层厚度相当(
)。当勘探深度与覆盖层厚度相当(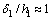 )时,对低阻基底,rmin的取值需大于背景电阻率为
)时,对低阻基底,rmin的取值需大于背景电阻率为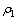 的均匀半空间时的情形(
的均匀半空间时的情形(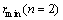 ≥
≥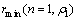 );对高阻基底,rmin的取值则介于背景电阻率分别为
);对高阻基底,rmin的取值则介于背景电阻率分别为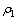 和
和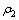 的两种均匀半空间情形之间(
的两种均匀半空间情形之间(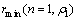 <
<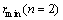 <
<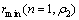 )。当勘探深度远大于覆盖层厚度(
)。当勘探深度远大于覆盖层厚度(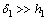 )时,对低阻基底,rmin的取值介于背景电阻率分别为
)时,对低阻基底,rmin的取值介于背景电阻率分别为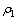 和
和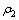 的两种均匀半空间情形之间(
的两种均匀半空间情形之间(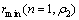 ≤
≤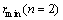 <
<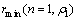 );对于高阻基底,rmin较均匀半空间时必须更大(
);对于高阻基底,rmin较均匀半空间时必须更大(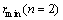 ≥
≥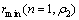 >
>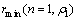 )。rmin的取值情况详见表2。
)。rmin的取值情况详见表2。
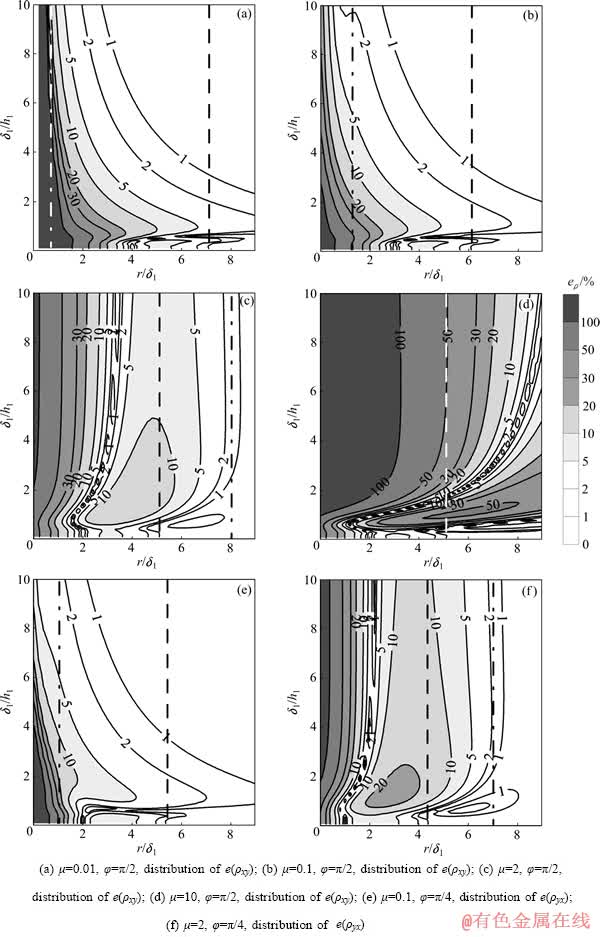
图4 两层介质表面CSAMT与MT的视电阻率相对误差随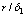 及
及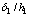 变化的分布
变化的分布
Fig. 4 Distribution of relative error of CSAMT and MT apparent resistivity with constraint of 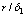 and
and 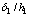 on two-layered earth (dashed line represents value of
on two-layered earth (dashed line represents value of 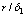 on homogeneous half space with resistivity of ρ1 while restriction error is 1%; dot-dashed line represents value of
on homogeneous half space with resistivity of ρ1 while restriction error is 1%; dot-dashed line represents value of 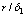 on homogeneous half space with resistivity of ρ2 while restriction error is 1%;
on homogeneous half space with resistivity of ρ2 while restriction error is 1%; 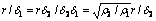 )
)
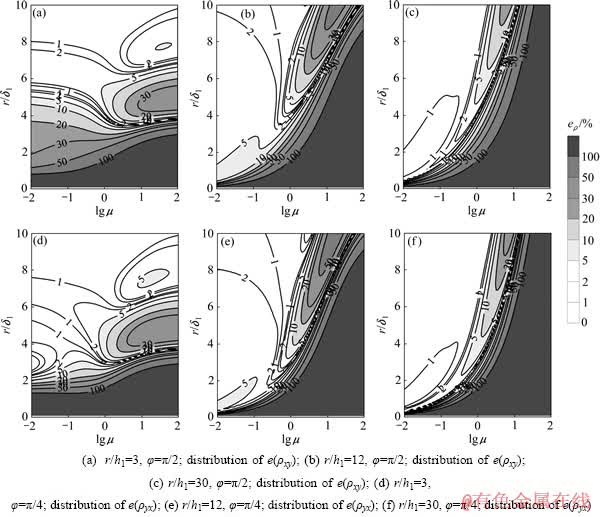
图5 两层介质表面CSAMT与MT的视电阻率相对误差与μ及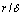 的变化关系
的变化关系
Fig. 5 Distribution of relative error of CSAMT and MT apparent resistivity with constraint of μ and 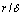 on two-layered earth
on two-layered earth
4 均匀水平多层介质表面发收距的选择
图6所示为均匀水平四层HK及KH模型条件下CSAMT与MT的视电阻率相对误差随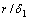 及
及 变化的分布图。由图6可看出,多层条件下的结果与两层条件时基本是类似的,随着频率的降低,也即
变化的分布图。由图6可看出,多层条件下的结果与两层条件时基本是类似的,随着频率的降低,也即 值的增大,各误差限处
值的增大,各误差限处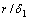 的取值特点依次与D型或G型模型相对应。一般的,rmin的值主要取决于
的取值特点依次与D型或G型模型相对应。一般的,rmin的值主要取决于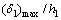 。同样,
。同样, >>1时,低阻层使得误差限对应的可测范围更大,而高阻层则相反,且这种影响随着电阻率差异和层厚的增大而增大。将基底上方各层等效为均匀的一层覆盖层可以将这种影响做一粗略的估计。等效电阻率和厚度计算方法为
>>1时,低阻层使得误差限对应的可测范围更大,而高阻层则相反,且这种影响随着电阻率差异和层厚的增大而增大。将基底上方各层等效为均匀的一层覆盖层可以将这种影响做一粗略的估计。等效电阻率和厚度计算方法为
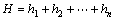 ,
,
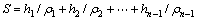 ,
,
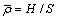
图7所示为CSAMT与MT的视电阻率相对误差在均匀水平四层HK及KH模型及其等效两层模型表面的分布图。由图7可以看出,这种等效的估计方法在5%和10%的误差限下对rmin的判断是可以接受的。

图6 水平四层模型CSAMT与MT的视电阻率相对误差随r/δ1及δ1/h1变化的分布
Fig. 6 Distribution of relative error of CSAMT and MT apparent resistivity with constraint of r/δ1 and δ1/h1 on four-layered models
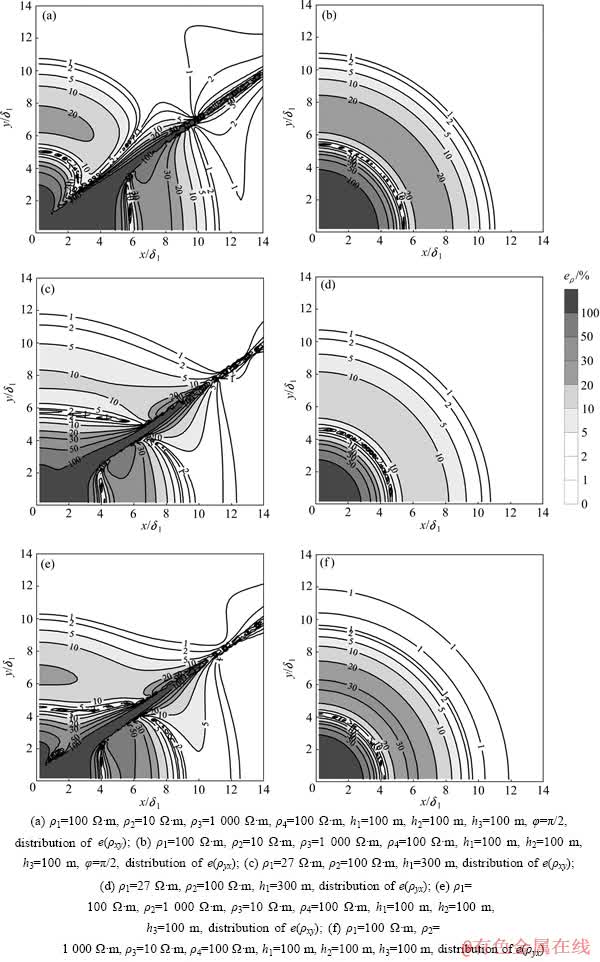
图7 四层及其等效两层模型表面CSAMT与MT的视电阻率相对误差分布
Fig. 7 Distribution of relative error of CSAMT and MT apparent resistivity on surface of four-layered and its equivalent two layered models
综上所述,当目标勘探深度范围内的介质层数较多时,应尽可能多的收集先验信息,并依据这些信息进行综合考量。当各层参数都能粗略估计时,可以利用上述方法判断rmin;当各层参数无法预估而探测深度又要求到达基底时,则主要考虑基底的影响,可以依据背景为基底电阻率的均匀半空间来进行判断。
5 结论
1) 利用CSAMT与MT的响应相对误差来区分CSAMT过渡区与远区场是可行的,并且可以精确的得到各误差限条件下过渡区场的分布范围,进而精确的给出了均匀半空间中不同误差限要求下最小发收距rmin的值以及测量区域的选择范围。对于野外常用的赤道Ex/Hy测量,只有满足rmin>7δ时,才能保证数据误差限仅为1%。
2) 水平两层条件下,因空间频率特性函数不受观测角度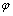 的影响,因此地表测量角域的选择与均匀半空间是一致的。实际工作设计中,对不同的勘探深度,最小发收距rmin的选择具有3种不同的情况,并需获取一定的先验信息,即覆盖层电阻率
的影响,因此地表测量角域的选择与均匀半空间是一致的。实际工作设计中,对不同的勘探深度,最小发收距rmin的选择具有3种不同的情况,并需获取一定的先验信息,即覆盖层电阻率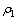 、覆盖层厚度h1和基底电阻率
、覆盖层厚度h1和基底电阻率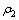 。如能预估h1和
。如能预估h1和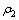 ,则通过CSAMT与MT的视电阻率相对误差随r/δ1及δ1/h1变化的分布即可较准确的得到各误差限下最小发收距rmin值。如h1和
,则通过CSAMT与MT的视电阻率相对误差随r/δ1及δ1/h1变化的分布即可较准确的得到各误差限下最小发收距rmin值。如h1和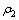 等参数无法预估,可根据区域地质情况推知基底类型。当勘探深度远小于h1时,基底的影响较小, rmin的取值与背景电阻率为
等参数无法预估,可根据区域地质情况推知基底类型。当勘探深度远小于h1时,基底的影响较小, rmin的取值与背景电阻率为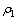 的均匀半空间时的情形一致。当勘探深度与h1相当时,对低阻或高阻基底,rmin的取值均需大于背景电阻率为
的均匀半空间时的情形一致。当勘探深度与h1相当时,对低阻或高阻基底,rmin的取值均需大于背景电阻率为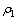 的均匀半空间时的情形。当勘探深度远大于h1时,对低阻基底,rmin的取值较背景电阻率为
的均匀半空间时的情形。当勘探深度远大于h1时,对低阻基底,rmin的取值较背景电阻率为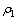 的均匀半空间时的情形可更小;对于高阻基底,rmin的取值较背景电阻率为
的均匀半空间时的情形可更小;对于高阻基底,rmin的取值较背景电阻率为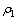 的均匀半空间时的情形更大。
的均匀半空间时的情形更大。
3) 多层条件下的情形与两层条件时基本类似。当勘探深度远大于h1时,低阻层使得误差限对应的可测范围更大,而高阻层则相反,并且这种影响随着电阻率差异和层厚的增大而增大。当目标勘探深度范围内的介质层数较多时,应综合考虑,可利用等效的两层模型对rmin的值进行粗略估计。
REFERENCES
[1] 何继善. 可控源音频大地电磁法[M]. 长沙:中南大学出版社, 1990: 74-130.
HE Ji-shan. Controlled source audio-frequency magnetotellurics[M]. Changsha: Central South University Press, 1990: 74-130.
[2] 汤井田, 何继善. 可控源音频大地电磁法及其应用[M]. 长沙:中南大学出版社,2005: 72-313.
TANG Jing-tian, HE Ji-shan. Methods and applications of controlled source audio-frequency magnetotellurics[M]. Changsha: Central South University Press, 2005: 72-313.
[3] 底青云, 王 若. 可控源音频大地电磁数据正反演及方法应用[M]. 北京: 科学出版社, 2008: 157-165.
DI Qing-yun, WANG Ruo. Methods and applications of controlled source audio-frequency magnetotellurics[M]. Beijing: Science Press, 2008: 157-165.
[4] KAUFMAN A A, KELLER G V. 时间域与频率域电磁测深[M]. 北京: 地质出版社, 1987: 13-293.
KAUFMAN A A, KELLER G V. Time domain and frequency domain electromagnetic sounding[M]. Beijing: Geology Publishing House, 1987: 13-293.
[5] 朴华荣. 电磁测深法原理[M]. 北京: 地质出版社, 1990: 247-259.
PIAO Hua-rong. Theory of electromagnetic sounding method[M]. Beijing: Geology Press, 1990: 247-259.
[6] 高 文. 大地电磁感应的场源效应[J]. 地球物理学报, 1991, 34(2): 210-215.
KAO D Wen. Line source effects on magnetotellurics responses[J]. Chinese Journal Geophysics, 1991, 34(2): 210-215.
[7] UMESH C D. Apparent resistivity curves in controlled-source electromagnetic sounding directly reflecting true resistivities in a layered earth[J]. Geophysics, 1995, 60(1): 53-60.
[8] 曹昌祺. 水平分层大地的交流视电阻率[J]. 地球物理学报, 1978, 21(3): 248-281.
CAO Chang-qi. The apparent resistivity for layered earth[J]. Chinese Journal Geophysics, 1978, 21(3): 248-281.
[9] 汤井田, 何继善. 水平电偶源频率测深中全区视电阻率定义的新方法[J]. 地球物理学报, 1994, 37(4): 543-552.
TANG Jing-tian, HE Ji-shan. A new method to define the full-zone resistivity in horizontal electric dipole frequency soundings on a layered earth[J]. Chinese Journal Geophysics, 1994, 37(4): 543-552.
[10] 汤井田, 周 聪, 张林成. CSAMT电场y方向视电阻率的定义及研究[J]. 吉林大学学报: 地球科学版, 2011, 41(2): 552-558.
TANG Jing-tian, ZHOU Cong, ZHANG Lin-cheng. A new apparent resistivity of CSAMT defined by electric field y-direction[J]. Journal of Jilin University: Earth Science Edition, 2011, 41(2): 552-558.
[11] 汤井田, 周 聪, 邓晓红. CSAMT视电阻率曲线对水平层状大地的识别与分辨[J]. 地质与勘探, 2010, 46(6): 1079-1086.
TANG Jing-tian, ZHOU Cong, DENG Xiao-hong. Identification and discrimination of the horizontal layered earth by using CSAMT apparent resistivity curves[J]. Geology and Exploration, 2010, 46(6): 1079-1086.
[12] 王 艳, 林 君, 周逢道, 张文秀. CSAMT 法深部低阻分辨能力及方法研究[J]. 中国矿业大学学报, 2009, 38(1): 86-90.
WANG Yan, LIN Jun, ZHOU Feng-dao, ZHANG Wen-xiu. Study of resolution and method of CSAMT for the deep low-resistivity[J]. Journal of China University of Mining & Technology, 2009, 38(1): 86-90.
[13] THEODORE H A, DONALD S S. Audiomagnetotelluric characterization of range-front faults, Snake Range, Nevada[J]. Geophysics, 2011, 76(1): B1-B7.
[14] WILT M J, MORRISON H F, LEE K H, GOLDSTEIN N E. Electromagnetic sounding in the Columbia Basin, Yakima, Washington[J]. Geophysics, 1989, 54(8): 952-961.
[15] ZONGE K L. Introduction to CSAMT[M]. Practical Geophysics Ⅱ, Northwest Mining Association, 1992: 1-6.
[16] PFAFFHUBER A. Development and test of a controlled source MT method in the frequency range 1 to 50 kHZ[D]. Berlin: Technical University Berlin, 2001: 10-44.
[17] 岳瑞永, 徐义贤. 可控源频率域电方位各向异性与近场效应研究[J]. 石油地球物理勘探, 2004, 39(3): 342-347.
YUE Rui-yong, XU Yi-xian. Study on electric azimuth anisotropy of controlled source in frequency domain and near-field effects[J]. Oil Geophysical Prospecting, 2004, 39(3): 342-347.
[18] 王 若, 王妙月, 卢元林. 高山峡谷区 CSAMT观测系统研究[J]. 地球物理学进展, 2004, 19(1): 125-130.
WANG Ruo, WANG Miao-yue, LU Yuan-lin. CSAMT observation system study in high mountain and steep gorge area[J]. Progress in Geophysics, 2004, 19(1): 125-130.
[19] 陈明生, 闫 述. CSAMT勘探中场区、记录规则、阴影及场源复印效应的解析研究[J]. 地球物理学报, 2005, 48(4): 951-958.
CHEN Ming-sheng, YAN Shu. Analytical study on field zones, record rules, shadow and source overprint effects in CSAMT exploration[J]. Chinese Journal Geophysics, 2005, 48(4): 951-958.
[20] 林 威. CSAM T法过渡区电磁场的特征[J]. 物探与化探, 2009, 33(2): 148-150.
LIN Wei. Transition region electromagnetic field characteristics of the CSAMT method[J]. Geophysical and Geochemical Exploration, 2009, 33(2): 148-150.
(编辑 李艳红)
基金项目:国家公益性行业基金资助项目(SinoProbe-03);中南大学中央高校基本科研业务费专项资金资助项目(2012zzts011);国家自然科学基金资助项目(41174105)
收稿日期:2012-02-03;修订日期:2013-04-19
通信作者:周 聪,博士研究生;E-mail: jttang@mail.csu.edu.cn