DOI: 10.11817/j.issn.1672-7207.2015.12.041
高压旁路阀流动传热特性
余建平1,俞树荣1,郭晓梅2
(1. 兰州理工大学 石油化工学院,甘肃 兰州,730050;
2. 浙江水利水电学院 机械与汽车工程学院,浙江 杭州,310018)
摘要:为揭示高压旁路阀阀内流体流动传热机理,采用FLUENT软件中的多相流Euler模型数值模拟研究高压旁路阀内部的流动传热过程,然后运用热耦合技术将流场温度耦合到阀体以研究阀体温度分布。研究结果表明:在高压差下,阀内流场速度整体较快,平均流速为10~30 m/s,其中最大流速出现在蒸汽与减温水喷嘴混合处,流速高达80 m/s,阀内温度场总体呈现入口高、出口低的特点,蒸汽入口温度为870 K,出口平均温度为660 K,最低温度出现在拉伐尔喷管处,约为470 K。阀体外表面无保温层时阀体温差大,约为203 K。
关键词:高压旁路阀;数值模拟;传热;两相流
中图分类号:TK39 文献标志码:A 文章编号:1672-7207(2015)12-4693-07
Flow and heat transfer in high-pressure bypass valve
YU Jianping1, YU Shurong1, GUO Xiaomei2
(1. School of Petrochemical Technology, Lanzhou University of Technology, Lanzhou 730050, China;
2. School of Mechanical and Automotive Engineering,
Zhejiang University of Water Resources and Electric Power, Hangzhou 310018, China)
Abstract: Euler multiphase flow model from FLUENT programmer was employed to study the fluid flow and heat transfer mechanisms in high-pressure bypass valve. The temperature distribution of valve body was investigated by coupling flow field temperature to valve body using thermal coupling technology. The results show that the average velocity in the valve is as large as 10-30 m/s under high differential pressure. The maximum velocity with 80 m/s occurs at the position where steam and hot water nozzle are mixed. The temperature in valve shows a gradient distribution with high in inlet and low in outlet, in which the temperature of inlet and outlet are 870 K and 660 K, respectively. The Laval nozzle shows the lowest temperature of 470 K. The temperature difference (about 203 K) of valve body is large when there is no thermal insulation at the outer surface of valve.
Key words: high pressure bypass valve; numerical simulation; heat transfer; two phase flow
旁路系统是汽轮机组热力系统的重要组成部分,起到平衡机组各分系统间的负荷,保护汽轮机和锅炉再热器安全及延长机组寿命的作用[1-3]。高/低压旁路减温减压调节阀作为高/低压旁路系统最重要设备之一,在旁路系统中起减温和减压的作用。由于高/低压弯路阀阀体长期处于高温、高压环境,还要承受很大的温差应力,因而对阀门设计和材料选择是种挑战[4-7]。为此,在动力学方面,鄂加强等[8-10]采用数值仿真分析与实验验证相结合的方法对大口径阀门进行了动力学仿真分析与优化设计研究。Zhu等[11]借助速度控制金属块的方法对天然气管道的可旋转旁通阀的动力学进行研究。Rensburg等[12]对在半主动减振器的延迟时间下的旁路阀的建模进行了仿真分析。Lang等[13]则对旁通阀在失效情况下提取出的HTR-10GT核心的控制棒进行未能紧急停堆的预期瞬态分析。郑海等[14-16]研究了高压旁路阀流场、温度场和应力场以及螺栓。在节能方面,Yang等[17]构建了旁通阀控制策略,并采用旁通阀控制策略来提高气动驱动系统能量效率,取得了较好的效果。在经济方面,杨小琨等[18]应用高压旁路压力调节阀及减温水阀门内漏时汽轮机装置效率变化计算公式,结合300 MW亚临界和600 MW超临界机组的实际数据进行计算,结果表明高压旁路系统阀门内漏对机组热经济性影响较大,且减温水小泄漏的影响程度高于新蒸汽小泄漏的影响程度。综上所述,专家学者们的研究集中在动力学分析、节能以及经济性分析,而较少对高压旁路阀阀内流体流动传热机理进行研究。本文作者采用多相流模型对高压旁路系统中高压旁路阀内部流动传热进行数值模拟,为阀体结构设计提供数据参考。
1 高压旁路阀多相流模型
1.1 高压旁路阀工作原理
高压旁路阀在管路系统中起到调温、调压的作用,其结构较复杂,如图1所示。该旁路阀的工作原理为: 首先套筒式阀芯对水蒸汽进行流量调节,再通过多层孔板结构对蒸汽进行减压,经过减压后的蒸汽再与减温水混合,进一步降温,最终完成减温、减压的作用。
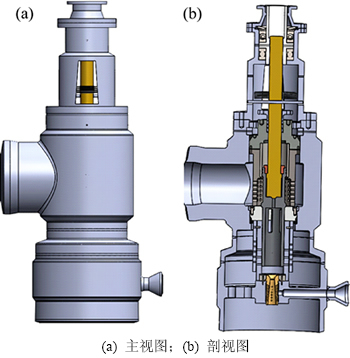
图1 高压旁路阀结构图
Fig. 1 Structure of high pressure bypass valve
1.2 高压旁路阀流动传热数学模型
高压旁路阀的高温过热蒸汽在阀内部与不饱和低温水混合,实现减温、减压的功能,显然属气液两相混合流动。并且由于在设计条件下蒸汽压力由入口的27.0 MPa,降为出口的6.4 MPa,在此过程蒸汽压力变化较大,且远离理想气体状态,应视为可压缩实际气体流动。旁路阀在设计工况下长期运行,各参数不随时间变化,可视为稳态流动。阀内流动的是高温水蒸汽,水蒸汽属三原子非极性分子,正常条件下应考虑水蒸汽与管壁之间的辐射换热,但考虑到阀体会采取保温措施,管壁与水蒸汽温度相差不大,忽略水蒸汽辐射换热。因此,旁路阀流动模型应该为湍流传热汽化相变可压缩两相流动模型。
多流体模型对各相连续介质的数学描述及处理方法均采用欧拉法,因此属于Euler模型。在Euler模型中,不同相看成互相穿插的连续统一体,一相的体积不能被其他相占据,因此,引入相体积分数(phase volume fraction)的概念。相体积分数是空间和时间的连续函数,且在同一空间位置及同一时间各相体积分数之和为1。对每项可导出一组守恒方程,方程组应用本构关系或统计运动学理论封闭。建立欧拉坐标系,可得到关于气液两相流动传热的数学方程。由于多相流动以湍流方式流动,采用RNG k-ε方程作为湍流计算方程。
连续性方程:
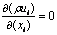 (1)
(1)
动量守恒方程:
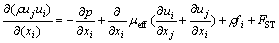 (2)
(2)
湍动能k输运方程:
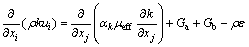 (3)
(3)
湍动能耗散率ε输运方程:
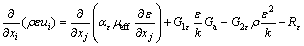 (4)
(4)
其中:ρ为体积平均密度;u为流体速度;x为坐标系位置;下标i或j分别取1,2,3,代表坐标系X,Y,Z的3个方向;p为静压;μeff为有效黏度,其等于分子黏度与湍流黏度之和;fi为质量力;FST为包括表面张力在内的界面力源项;Ga为由于平均速度梯度引起的湍动能产生项;Gb为由于浮力引起的湍动能产生项;G1ε和G2ε为常数,分别为1.42和1.68;αk和αε分别为湍动能与湍动能耗散项的修正系数;湍动能耗散率ε输运方程中的Rε项可表示为
 (5)
(5)
其中:η=Sk/ε;η0=4.38;β=0.012;Cμ为系数,对于RNG模型Cμ=0.084 5;Sk为自定义端动能源相。
蒸汽和液滴的质量随温度变化而变化,以ml→v表示质量由液相转移到气相;mv→l表示质量由气相转移到液相。气液两相之间质量传递主要取决于系统温度,即与该物质液相沸点相关。令Tl为区域内液相温度,Tv为区域内气相温度,Tsat为该液体沸点,则有:
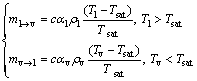 (6)
(6)
式中:αl和αv 分别为气相与液相的容积分数;ρl和 ρv分别为气相与液相的密度;c为转换系数。
在本研究旁路阀工况中,由于阀内压力很高,而水沸点随系统压力变化而变化,所以在数值计算分析过程中,要使用自定义函数功能设置液体沸点随压力而改变,由Antoine公式可知系统压力与沸点关系为
 (7)
(7)
式中:p为计算区域压强,MPa;T为液体沸点,K。
同时,在减温水汽化过程中需要进行能量传递,质量由液相向气相转移过程中将会吸热,即
 (8)
(8)
式中:负号表示吸热;L为蒸发潜热,J/kg;Senergy为能量源项,W/m3。
1.3 仿真设置
图2所示为高压旁路阀三维模型。由于模型结构复杂,计算模型需进行如下简化处理:1) 阀笼部分结构由多层小孔组成,结构复杂,数值计算时采用多孔介质条件,不由软件求解流体通过多层小孔的节流过程,所以,在计算模型中不显示阀笼结构;2) 拉伐尔喷嘴处省略了进水管道结构,直接将喷管壁面设定为入口;3) 为消除流体在进出口中由于扰动而产生的影响,分别在入口和出口设置2D和6D的管路长度。
采用商用软件FLUENT6.3.26进行数值模拟计算。计算模型入口采用质量入口边界条件,质量流量为328 kg/s;出口采用压力出口边界条件,出口压力为6.4 MPa;管路、阀体和内套筒壁面均采用无滑移的壁面边界条件。计算使用基于压力的隐式求解器,使用SIMPLE算法计算耦合压力-速度,方程中压力项使用标准格式离散,其他项使用二阶迎风格式离散,求解器收敛精度设为1.0×10-4。

图2 高压旁路阀三维模型
Fig. 2 Three dimensional model of high pressure bypass valve
2 高压旁路阀流动传热数值模拟
2.1 高压蒸汽旁路阀压力分布
图3所示为高压蒸汽旁路阀截面压力分布云图。
由图3可以看出:入口压力为27 MPa,由于阀笼多层孔板的节流减压作用,流过阀笼后蒸汽压力减小,减压后的出口压力约为8 MPa。
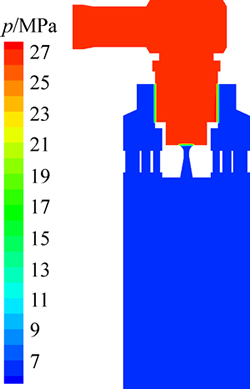
图3 高压蒸汽旁路阀截面压力分布云图
Fig. 3 Pressure distribution on sectional in high-pressure steam bypass valve
2.2 高压蒸汽旁路阀速度分布
图4所示为高压蒸汽旁路阀截面速度分布云图。从图4可以看出:在高压差作用下,阀内部速度整体较快,平均流速为10~30 m/s,其中最大流速出现在蒸汽与减温水喷嘴混合处,此处最大流速接近80 m/s,喷嘴处流速的升高主要是由于拉伐尔渐缩渐扩喷嘴的作用。
根据下式计算当地声速c:
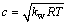 (9)
(9)
式中:水蒸汽绝热指数kw=1.33;水蒸汽气体常数R=461 J/(kg·K)。
计算得当地声速为606 m/s,蒸汽流速还远未达到音速,高压蒸汽旁路阀内流体还是处于亚音速流动状态,这是由于喷嘴内部处于水和水蒸汽的混合阶段,冷却水降低了喷嘴内温度,同时也降低了流速。
此外,阀内速度分布并不是沿管道中轴线方向均匀分布,阀门出口处流体偏向于一侧,这是由于高旁阀结构为角式结构,流体进入阀后须转90°进入多层阀笼,这导致进入阀笼的流体速度出现偏差,进而影响到后半段流体的流动,当然,本图计算工况是阀门全开状态下计算的结果,如果在相对小开度下,这种不对称速度场分布会有所改善。
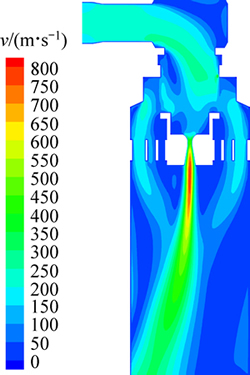
图4 高压蒸汽旁路阀截面速度分布云图
Fig. 4 Velocity distribution on sectional in high-pressure steam bypass valve
2.3 高压蒸汽旁路阀温度分布
图5所示为高压蒸汽旁路阀截面温度分布云图。从图5可看出:阀内温度场总体呈现出入口高、出口低的分布态势,蒸汽入口温度为870 K,出口平均温度为660 K。在阀门出口处及计算区域出口处水蒸汽温度分布并不均匀,这表明适当延长阀后管道长度将有助于得到温度均匀的水蒸汽。计算区域中最低温度出现在拉伐尔喷管处,约为470 K。此外,蒸汽流出阀门时温度分布并不均匀,这是由于水蒸汽与混合水的换热过程要持续一段时间才能达到充分混合换热,温度分布不均匀的另一原因是蒸汽在阀内流动不均匀地偏向一侧,这也导致温度分布改变。
2.4 高压蒸汽旁路阀减温水质量分数分布
图6所示为高压蒸汽旁路阀截面减温水质量分数分布云图。拉伐尔喷嘴是冷却水与高温蒸汽的混合部位,从图6可以看到:减温水进入喷嘴时温度较低约为470 K,但受高温蒸汽的加热作用,在很短时间内减温水温度升至700 K左右,与此同时,减温水也被加热为蒸汽。
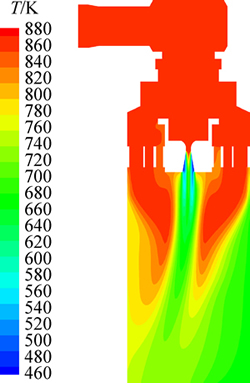
图5 高压蒸汽旁路阀截面温度场分布云图
Fig. 5 Temperature distribution on sectional in high-pressure steam bypass valve
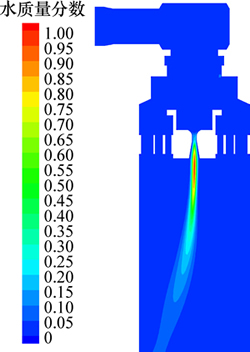
图6 高压蒸汽旁路阀截面减温水分布云图
Fig. 6 Distribution of desuperheating water mass fraction on sectional in high-pressure steam bypass valve
3 旁路阀阀体温度计算
3.1 阀体外壁热边界条件
阀门在正常工作条件下,阀体外部有保温层,以防止阀门热量散失。但考虑到保温材料脱落等极端条件对阀门温度场的影响,所以对阀体外部无保温时的温度场进行计算。
当阀体外没有保温层时,阀体外壁热量将以自然对流和辐射2种形式向外散失,阀体外壁总散热qt为
 (10)
(10)
式中:T1为阀体外壁温度,K;T2为空气温度,K,本文中取293 K;h为保温材料表面对流换热系数,W/(m2·K);ε0为表面发射率,本文取0.3。
由于计算热流密度要先知道阀体外表面温度T1,而阀体外表面温度T1为数值计算得到的结果。因此,采用迭代法计算,先假定阀体外表面温度T1,依据此温度计算阀体表面总散热热流密度,再计算阀体温度场,当阀体表面温度场与设定值一致时,计算结果为最终有效结果。本处省略迭代计算过程,仅得最终计算结果:空气温度为293 K;阀门下部接有管道,阀体与管道总长约为2 m,假设阀体外表面温度为780 K (根据后续计算,阀体表面平均温度为784 K)。
计算平均温度Tm为
 (11)
(11)
已知为536.5 K时空气物性参数如表1所示。
表1 536.5 K空气物性参数
Table 1 Physical parameters of air at 536.5 K

传质格拉晓夫数Gr表达式为
 (12)
(12)
式中:重力加速度g=9.8 m/s2;体积变化系数a=1/780 K-1;特征尺度l=2 m;△T=487 K;ν=40.61×10-6 m2/s代入式(12),可得Gr=2.97×1010,可知流动处于湍流状态。
此时努塞尔数Nu和对流换热系数h分别为
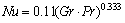 (13)
(13)
 (14)
(14)
将Gr=2.97×1010和Pr=0.677代入式(13)可得Nu=296;将Nu=296,λ=0.042 7 W/(m·K)和l=2 m代入式(14)可得h=6.33 W/(m2·K)。
因此,可得阀体外表面自然对流换热流密度qc=h(T1-T2)=3.082 kW/m2,辐射损失热量qr=σε(T14- T24)=6.166 kW/m2,则阀体外壁总散热qh=qc+qr= 9.248 kW/m2。
设ηc和ηr分别为阀体表面热损失中的自然对流换热损失率和辐射热损失率,则有:
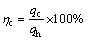 (15)
(15)
 (16)
(16)
由计算可知:在阀体表面热损失中,33%为自然对流换热损失,67%为辐射热损失。
3.2 阀体温度场数值计算结果
图7所示为阀体外表无保温层时阀体外壁温度分布云图。从图7可以看出:当阀体外表面无保温层时,阀体温差较大,温差为203 K左右,最高温为872 K,最低温为669 K。最低温度出现在阀体上端,这是由于此处蒸汽不流动所致。进一步计算得知,阀体表面平均温度为784 K,阀体表面总热损失为42.292 kW。
图8所示为阀中截面温度分布云图。从图8可以看出:阀体内壁温度与蒸汽温度接近,平均为868 K。阀体内外壁温度差异较大,内外壁温差最大值约为203 K,内外壁平均温差为80 K左右,这是没有外保温层下的计算结果,所以内外壁温度差较大。
图9所示为阀体内壁温度分布云图。由图9可知: 阀体内壁温度也代表着与阀体接触的蒸汽温度。阀体内壁上半部分平均温度为868 K,与蒸汽入口温度几乎相同。在阀顶端的温度较低,这是由于此区域蒸汽流速较低,在计算时又没有考虑阀体保温所形成的。与上半部分相比,阀体下半部分温度总体较低,平均温度为770 K左右,这是由于经过节流作用后蒸汽的压力下降,导致蒸汽温度有所下降。但由于蒸汽比热容较大,且流经阀门的蒸汽量较大,所以在阀体下半部分温度场分布总体较均匀。
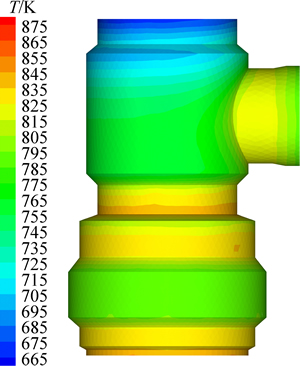
图7 阀体外表面温度分布云图
Fig. 7 Temperature distribution on surface of valve body
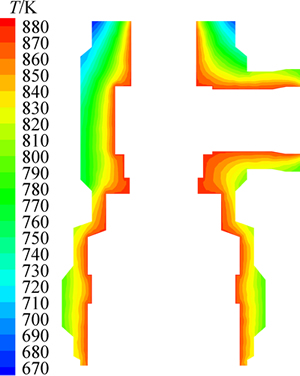
图8 阀体中截面温度分布云图
Fig. 8 Temperature distribution on section of valve body
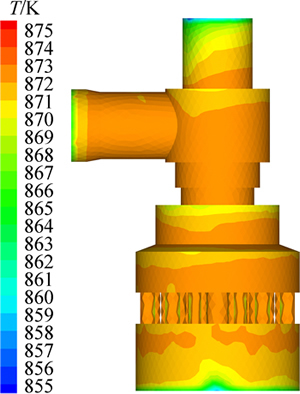
图9 阀体内壁温度分布云图
Fig. 9 Temperature distribution on inner wall of valve body
4 结论
1) 高压差下阀内流场速度整体较快,平均流速为10~30 m/s,其中最大流速出现在蒸汽与减温水喷嘴混合处,此处最大流速接近80 m/s,且阀内速度并不沿管道中轴线方向均匀分布,阀门出口处流体偏向于一侧。
2) 阀内温度场总体呈现出入口高、出口低的分布情况,蒸汽入口温度为870 K,出口平均温度为660 K,最低温度出现在拉伐尔喷管处,约为470 K。
3) 当阀体外表面无保温层时,阀体温差较大,为203 K,最高温度为872 K,最低温度为669 K。
参考文献:
[1] Dalitz F, Maiwald M, Guthausen G. Considerations on the design of flow cells in by-pass systems for process analytical applications and its influence on the flow profile using NMR and CFD[J]. Chemical Engineering Science, 2012, 75(25): 318-326.
[2] Tsai C W, Shih C, Wang J R, et al. On study of steam bypass and pressure control system for Lungmen nuclear power plant[J]. Procedia Engineering, 2011, 15: 5328-5332.
[3] Würdemann H, Westphal A, Lerm S, et al. Influence of microbial processes on the operational reliability in a geothermal heat store-results of long-term monitoring at a full scale plant and first studies in a bypass system[J]. Energy Procedia, 2014, 59: 412-417.
[4] WANG Weibing, WANG Xudong, LIU Dongju. IP start-up control for 300 MW turbine unit with bypass system[J]. Procedia Engineering, 2011, 16: 493-498.
[5] Pugi L, Galardi E, Carcasci C, et al. Preliminary design and validation of a real time model for hardware in the loop testing of bypass valve actuation system[J]. Energy Conversion & Management, 2015, 92: 366-384.
[6] Sang H Y, Lee J G, Suh K Y. Direct vessel inclined injection system for reduction of emergency core coolant direct bypass in advanced reactors[J]. Nuclear Engineering and Design, 2006, 236(22): 2329-2342.
[7] Krivopuskov D A. Computer technology for valve and accessory designers and manufacturers[J]. Chemical & Petroleum Engineering, 2005, 41(3): 211-214.
[8] 鄂加强, 李志鹏, 龚金科, 等. 新型双向旋球阀工作过程动力学仿真分析[J]. 湖南大学学报(自然科学版), 2010, 37(10): 25-29.
E Jiaqiang, LI Zhipeng, GONG Jinke, et al. Dynamic simulation and analysis of the work process of a new type rotating ball valve with double direction metal sealing[J]. Journal of Hunan University(Natural and Science Edition), 2010, 37(10): 25-29.
[9] 鄂加强, 李志鹏, 袁丁, 等. 新型双向硬密封旋球阀多学科设计优化[J]. 中南大学学报(自然科学版), 2010, 41(2): 45-52.
E Jiaqiang, LI Zhipeng, YUAN Ding, et al. Multidisciplinary optimization design on new type rotating ball valve with double direction metal sealing[J]. Journal of Central South University (Science and Technology), 2010, 41(2): 45-52.
[10] 雷吉平, 鄂加强, 陈健美. 新型双向硬密封大口径旋球阀性能实验分析[J]. 中南大学学报(自然科学版), 2013, 44(5): 1849-1854.
LEI Jiping, E Jiaqiang, CHEN Jianmei. Experimental analysis of seal performance for new-type large diameter rotating ball valve with bidirectional metal sealing[J]. Journal of Central South University (Science and Technology), 2013, 44(5): 1849-1854.
[11] ZHU Xiaoxiao, ZHANG Shimin, TAN Guibin, et al. Experimental study on dynamics of rotatable bypass-valve in speed control pig in gas pipeline[J]. Measurement, 2014, 47(1): 686-692.
[12] Rensburg N J V, Steyn J L, Els P S. Time delay in a semi-active damper: modelling the bypass valve[J]. Journal of Terramechanics, 2002, 39(1): 35-45.
[13] LANG Minggang, DONG Yujie. The ATWS analysis of one control rod withdraw out of the HTR-10GT core in addition with bypass valve failure[J]. Nuclear Engineering & Design, 2013, 271(6): 459-464.
[14] 郑海. 汽轮机高压旁路阀调节特性的研究以及噪音分析[D]. 兰州:兰州理工大学能源与动力工程学院, 2012: 1-51.
ZHENG Hai. Research of the regulating characteristics and noise analysis in turbine’s HP bypass valve[D]. Lanzhou: Lanzhou University of Technology. School of Energy and Power Engineering, 2012: 1-51.
[15] 钟世梁, 黄荣国, 许冰. 600 MW机组高压旁路减温减压阀热应力计算及寿命估算[J]. 动力工程学报, 2005, 25(2): 267-270.
ZHONG Shiliang, HUANG Rongguo, XU Bing. Calculation of thermal stress and life expectancy of attemperation and pressure reduction valve of a 600 MW power set’s high-pressure bypass[J]. Chinese Journal of Power Engineering, 2005, 25(2): 267-270.
[16] 郑坊平, 崔雄华, 王弘喆, 等. 超超临界600 MW机组高压旁路阀螺栓失效分析[J]. 热力发电, 2012, 41(8): 86-90.
ZHENG Fangping, CUI Xionghua, WANG Hongzhe, et al. Failure analysis for bolt of high pressure bypass valve in ultra supercritical 600 MW unit[J]. Thermal Power Generation, 2012, 41(8): 86-90.
[17] YANG Aimin, PU Junsheng, Wong C B. By-pass valve control to improve energy efficiency of pneumatic drive system[J]. Control Engineering Practice, 2009, 17(6): 623-628.
[18] 杨小琨, 许星, 李建刚. 汽轮机高压旁路阀门内漏的热经济性分析[J]. 汽轮机技术, 2012, 54(5): 365-367.
YANG Xiaokun, XU Xing, LI Jiangang. Analysis of thermal economy for inner leakage of steam turbine high-pressure bypass[J]. Turbine Technology, 2012, 54(5): 365-367.
(编辑 刘锦伟)
收稿日期:2015-03-10;修回日期:2015-05-13
基金项目(Foundation item):国家自然科学基金资助项目(51076061)(Project(51076061) supported by the National Natural Science Foundation of China)
通信作者:余建平,博士,副教授,从事流动传热数值模拟研究;E-mail:yujianping2000@126.com