DOI: 10.11817/j.issn.1672-7207.2019.03.025
混凝土结构三维非线性徐变效应分析方法
李世伟,杨永清,陈远久
(西南交通大学 土木工程学院,四川 成都,610031)
摘要:为准确分析混凝土结构在不同应力水平和多向受力状态下的徐变效应,首先,通过徐变泊松比提出复杂应力状态下的徐变预测模型;然后,以混凝土塑性损伤本构模型为基础,提出一种新的考虑混凝土徐变三维特性的非线性徐变效应分析模型,建立相应的数值分析方法,并结合有限元分析软件ABAQUS二次开发计算程序;最后,通过徐变试验验证方法的可靠性。研究结果表明:提出的分析模型计算方便,所得结果合理,能够适用于复杂应力状态下的线性及非线性徐变效应分析。
关键词:混凝土结构;三维徐变特性;非线性徐变;ABAQUS二次开发
中图分类号:U448.21+8;TU311.41 文献标志码:A 文章编号:1672-7207(2019)03-0704-08
3D nonlinear creep analysis method for concrete structures
LI Shiwei, YANG Yongqing, CHEN Yuanjiu
(School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)
Abstract: In order to exactly analyze creep effects of concrete structures at different stress levels and under multiaxial loadings, firstly, a prediction model of creep in complex stress states was proposed through creep Poisson’s ratio. Secondly, based on the concrete damage plasticity (CDP) model, a new nonlinear creep effect analysis model considering 3D characteristic was presented, and a corresponding numerical method was established and implemented into the ABAQUS secondary platform. Finally, the reliability of the method was shown by comparing the analytical results to the classical experimental results. The results show that the proposed analytical model is convenient to calculate and the obtained results are rational, and can be widely used in the analysis of linear or nonlinear creep effect in complex stress states.
Key words: concrete structures; 3D characteristic of creep; nonlinear creep; secondary development by ABAQUS
徐变是混凝土结构主要时变特性之一,对高铁大跨度桥梁结构行为有着重要影响。国内外研究表明,徐变是引起大跨径混凝土梁式桥超下挠的主要原因之一[1],而过大的下挠会影响高速行车的舒适性和安全性[2]。大量混凝土桥的徐变效应具有明显的非线性特征。非线性徐变是指当混凝土承受高水平应力时(大于0.4fc,fc为水平应力),徐变与应力之间表现出明显的非线性特征[3]。工程实践表明,大量混凝土桥梁服役过程中出现了不同程度的开裂病害[4],表明桥梁结构部分区域已经进入塑性状态,线性徐变理论已不再适用,为准确分析徐变效应,需要建立非线性徐变理论。对于非线性徐变理论,现有的研究方法主要有3类:一类是直接通过高应力下的单轴受力徐变试验,建立模拟徐变特性的流变模型,如HAN等[5];另一类是以低应力下的单轴徐变特性为基础,建立徐变应变和应力之间的非线性函数关系,间接反映高应力下的徐变特性,如HAMED等[6];还有一类是采用损伤力学的方法来建立高应力下混凝土的非线性徐变本构方程,如李兆霞等[7-8]。前2类方法均是从单轴常应力作用下的徐变试验出发,很难运用到复杂空间应力状态下的徐变效应分析;对于第2类方法,往往因影响徐变非线性的因素众多,使得假定的非线性函数形式比较复杂,在实际工程中应用较为困难,且其适用性还需进一步验证;第3类方法把非线性徐变产生的原因归结为高应力下材料损伤演化,同时应用也较为方便,但已有研究成果也存在一定不足,如文献[7]运用连续介质损伤力学建立了弹性徐变损伤分析模型,并未涉及材料塑性行为的影响,文献[8]运用经典的单轴应力应变关系(Hongnestad模型)探讨了混凝土非线性徐变效应的分析方法,而单轴应力应变曲线并不能完整地描述混凝土材料的非线性行为,也不能直接应用于复杂应力状态。另外,对于大型混凝土结构如大跨混凝土桥等,在自重及温度等其他荷载作用下,应力应变分布存在明显的空间特征,混凝土的徐变也具有明显的三维特性[9]。李法雄等[10-11]基于线性叠加原理,提出了不同的三维徐变效应的分析模型,但均是基于线性徐变理论。本文作者基于混凝土弹塑性损伤力学,综合考虑材料损伤演化和徐变效应的三维特性,建立普遍适用于混凝土结构不同应力水平和多向受力状态下的徐变效应分析方法,并通过试验结果验证方法的准确性和适用性。
1 三维非线性徐变效应分析模型
1.1 徐变效应三维特性的处理
对于如大跨混凝土桥等的混凝土结构而言,徐变具有明显的三维特性。但是,关于多轴不同应力水平作用下的徐变规律研究还不成熟,没有直接可供借鉴的预测模型,本文拟通过引入徐变泊松比的概念,把单轴徐变规律拓展到多轴应力状态下。
单轴应力下的徐变泊松比是指在轴向应力作用下,横向徐变与轴向徐变之比。在多轴应力状态下,不同主应力方向的泊松比还与应力状态有关[12]。黄国兴等[13]指出,3个主应力方向的徐变泊松比随主应力的不同组合而变化,可按下式计算:
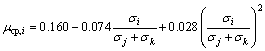 (1)
(1)
这样,即可建立考虑徐变泊松比影响的转换矩阵A:
 (2)
(2)
式中:μcp,i为主应力σi方向的徐变泊松比;i,j,k=1,2,3,且 。
。
1.2 三维非线性徐变本构关系
加载龄期为τ的混凝土结构,在t时刻的总应变首先应包括在龄期τ内的弹性应变及其徐变应变,其次是在(t-τ)时间段内应力增量引起的弹性应变及其对应的徐变应变,再次是收缩应变(εS)与温度应变(εT),因此,通过引入徐变泊松比影响矩阵,三维非线性徐变本构关系可表示为
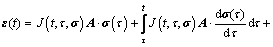
 (3)
(3)
式中:σ为应力分量矩阵, σ=[σx, σy, σz, σxy, σxz, σyz]T;ε为应变分量矩阵, ε=[εx, εy, εz, εxy, εxz, εyz]T;J(t, τ, σ)为当加载龄期为τ时,混凝土结构在t时刻的徐变函数,
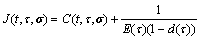 (4)
(4)
E(τ)为混凝土在加载时刻的弹性模量;d(τ)为τ时刻混凝土的损伤因子,其值在[0,1]之间,与混凝土应力状态有关;C(t, τ, σ)为用Dirichlet级数表达的徐变度函数,
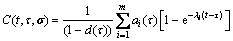 (5)
(5)
采用式(5)可方便地对不同的徐变预测模型进行拟合,且能避免对整个时间历程的应力历史进行积分。参数ai(τ)与λi的确定可按文献[10]提供的方法拟合。
1.3 时间步△ti徐变应变增量计算
对施工过程中经历了结构体系转换的桥梁结构而言,收缩产生的次内力还会引起相应的徐变变形,不仅如此,徐变变形产生的徐变次内力也会影响后续的徐变变形。在众多的分析方法中,基于逐步递推的分析方法能够较方便地处理这一复杂过程,且能与现有通用有限元程序相结合,因此,在实际工程中得到广泛应用[10-11]。本文提出的三维收缩徐变效应力学模型正是基于上述方法建立的。
由式(3)可知,tn和tn+1时刻的徐变应变εc可表示为
 (6)
(6)
△tn+1增量步内的徐变应变增量为
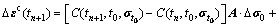
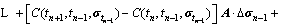
 (7)
(7)
式中:△σn为△tn增量步内的应力张量增量。
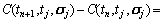
 (8)
(8)
将式(8)代入式(7)可得徐变应变增量:
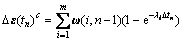 (9)
(9)
式中:ω(i, n)为递推关系矩阵,
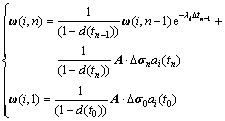 (10)
(10)
1.4 混凝土损伤演化
在混凝土的弹塑性分析中,混凝土本构关系对分析的效率和精度有着重要影响,本文选用ABAQUS提供的混凝土塑性损伤本构模型,该模型是由LUBLINER等[14]提出并经LEE等[15]改进的。该本构模型能够准确模拟混凝土在多种受力状态下的结构行为,且能反映受荷过程中混凝土材料的损伤演化,在工程界得到了广泛运用。其屈服(破坏)准则建立在有效应力空间上,表达式如下:
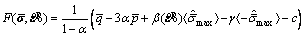 (11)
(11)
式中: 为等效净水压力;
为等效净水压力;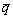 为等效Mises应力;
为等效Mises应力;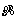 为等效塑性应变;
为等效塑性应变;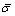 为有效应力张量;
为有效应力张量;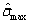 为有效应力特征值的最大值;c为混凝土黏聚力,与等效塑性应变
为有效应力特征值的最大值;c为混凝土黏聚力,与等效塑性应变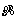 有关;
有关;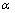 和β与混凝土双向和单向抗拉强度之比有关,γ为与混凝土三轴受压有关的系数,计算方法见文献[16];
和β与混凝土双向和单向抗拉强度之比有关,γ为与混凝土三轴受压有关的系数,计算方法见文献[16];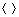 为Macaulay括号,定义为
为Macaulay括号,定义为 = (|x|+x)/2。
= (|x|+x)/2。
流动准则选用应用广泛的Drucker-Prager准则,其表达式如下:
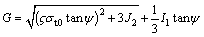 (12)
(12)
式中:ζ为偏心率,通常取0.1;σt0为混凝土单轴抗拉强度;J2为偏应力张量的第二不变量;ψ为混凝土塑性膨胀角。
根据弹塑性力学基本理论,塑性应变增量可表达为
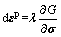 (13)
(13)
式中:λ为非负标量,εp为塑性应变。
实际应力和有效应力张量的之间的关系为
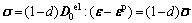 (14)
(14)
式中: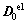 为初始刚度矩阵。
为初始刚度矩阵。
损伤因子d的表达式为
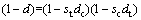 (15)
(15)
式中:dt和dc分别为混凝土拉伸损伤和压缩损伤,是等效拉伸塑性应变( )和等效压缩塑性应变(
)和等效压缩塑性应变(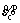 )的函数,
)的函数,
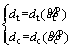 ,
, ,
, (16)
(16)
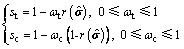 (17)
(17)
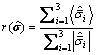 ,0≤
,0≤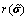 ≤1 (18)
≤1 (18)
式中: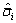 为等效应力张量的主应力;st和sc为损伤因子恢复函数,能够分别反映裂缝闭合效应和压缩损伤对抗拉强度的降低幅度;ωt和ωc为混凝土材料权重系数,分别控制应力方向时的拉、压刚度恢复;
为等效应力张量的主应力;st和sc为损伤因子恢复函数,能够分别反映裂缝闭合效应和压缩损伤对抗拉强度的降低幅度;ωt和ωc为混凝土材料权重系数,分别控制应力方向时的拉、压刚度恢复;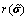 为应力权重因子。
为应力权重因子。
1.5 数值计算程序
根据前述的混凝土三维收缩徐变效应计算模型和数值分析方法,编制成FORTRAN语言嵌入到ABAQUS软件强大的二次开发功能,可以较方便地开发相应的计算程序。计算程序流程图如图1所示。
程序开发中的关键过程描述如下:在ABAQUS二次开发平台中,为实现徐变效应分析,将用到2个用户子程序(USDFLD和UEXPAN) 与1个功能子程序(GETVARM)。
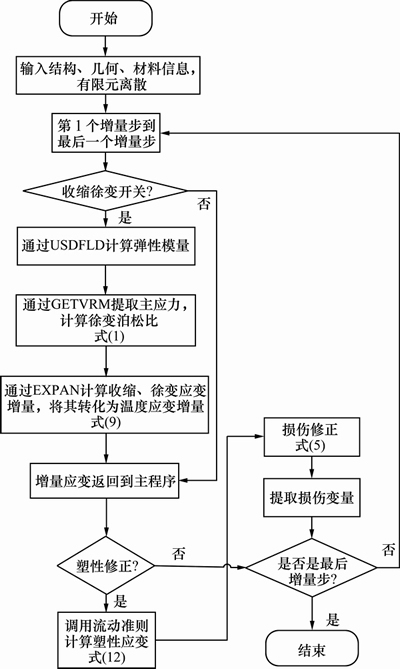
图1 收缩徐变效应计算程序流程图
Fig. 1 Shrinkage and creep effect computation program flow chart
子程序USDFLD的功能是实现混凝土弹性模量随龄期的演变。首先,在主程序中把弹性模量定义为参变量的函数;然后,在子程序USDFLD中指定每一时步的场变量。
子程序UEXPAN的功能是计算每一时步的收缩与徐变应变增量。在收缩应变增量的计算过程中,因为收缩应变与应力无关,可直接按照不同预测模型的计算方法计算。但对于徐变应变增量的计算,计算△tn时刻的徐变应变增量需要调用上一时步△tn-1计算的ω(i, n-1),如式(10)所示,因为相邻时步的徐变应变增量间存在递推关系。此时,需要定义解依赖的变量(SDVs)来储存每一时步的ω(i, n)。
功能子程序GETVARM被用来在每一时步调用材料积分点的变量,包括应力应变与解依赖的变量等,然后将其传递到子程序UEXPAN中。
子程序UEXPAN再把计算后的应变增量作为荷载返回到主程序中,调用混凝土塑性损伤分析模块进行材料非线性分析,完成塑性与损伤修正。通过3个子程序和主程序的相互协作,即可方便地实现混凝土结构的非线性徐变效应分析。
2 算例分析
2.1 算例一:钢管混凝土徐变试验
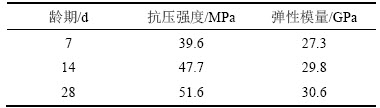
杨永清等[17]设计了自然环境下的钢管混凝土收缩徐变的试验装置,并获得了近3年的试验数据。试验用的混凝土强度等级为C55,配合比如表1所示。混凝土材料参数如表2所示。钢管采用A3钢,弹性模量为206 GPa。试验设置了3个圆柱体试件,柱体核心混凝土直径为259 mm,钢管壁厚为7 mm,高为600 mm。钢管混凝土徐变试验加载装置如图2所示。试件加载龄期为7 d。混凝土应变测点在试件中心,加载荷载为1 359.28 kN。
表1 C55混凝土配合比(密度)
Table 1 Mix proportion of concrete C55 kg/m3

表2 钢管混凝土材料参数
Table 2 Material parameters of concrete filled steel tube
对于钢管混凝土的收缩徐变而言,混凝土的收缩会受到钢管约束,核心混凝土因而受拉,产生拉伸变形和相应的徐变变形;同时,核心混凝土因受压产生的压缩徐变变形使得一部分原由核心混凝土承担的荷载向钢管转移。因此,为准确分析钢管混凝土的收缩徐变效应,需分别对钢管和混凝土进行有限元离散。选用ABAQUS软件对结构进行有限元分析,混凝土采用实体单元C3D8,核心混凝土共计3 840个单元;钢管采用实体单元C3D8I共计960个单元;钢管与混凝土交界面法向采用“硬接触”模拟,切向采用摩擦罚函数模拟,界面摩擦因数取0.25。假定垫板为不变形刚体,垫板与钢和混凝土的连结采用绑定约束,以保证加载过程中接触面不出现错动。钢管混凝土有限元模型如图3所示。
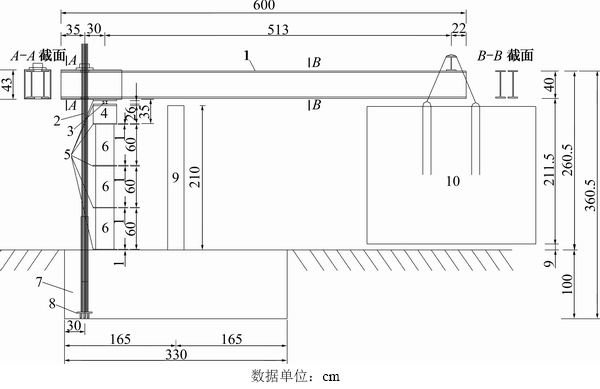
图2 钢管混凝土徐变试验加载装置
Fig.2 Creep test apparatus of concrete filled steel tube

图3 钢管混凝土有限元模型网格
Fig. 3 Finite element mesh model of concrete filled steel tube
混凝土构件理论厚度对收缩徐变的规律有重要影响[18],对于常见的预测模型,均把混凝土试件的理论厚度定义为试件体积与大气环境接触的面积的比值,如美国AASHTO LFRD[19]和JTG D62—2004[20]等,但上述规定对于钢管混凝土试件而言,明显是不合适的,因核心混凝土几乎不与大气环境接触,按上述定义计算的理论厚度趋近于无穷大。为此,本文选用美国西北大学Bazant教授提出的收缩徐变预测B3模型[21]和B4模型[22],因为这2个模型考虑因素较为全面,具有较高的精度[23-24];而且这2个模型均把徐变分为干燥徐变与基本徐变,而理论厚度只与干燥徐变有关。对于本试验的模拟不计干燥徐变,即认为核心混凝土不与外部环境发生湿度交换。因混凝土自生水化反应会消耗一部分水分,根据文献[25]中水化耗湿实验结果,本文选择核心混凝土湿度为85%。混凝土应变的实测值与模型计算值如图4所示。
分析结果表明,B4模型因考虑添加剂、掺合料和混凝土自收缩的影响,其应变预测值与实测值更接近,最大相对误差为-5.06%。
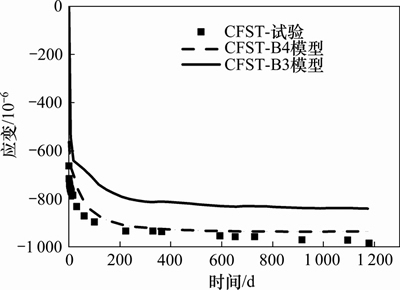
图4 钢管混凝土徐变应变计算曲线
Fig. 4 Calculated creep strain curves of concrete filled steel tube
2.2 算例二:混凝土简支梁非线性徐变试验
通过混凝土简支梁非线性徐变试验验证本文提出的徐变分析模型在混凝土材料进入非线性后的适用性。
GILBERT等[26]设计了不同水平应力水平下的混凝土简支梁徐变试验。试验混凝土简支梁结构长×宽×高为350 cm×34 cm×25 cm,受拉侧布置2根直径为16 mm钢筋,钢筋保护层厚度4 cm。混凝土简支梁材料参数如表3所示。模型在养护14 d后开始加载。实验梁采用集中荷载方式布载,加载方案如图5所示,其中,B1-a梁加载集中力为18.6 kN(0.5倍极限承载能力),B1-b梁加载集中力为11.8 kN(0.3倍极限承载能力)。
表3 混凝土简支梁材料参数
Table 3 Material parameters of concrete

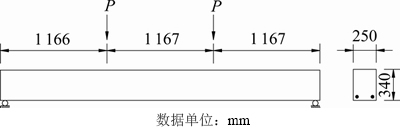
图5 混凝土简支梁徐变试验加载装置
Fig. 5 Creep test apparatus of concrete beams
因报告中并未给出混凝土配合比等相关资料,但提供了14 d龄期的收缩徐变实测试验结果,据此可对其收缩徐变规律进行数据拟合,选用Dirichlet函数进行拟合,拟合后与试验结果的对比如图6所示。
同样,采用ABAQUS软件对试验构件进行离散,混凝土采用实体单元C3D8,共计2 520个;钢筋选用桁架单元T3D2,共计120个,如图7所示。选用混凝土塑性损伤本构模型考虑材料非线性,参数设置如表4所示。模型开裂分析与裂缝实测对比如图8所示,线性徐变理论(L)、非线性徐变理论(NL)计算值与实测值的对比如图9所示。
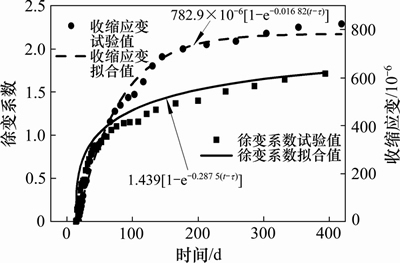
图6 收缩徐变试验值与拟合函数曲线
Fig. 6 Experimental data and fitting curves of shrinkage and creep
分析结果表明:对于开裂情况而言,数值模拟的裂缝开展情况与试验结果大致吻合;对于跨中截面长期下挠而言,B1-a和B1-b试验梁实测初始下挠分别为4.9 mm和2.1 mm,最终变形分别为12.1 mm和7.5 mm;当采用线性徐变理论时,B1-a和B1-b试验梁初始下挠分别为2.2 mm和1.4 mm,最终变形分别为4.8 mm和3.8 mm,均远小于实测值;而当考虑材料非线性时,B1-a和B1-b试验梁初始下挠分别为6 mm和2.1 mm,最终变形分别为11.7 mm和8.1 mm,与实测值更为接近,长期下挠相对误差分别为-3.5%和8.3%。

图7 混凝土简支梁有限元模型网格
Fig. 7 Finite element mesh model of concrete beams
表4 混凝土简支梁塑性损伤模型参数设置
Table 4 Parameter setting of CDP
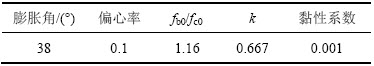
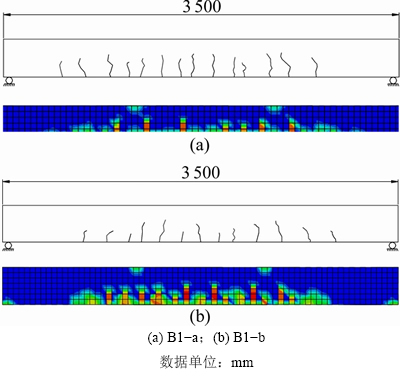
图8 裂缝分析结果对比
Fig. 8 Comparison of FEM and experimental crack pattern
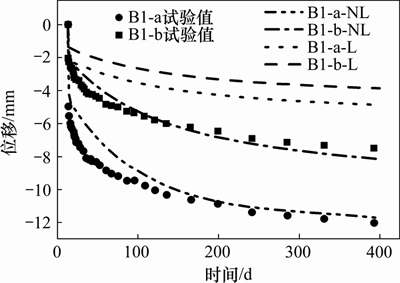
图9 试验梁跨中截面长期变形试验值与计算值比较
Fig. 9 Comparison of FEM and experimental results of time-dependent mid-span deflections
3 结论
1) 提出了一种新的三维非线性徐变效应分析模型,综合考虑了徐变效应的三维特性和材料损伤演化的影响,并提出了相应的数值分析方法。
2) 以大型通用有限元软件ABAQUS为平台,基于FORTAN语言二次开发了分析程序。算例验证结果表明,计算结果可靠,能够广泛适用于复杂应力状态下的混凝土结构线性及非线性徐变效应分析。
3) 对于存在开裂、超下挠等病害的混凝土结构长期结构行为分析,需要建立非线性徐变理论。
4) 对于多轴应力状态下的混凝土徐变预测研究尚不成熟。通过引入徐变泊松比,把单轴受力徐变规律拓展到复杂应力状态下,与实际的徐变规律存在一定偏差,相关问题尚需进一步研究。
参考文献:
[1] BAZANT Z P, HUBLER M H, YU Q. Pervasiveness of excessive segmental bridge deflections[J]. ACI Structural Journal, 2011, 108(6): 766-774.
[2] 翟婉明, 赵春发, 夏禾, 等. 高速铁路基础结构动态性能演变及服役安全的基础科学问题[J]. 中国科学:技术科学, 2014, 44(7): 645-660.
ZHAI Wanming, ZHAO Chunfa, XIA He, et al. Basic scientific issues on dynamic performance evolution of the high-speed railway infrastructure and its service safety[J]. Scientia Sinica Technologica, 2014, 44(7): 645-660.
[3] LI Z X, QIAN J C. Creep damage analysis and its application to nonlinear creep of reinforced concrete beam[J]. Engineering Fracture Mechanics, 1989, 34(4): 851-860.
[4] 文武松. 大跨度PC连续刚构桥挠曲开裂因素研究[D]. 成都: 西南交通大学土木工程学院, 2009: 22-35.
WEN Wusong. Study on reason and regularity of cracking and increasing of deflection for long span pc continuous rigid frame bridge [D]. Chengdu: Southwest Jiaotong University. School of Civil Engineering, 2009: 22-35.
[5] HAN B, XIE H, ZHU L, et al. Nonlinear model for early age creep of concrete under compression strains[J]. Construction and Building Materials, 2017, 147: 203-211.
[6] HAMED E. Modelling of creep in continuous RC beams under high levels of sustained loading[J]. Mechanics of Time-dependent Materials, 2014, 18(3): 589-609.
[7] 李兆霞, 钱济成. 混凝土徐变损伤演变方程及其在非线性徐变理论中的应用[J]. 河海大学学报, 1989, 17(2): 26-34.
LI Zhaoxia, QIAN Jicheng. An evolution equation for creep damage and its application to nonlinear creep of concrete[J]. Journal of Hohai University, 1989, 17(2): 26-34.
[8] 黄海东, 向中富. 混凝土结构非线性徐变计算方法研究[J]. 工程力学, 2014, 31(2): 96-102.
HUANG Haidong, XIANG Zhongfu. Nonlinear creep analysis method for concrete structures[J]. Engineering Mechanics, 2014, 31(2): 96-102.
[9] KIM J K, KWON S H, KIM S Y, et al. Experimental studies on creep of sealed concrete under multiaxial stresses[J]. Magazine of Concrete Research, 2005, 57(10): 623-634.
[10] 李法雄. 组合梁斜拉桥空间受力行为及时变效应[D]. 北京: 清华大学土木水利学院, 2011: 144-168.
LI Faxiong. Spatial structural behavior and time-dependent analysis of composite cable stayed bridge[D]. Beijing: Tsinghua University. School of Civil Engineering, 2011: 144-168.
[11] 黄海东, 向中富, 郑皆连. PC箱梁桥三维徐变效应精细化分析[J]. 中国公路学报, 2013, 26(5): 108-114.
HUANG Haidong, Xiang Zhongfu, Zheng Jielian. Experimental study and prediction model for concrete creep in ambient environment[J]. China Journal of Highway and Transport, 2013, 26(5):108-114.
[12] MAZZOTTI C, SAVOIA M. Nonlinear creep, Poisson's ratio, and creep-damage interaction of concrete in compression[J]. ACI Materials Journal, 2002, 99(5): 450-457.
[13] 黄国兴, 惠荣炎, 王秀军. 混凝土徐变与收缩[M]. 北京: 中国电力出版社, 2012: 52-55.
HUANG Guoxing, HUI Rongyan, WANG Xiujun. Creep and shrinakge of concrete[M]. Beijing: China Electric Power Press, 2012: 52-55.
[14] LUBLINER J, OLIVER J, OLLER S. A plastic-damage model for concrete[J]. International Journal of Solids and Structures, 1989, 25(3): 299-326.
[15] LEE J, FENVES G L. Plastic-damage model for cyclic loading of concrete structures[J]. American Society of Civil Engineers, 1998, 124(8): 892-900.
[16] 秦浩, 赵宪忠. ABAQUS混凝土损伤因子取值方法研究[J]. 结构工程师, 2013, 29(6): 27-32.
QIN Hao, ZHAO Xianzhong. Study on the ABAQUS damage parameter in the concrete damage plasticity model[J]. Structural Engineers, 2013, 29(6): 27-32.
[17] 杨永清, 鲁薇薇. 自然环境下钢管混凝土收缩徐变试验研究报告[R]. 成都: 西南交通大学土木工程学院, 2012: 25-48.
YANG Yongqing, LU Weiwei. Experimental study on creep and shrinkage of CFST under ambient environment[R]. Chengdu: Southwest Jiaotong University. School of Civil Engineering, 2012: 25-48.
[18] 王永宝, 赵人达, 徐腾飞,等. 钢管混凝土轴压构件徐变简化计算方法研究[J]. 公路交通科技, 2016, 33(1): 57-63.
WANG Yongbao, ZHAO Renda, XU Tengfei, et al. Study on simplified creep calculation method of CFST members under axial loading[J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 57-63.
[19] LRFDUS—5, AASHTO LRFD bridge design specifications(5th ed)[S].
[20] JTG D62—2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].
JTG D62—2004, Code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S].
[21] BAZANT Z P. Creep and shrinkage prediction model for analysis and design of concrete structures-model B3[J]. Materials and Structures, 1996, 29(2): 126-126.
[22] BAZANT Z P, WENDNER R. RILEM draft recommendation: TC-242-MDC multi-decade creep and shrinkage of concrete: material model and structural analysis[J]. Materials & Structures, 2015, 48(4): 753-770.
[23] 丁文胜, 吕志涛, 孟少平, 等. 混凝土收缩徐变预测模型的分析比较[J]. 桥梁建设, 2004(6): 13-16.
DING Wensheng, LU Zhitao, MENG Shaoping, et al. Analysis and comparison of prediction models for concrete shrinkage and creep[J]. Bridge Construction, 2004(6): 13-16.
[24] AL-MANASEER A, PRADO A. Statistical comparisons of creep and shrinkage prediction models using RILEM and NU-ITI databases[J]. ACI Materials Journal, 2015, 112(6): 829-831.
[25] ZHANG J, WANG J H, GAO Y. Moisture movement in early ages concrete under cement hydration and environmental drying[J]. Magazine of Concrete Research, 2016, 68(8): 391-408.
[26] GILBERT R, NEJADI S. An experimental study of flexural cracking in reinforced concrete members under sustained loads[D]. Sydney: The University of New South Wales. School of Civil and Environmental Engineering, 2004: 1-18.
(编辑 赵俊)
收稿日期:2018-05-26;修回日期:2018-08-04
基金项目(Foundation item):铁道部科技研究开发计划重大课题资助项目(2008G031-K) (Project(2008G031-K) supported by the Major Program of Technological Research and Development of China Railway Ministry)
通信作者:杨永清,博士,教授,从事大跨径混凝土桥结构行为研究;E-mail:yangyongqingx@163.com