电流模式控制Buck-Boost变换器建模及非线性现象仿真
袁雷,沈建清,肖飞
(海军工程大学 舰船综合电力技术国防科技重点实验室,湖北 武汉,430033)
摘要:根据电流模式控制下Buck-Boost变换器的工作特性,建立变换器的统一数学模型,并基于Matlab/Simulink仿真软件,分别搭建工作于电流连续和电流断续模式下变换器的仿真模型。通过对电流连续模型进行仿真,揭示参考电流Iref和电感L在不同的工作情况下出现倍周期分叉并最终导致混沌的现象;对电流断续模型进行仿真,得出以输入电压E变化时的混沌相图,验证电流断续模式下混沌现象的存在性。同时为消除这2种模式下的混沌现象,引入PID控制器。仿真结果表明:通过设置适当的参数,可以有效地抑制变换器中的混沌现象。
关键词:Buck-Boost变换器;建模;电流连续模式;电流断续模式:PID控制器;混沌
中图分类号:TM46 文献标志码:A 文章编号:1672-7207(2012)03-0972-08
Modeling and nonlinear phenomena simulation of current-mode controlled Buck-Boost converter
YUAN Lei, SHEN Jian-qing, XIAO Fei
(National Key Laboratory of Vessel Integrated Power System Technology, Naval University of Engineering, Wuhan 430033, China)
Abstract: According to the working characteristics of current-mode controlled Buck-Boost converter, the uniform mathematic model of converter was set up, two simulation models of converter worked in continuous conduction mode (CCM) and discontinuous conduction mode (DCM) was built by employing Matlab/Simulink soft. The simulation results were gained by using the two kinds of models. In the CCM model, the phenomenon of bifurcation and chaos were obtained with resistance L and reference current Iref varying; in DCM model, the phase diagrams were obtained by changing input voltage E, which proved the existence of chaotic phenomena. A PID controller was applied to eliminate the chaos phenomena in two models. All simulation results demonstrate that the chaos phenomena can be restrained by choosing appropriate parameters of PID controller.
Key words: Buck-Boost converter; model; continuous conduction mode (CCM); discontinuous conduction mode (DCM); PID controller; chaos
DC-DC开关变换器一般由Buck,Boost和Buck-Boost等基本电路演化而成,其本质上是一种非线性电路系统,在实际运行过程中,时常会出现次谐波、分叉及混沌等一些奇异或者不规则现象[1-8],从而导致系统的状态无法预测和控制。目前,对于Buck-Boost变换器中存在的非线性现象的研究主要集中在电流连续的模式下(CCM)[9-12],并且验证了变换器中存在的非线性现象,但是却没有提出消除混沌现象的控制方案。而更有广泛意义的不连续运行模式(DCM)的研究却很少,然而从理论展开分析研究往往又比较复杂[13-14]。本文作者借助Matlab/Simulink分别搭建了CCM和DCM模式下的Buck-Boost变换器的仿真模型,得到的仿真结果直观易懂,从而验证了在CCM和DCM模式下均存在混沌现象的结论。同时设计了PID控制器,通过恰当的参数选择,可以较好地抑制变换器中存在的混沌现象。另外,搭建的仿真模型中参数易于调整,对变换器的参数设计具有一定的指导意义。
1 Buck-Boost变换器建模
电流模式控制Buck-Boost变换器是以电流为控制对象的DC-DC变换器,它既能实现升压变换又可实现降压变换,其电路原理如图1所示,其中切换开关S由RS触发器和比较器组成反馈电路控制。
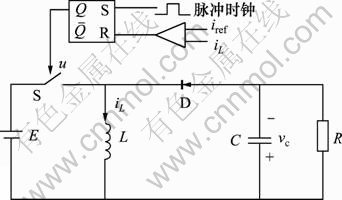
图1 电流模式控制Buck-Boost变换器电路原理图
Fig.1 Circuit diagram of current-mode controlled Buck-Boost converter
其工作原理是:当时钟脉冲开始后(Q=1)切换开关S导通,则电感电流iL线性增加,当iL增加至峰值参考电流Iref时,触发器复位(Q=0),导致切换开关S关断,电感L与输出部分RC产生谐振,使得iL下降,直至下一个时钟脉冲到来时,触发RS触发器使开关S闭合,iL又开始线性增加,从而变换器完成一个周期的相位切换。根据电感电流iL连续与否,Buck-Boost变换器有电流连续和电流断续2种工作模式,即CCM和DCM模式。
1.1 CCM模式下的建模
建立微分方程时分别以电感电流iL和电容电压vc作为状态变量。在CCM模式下,只有切换开关S闭合与关断2种状态,根据KCL与KVL定律列写其微分方程[15]。
(1) 开关S闭合,二极管D截止,其微分方程为:
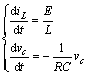 (1)
(1)
其中:E为直流侧电源电压;R为电阻;L为电感;C为电容。
(2) 开关S关断,二极管D导通,其微分方程为:
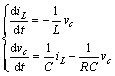 (2)
(2)
根据电流模式控制Buck-Boost变换器和RS触发器的工作原理,当电感电流iL大于参考电流Iref时,触发器R端的逻辑值为1,同时S端接收时钟脉冲,使得Q端的逻辑值为1,切换开关闭合;相反Q端的逻辑值为0,切换开关关断。因此,RS触发器Q端的输出逻辑值1或0用来控制切换开关的脉宽调制信号u,即:
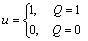 (3)
(3)
根据切换开关S的控制信号u的不同,可得到Buck-Boost变换器的统一微分方程:
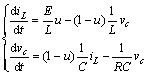 (4)
(4)
在Matlab/Simulink环境下,根据式(4)搭建Buck- Boost变换器的分段开关模型如图2所示。
在该模型中,采用时钟脉冲发生器(Pulse generator)为RS触发器的S端提供脉冲信号,且幅值为1,采样周期t=50 ms;同时为了给触发器的R端提供逻辑值1或0,该模型使用Sign模块,其作用是:当电感电流iL>Iref时,该信号模块输出为1,通过运算放大器缩小0.5倍可以产生触发器R端所需要的逻辑值1;相反,当iL<Iref时,该信号模块输出为-1,从而产生触发器R端所需要的逻辑值0。
1.2 DCM模式下的建模
在DCM模式下,切换开关S闭合和关断电感电流连续时的微分方程同式(1)和(2),仅增加了切换开关S关断和二极管D截止时的状态,其电感电流断续时的微分方程为:
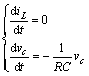 (5)
(5)
根据微分方程式(4)和(5)建立电流模式控制Buck-Boost变换器电流断续仿真模型如图3所示。
在DCM模式下,该模型采用2个Switch开关模块来模拟控制器件,并且为了模拟可控制器件关断时电流连续和断续模式,引入了一个关系判断模块(Relational operator),以实现对其模块输入端的比较,将它设计为“>”,并将电感电流和0作为其输入,其工作原理为:当电感电流iL>0时,输出为1,其工作在CCM模式下;相反,iL<0时,输出为0,其工作在DCM模式下,从而可以实现Buck-Boost变换器在CCM和DCM模式下的切换。

图2 CCM下电流模式控制Buck-Boost变换器仿真模型
Fig.2 Simulation model of Buck-Boost converter in CCM
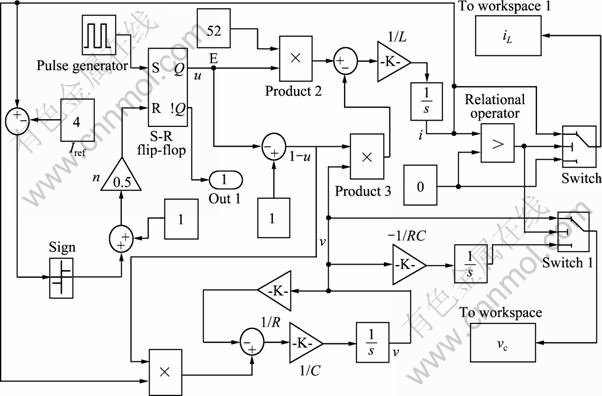
图3 DCM下电流模式控制Buck-Boost变换器仿真模型
Fig.3 Simulation model of Buck-Boost converter in DCM
2 仿真结果分析
2.1 CCM模式下的仿真分析
为了说明本文所提建模方法的准确性,采用Matlab建立如图1所示的电路原理图,选取SimPowerSystems工具箱中的直流电源、电感、电容、二极管和IGBT开关器件,所得仿真结果与本文所提建模方法的仿真结果相比较。
在本小节仿真中,主要考虑参考电流Iref和电感L变化时变换器相图的变化情况。仿真结果中相图是以输出电压vc作为横坐标,以电感电流iL作为纵坐标。并且当改变电路中某一参数时,其他参数保持不变,同时得出的仿真结果均已舍去了瞬态过程,仅仅保留稳态值。
2.1.1 参考电流Iref变化时的仿真结果
在Buck-Boost变换器中,选取电路参数为[10]:输入电压E=20 V,电感L=0.5 mH,电容C= 4 mF,电阻R=20 W,开关周期t=50 ms。考虑参考电流Iref变化时变换器相图的变化情况,其仿真结果如图4所示。从图4可以看出:当Iref由小到大变化时,电压-电流相图由稳定经过倍周期分叉直至进入混沌状态的过程。当Iref=2.5 A时发生了2倍周期分叉(图4(b)),而且比较图4(b)和4(c)可以发现:在Iref分别为2.5 A和2.8 A时,相图中的极限环大小却不一样,这是由于随着参考电流Iref的增加,吸引子的尺寸越来越大的表 现[3]。图5所示为使用电路原理图1时Iref=4 A的混沌相图。由图5可知:与使用电路原理图1时Iref=4 A的混沌相图相比,相图完全一致,从而说明建模方法的正确性。由于参考电流Iref的变化会使输出发生倍周期分叉后过渡到混沌状态,恶化了变换器的工作性能。如何消除混沌现象以达到对输出电压的控制,显得尤为重要。PID控制参数易于调节,具有较强的鲁棒特性,在工程上也易于实现,并且通过选取适当的参数也可以实现混沌控制[16]。本文选取PID控制器如下:

图4 参考电流Iref变化时的相图
Fig.4 Phase diagrams with current Iref

图5 使用电路原理图1时Iref=4 A的混沌相图
Fig.5 Phase diagrams with current Iref=4 A by using circuit diagram 1
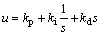 (6)
(6)
其中:kp,ki和kd为PID控制的调节参数。
将PID控制器式(6)加入如图2所示的CCM下电流模式控制Buck-Boost变换器仿真模型中,参数可设计为:kp=3.5,ki=3,kd=10。得到输出电压和电流的变化曲线如图6所示。从图6可以看出,电压和电流的混沌现象消除了,得到了比较平滑的变化曲线。
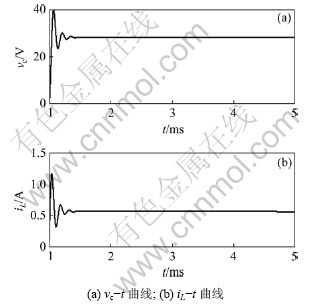
图6 加入PID控制后Iref=4 A时电压和电流变化曲线
Fig.6 Curves of output voltage and current when Iref=4 A by using PID controller
2.1.2 电感L变化时的仿真结果
选取电路参数为[10]:输入电压E=12 V,电容C= 2 mF,电阻R= 20 W,开关周期t= 50 ms,参考电流Iref=1.7 A。
利用如图2所示的仿真模型进行仿真,通过多次仿真发现:当L=0.01~0.07 mH时,电路工作在稳定的周期状态;随着电感L的不断增加,系统输出不再稳定,开始出现倍周期分叉并最终导致混沌的现象,当L=1.5 mH时系统开始出现混沌现象,如图7所示。图8所示为使用电路原理图1时电感L=1.5 mH的混沌相图。由图8可知:同样与使用电路原理图1时电感L=1.5 mH的混沌相图相比,相图基本一致,从而说明该建模方法的正确性。
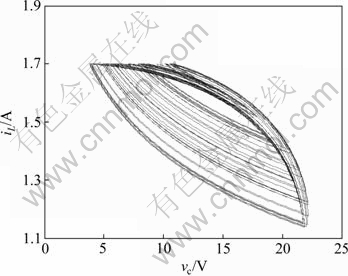
图7 电感L=1.5 mH时混沌相图
Fig.7 Phase diagram with resistance L=1.5 mH
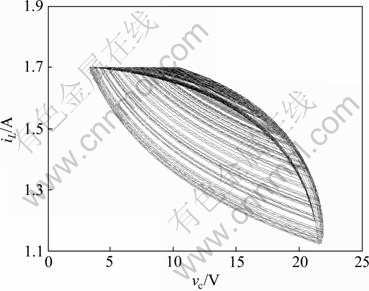
图8 使用电路原理图1时电感L=1.5 mH的混沌相图
Fig.8 Phase diagram with resistance L=1.5 mH by using circuit diagram 1
为了消除参考电流变化引起的混沌现象,同样采用PID控制器,且参数设置相同,得到如图9所示的变化曲线。从图9可以看出,电压和电流的混沌现象得到了消除。
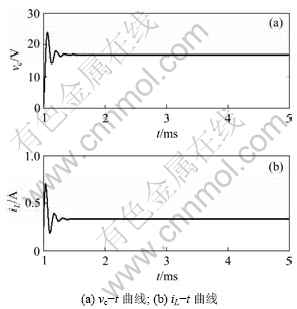
图9 加入PID控制后电感L=1.5 mH时电压和电流变化曲线
Fig.9 Curves of output voltage and current with L=1.5 mH by using PID controller
2.2 DCM模式下的仿真分析
选取电路参数为[11]:电感L=0.3 mH,电容C= 4 mF,电阻R=40 W,开关周期t=50 ms,参考电流Iref= 4 A。
为了验证在DCM工作模式下仍然存在混沌现象,本小节选择了变换器的输入电压E作为变换参数,仿真结果验证了混沌现象的存在性,同时也显示了比电流连续模式下更为复杂的变化规律,仿真结果如图10所示。
当E=55~46 V时,通过多次仿真发现电路工作在稳定的周期状态,如图10(a)所示;随着输入电压E的不断减少,变换器电路表现出不稳定性,当E=45V左右时相图中出现了2倍周期分叉的相图(图10(b));当E=30 V左右时则出现了4倍周期分叉的相图(图10(c));当E=10.5 V时电路开始出现混沌现象(图10(d))。相轨迹的底面是平的,对应的电流均为0 A,反映了电感电流断续的特点。
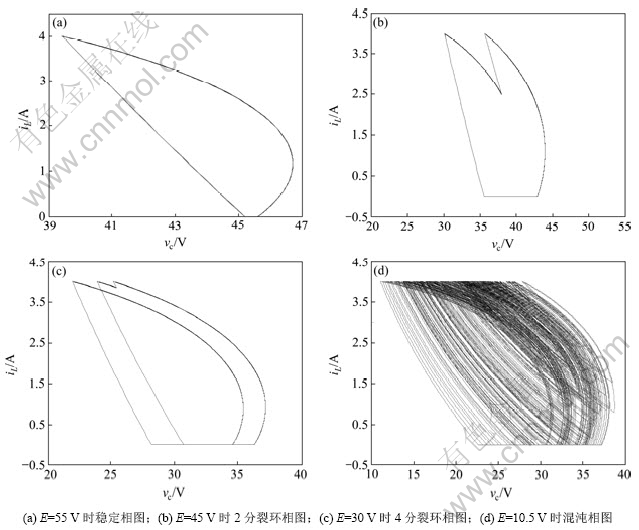
图10 输入电压E变化时相图
Fig.10 Phase diagrams with input voltage E
为了消除电压E的变化所引起的混沌现象,同样将PID控制器式(6)加入如图3所示的DCM下电流模式控制Buck-Boost变换器仿真模型中,参数可设计为:kp=1.6,ki=3,kd=8。从而得到输出电压和电流的变化曲线,如图11所示。从图11可以看出:输出电压和电流的混沌现象消除了,得到了比较平滑的变化曲线。
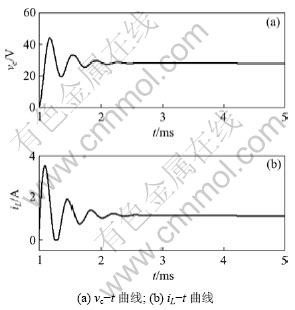
图11 加入PID控制后E=10.5 V时电压和电流变化曲线
Fig.11 Curves of output voltage and current with E=10.5 V by using PID controller
仿真结果表明,当系统参数确定后,在DCM模式下,输入电压E直接影响变换器的运行性能和混沌现象的影响,从而表明在实际应用中加入PID控制器,通过设置适当的参数可以有效地消除混沌现象。
3 结论
(1) 分析了电流模式控制Buck-Boost变换器和RS触发器的基本工作原理,将触发器Q端输出的逻辑值作为切换开关的控制信号,得到了CCM模式下的统一微分方程。
(2) 利用Matlab/Simulink的强大功能分别搭建了CCM和DCM模式下的仿真模型,仿真结果验证了变换器模型的正确性及建模方法的可行性。
(3) 在CCM模式下,揭示了参考电流Iref和电感L在不同的工作情况下出现混沌的现象,甚至取不同的电阻R和电容C同样会产生混沌现象,限于篇幅本文没有把结果一一列出;在DCM模式下,以输入电压E作为参考值分析了混沌现象的产生。同时为了消除变换器中混沌现象而引入的PID控制器,参数调整简单,易于在工程中实现。
参考文献:
[1] Tsec C K, Bernardo M D. Complex behavior in switch power converters[J]. Proceeding of the IEEE, 2002, 90(5): 768-781.
[2] 周宇飞, 陈军宁. 电流模式控制Boost变换器中的切分叉及阵发混沌现象[J]. 中国电机工程学报, 2005, 25(1): 23-26.
ZHOU Yu-fei, CHEN Jun-ning. Tangent bifurcation and intermittent chaos in current-mode controlled Boost converter[J]. Proceeding of the CSEE, 2005, 25(1): 23-26.
[3] Bernado M D, Vasca F. Discrete-time maps for the analysis of bifurcations and chaos in DC/DC converter[J]. IEEE Transactions on Circuits and Systems: Ⅰ, 2000, 47(2): 130-143.
[4] 周宇飞, 姜丹丹, 黄家成, 等. DC-DC 变换器中负载阻抗特性及其对稳定性的影响[J]. 中国电机工程学报, 2010, 30(6): 15-21.
ZHOU Yu-fei, JIANG Dan-dan, HUANG Jia-cheng, et al. Impedance characteristic of load in DC-DC converters and its effect on stability[J]. Proceeding of the CSEE, 2010, 30(6): 15-21.
[5] Wu X, Tse C K, Dracga O, et al. Fast-scale instability of the voltage-mode DC-DC converters[J]. IEEE Transactions on Circuits and Systems:Ⅰ, 2006, 53(1): 204-213.
[6] Banerjee S, Parui S, Gutpa A. Dynamical effects of missed switching in current-mode controlled dc-dc converters[J]. IEEE Transactions on Circuits and Systems:Ⅱ, 2004, 51(12): 649-654.
[7] 江伟, 周宇飞, 陈军宁, 等. 基于逻辑变量化简方法的Boost变换器建模与分析[J]. 系统仿真学报, 2011, 23(2): 409-413.
JIANG Wei, ZHOU Yu-fei, CHEN Jun-ning, et al. Modeling and analysis of Boost converter based on method of logic variable simplification[J]. Journal of System Simulation, 2011, 23(2): 409-413.
[8] 王开艳, 王春芳, 张玲丽. CCM和DCM模式Buck变换器建模与混沌现象仿真[J]. 系统仿真学报, 2008, 20(14): 3881-3884.
WANG Kai-yan, WANG Chun-fang, ZHANG Ling-li. Modeling and chaotic phenomena simulation of Buck converter in CCM and DCM[J]. Journal of System Simulation, 2008, 20(14): 3881-3884.
[9] WU Jie, LIU Ming-jian, YANG Ping. Study of bifurcation and chaos in the current-mode controlled Buck-Boost DC-DC converter (Ⅱ)—— Numerical analysis and experiment[J]. Control Theory and Applications, 2002, 19(3): 395-401.
[10] WU Jie, LIU Ming-jian, YANG Ping. Study of bifurcation and chaos in the current-mode controlled Buck-Boost DC-DC converter (Ⅰ) —— Modeling and simulation[J]. Control Theory and Applications, 2002, 19(3): 387-394.
[11] 李小峰, 戴栋, 马西奎. 不连续运行模式电流型Buck-Boost变换器中的分叉和混沌[J]. 西安交通大学学报, 2003, 37(8): 800-803.
LI Xiao-feng, DAI Dong, MA Xi-kui. Bifurcation and chaos from a current-programmed Buck-Boost converter operating in discontinuous mode[J]. Journal of Xi’an Jiao Tong University, 2003, 37(8): 800-803.
[12] WANG Li-qing, WEI Xue-ye, WEN Wei-gang. Computer simulation based study of a Buck-Boost circuit[J]. Journal of System Simulation, 2004, 16(1): 52-54.
[13] 薛禹胜, 朱少林, 彭志炜, 等. Buck-Boost 换流器中分叉现象的机理及预测[J]. 电力系统自动化, 2004, 28(3): 19-23.
XUE Yu-sheng, ZHU Shao-lin, PENG Zhi-wei, et al. The mechanism and prediction of bifurcations in Buck-Boost converter[J]. Automation of Electric Power Systems, 2004, 28(3): 19-23.
[14] 赵益波, 罗晓曙, 唐国宁, 等. 电流反馈型Buck-Boost变换器的非线性动力学研究[J]. 广西师范大学学报: 自然科学版, 2005, 23(2): 9-12.
ZHAO Yi-bo, LUO Xiao-shu, TANG Guo-ning, et al. Study of nonlinear dynamics behaviors based on current-programmed Buck-Boost converter[J]. Journal of Guangxi Normal University: Science and Technology, 2005, 23(2): 9-12.
[15] 徐德鸿. 电力电子系统建模及控制[M]. 北京: 机械工业出版社, 2007: 25-33.
XU De-hong. Control and modeling of power electrical system[M]. Beijing: Mechanical Industry Press, 2007: 25-33.
[16] 胡德文, 董国华. 混沌控制: 回顾与展望[J]. 国防科技大学学报, 2000, 22(1): 77-80.
HU De-wen, DONG Guo-hua. Chaos control: A review and prospect[J]. Journal of National University of Defense Technology, 2000, 22(1): 77-80.
(编辑 陈爱华)
收稿日期:2011-05-22;修回日期:2011-07-11
基金项目:国家自然科学基金创新研究群体基金资助项目(50721063);国家自然科学基金资助项目(51077131,50737004)
通信作者:袁雷(1985-),男,河南虞城人,博士研究生,从事电力电子技术及电气传动研究;电话:027-83443297;E-mail: yuanl886@yahoo.com.cn