J. Cent. South Univ. Technol. (2008) 15(s1): 256-260
DOI: 10.1007/s11771-008-358-3
Application of higher order spectrum in analysis of magneto-rheological damper control
LIU Xiao-mei(刘晓梅), HUANG Yi-jian(黄宜坚), CHEN Jun-jie(陈俊杰)
(College of Mechanical Engineering and Automation, Huaqiao University, Quanzhou 362021, China)
Abstract: Higher order spectral analysis can be used to identify nonlinearities in the complex dynamical systems. This proposal shows that the contributions of the bispectrum, trispectrum, reconstructed bispectrum and reconstructed power spectrum in terms of the system frequency response function and elementary physical properties of the MR damping system. Subsequent estimates of the HOS based on the output stochastic oscillating signals appear distinct variation. An experimental platform for MR vibrating semi-active control is built, proper simplifications are presented, an AR(10) model is established with colored noises from the output signals. Comparison between power spectrum from second order moment function and bispectrum, trispectrum are taken. The later gives an indication of the correlation between the phases of different frequency components. Since time series model is a parametric model, the reconstructed bispectrum and power spectrum are smooth. It is demonstrated that the higher order spectra are effectively for recognition and description of nonlinear systems.
Key words: MRF; vibrating control; time series; higher order spectrum; bispectrum; trispectrum
1 Introduction
Magneto-rheological fluid (MRF) is a smart soft-matter that can reversibly change from Newtonian fluid to viscoplaster with controllable yield strength in few milliseconds when it is exposed to a magnetic field. The technology of MRF is widely applicated in many fields, such as damper, actuator, finishing of silicon wafer, hydraulic and pneumatic system, sealing for its performance of high strength, lower viscosity, temperature stability, consuming fewer energy and insensitive to impurity. Damper and actuator are typical applications of MRF[1].
Nonlinearities are prevalent in many mechanical systems. The development of analytical models and the estimation of model parameters from observed output data are critical to understand the behavior of dynamical systems. Modeling and estimation become difficult, when systems exhibit nonlinear behavior. Nonlinearities exist in the oscillation of mechanical systems due to the material of magneto-rheological fluid and the geometric effects by the MR damper design.
For linear systems, the principle of superposition takes into account second-order relationships (power spectrum), which is the essence, and the system is only described by the amplitude but lacks the phase coupling information of time series. The superposition and the classical model approach may fail in providing a satisfactory description in a non-Gaussian process. For nonlinear systems, the analysis based on higher order cumulants or higher order spectra (HOS) will be proven to be a useful tool in modeling and describes the dynamic characteristics and signal processing[2].
2 Analysis of higher order spectrum
Higher order spectrum (HOS) is the extension and development of the conception of power spectrum. The power spectrum is the frequency domain representation of second-order relationship, higher order spectra are the multidimensional Fourier transforms of higher order cumulants, bi-spectrum and tri-spectrum are the staple applications nowadays. Higher order spectrum contains abundant information concerning the system and is superior to the power spectrum in the analysis and control of nonlinear systems.
1) Higher order spectrum can restrain the additive white noise because it is insensitive to the Gaussian noise.
2) The amplitude and the phase of the signals can be reconstructed using the higher order spectrum.
3) Higher order spectrum is a useful tool to detect the construction of nonlinear system.
2.1 Higher order spectrum
Higher order spectrum ordinarily defines through higher order cumulants[2]. On the assumption, time series x(k) have additive nth order cumulant  , then defining the (n-1)dimensional Fourier transform as the nth order spectrum of the time series x(k), it can be denoted as
, then defining the (n-1)dimensional Fourier transform as the nth order spectrum of the time series x(k), it can be denoted as

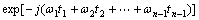 (1)
(1)
The field of definition of the higher order spectrum is |ωi|≤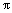 , i=1, 2, …, n-1, i.e. |ω1+ω2+…+ωn-1|≤
, i=1, 2, …, n-1, i.e. |ω1+ω2+…+ωn-1|≤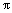 . Commonly, HOS is a complex number, and it can be also expressed as
. Commonly, HOS is a complex number, and it can be also expressed as
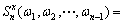
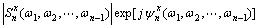 (2)
(2)
Specially, when n=2, it becomes power spectrum.
2.2 Bi-spectrum
As the abovementioned definition of higher order spectrum, the bispectrum is the case of n=3, it becomes second dimensional Fourier transformation of the three order cumulant, and is described as
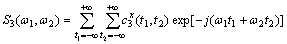 ,
,
ω1≤ , ω2≤
, ω2≤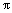 , |ω1+ω2|≤
, |ω1+ω2|≤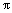 (3)
(3)
here 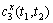 is the three order cumulant sequence of the time series x(k)[3-5].
is the three order cumulant sequence of the time series x(k)[3-5].
For white non-Gaussian process, it has
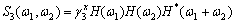 (4)
(4)
here 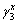 is the skewness.
is the skewness.
Power spectrum can be reconstructed from bispectrum through
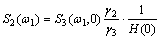 (5)
(5)
Bispectrum reflects the system skewing to the Gaussian process, provides the effects of different frequency coupling to the dynamic characteristics of the system.
2.3 Tri-spectrum
Trispetrum is the three dimensional Fourier transform of the fourth order cumulant, it can be written as
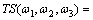
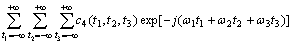 (6)
(6)
The trisprectrum of white non-Gaussian process can be expressed as
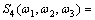
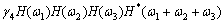 (7)
(7)
here  is the kurtosis.
is the kurtosis.
Trispectrum can inspect and quantificationally depict the cubical phase coupling of the process. Bispectrum can also be reconstructed from trispectrum through
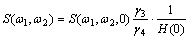 (8)
(8)
3 Results
The flow behavior of MRF can be modeled by the power law equation:
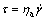 (9)
(9)
where τ is the shear stress, Pa;  is the shear rate, s-1; ηa is the apparent viscosity, Pa?s, which can be represented by:
is the shear rate, s-1; ηa is the apparent viscosity, Pa?s, which can be represented by:
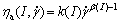 (10)
(10)
here I is electric current, A; k(I) is consistency; β(I) is a function of the electric current I [6-8].
The MR damping force can be controlled by changing the electric currents. The relationship between the fluid resistance fd and applied electric current can be expressed as
 (11)
(11)
where L is the length of the piston, m; Rpo and Rci are the radiuses of the piston and the inner radiuses of the cylinder, m; h is the gap between the piston and the cylinder, m; N is the turn number of the coil; u is the velocity of the piston, m/s[9-10].
3.1 AR model
Assuming that the non-Gaussian white noise a(t) which is contained in the output displacement signals is the input of the process, the AR model responding to an autoregressive process can be written as[3]
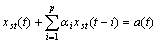 (12)
(12)
where p is the order of the AR model.
The zero mean colored non-Gaussian noise xst(t) which is carrying abundant information of MR damper dynamic characteristics is regarded as the output of the autoregressive process driven by a(t).
In this proposal, an AR(10) model is built.
3.2 Power spectrum
Power spectrum (shown in Fig.1) obtained from the AR(10) model describes the energy distribution with frequencies of the MR damper. The power spectrum which is sensitive to the Gaussian noise does not contain the phase information of the system.
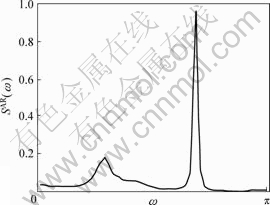
Fig.1 Power spectrum SAR(ω)
3.3 AR bispectrum
Fig.2 shows the AR bispectrum of the MR vibration platform when the applied electric current is 0.5 A. It indicates the effect on the system dynamic characteristics from the phase coupling of different input signals.
From Fig.2, it can be seen from following.
1) The variation in the bispectrum is more evident than that of the power spectrum because the bispectrum is much sensitive than the latter.
2) All of the valuable information is contained in the inner triangular domain, and the spectrum is sufficient for the description of the bispectrum characteristics.
3) In the abovementioned inner triangular domain, the peaks of bispectra occur, which indicates that the process is non-Gaussian and non-linear coupling exists in the system. The reason of this may be the power accumulator which deposits and complements MRF to the MR damper cylinder.
3.4 AR Trispectrum
The modulus of the trispectrum is a function of three frequency variables and so requires four- dimensional space to display it. Here, it attempts to display the magnitude of the entire trispectrum to give an overall picture of the trispectral information. Fig.3 depicts the magnitudes of the trispectrum for I=0, 1.0 and 2.0 A.
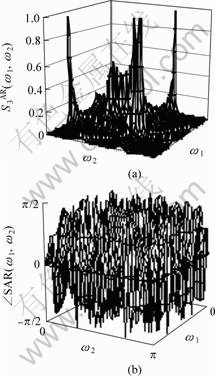
Fig.2 AR bispectrum(a) and phase angle(b)

Fig.3 Trispectrum TSAR: (a) Trispectrum for I=0 A; (b) Trispectrum for I=1.0 A; (c) Trispectrum for I=2.0 A; (d) Contours for I=2.0 A
3.5 Reconstruction of BS and power spectrum
The bispectrum BSAR(ω1, ω2) can be obtained from the slice of the trispectrum. In traditional manner, the reconstructed bispectrum of some slices of the trispectrum are displayed in Fig.4. Figs.4(a)-(c) show the slices TSAR(ω1, ω2, π), TSAR(ω1, 0.14π, ω3) and TSAR(0.24π, ω2, ω3).
Fig.5(a) shows the power spectrum TSAR(π, ω2, π) for differential electric currents, and Fig.5(b) shows the power spectrum TSAR(ω1, ω2, π) of I=2.0 A.
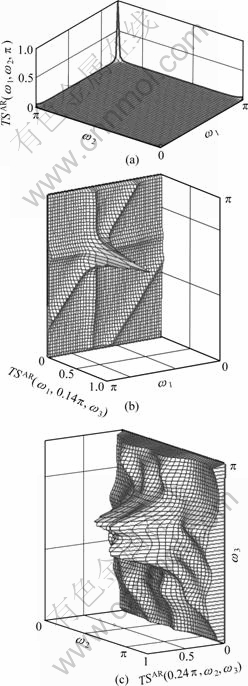
Fig.4 Reconstructed bispectra: (a) TSAR(ω1, ω2, π) of I=0 A; (b) TSAR(ω1, 0.14π, ω3) of I=1.0 A; (c) TSAR(0.24π, ω1, ω2) of I=2.0 A
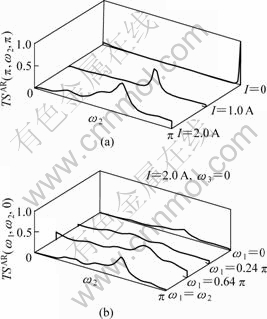
Fig.5 Reconstructions of power spectrum: (a) Differential electric currents; (b) I=2.0 A
The bispectrum and trispectrum can inhibit the Gaussian signals, but the power spectrum is sensitive to the Gaussian signal. The performance of the reconstructed spectrum BSAR(ω, 0) and TSAR(ω, 0, 0) are better than that obtained directly from second-order moment function.
4 Conclusions
1) When a zero mean and non-Gaussian white noise interferes with the magnetorheological damping device, the AR(10) model can be established to investigate the dynamic characteristics of MR system.
2) The bispectrum eliminates additive Gaussian noise and provides the information of phase coupling.
3) The largest magnitude of the trispectrum in this paper leaves the point (π, π, π) when controllable electric current increases.
4) The bispectrum can be reconstructed from the trispectrum, and power spectrum could be reconstructed from the bispectrum or trispectrum.
5) The higher order spectrum can dispose the non-Gaussian process effectively, depict the phase coupling of MR damping system and identify the non-linear characteristics by restraining the additive Gaussian noise automatically.
References
[1] JOLLY M R, BENDER J W, CARLSON J D. Properties and applications of commercial magnetorheological fluids[EB/OL]. http://www.mrfluid.com, 2006-03-27.
[2] SCHURTER K C, ROSCHKE P N. Fuzzy modeling of a magnetorheological damper using ANFIS[C]// The 9th IEEE International Conference on Meeting. FUZZ IEEE 2000, 2000: 122-127.
[3] YANG Shu-zi, WU Ya. Engineering applications of time series analysis[M]. Wuhan: Huazhong University of Science & Technology Press, 1994: 181-187. (in Chinese)
[4] LIU Fu-sheng, LUO Peng-fei. Statistic signal process[M]. Beijing: National University of Defense Technology Press, 1999: 225-230. (in Chinese)
[5] ZHANG Xian-da. Time series analysis[M]. Beijing: Tsinghua University Press, 1999. (in Chinese)
[6] WANG D H, LIAO W H. Neural network modeling and controllers for magnetorheological fluid dampers[C]// IEEE International Fuzzy System Conference. 2001: 1323-1326.
[7] GUO D L, HU H Y, YI J Q. Neutral Network control for a semi-active vehicle suspension with a magnetorheological damper[J]. Journal of Vibration and Control, 2004, 10: 461-471.
[8] COLLIS W B, WHITE P R, HAMMOND J K. Higher-order spectra: The bispectrum and trispectrum[J]. Mechanical System and Signal Processing, 1998, 12(3): 375-395.
[9] YANG G. Q. Large-scale magnetorheokogical fluid damper for vibration mitigation: Modeling, testing and control[M]. Indiana, USA: University of Notre Dame, 2001.
[10] XIA Pin-qi. An inverse model of MR damper using optimal neural network and system identification[J]. Journal of Sound and Vibration, 2003, 266(5): 1009-1023.
(Edited by LI Yan-hong)
Foundation item: Project(A0610020) supported by the Natural Science of Fujian Province of China
Received date: 2008-06-25; Accepted date: 2008-08-05
Corresponding author: LIU Xiao-mei, PhD; Tel: +86-592-2188981; E-mail: liuxm@hqu.edu.cn