J. Cent. South Univ. Technol. (2007)04-0595-05

DOI: 10.1007/s11771-007-0114 -0

Optimization methods of cutting depth in mining Co-rich crusts

QIN Xuan-yun(秦宣云)¹, GUAN Ji-hong(管继红)¹, REN Bo(任  波)¹, BU Ying-yong(卜英勇)²

(1. School of Mathematics and Computing Science, Central South University, Changsha 410083, China;

2. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083,China)

________________________________________________________________________________________

Abstract: For optimizing the cutting depth of spiral drum type cutting head, the relations among collecting ratio, interfusing ratio of mullock and cutting depth of the mining cobalt-rich crusts in ocean were discussed. Furthermore, the multi-extremum problem about cutting depth was analyzed in mining at a certain interfusing ratio of mullock. Through introducing genetic algorithm (GA), the cutting depth-control problem when the collecting ratio is maximized by controlling the interfusing ratio of mullock was solved with global-optimization-search algorithms. Then optimization theory for cutting depth in mining cobalt-rich crusts by GA, and computer programming were given to realize the algorithm. The computation result of actual data proves the validity of this method.

Key words: Co-rich crust; collecting ratio; interfusing ratio of mullock; gene algorithm

________________________________________________________________________________________

1 Introduction

Because of the huge economic value and important tactic signification, a new competition for the contesting deep-sea mineral resources has been formed. Lots of researchers^[1-6] have studied the cause of formation about Co-rich crusts, and distribution of major deep-sea ore resources, and its future development. Accordingly, the research of mining deep seabed Co-rich crust is a hot spot of international oceanology^[7-9] . These researchers provided effective methods for design of mining head. And they indicated especially that parameters of all models rely on cutting depth in crushing process. But the research on optimizing cutting depth is fewer. The cutting depth is directly related to the efficiency of mining deep sea Co-rich crusts. Because of the complexity of tiny terrain in mining process, QIN et al^[10] gave a method of calculating the fractional dimension and proposed the rebuilding theory and calculation method. Based on these, the relations among collecting ratio, interfusing ratio of mullock and cutting depth were discussed in this paper. Furthermore, the problem of the multi-extremum about cutting depth was analyzed. Then optimization theory for cutting depth in mining cobalt-rich crusts by GA, and computer programming were given to realize the algorithm.

2 Relations among collecting ratio, inter- fusing ratio of mullock and cutting depth

In certain area, the depth of crusts can be considered

as a fixed value and the altitude data of the tiny terrain surface of the collecting area is available. Based on these, optimization of cutting depth was studied as follows.

2.1 Definitions of collecting ratio and interfusing ratio of mullock

The collecting ratio and the interfusing ratio of mullock are two important targets that can be used to measure the efficiency of mining. The representation of collecting ratio (q) is

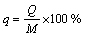              (1)

where  Q is the quantity of useful ore that has been picked up, M is the total quantity of useful ore contained at the gather-place. The representation of the interfusing ratio mullock(r) is

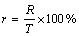            (2)

where  T is the quantity of gathered ore, R is the quantity of waste ore mixed in the gathered ore.

Considering the distribution and character of Co-rich crusts in ocean (such as crust inside with little mullock), all kinds of metals included in Co-rich crusts are regarded as useful ore; moreover, thinking the feasibility of research, each variable was measured by calculating its corresponding volume (V) which is derived by the dynamic effect model(DEM) data of tiny terrain when calculating the optimal cutting depth. Therefore, the collecting ratio (q) and the interfusing ratio of mullock (r) can be simplified as

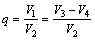              (3)

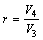                  (4)

where  V₁ is the volume of cobalt crusts(useful ore) gathered, V₂ is the total volume of cobalt crusts of the gather-place, V₃ is the total volume of gathered ore, V₄ is the volume of waste ore mixed in the gathered ore.

2.2 Determination of relations among collecting ratio, interfusing ratio of mullock and cutting depth

The main purpose is to improve the collecting ratio by controlling the cutting depth when the mullock is fixed. Because the total volume of cobalt crusts contained in the gather-place is a fixed value, and the distribution of Co-rich crusts exposed to seabed is continuous, when not all of the crusts are picked up, as the increase of the cutting depth, the amount of gathered cobalt crusts increases accordingly. In terms of the complexity of tiny terrain and the representation of collecting ratio, we can know that the relation between the cutting depth and the collecting ratio is not analytic; but it is valid that the collecting ratio increases as raising the cutting depth. Of course, when the cutting depth reaches a certain value, all of the cobalt crusts are picked up, and the collecting ratio reaches 100%. In this situation, the interfusing ratio of mullock is usually quite large, which maybe surpasses the acceptable interfusing ratio of mullock. Therefore, we should build a model to search for the optimal cutting depth with the largest collecting ratio, while the interfusing ratio of mullock is fixed. In fact, according to Eqn.(4), we know that V₃ and V₄ are all increased when raising the cutting depth. So we cannot give an analytical function to indicate the relation between the interfusing ratio of mullock and the cutting depth. In order to make the question clear, two special cases will be given as follows.

Case 1: In the simplified situation as shown in Fig.1, the following assertions are valid:

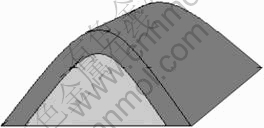
Fig.1 Case for only one relatively high protuberance with relatively flat and short surface around it

1) When the cutting depth is smaller than the thickness of crusts, the mullock is identically vanishing, since all of the gathered ores are Co-rich crusts which can be regarded as useful ore;

2) When the cutting depth is larger than the thickness of crusts, when raising the cutting depth, the interfusing ratio of mullock is increased necessarily. In fact, we can simplify this situation, as Fig.2 showing approximately. Given h is the thickness of waste ore, t is the thickness of crusts that is fixed, α is the angle between the vertical plane and the crust plane, the cutting depth is h+t, and the interfusing ratio of mullock(r) is given by

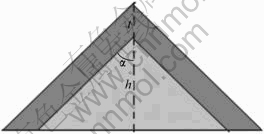
Fig.2 Simplification of case for only one relatively high protuberance with relatively flat and short surface around it

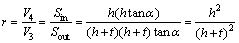  (5)

Obtaining its derivation:

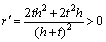          (6)

so r is a increasing function of h.

Case 2: As shown in Fig.3, if only considering the highest wave crest of cobalt crusts the situation can be treated as case 1, but the crusts also contain flat part. In order to explain the question explicitly, we assume that the cobalt crusts only contain one wave crest with plenty of flat crusts around it. As shown in Fig.4, when the cutting depth is between h₀ and h₁, the situation can also be treated as case 1; when the cutting depth is between h₁ and h₂, raising h, r is decreased accordingly, because V₃ becomes much larger than V₄ as the cutting depth increases.

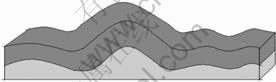
Fig.3 Case for only one relatively high protuberance with relatively flat and long surface around it

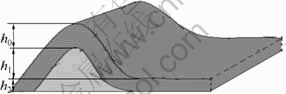
Fig.4 Simplification of case for only one relatively high protuberance with relatively flat and long surface around it

According to the analysis mentioned above, case 1 and case 2 are all possible because of the complexity of ocean terrain. Therefore, the transform relativity of r and the cutting depth is uncertain. Because q is increased as the cutting depth increases, we can increase q by increasing the cutting depth. However, the interfusing ratio of mullock cannot be neglected in actual mining, because the high interfusing ratio of mullock influences the mining efficiency seriously, the method in common use is to improve the collecting ratio as much as possible, given the acceptable maximum of interfusing ratio of mullock. In other words, we should search for the maximum cutting depth that satisfies the control- condition of the interfusing ratio of mullock. But the relation between interfusing ratio of mullock and cutting depth is uncertain. For a given interfusing ratio of mullock, there are possible multitudes of cutting depth values corresponding to it. Therefore, the main problem actually is a complicated multi-extremum problem which most of the traditional search-methods are not suitable to deal with,while genetic algorithm is just suited to this problem^[11-14].

3 Genetic algorithm of optimal cutting depth in mining deep-sea-cobalt-rich crusts

By analyzing the geometrical character of tiny terrain and the relation between the collecting ratio and the interfusing ratio of mullock in mining, we know that the optimized process of the cutting depth needs to deal with the multi-extremum problem firstly. For this reason, GA will be used to optimize the cutting depth; the following content gives the specific realizing process.

First of all, the selected interval of the cutting depth should be determined. Usually the lower limit of the interval is the thickness of cobalt-rich crusts, and the upper limit is the thickness of cobalt-rich crusts adding the maximum of DEM subtracting the minimum of DEM. In advance, the number of the cutting depth values (POPSIZE means the initial community scale) selected from the selected interval should be given, and the fitness of the cutting depth can be calculated; then the optimal cutting depth is obtained. At the same time, the gene-hybridized operation is conducted among some of the cutting depth values in a certain proportion (swapping the bits of the binary coding corresponding with the cutting depth), so the new generation synthesizes the excellent genes from different paternal members. In addition, implementing the mutating operation to tiny minority of the cutting depth values, the new members can join the colony, and the whole process of converging to the local optimal value is not too rapid. The operations mentioned above (such as reproducing, swapping and mutating) produce a new generation, to which the same operations will be implemented. The circulating process cannot be finished until the entire optimized process satisfies the end-conditions. In the calculating process, the following questions will be mentioned.

1) Coding for the cutting depth. Using the binary bits (0/1) to code, firstly the feasible solutions should be expanded to certain multiple to become a corresponding integers (in other words, the feasible solutions should divide the precision of calculating ε), which are mapped to a group of feasible solutions beginning with zero. Next, the length of the binary coding L should be settled,

since^[14] 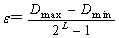, L is given by

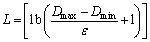       (7)

where [ ] is a function of rounding to integral part; D_max is the maximum of the DEM data; D_min is the minimum of the DEM data.

2) Constructing the fitness function. Usually the fitness function is defined according to the purpose of the optimized problem, for this reason, the fitness function is required to satisfy the conditions that the maximum of acceptable interfusing ratio of mullock is reached; and the cutting depth value is the largest one. Therefore, the fitness function f(h) is defined as follows:

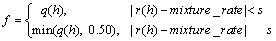(8)

where  q(h) is the function of the collecting ratio, mixture ­­_­­­-­^­rate is the maximum of acceptable interfusing ratio of mullock, s is a given constant that locates at the interval 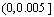, usually the collecting ratio is larger than 50%.

3) Reproducing. Reproducing reflects the principle that only the one who adapts to the environment can survive. Implementing the reproduce operation only according to the fitness can keep the excellent individuals, but it is not sure that the better individuals can be discovered, so in the implementation of the algorithm, the objects that will be reproduced are selected by the method of random sampling.

4) Swapping. This operation is used to swap two individuals selected from the colony randomly. The specific approach of this problem is: producing a random number i that derives from the integral set{1, 2, …, L-1} by the uniform-distribution; swapping the relevant bits of the binary coding of two cutting depth values from i+1 to L; obtaining two new binary codings.

5) Mutating. The purpose of this operation is to replenish the colony with new individuals, so that the process of converging to the local optimal value is not too rapid. The individuals to which the mutating operation will be implemented are selected by the character-determined method. In programming process, the probability constant of mutating (PMUTATION: usually the constant is very small in GA) should be given beforehand, then for each character, a random number satisfied the uniform-distribution is obtained from [0, 1] corresponding to it, if this random number is smaller than PMUTATION, the mutating operation will be implemented.

6) The criterion of ending the operations. In connection with the specific problem on which we research, the approach in common use is to control the maximum of iteration-times, if the times of iteration reaches the maximum, the operations will be ended. Finally, the optimized solution is the best cutting depth in the whole process.

4 Programming realization of GA of optimized cutting depth and examples

4.1 Programming realization of GA of optimized cutting depth

Using the Visual C++ develop-platform, the class of optimized cutting depth is defined to realize the application of GA, the structures and classes are defined as follows:

1) Structure of the cutting depth

struct genotype

{int *gene;//the address of the binary coding of cutting depth

 double fitness;   //the fitness of cutting depth

 double rfitness;  //the relative fitness

 double cfitness;  //the accumulative fitness

 double value;    //the cutting depth value};

2) Object class of GA

class GA

{ public:

  GA();           //construct function

  ~GA();          //destruct function

  double pro();     //optimize the cutting depth values

……

void SetGA       //the initial function

(double height,   //the thickness of cobalt crusts

double rate,  //the maximum of acceptable interfusing ratio of mullock

struct genotype newpopulation[51],//the new generation colony

struct genotype population[51],//the present generation colony

int cur_best,     //the best individual

int generation  //the number of generation,means the iteration-times);

void mutate();        //the mutate-function

void swap(int*,int*);  //swap the bits of two binary coding

void Xover(int,int);   //select the bits which will be swapped

void crossover();     //select the individuals which will be swapped

void select();      //in turn select the individuals which need to be reproduced

void elitist();     //getting the best by sifting

void keep_the_best();  //keep the best

void evaluate();      //the fitness function

double randval(double,double); //produce the cutting depth values randomly};

The following content is to annotate some of the functions in the above-mentioned class.

1) The initial value of cutting depth is produced randomly by compiling the function: double randval(double, double), while the cutting depth is acceptable, and the fitness is given as zero. Then the DEM data is read from the DEM files(format as:*.txt).

2) Compiling the fitness function:void evaluate( ). Its purpose is to get the value of h when f reaches its maximum, and r is close to the maximum of acceptable interfusing ratio of mullock.

3) Compiling the sift-function: void elitist( ).The best member of the present generation is saved as the last one of the sequence. If the best member of the new generation is worse than one of the present generation, the latter will replace the worst member of the new generation; if not, the former will be reproduced.

4) Compiling the select-function: void select( ). It is used to cooperate with the sift-function to make sure the best will be selected.

5) Compiling the hybridize-function: void cross- over( ). void Xover(int, int) is used to execute the hybrid of two selected individuals from the paternal generation, and void swap(int*,int*) is used to swap the genes.

6) Compiling the mutate-function: void mutate( ). The mutate increment which has been selected is replaced by a random number in the range of the variable.

7) The use of the function: double pro( ) is to transfer the above-mentioned functions, n order to get the optimal result.

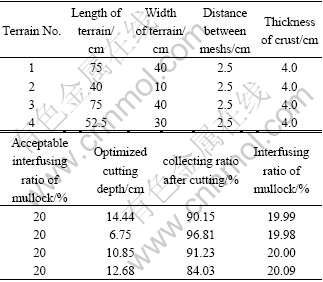
4.2 Examples

For several groups of altitude data of tiny terrain in trials, setting the acceptable interfusing ratio of mullock to be 20%, the above method is used to perform the calculation of the optimized cutting depth. The result is shown in Table 1.

As shown in Table 1, the results of cutting depth calculated with the method of optimized theory are satisfied. Therefore, it could be used in the optimized control of cutting depth in mining co-rich crusts in deep sea.

Table 1 Calculation results of cutting depth and interfusing ratio of mullock and collecting ratio for several groups of tiny terrains with optimized theory of cutting depth

5 conclusions

1) Based on the rebuilding theory system and calculation method of tiny terrain on mining process, the relations among collecting ratio, interfusing ratio of mullock and cutting depth were studied. Furthermore, the problem of the multi-extremum about cutting depth was analyzed.

2) Optimization theory for cutting depth in mining cobalt-rich crusts by GA was built.

3) Computer programming was given to realize the algorithm for cutting depth in mining cobalt-rich crusts by GA.

[1] HE Gao-wen, LIANG Dong-hong, SONG Cheng-bing, et al. Determining the distribution boundary of cobalt-rich crusts of guyot by synchronous application of sub-bottom profiling and deep-Sea video recording[J]. Earth Science—Journal of China University of Geosciences, 2005, 30 (4): 509-512.(in Chinese)

[2] SHEN Yun-jun, ZHONG Xiang, HE Ze-quan. Present status of investigation and development of ocean cobalt crust resources[J]. Mining and Metallurgical Engineering, 1999, 19(2): 11-13. (in Chinese)

[3] MOON Jai-woon, et al. Current state and future prospect of Korean activities on the seafloor sulfides and cobalt-rich crusts[C]// International Symposium on New Deep Seabed Mineral Resources Development Policy. Ansan, Korea, 2004.

[4] YAMAZAKI T, SHARMA R. Morphological features of Co-rich mangance deposites and their relation to seabed slopes[J]. Marine Georesources & Geotechonology, 2000, 18(1): 43-76.

[5] GLASBY G P. Deep seabed mining: Past failures and future prospects[J]. Marine Georesources and Geotechnology, 2002, 20(2): 161-176.

[6] WU Guang-hai, MA Wei-lin, LIU Jie-hong, et al. A method for finding the ore block of Co-rich crusts on seamounts[J]. Journal of Maring Sciences, 2005 23(4): 15-19. (in Chinese)

[7] LIU Yong. Theoretic and experimental research of method for applying twist-roller to cut and collect deep-sea cobalt crust[D]. Changsha: Shool of Mechanical and Electrical Engineering,Central South University, 2002.(in Chinese)

[8] LUO Chun-lei, HU Jun-ping, LIU Wei. Device and methods of mining cobalt crust[J]. Journal of Central South University of Technology: Natural Science, 2002, 33 (6): 617-620. (in Chinese)

[9] XIA Yi-ming, BU Ying-yong, TANG Pu-hua, et al. Modeling and simulation of crushing process of spiral ming head[J]. Journal of Central South University of Technology, 2006,13(2): 171-174.

[10] QIN Xuan-yun, BU Ying-yong, XIA Yi-ming et al. The reconstructing of the tiny terrain based on fractal theory[J]. Journal of National University of Defense Technology, 2003, 25(5): 44-47. (in Chinese)

[11] REN Ping. Genetic algorithm(an overview)[J]. Journal of Engineering Mathematics, 1999, 16(1): 18-19. (in Chinese)

[12] WU Guang-hao, WEN Yi, LE Mei-feng. Genetic algorithm and its application in structure optimization[J]. Chinese Journal of Applied Mechanics, 1996,13(2): 93-98. (in Chinese)

[13] ZHANG Xiao-ji, DAI Guan-zhong, XU Nai-ping. Genetic algorithms—A new optimization and search algorithms[J]. Control Theory and Applications, 1995, 12(3): 265-273. (in Chinese)

[14] YUN Qing-xia, HUANG Guang-qiu, WANG Zhan-quan. Genetic Algorithm and Genetic Programming[M]. Beijing: Metallurgical Industry Press, 1997: 4(in Chinese)

_____________________________

Foundation item: Project（50474052）supported by the National Natural Science Foundation of China; Project(2005) supported by the Youthful Teacher Skeleton Foundation of Hunan Province, China; Project supported by the Postdoctoral Foundation of China

Received date: 2007-02-20; Accepted date: 2007-04-23

Corresponding author: QIN Xuan-yun, PhD, Associate professor; Tel: +86-731-8710774; E-mail: admath@mail.csu.edu.cn

(Edited by YANG Hua)