文章编号：1004-0609(2009)02-0235-06

Al6061/20SiCw板材的超塑成形极限与空洞行为

赵祖德¹，窦小丽²，王艳彬¹，舒大禹¹，胡传凯¹，童国权²

(1. 中国兵器工业第五九研究所，重庆 400039；

2. 南京航空航天大学 机电学院，南京210016)

摘  要：对Al6061/20SiC_w板材在单向拉伸和等双向拉伸应力状态下的孔洞行为进行研究。利用长轴与短轴比分别为1:1和2:1的胀形模具，在恒定应力2 MPa，温度873 K的条件下，研究Al6061/20SiC_w板材的成形极限。基于MARCHINIAK-KUCAYNSKI(M-K)模型和塑性损伤模型，提出一种用于预测Al6061/20SiC_w板材在双向拉伸应力状态下的极限应变的分析模型。结果表明：在相似的等效应变速率下，等双向拉伸应力产生的孔洞数量稍多于单向拉伸应力产生的孔洞数量；对于无初始几何缺陷的Al6061/20SiC_w板材，分析模型能较为准确地预测复合材料在双向拉伸条件下的极限应变。

关键词：铝基复合材料；超塑性；孔洞；成形性

中图分类号：TG 316           文献标识码：A

Forming limits and cavitation behaviors of superplastic Al6061/20SiCw sheet

ZHAO Zu-de¹, DOU Xiao-li², WANG Yan-bin¹, SHU Da-yu¹, HU Chuan-kai¹, TONG Guo-quan²

 (1. No. 59 Research Institute of China Ordnance Industry, Chongqing 400039, China;

2. School of Electromechanical Engineering, Nanjing University of Aeronautics and Astronautics,

Nanjing 210016, China)

Abstract: The cavitation behaviors of Al6061/20SiC_w sheet under uniaxial and equibiaxial tension stress states were investigated. The forming limits of Al6061/20SiC_w sheet under biaxial tension using dies with aspect ratios of 1:1 and 2:1 at constant applied stress of 2 MPa and at 873 K were also investigated. An analytic model based on the MARCHINIAK- KUCAYNSKI(M-K) and plastic damage models was proposed to predict the limiting strains of Al6061/20SiC_w sheet under biaxial tension stress state. The results show that at a similar effective strain rate, the amount of cavities obtained under equibiaxial tension states is slightly greater than that under uniaxial tension states. Under the condition of Al6061/20SiC_w sheet without original geometric deficiency, the prediction of the analytic mode is in agreement with the limiting strains under biaxial tension state.

Key words: aluminum-based composite; superplasticity; cavitation; formability

铝基复合材料(Al-MMCs)具有比强度高、比刚度高和热膨胀系数低等一系列优良的综合物理机械性能，在车辆、兵器、航空航天、电子等领域有重要的应用前景。但是，由于增强体的加入，使得铝基复合材料的室温塑性低，冷成形性能差，从而给二次加工带来很大的困难。超塑成形技术的出现为推动铝基复合材料的工业应用，特别是为铝基复合材料板材在汽车车体上的应用提供了一条途径。采用超塑成形铝基复合材料具有成形压力低、材料可进行大变形和实现近净形成形等优点，因此，研究铝基复合材料板材的超塑成形就显得很重要^[1]。

TEE等^[2]研究表明：Al-MMCs具有高应变速率的超塑性效应，最佳应变速率为10^?2 s^?1。这比经典超塑成形的最佳应变速率提高约2个数量级，使得成形效率不再是Al-MMCs超塑性的障碍。目前，Al-MMCs 超塑研究的主要方向为：变形特性和变形机理^[3?8]；变形对微观组织，尤其是对孔洞的影响^[9?10]。在单向拉伸、等双向拉伸和平面应变条件下，YAMAMOTO   等^[11]研究了Al-10Si-Mg/SiC_p的成形性，得出成形极限图。研究表明：Al-10Si-Mg/SiC_p的最小成形极限出现在等双向拉伸区域，最大的成形极限出现在单向拉伸区域。这与传统的薄板金属成形性不同，薄板金属成形的最小成形极限出现在平面应变区域。根据MARCHINIAK- KUCAYNSKI (M-K)模型^[12]，运用损伤力学原理，TONG等^[13]建立了等双向拉伸下的超塑成形性分析模型，其极限应变预测值与Al-6Mg-0.3Sc合金超塑性实验结果吻合良好。极限应变值是板材超塑成形工艺设计的基础。

在实际工程中，板材成形过程多是在双向拉伸应力状态下进行的，而等双向拉伸应力状态只是板料成形中的特例。因此，判断等双向拉伸应力状态下的超塑成形性分析模型能否较为准确地预测铝基复合材料板材在双向拉伸条件下的极限应变，对实际工程中铝基复合材料板材超塑成形很重要。

在此，本文作者首先进行超塑单向拉伸和自由胀形，定量分析Al-MMCs 超塑成形变形量与孔洞体积分数的关系；然后，基于M-K模型和塑性损伤模型，提出一种用于预测Al6061/20SiC_w板材在双向拉伸应力状态下极限应变的分析模型，并对分析模型预测的Al6061/20SiC_w板材在双向拉伸条件下的极限应变进行检验。

1  实验

本研究采用β-SiC_w作为增强相，其直径为0.3~1.3 ?m，长为5~80 mm。采用Al 6061 粉末作为基体，粉末的粒度大约为25 ?m，其合金成分(体积分数，%)为：Al-1.01 Mg-1.07Si-0.35Cu-0.25Fe-0.05Mn-0.12Cr。复合材料采用粉末冶金法制备。将Al 6061 合金粉末和体积分数为20%的β-SiC_w共同在VH-500混粉机中机械混合12 h后进行冷压实，经除气处理后真空热压成复合材料锭；在773 K下以10?1的挤压比热挤压成板坯，然后在793 K下进行热轧。每道热轧的变形量为10%，每道热轧之间退火保温10 min以消除残余应力防止开裂。热轧的总变形量为80%，板材的最终厚度为2 mm。

在空气氛围中，使用配有三段式对开型电加热炉的岛津DCS2000 型拉伸试验机，进行单向拉伸试验，沿轧制方向取样，拉伸试样标距为7.5 mm×6 mm×  1 mm(长×宽×厚)。在拉伸实验过程中，严格控制目标温度，确保炉膛温度变化为±1 K。在自行研制的计算机控制的胀形试验机上进行超塑成形。胀形椭圆凹模的长轴为40 mm，长轴与短轴比分别为1?1和2?1，相应的双向拉伸应力比(β = σ₂/σ₁)分别为1.000 0和0.666 7。在胀形过程中，保持恒定的等效应力为2.0 MPa(相应的等效应变速率为0.15 s^?1)。将试样拉伸、胀形至预定的变形量后，中断实验，切割样品，每个样品均用排水法测定其相对密度，然后在装有自动图像分析软件的Leica Q500光学显微镜下观察孔洞形貌并进行孔洞体积分数自动图像分析。在自动图像分析时，每个样品观测10个视场，取其平均值，保证相对密度的测定结果和自动图像分析值之间的误差不大于10%。

2  结果与讨论

2.1  单向拉伸和等双向拉伸应力状态下的孔洞行为

图1所示为Al6061/20SiC_w超塑成形至破裂的试样照片。图1所示的圆形凹模和长轴与短轴比为2?1的椭圆凹模，其顶部厚向真应变分别为?2.19和?1.83。图2所示为Al6061/20SiC_w超塑单向拉伸和等双向拉伸下真应变与孔洞体积分数的关系。可见，在所有实验条件下，孔洞体积分数随应变量增大而增加。为方便比较， 图2还示出了传统超塑合金Al7475单向拉伸的孔洞行为。图2的实验数据点可以用方程φ_V=φ_V0exp(ηε)描述，φ_V0和φ_V分别是初始孔洞体积分数和一定应变下的孔洞体积分数，η为孔洞长大速率系数。结果表明：在Al6061/20SiC_w超塑变形过程中，孔洞长大取决于其附近材料的塑性变形^[14]。表1所列为某些超塑Al-MMCs和铝合金的φ_V0和η值。可见：Al6061/20SiC_w和其它超塑复合材料的η值相近，但小于传统超塑合金Al7475的η值。此外，本研究的φ_V0值高于已报道结果，这可能是自动图像分析结果往往偏高产生的。

图1  Al6061/20SiC_W超塑成形试样照片

Fig.1  Photos of superplastic formed Al6061/20SiC_w diaphragms with different die aspect ratios (T =873 K, σ=2 MPa): (a) 1?1; (b) 2?1

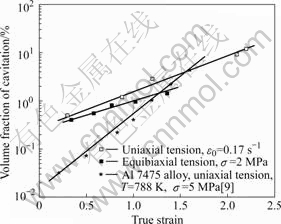
图2  孔洞体积分数与真应变的关系

Fig.2  Plots of φ_V with ε for Al6061/20SiC_w at 873 K

表1  部分超塑Al-MMCs和铝合金的φ_V0和η值

Table 1  φ_V0 and η for some superplastic Al-MMCs and aluminum alloys

由图2和表1可知，在相同应变下，等双向拉伸试样内部的孔洞分数略大于单向拉伸试样的孔洞分数，但两者的η值无明显差别。目前，应力状态对η值的影响尚未明确。MAHONEY等^[15]认为：应力状态(单向拉伸、等双向拉伸和平面应变)对Al7475合金的孔洞行为没有影响。由于超塑材料差异及其制备工艺不同，在讨论应力状态对孔洞行为影响时，应考虑显微组织特征(如基体晶粒尺寸、强化相及孔洞间隔等)因素。

为考察孔洞形貌，进行显微组织观测。图3(a)所示为以初始应变速率0.17 s^?1单向拉伸至应变等于0.33时的孔洞形貌，图3(b)和(c)分别为在等双向应力拉伸(σ=2 MPa)条件下，厚向真应变为?0.29和?2.19时的孔洞形貌。孔洞形貌观测表明：孔洞在强化相和基体的界面优先成核、长大；大变形试样内部孔洞长大到一定程度发生孔洞聚集，从而形成直径为10 mm左右的孔洞；应力状态对孔洞分布无明显影响。

图3  Al6061/20SiC_W孔洞形貌

Fig.3  Cavity morphologies of Al6061/20SiC_W deformed to  ε=0.33 (a) at 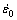= 0.17 s^?1 under uniaxial tension (tensile axis-horizontal), ε_t =?0.29 (b) and  ε_t =?2.19 (c) at σ=2 MPa under equibiaxial tension (sheet thickness-vertical)

2.2  预测的极限应变与实验结果的比较

当模腔长轴与短轴比分别为1?1和2?1时，Al6061/ 20SiC_w超塑胀形至破裂(见图1)，破裂区附近的厚向应变分别为?2.19 和?1.83。为预测极限应变，建立一种基于M-K模型和塑性损坏模型的分析模型。

依照M-K模型的分析，作如下假设。

(1) 铝基复合材料内部存在初始几何缺陷即初始沟槽，且与主应力方向平行，如图4所示。将初始几何不均匀性系数f₀定义为f₀=t_B0/t_A0，其中t_B0和t_A0分别表示沟槽内、外材料的初始厚度。

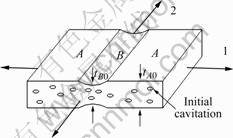
图4  沟槽模型

Fig.4  Geometry of groove (1, 2 represent x, y axial directions)

(2) 铝基复合材料内部存在初始物理损伤，并认为它是影响铝基复合材料超塑成形性的主要因素，则有材料等效初始不均匀因子F₀：

在最佳超塑变形温度下，假设铝基复合材料各向同性，满足Backofen本构方程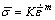，并遵循von Mises屈服准则，考虑体积不变定律，双向拉伸下的等效应

力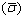和等效应变增量分别为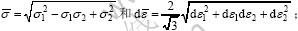与von Mises屈服准

则相结合的流动准则为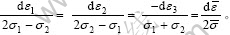区域A和B的平衡条件为：

在本研究中，假设复合材料在等双向拉伸和双向拉伸时，其η值相同，取η = 1.6，式(2)可写为

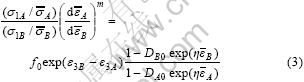
给定α、m、η、D_B0、D_A0和f₀，就可以用Runge-Kutta法对方程(8)求解。当x和t增加时，y值将降低；当y=0时，x值就是极限应变。

在本研究中，几何不均匀性系数f₀的变化范围为1~0.99。假定材料在沟槽内外的初始损伤不一致，D_B0/D_A0的变化范围为1.0~2.0。图5所示为Al6061/ 20SiC_w在不同f₀，等双向拉伸β=1.000 0和双向拉伸β=0.666 7下的理论成形极限。由图5可知，理论极限应变随着f₀增大而增大。若板材无初始几何缺陷，即f₀=1，本模型能够成功地预测Al6061/20SiC_w板材在双向拉伸条件下的极限应变。此外，当应力状态由等双

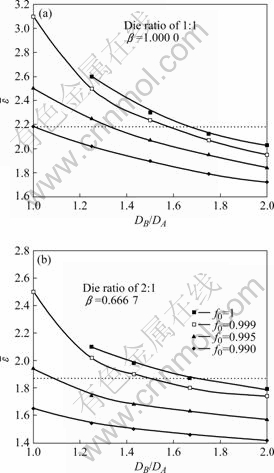
图5  f₀ 对成形极限的影响(虚线为实验结果)

Fig.5  Predicted formability for different f₀ (dashed line— experimental results): (a) Die ratio of 1?1, β=1.000 0; (b) Die ratio of 2?1, β=0.666 7

向拉伸β=1.000 0变化到双向拉伸β=0.666 7时，板料的成形性显著下降。当f₀=1时，D_B0/D_A0等于1.65±0.05，理论极限应变和实验结果吻合良好。对Al6061/20SiC_w复合材料，因为空洞分布不均匀，D_B0/D_A0的取值范围为1.6~1.7是合理的。值得注意的是，在TAI^[16]的损伤模型中，D_B0/D_A0值可从1变到5，他认为该范围可以接受。如果假设板料存在微小的初始几何不均匀性，要使理论极限应变和实验结果相吻合，可以减小D_B0和D_A0之间的差值。实际上，对真实的Al6061/20SiC_w复合材料，f₀从0.995变化到0.999都可以认为是合理的取值范围。当f₀为0.995时，为了与实验数据一致，D_B0/D_A0值可取1.32和1.07。

3  结论

1) Al6061/20SiC_w板材超塑变形，孔洞首先在晶须/基体界面形核，孔洞长大受其附近材料的塑性变形控制。单向拉伸和等双向拉伸，Al6061/20SiC_w板材的孔洞行为没有明显的差异。

2) M-K模型和塑性损伤模型预测的成形极限随着f₀增大而增大，并随D_B0/D_A0增大而减小。假定材料不存在初始几何缺陷，当D_B0/D_A0为1.65±0.05时，理论极限应变与等双向拉伸和双向拉伸(应力比β=0.666 7)的实验数据吻合良好。对于铝基复合材料，因为空洞分布不均匀，D_B0/D_A0取值范围为1.6~1.7是合理的。超塑成形性分析模型在板料无初始几何缺陷的情况下，能较为准确地预测双向拉伸应力状态下的极限应变。

REFERENCES

[1] TONG G Q, CHAN K C. Comparative study of a high-strain-rate superplastic Al-4.4Cu-1.5Mg/21SiC_w sheet under uniaxial and equibiaxial tension[J]. Mater Sci Eng A, 2003, A325: 79?86.

[2] TEE K L, LU L, LAI M O. Improvement in mechanical properties of in-situ Al-TiB₂ composite by incorporation of carbon[J]. Mater Sci Eng A, 2003, A351: 227?231.

[3] LI A B, GENG L. Simulation of the large compressive deformation of metal matrix composites with misaligned whiskers[J]. Mater Sci Eng A, 2003, 358: 324?333.

[4] YAN X Q, LIU Y, FU M F. Model of nonlocal lubrication and approximate solution method in the cold extrusion[J]. Journal of Plasticity Engineering, 2004, 11(5): 54?56.

[5] IMAI T, MAO J F, DONG S L. High strain rate superplasticity of TiC particulate reinforced 2014 aluminum alloy composites[J]. Mater Sci Eng A, 2004, 364: 281?286.

[6] HAN L H, NIU J T, HU H. Study on high strain rate superplasticity of a 6061Al alloy composite reinforced with 30vol.% AlN particulate[J]. J Mater Eng Perform, 2004, 13(2): 200?207.

[7] XU X J, WANG W, CAI L. Superplasticity of a SiC particulate-reinforced 6A02Al matrix composite[J]. Rare Metals, 2004, 23(1): 84?87.

[8] MA A, NISHIDA Y. Superplasticity of fine-grained 20vol.%SiC whiskers reinforced 2024 aluminum alloy produced by ECAP with a rotary die[J]. Mater Sci Forum, 2007, 539(7): 2934?2939.

[9] IWASAKI H, TAKEUCHI M, MORI T, MABUCHI M, HIGASHI K. A comparative study of cavitation characteristics in Si₃N_4p/Al-Mg-Si composite and 7475 aluminum alloy[J]. Scripta Metall Mater, 1994, 31(3): 255?260.

[10] WADA S, MABUCHI M, HIGASHI K, LANGDON T G. A quantitative analysis of cavitation in Al-Cu-Mg metal matrix composites exhibiting high strain rate superplasticity[J]. J Mater Res, 1996, 11(7): 1755?1764.

[11] YAMAMOTO H, NISHIMURA H, MIYAZAKI A. Formability of superplastic aluminum alloy composites reinforced with SiC particles[J]. Mater Proc Tech, 2000, 101(3): 198?208.

[12] MARCINIAK Z, KUCZYNSKI K. Limit strains in the processes of stretch forming sheet metal[J]. Int J Mech Sci, 1967, 9(6): 609?613.

[13] TONG G Q, CHAN K C, NIEH T G. Superplastic bulging of an Al-Mg-0.3Sc alloy and its forming limits[J]. Mater Sci Forum, 2004, 471(5): 385?389.

[14] STOWELL M J. Cavity growth in superplastic alloys[J]. Metal Sci, 1980, 14(7): 267?272.

[15] MAHONEY M W, HAMILTON C H, GHOSH A K. Development of forming limits for superplastic formed fine grain 7475 Al[J]. Metall Trans, 1983, 14(8): 1593?1598.

[16] TAI W H. Predictions of limit strains in sheet metal using a plastic damage model[J]. Int J Mech Sci, 1988, 30(2): 119?126.

收稿日期：2008-03-19；修订日期：2008-06-10

通讯作者：赵祖德，研究员；电话：023-68792238；E-mail: cqzzd@163.com

(编辑 杨华)