DOI: 10.11817/j.issn.1672-7207.2019.01.020

基于Prandtl破坏模式的吸力式沉箱基础抗拔承载力极限分析上限解

朱文波¹，戴国亮^{1, 2}，龚维明^{1, 2}，赵学亮^{1, 2}

(1. 东南大学 土木工程学院，江苏 南京，210096；

2. 东南大学 混凝土及预应力混凝土结构教育重点实验室，江苏 南京，210096)

摘要：为了研究吸力式沉箱基础竖向抗拔荷载作用下极限承载力上限解，引入“反向地基承载力”，基于Prandtl破坏机构，选择合适的地基破坏模式及机动位移速度场，使原Prandtl机构中主动区变为被动区，对数螺旋线反向，并考虑土体自重、黏聚力及土压力因素，推导吸力式沉箱基础抗拔荷载作用下极限承载力上限解。分析上限解与黏聚力、内摩擦角、土压力以及摩擦因数关系，采用Matlab软件编程计算出上限解，并与有关试验值和上限解进行对比分析。研究结果表明：反向Prandtl破坏机构符合实际受力情况。文中上限解与试验值相对误差基本上控制在40%以下，最大相对误差为44%，最小相对误差为3%，接近试验值，证明其破坏模式的合理性及方法的适用性。

关键词：吸力式沉箱基础；Prandtl破坏模式；极限分析；上限定理；能量耗散率

中图分类号：TU473        文献标志码：A         文章编号：1672-7207(2019)01-0158-07

Upper bound solution for ultimate bearing capacity of suction caisson foundation based on Prandtl failure mode

ZHU Wenbo¹, DAI Guoliang^{1, 2}, GONG Weiming^{1, 2}, ZHAO Xueliang^{1, 2}

(1. School of Civil Engineering, Southeast University, Nanjing 210096, China;

2. Key Laboratory of Concrete and Prestressed Concrete Structure of Ministry of Education,

Southeast University, Nanjing 210096, China)

Abstract: In order to study the upper bound solution of the uplift ultimate bearing capacity of suction caisson foundation, the viewpoint of reverse bearing capacity and the reverse Prandtl failure mode were introduced for study. The reverse Prandtl failure mode means that the active area of Prandtl failure mode becomes the passive area and the logarithmic spiral direction was opposite. At the same time, the relationship between the upper bound solution and cohesion, internal friction angle, soil pressure and friction coefficient were analyzed. Then, the upper bound solution was calculated by using the Matlab calculation program and was compared with the previous experimental data and other upper bound solution. The results show that the proposed equations are verified by the corresponded test results. And the upper bound solution agrees reasonably well with the other test results. The error between upper bound solutions and the experimental values are basically controlled to be less than 40%, with the maximum error being 44%, and the minimum error being 3%. It can be proved that the failure mechanism is reasonable and more consistent with the actual force condition.

Key words: suction caisson foundation; Prandtl failure mode; limit analysis; upper bound theorem; energy dissipation rate

吸力式沉箱基础作为海上漂浮式平台的一种锚固基础，常受到竖向抗拔荷载作用，对竖向荷载作用下圆形基础极限承载力与极限分析上限解有不少研究成果，如：TERZAGHI^[1]考虑基础形状、荷载形式、地面形状等因素，对条形基础地基承载力的计算公式进行了修正，使其可用于圆形基础地基承载力计算；CHAKRAHORTY等^[2]分析了圆形基础地基计算公式系数N_γ和基础宽度B的关系；CLAUSEN^[3]基于Hoek-Brown准则研究了圆形基础的地基承载力；LAVASAN等^[4-5]针对改良地基研究了圆形基础的地基承载力；李亮等^[6]根据极限分析中的上限定理，选择合适的机动位移速度场，推导出圆形浅基础受压作用下地基承载力的上限；张国祥等^[7]考虑了单元土体所受的侧向土压力对地基极限承载力的影响，推导出理论上更为合理的三维圆形浅基础地基极限承载力上限解；刘拴奇等^[8]利用临界滑动场法计算了浅埋圆形基础的地基承载力，通过建立土体条块极限平衡方程，推导了计算地基承载力的递推关系式；陈飞等^[9]构建圆形基础多块体离散破坏模式，同时考虑土体自重、黏聚力及边载因素，求得竖向极限承载力上限解；陈中流^[10]采用多切线和多刚块法在非线性破坏准则下，利用极限分析上限理论对圆形基础地基极限承载力进行了求解；王志云^[11]基于Prandtl机构采用“反向地基承载力”的观点，推导了吸力式沉箱基础三维抗拔承载力极限分析上限解。由于Prandtl机构是受压破坏模式，吸力式沉箱基础是抗拔破坏而不是受压破坏，王志云^[11]完全采用Prandtl破坏机构，破坏模式不理想。目前，对吸力式沉箱基础竖向抗拔极限分析研究较少。为了研究吸力式沉箱基础竖向抗拔荷载作用下极限承载力上限解，本文作者引入“反向地基承载力”观点，基于Prandtl破坏机构，从空间问题着手，选择合适的地基破坏模式及机动位移速度场，同时考虑土体自重、黏聚力及土压力因素，推导理论上更为合理的吸力式沉箱基础抗拔承载力极限分析上限解，并与相关文献解进行对比，分析其合理性，为吸力式沉箱基础抗拔极限分析提供参考。

1  机动许可速度场的建立

虚功原理表明^[12]，对于任意一组静力容许的应力场和任意一组机动容许的速度场，外力虚功率等于物体内能消散功率。根据上述原理可推导出上限定理：在所有机动容许的塑性变形速度场相对应的荷载中，极限荷载为最小。根据极限分析上限定理，对直径为D、埋深为L的吸力式沉箱基础，建立机动许可速度场如图1所示，并假定：1) 圆形基础为刚性体，且底面与地基光滑接触，接触面为最小主应力面；2) 地基为理想刚塑性体，满足相关流动法则；3) 地基破坏区分为3部分：刚性体ABC为Ⅰ区，Prandtl破坏模式中Ⅰ区为主动破坏区，文中Ⅰ区为被动破坏区、ACD为过渡变形区、刚性体ADE为主动破坏区；4) 假设作用AE圆环面上土压力等效为q。

图1  反向Prandtl破坏模式

Fig. 1  Reverse Prandtl failure mode

Ⅰ区位移速度场的分布如图2所示。假设基础的向上的速度为v_p，则ABC刚体与沉箱向上垂直运动，其速度也为v_p。由图2所示速度分布图可以推导出AC，CD及DE间断面上的速度。

1) AC间断面上的速度为

              (1)

式中：v_p为基础向上运动速度；φ为地基土内摩擦角；v₀为AC间断面速度。

图2  相容速度图

Fig. 2  Compatible speed chart

2) CD间断面上的速度为

      (2)

式中：θ为v₀与v之间夹角。

3) DE间断面上的速度为

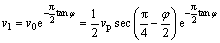     (3)

通过几何关系可以得到

     (4)

式中：R为沉箱半径。

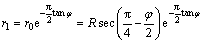       (5)

   (6)

2  上限分析与能量耗散率计算

内能耗散率包括速度间断面上的能量耗散率、变形区能量耗散率、重力作用下的能量耗散率，外功率为极限荷载作用下的虚功率与等效土压力下的虚功率^[12]。间断面的单位面积的能量耗散率可以通过黏聚力c与跨层的切向速度变化v的简单乘积表示。

2.1  圆锥体ACB区

1) 如图1所示，以AC为母线的圆锥间断面ACB上的能量消散率为

 (7)

式中：c为地基土黏聚力；R为沉箱半径。

2) 圆锥体ACB区所受重力做功功率为

         (8)

式中：γ为地基土重度。

3) 圆锥体AB面上能量消散率为0。

2.2  对数螺线ADCFB变形区

1) 旋转间断面DCF上能量消散率为

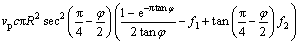      (9)

其中：

     (10)

    (11)

2) 变形区ADCFB内部能量消散率为

    (12)

3) 对数螺旋线变形区速度示意图如图3所示，变形区DCF内所重力做功功率为

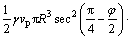
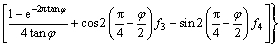 (13)

其中：

  (14)

图3  变形区速度示意图

Fig. 3  Velocity of deformation zone diagram

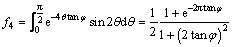    (15)

2.3  三角形AED和BFG区

1) 主动区EDFG间断面上的能量耗散率为

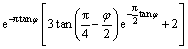       (16)

2) 主动区EDFG的重力做功为

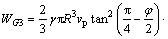
     (17)

3) ADBF面上能量消散率为0。

沉箱外壁与黏附土体界面上的能量耗散率为

            (18)

其中：a为沉箱与土体间的摩擦因数。

重力做功功率为

           (19)

作用在AEBG圆环面上等效土压力q做功功率为

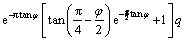      (20)

外荷载做功功率为

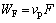               (21)

2.4  极限分析上限解

根据系统的虚功率方程，竖直上拔荷载做功功率与等效土压力做功功率之和等于体系内部内能耗散率，从而得到

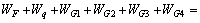
            (22)

化简得上限解F为

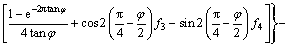
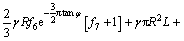
  (23)

其中：

             (24)

             (25)

            (26)

3  计算结果对比分析

吸力式沉箱基础抗拔承载力极限分析上限解主要由外力做功的能量耗散率、速度间断面上及变形区能量耗散率和重力做功的能量耗散率3部分组成，这3部分对吸力式沉箱基础的抗拔承载力上限解贡献有所不同，F为抗拔极限承载力上限解，q为AEBG面上的等效土压力，这2部分为外力，外力之和的能量耗散率等于内能的耗散率，可以得出各部分能量耗散率对上限解的贡献。为分析不同耗散区对上限解的贡献，取重度γ=20 kN/m³，沉箱基础半径R=3 m，沉箱高L=10 m，沉箱与土体界面采用完全粗糙(a=1)，分析不同参数对上限解的影响，结果如图4~6所示。

由图4可以看出：当q=0 kPa时，上限解随内摩擦角的增大而减小；当q=200 kPa时，上限解随内摩擦角的增大而增加；当内摩擦角大于23°时上限解几乎不再增加；黏聚力越大，上限解越大；等效土压力越大，上限解越小。

由图5可以看出：黏聚力随内摩擦角与土压力的不同对上限解影响也有所差异；当q=0 kPa时，黏聚力对上限解影响不大，上限解随黏聚力的增加而增大；当q=100 kPa时，黏聚力对上限解影响不大，上限解随黏聚力的增大而增大；当q=200 kPa时，内摩擦角对上限解影响较大；当内摩擦角c较小时，上限解较低，同时上限解随黏聚力的增加而增大；等效土压力越小，上限解越大。

图4  上限解与内摩擦角的关系曲线

Fig. 4  Relationship between upper bound solution and φ

图5  上限解与黏聚力关系曲线

Fig. 5  Relationship between upper bound solution and c

图6  上限解与等效土压力关系曲线

Fig. 6  Relationship between upper bound solution and q

由图6可以看出：上限解随着等效土压力的增大而减小，这是因为等效土压力与上拔力同为外力，其他参数不变的情况下内部能量耗散率等于外部能量耗散率，所以，AE面上等效土压力q越小，上限解就越大。

表1所示为随不同参数的变化各部能量耗散区提供的承载力与上限解的比例关系。由表1可以看出：沉箱及沉箱内土体所提供的承载力不随q，c和φ的变化而变化；上限解随黏聚力的增大而增大，随土压力的增大而减小。

图7所示为摩擦因数对上限解的影响，计算中取沉箱长为10 m，半径为3 m，土体重度为20 kN/m³。图7中a=0表示沉箱与土体界面完全光滑的计算结果，a=1.0表示沉箱与土体界面完全粗糙计算结果。从图7可见：沉箱与土体界面完全光滑上限解小于沉箱与土体界面完全粗糙上限解，且黏聚力越大，摩擦因数对上限解影响越明显。

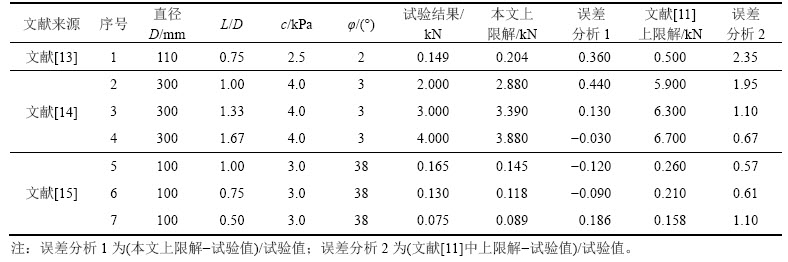
采用文献[13-15]中试验数据以及文献[11]中的吸力式沉箱基础抗拔承载力上限解，用Matlab编制相应计算程序，将式(23)所计算的上限解与其进行对比分析，结果如表2所示。试验数据中均采用吸力式沉箱基础快速上拔的极限承载力，由式(23)计算得沉箱与土体界面完全粗糙时上限解与试验值相对误差个别值有些偏大，但基本上均控制在40%以内，最大相对误差为44%，最小相对误差为3%。由于反向地基破坏模式选取不同，本文采用的上限解要小于文献[11]中完全采用Prandtl破坏模式上限解，更接近试验值。说明文中选取的破坏机构较合理，文中采取上限解是一个更接近极限承载力的上限解。

表1  不同能量耗散区对比分析

Table 1  Comparison of different energy dissipation zones

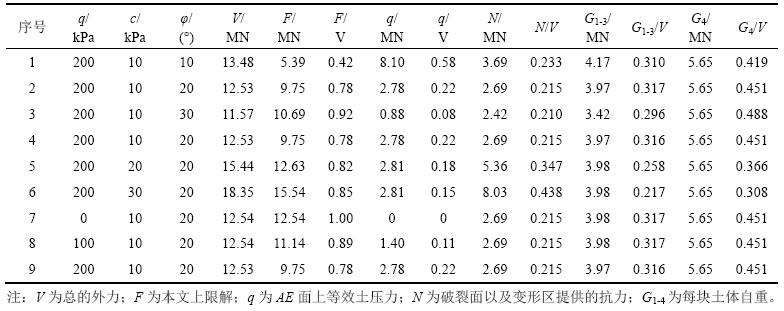
图7  摩擦因数对上限解影响分析

Fig. 7  Influence of friction coefficient on upper limit solution

表2  上限解与其他方法对比分析

Table 2  Comparison upper bound solution with other methods

4  结论

1) 为了研究吸力式沉箱基础竖向抗拔荷载作用下承载力上限解，引入了“反向地基承载力”观点，基于Prandtl破坏机构，将Prandtl破坏机构中的主动区变为被动区，对数螺旋线方向相反，推导了理论上更合理的三维圆形基础抗拔地基极限承载力上限解。

2) 黏聚力越大，上限解越大；等效土压力越大，上限解越小；沉箱与土体界面完全光滑上限解小于沉箱与土体界面完全粗糙上限解，且黏聚力越大，摩擦因数对上限解影响越明显。

3) 由文中上限解推导出的反向地基极限承载力上限解与试验值误差基本上控制在40%以内，最大相对误差为44%，最小相对误差为3%。由于反向地基破坏模式选取的不同，本文采用的上限解要小于完全采用Prandtl破坏模式上限解，更接近试验值。说明文中选取的破坏机构较为合理。文中采取上限解是一个更接近极限承载力的上限解。可为吸力式沉箱基础抗拔极限分析提供参考。

参考文献：

[1] TERZAGHI K. Theoretical soil mechanics[M]. New York: John Wiley and Sons Inc, 1943: 60-76.

[2] CHAKRABORTY D, KUMAR J. Dependency of N_γ on footing diameter for circular footings[J]. Soils and Foundations, 2013, 53(1): 173-180.

[3] CLAUSEN J. Bearing capacity of circular footings on a Hoek-Brown material[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 57(1): 34-41.

[4] LAVASAN A A, GHAZAVI M. Behavior of closely spaced square and circular footings on reinforced sand[J]. Soils and Foundations, 2012, 52(1): 160-167.

[5] ORNEK M, LAMAN M, DEMIRC A, et al. Prediction of bearing capacity of circular footings on soft clay stabilized with granular soil[J]. Soils and Foundations, 2012, 52(1): 69-80.

[6] 李亮, 杨小礼. 圆形浅基础地基承载力极限分析的上限解析解[J]. 铁道学报, 2001, 23(1): 94-97.

LI Liang, YANG Xiaoli. Analytical solution of bearing capacity of circular shallow foundations using upper bound theorem of limit analysis[J]. Journal of the China Railway Society, 2001, 23(1): 94-97.

[7] 张国祥, 付江山. 基于极限分析的圆形浅基础地基承载力上限解[J]. 岩土力学, 2010, 31(12): 3849-3854.

ZHANG Guoxiang, FU Jiangshan. Upper bound solution for bearing capacity of circular shallow foundation based on limit analysis[J]. Rock and Soil Mechanics, 2010, 31(12): 3849-3854.

[8] 刘拴奇, 卢坤林, 朱大勇, 等. 圆形基础地基极限承载力计算[J]. 工程地质学报, 2015(5): 1005-1012.

LIU Shuanqi, LU Kunlin, ZHU Dayong, et al. calculation of ultimate bearing capacity of circular footing[J]. Journal of Engineering Geology, 2015(5): 1005-1012.

[9] 陈飞, 练继建, 王海军. 浅埋圆形基础竖向地基承载力极限分析上限解[J]. 湖南大学学报(自然科学版), 2014, 41(6): 92-98.

CHEN Fe, LIAN Jijian, WAND Haijun. Upper-bound limit analysis of the vertical bearing capacity of circular shallow foundations[J]. Journal of Hunan University(Natural Science Edition), 2014, 41(6): 92-98.

[10] 陈中流. 基于非线性破坏准则的圆形基础地基承载力上限分析[D]. 长沙: 中南大学土木工程学院, 2008: 36-46.

CHEN Zhongliu, Upper bound limit analysis of circular foundation foundations based on non-linear damage criterion[D]. Changsha: Central South University. School of Civil Engineering, 2008: 36-46.

[11] 王志云. 软土地基上吸力式沉箱基础的抗拔承载特性研究[D]. 大连: 大连理工大学土木工程学院, 2008: 58-67.

WANG Zhiyun. A study on uplift bearing characteristics of suction caisson foundation in soft[D]. Dalian: Dalian University of Technology. School of Civil Engineering, 2008: 58-67.

[12] 陈惠发. 极限分析与土体塑性[M]. 北京: 人民交通出版社, 1975: 105-120.

CHEN Huifa. Limit analysis and soil plasticity[M]. Beijing: China Communications Press, 1975: 105-120.

[13] DENG W, CARTER J P. A theoretical study of the vertical uplift capacity of suction caissons[J]. International Journal of Offshore and Polar Engineering, 2002, 12(2): 89-97.

[14] 施晓春, 龚晓南, 俞建霖, 等. 桶形基础抗拔力试验研究[J]. 建筑结构, 2003, 33(8): 49-51.

SHI Xiaochun, GONG Xiaonan, YU Jianlin, et al. Study on buckling resistance of bucket foundation[J]. Building Structure, 2003, 33(8): 49-51.

[15] 矫滨田, 鲁晓兵, 赵京, 等. 吸力式桶形基础抗拔承载力特性试验研究[J]. 中国海洋平台, 2006, 21(3): 27-29.

JIAO Bintian, LU Xiaobing, ZHAO Jing, et al. Experimental study on the uplift bearing capacity of suction bucket foundation[J]. China Ocean Platform, 2006, 21(3): 27-29.

(编辑  杨幼平)

收稿日期：2018-01-02；修回日期：2018-02-06

基金项目(Foundation item)：国家重点研发计划专项项目(2017YFC0703408)；国家自然科学基金资助项目(51678145，51478109) (Project(2017YFC0703408) supported by National Key Research and Development Program; Projects(51678145, 51478109) supported by the National Natural Science Foundation of China)

通信作者：戴国亮，博士，教授，博士生导师，从事地下结构工程研究；E-mail: daigl@seu.edu.cn