Article ID: 1003-6326(2005)03-0606-06
Mathematical modeling of electromagnetic
dimensionless number for electromagnetic casting of metals and its application
WANG Hui(王 辉)1, 2, LI Ting-ju(李廷举)1, JIN Jun-ze(金俊泽)1
(1. Research Center of Foundry Engineering, Dalian University of Technology,
Dalian 116023 China;
2. National Enterprise Technology Center, Wuhan Iron and Steel (Group) Co,
Wuhan 430080, China)
Abstract: In order to estimate the feasibility of electromagnetic casting (EMC) for different metals, a mathematical model named the electromagnetic dimensionless number (EMDN) was presented, and its validity was proved by the experiments of aluminum and Sn-3%Pb alloy. From the experiment and the analysis of EMDN it can be concluded that the EMC of steel can be attained only when the magnetic flux density is larger than 0.09T, while that required for aluminum is only 0.04T. The mathematical expression of the electromagnetic dimensionless number was given out.
Key words: electromagnetic dimensionless number; electromagnetic casting; electromagnetic field; electromagnetic force; magnetic flux density CLC
number: TB97; TG249.7 Document code: A
1 INTRODUCTION
Electromagnetic processing of materials is greatly highlighted due to its outstanding performance to enable the product quality and the productivity to be enhanced, and its potential application to the cost reduction through the energy saving and the stream-lined process[1, 2]. As one of such technologies, the electromagnetic casting technology is considered a potential process to drastically improve the surface quality of its products and to eventually increase the productivity of the continuous casting process. Since early 1970s, the electromagnetic casting has been well established and commercially applied to the aluminum casting process[3-7]. Owing to the advantage of reduction of surface defects[8], refinement of solidified structure[9], there are much basic research and development conducted in order to apply the EMC method to different molten metals, even to the steel.
But the distinct physical properties of different metals, such as electric conductivity, magnetic conductivity and density, make the difference of the electromagnetic force imposed on the surface of the metal and distinct distribution of the magnetic flux in the metals even under the uniform experimental parameters, so that the feasibility of the different metal to achieve electromagnetic casting is distinct. It is essentially difficult to apply the electromagnetic casting process to steel because of its larger density and higher casting speed[10], so that the soft-contact continuous casting of steel becomes one of the basic research of the continuous casting field and many progresses have been made in this field[11, 12].
In order to estimate the ability and the feasibility to achieve electromagnetic casting of steel and compare the feasibility among different metals, a mathematical model named the electromagnetic dimensionless number (EMDN) has been developed on the basis of the principle of the electromagnetic casting. Some experiments have been done using Sn-3%Pb alloy and aluminum to prove the validity of the model. By comparing the feasibility of EMC between steel and Sn-3%Pb alloy, the parameters required for steel and other metals in EMC can be deduced.
2 ESTABLISHMENT OF ELECTROMAGNETIC DIMENSIONLESS NUMBER
The equations describing the electromagnetic field are the Maxwells equations. Assuming that the alternating electromagnetic field is a sinusoidal time variation, the Maxwells equations are shown as follows:
where E is electric field strength, V/m; B magnetic flux density, T; H magnetic field intensity, A/m; J induced current density, A/m2; μ magnetic permeability, H/m; σ electrical conductivity, S/m; ω angular frequency of the electric current, ω=2πf; f frequency of the alternating current field, Hz.
The electric field in Eqn.(1) can be approximately expressed as[13]
E=ωBδ(2)
Substituting Eqn.(2) into Eqn.(1), then the induction current density is
J=σE=σωBδ(3)
Then the electromagnetic force density is
F=J×B=σωB2δ(4)
The electromagnetic force density is
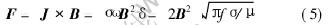
The gravity force density is
p=ρg
In order to achieve the electromagnetic casting, it is necessary for the stability of the meniscus that depends on the equilibrium between the electromagnetic force and the static pressure of the molten metal. As a first approximation, dynamic pressures and surface tension effects can be neglected. Assuming that the height of molten metal confined by electromagnetic force is h, then
Substituting Eqn.(5) into Eqn.(6), then
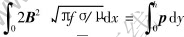
Assuming B[TX-] is the average magnetic flux intensity of the integral distance in the metal surface, then make integral of Eqn.(6) and obtain the following equation:
where t represents the numerical integral region of the electromagnetic body force, which generally should be a small region and here it is chosen as t=5mm. When the skin depth of 
is smaller than 5mm, the integral region of electromagnetic force can be chosen as the skin depth. During the EMC process the height of the molten metal confined by electromagnetic force is generally required of h>40-50mm. Here, it is considered as h=50mm.
Taking all assumption into consideration, then Eqn.(7) can be expressed as
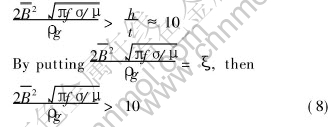
Eqn.(8) is defined as the prerequisite of the electromagnetic casting.
It can be noticed that ξ is a dimensionless number, so that ξ is named the electromagnetic casting dimensionless number or the electromagnetic dimensionless number (EMDN).
Considering the skin effect of the electromagnetic field, then the magnetic flux density in the metal can be expressed as B(x)=B0exp(-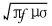 
·x), where B(x) is the magnetic flux density at the x position inside of metal, B0 is the magnetic flux density virtual value at the surface of the molten metal. The average of magnetic flux density in the integral distance can be calculated by
Then substituting Eqn.(9) into Eqn.(8), the EMDN can be expressed as follows:
3 THEORETICAL ANALYSIS AND DISCUSSION
The physical signification of the EMDN model can be considered the ratio between the average electromagnetic force density on the surface of molten metal and its gravity density. The ratio represents the feasibility of metal to achieve the electromagnetic casting. The larger the ratio, the easier the electromagnetic casting.
By comparing the value of EMDN with the prescribed value, the feasibility of the metal to achieve EMC under the given experimental condition can be estimated and some theoretical guidance on the practical experiments can be offered.
The applications of the electromagnetic dimensionless number (EMDN) mainly include:
1) To estimate the feasibility of one metal to achieve EMC under a specific experimental condition.
2) To estimate the minimum of magnetic flux density required for electromagnetic casting of a specific metal under a given experimental condition.
3) To compare the feasibility of different metal to achieve EMC.
Table 1 shows the different physical parameters and electromagnetic parameters of steel, Sn-3%Pb and aluminum in the molten state.
Table 1 Physical and electromagnetic parameters of steel, Sn-3%Pb and aluminum
3.1 EMDN of steel, Sn-3%Pb and aluminum under different frequency and different magnetic flux density
From Table 2 and Table 3 it can be noticed that when the magnetic flux density for aluminum reaches 0.04-0.05T and that for steel and Sn-3%Pb alloy reaches 0.09T, the EMDN becomes larger than 10, so that it can be considered that the electromagnetic casting can be achieved theoretically. Comparing the magnetic flux density under different frequency it also can be noticed that the electromagnetic casting is more easier at a higher frequency.
Table 2 EMDN of three metals under middle frequency (f=2500Hz)
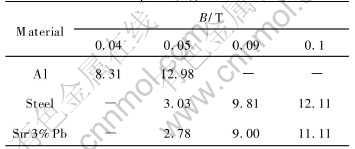
Table 3 EMDN of three metals under high frequency (f=30000Hz)
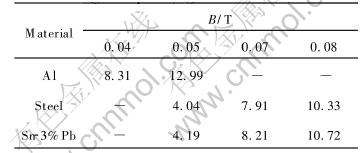
3.2 Effect of experimental parameters on EMDN of metals
Fig.1 shows the effect of frequency on EMDN of steel and Sn-3%Pb alloy while B=0.09T. It can be noticed that the value of EMDN increases with the increase of frequency. When the frequency reaches to some value, the effect on EMDN becomes little.
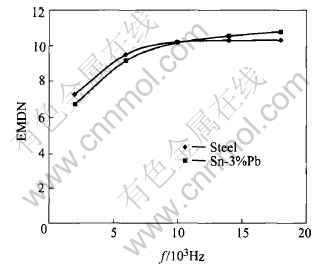
Fig.1 Effect of frequency on EMDN of steel and Sn-3%Pb alloy (B=0.09T)
Fig.2 shows the effect of magnetic flux density on EMDN of steel, Sn-3%Pb and aluminum when f=2500Hz. It can be noticed that the feasibility of metal also increases with the increase of magnetic flux density.
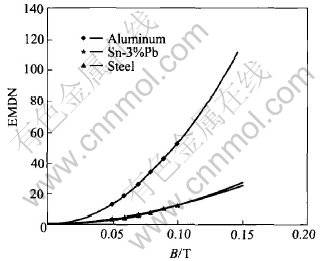
Fig.2 Effect of magnetic flux density on EMDN of aluminum, steel and Sn-3%Pb alloy (f=2500Hz)
Table 4 lists the minimum of magnetic flux density for different metals to achieve EMC when f=2500Hz.
From Fig.2 and Table 4 it can be noticed that the feasibility of EMC of aluminum is larger than that of steel and Sn-3%Pb, while steel has an
Table 4 Comparison of magnetic flux density required for EMC of different metals(f=2500Hz, h=50mm)
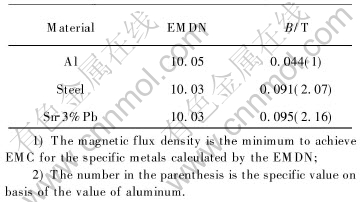
approximately same feasibility as Sn-3%Pb alloy. Under the middle frequency when f=2500Hz, the magnetic flux density for EMC of aluminum is 0.044T while that for EMC of steel and Sn-3%Pb alloy is 0.091T and 0.095T.
3.3 Discussion and summarization
1) The feasibility of metal in EMC can be improved with a higher magnetic flux density and frequency. The effect of the magnetic flux density is larger than that of the frequency, and when the frequency is larger than some value, the effect of it on the feasibility of EMC becomes very little.
2) Under the different frequency the magnetic flux density for one metal to attain EMC will approximately maintain at the same level. Because of the lower electric conductivity, the EMC of steel and Sn-3%Pb can be attained under a relative higher frequency and the magnetic flux density should reach 0.09T or so. While the magnetic flux density for EMC of aluminum only needs about 0.04T.
3) From the analysis above it can be considered that steel and Sn-3%Pb have an approximately uniform feasibility to attain EMC.
4 EXPERIMENTS AND RESULTS ANALYSIS
In order to testify the veracity of the EMDN mathematical model, some experiments on aluminum and Sn-3%Pb alloy have been taken for example.
4.1 Experimental method and experimental apparatus
The experimental power was the middle frequency power apparatus, and the frequency is 2500Hz. The current imposed on the coil can be controlled and it also can be measured by the DT266 Clamp Ampere-meter. The magnetic flux density induced on the coil was measured by a self-made small-induction coil and calculated by the equation as follows:
B=E/(4.44fNS)
where N is the coil quantity; S is the coil-section area, m2. In this experiment, N=10, S=3.14×10-6m2.
4.2 Experimental results and analysis
Fig.3 and Fig.4 illustrate the meniscus shape and column height of aluminum and Sn-3%Pb alloy under different magnetic flux density.
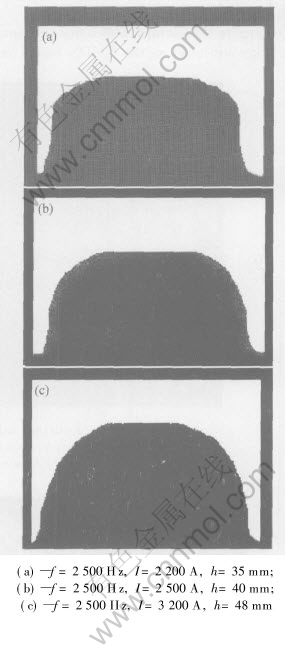
Fig.3 Effect of current on meniscus shape and height of aluminum
Table 5 represents the experiment results of the output current and the measured magnetic flux density of Sn-3%Pb and aluminum respectively.
Table 5 Experimental results
From Fig.3 and Fig.4 it can be noticed that when the magnetic flux density is 0.036-0.04T, the electromagnetic shaping of aluminum can be approximately achieved, but only when the magnetic flux density reaches 0.09T or even larger, the electromagnetic shaping of Sn-3%Pb alloy could be attained approximately.
There is a good agreement between the experiment results and the calculated results by EMDN. Then the validity of the EMDN model in analyzing and estimating the feasibility of EMC for metals is proved.
Owning to the uniform feasibility between Sn-3%Pb alloy and steel as the EMDN model represents, it is practicable to substitute Sn-3%Pb alloy for steel to estimate the feasibility of EMC.
Fig.5 shows the meniscus shape of Sn-3%Pb alloy under the different magnetic flux density.
By the experiments of Sn-3%Pb alloy substituted for steel, it can be deduced that the magnetic flux density required for EMC of steel is approximate 0.09T, which is much larger than that of aluminum (0.04T). Only when the magnetic flux density is larger than 0.09T can the electromagnetic casting of steel be achieved as far as the electromagnetic shaping is concerned.
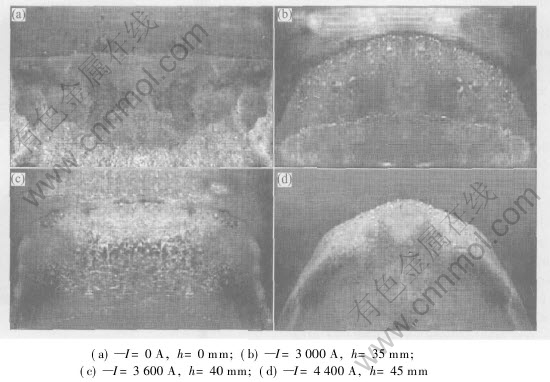
Fig.4 Effect of current on meniscus shape and height of Sn-3%Pb
Fig.5 Relationship between magnetic flux density and meniscus shape of Sn-3%Pb alloy
5 CONCLUSIONS
1) The model of electromagnetic dimensionless number (EMDN) used to estimate the feasibility of EMC for metals was presented, and the validity of the model was proved by the experiments using examples of aluminum and Sn-3%Pb alloy.
2) The feasibility of EMC for metals can be improved under a larger magnetic flux density and a higher frequency. The effect of magnetic flux density on the feasibility of EMC for metals is larger than that of frequency, and when the frequency is lager than some value the feasibility of EMC becomes independent of frequency.
3) From the application of EMDN in the feasibility analysis of EMC for aluminum, steel and Sn-3%Pb alloy, it can be summarized that, aluminum has the best feasibility to achieve EMC among these metals and the required magnetic flux density is 0.04-0.05T; steel and Sn-3%Pb alloy has approximately uniform feasibility to attain EMC and the required magnetic flux density is 0.08-0.1T owing to the specific physical parameters.
4) By the experiments of Sn-3%Pb alloy substituted for steel, it can be deduced that only when the magnetic flux density is larger than 0.08-0.9T can the electromagnetic casting of steel be achieved.
REFERENCES
[1]Tzavaras A A, Brody H D. Electromagnetic stirring and continuous casting—achievements, problems and goals [J]. Journal of Metals, 1984(3): 31-37.
[2]Evans J W. The use of electromagnetic casting for aluminum alloys and other metals [J]. Journal of Metals, 1995(5): 38-41.
[3]Getselev Z N, et al. Method of Continuous and Semicontinuous Casting of Metals and a Plant for Same [P]. US 3467166, 1969.
[4]Getselev Z N. Casting in an electromagnetic field [J]. J Metals, 1971, 23: 38-39.
[5]Vives C. Electromagnetic refining of aluminum alloys by the CREM process: Part Ⅰ. Working principle and metallurgical results[J]. Metall Trans B, 1989, 20(5): 623-629.
[6]Prasso D C, Evans J W, Wilson I J. Heat transport and solidification in the electromagnetic casting of aluminum alloys: Part Ⅰ. Experimental measurements on a pilot-scale caster[J]. Metall Mater Trans B, 1995, 26(6): 1243-1251.
[7]Vives C, Ricou R. Experimental study of continuous electromagnetic casting of aluminum alloys [J]. Metall Trans B,1985, 16: 377-384.
[8]Hayashi N, Nagae K, Nagayama M. Prevention of surface defects on EMC slab [J]. Light Metals, 1995, 1049-1054.
[9]Pritchett T R. Electromagnetic casting of aluminum alloys[J]. Light Metal Age, 1981, 39(9): 12-16.
[10]Nakata H, Etay J. Meniscus shape of molten steel under alternating magnetic field [J]. ISIJ International, 1992, 32(4): 521-528.
[11]Tingju L, Kensuke S, Shigeo A. Surface quality improvement of continuously cast metals by imposing intermittent high frequency magnetic field and synchronizing the field with mold oscillation[J]. ISIJ International, 1996, 36(4): 410-416.
[12]Takehiko T, Eiichi T, Masatake H, et al. Electromagnetic control of initial solidification in continuous casting of steel by low frequency alternating magnetic field[J]. ISIJ International, 1997, 37(11): 1112-1119.
[13]Asai S, Nishio N, Muchi I. Theoretical analysis and model experiments on electromagnetically driven flow in continuous casting[J]. Trans ISIJ, 1982, 22: 126-133.
(Edited by YUAN Sai-qian)
Foundation item: Projects(59995442; 50274017; 50234020) support by the National Natural Science Foundation of China
Received date: 2003-09-16; Accepted date: 2004-09-23
Correspondence: WANG Hui, PhD; Tel:+86-27-86487651; E-mail: stofen2005@yahoo.com.cn; stofen@student.dlut.edu.cn
