J. Cent. South Univ. (2012) 19: 1564-1569
DOI: 10.1007/s11771-012-1177-0
Extended consensus analysis of multi-agent systems with switching topologies
PAN Huan(潘欢)1, NIAN Xiao-hong(年晓红), GUO Ling(郭凌)
School of Information Science and Engineering, Central South University, Changsha 410083, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: Theoretical analysis of consensus for networked multi-agent systems with switching topologies was conducted. Supposing that information-exchange topologies of networked system are dynamic, a modified linear protocol is proffered which is more practical than existing ones. The definition of trajectory consensus is given and a new consensus protocol is exhibited such that multi-agent system achieves trajectory consensus. In addition, a formation control strategy is designed. A common Lyapunov function is proposed to analyze the consensus convergence of networked multi-agent systems with switching topologies. Simulations are provided to demonstrate the effectiveness of the theoretical results.
Key words: networked multi-agent systems; consensus problem; switching topologies; M-matrix
1 Introduction
Recently, consensus problems have been studied extensively in the content of distributed coordinated control of dynamic agents, partly owning to the potential broad application in various areas, including congestion control in communication network, distributed sensor networks, formation control, flocking and swarm analysis and rendezvous problem.
Theoretical framework for posing and solving consensus problems for networked dynamic systems was introduced by OLFATI-SABER and MURRAY [1], based on the pioneering works [2-3]. In Ref. [1], the average-consensus problem was solved with directed graphs, which required the graph to be strongly connected and balanced. REN and BEARD [4] generalized the results of Refs. [1, 3] and presented a more relaxed condition that the topology of directed networks includes a spanning tree. MOREAU [5] studied the non-linear discrete-time multi-agent systems with time-dependent communication channel, and introduced a novel method based on the notion of convexity. XIAO and WANG [6-8] continued to investigate consensus problems in discrete-time multi-agent systems and considered the effect of time delays on consensus. In the past few years, consensus problems of multi-agent systems have been developed rapidly and different forms of agreement problems with differences regarding the types of agent dynamics are addressed, such as asynchronous information consensus [9-10], finite time consensus [11-12], consensus filters [13-14], and network with delays [15-18].
In many applications, the interaction topology between agents may be dynamic due to external disturbances and/or subjected to communication range limitations. For example, communication dropouts occur when a UAV(unmanned aerial vehicle) banks away from its neighbors or through an urban canyon. Therefore, consensus problems with switching topologies have received general attention in application [1, 4, 6, 10-11, 15].
In most literatures, a simple linear time-varying consensus protocol is adopted for multi-agent systems with switching topologies, where each agent updates its information state based on the states of its local time-varying neighbors in such way that the final states of all agents converge to a common value. However, it should be noted that the linear time-varying protocol is not suitable for actual application since it changes time and time again. And for general linear protocols, the final consensus value to be reached is an inherent constant. For example, in Refs. [1, 4], the final consensus value, which depends on both the information-exchange topologies and weights, is a weighted average of the agents’ initial states. A constant preset point is introduced to the consensus algorithm for a directed fixed information-exchange topology. However, a constant final consensus value might not be appropriate in the case that the information sates of each agent are dynamically evolved in the time according to some inherent dynamics as happens in some formation control problems where the formation is moving through space. As a result, it is relevant to study consensus problems where the final consensus value is described as a linear or nonlinear time-varying function.
In this note, some modified linear consensus protocols are proposed which are more practical than existing protocols for multi-agent systems with switching topologies. Using the new protocol, it can be proved that multi-agent system with changed information-exchange topologies converges to a preset point. In order to prove asymptotic convergence to a consensus, a common vector Lyapunov function is introduced which is different from the ones in Refs. [1,15,18]. A definition about trajectory consensus is exhibited, which means that all states of multi-agent system converge to a given time-varying trajectory under switching topologies. Then, a corresponding trajectory consensus protocol is designed, which is used to make the trajectories of all information states agree with the curve of a time-varying nonlinear function. Along with the same line, a formation control protocol is offered to deal with the situation that preset trajectories of each agent are different.
2 Problem formulation
2.1 Definitions and notations
Let G=(V, E, A) be a directed generalized diagram of order n with the set of nodes V={v1, …, vn}, set of edges E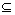 V×V, and a weighted adjacency matrix
V×V, and a weighted adjacency matrix 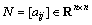 with non-negative adjacency elements aij. The node indexes belong to a finite index set
with non-negative adjacency elements aij. The node indexes belong to a finite index set 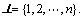 An edge of the weighted digraph G is denoted by
An edge of the weighted digraph G is denoted by 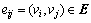 . The set of neighbors of node vi is denoted by
. The set of neighbors of node vi is denoted by 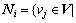
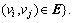 The adjacency elements associated with the edges of the graph are positive, i.e.
The adjacency elements associated with the edges of the graph are positive, i.e. 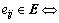 aij>0. Particularly, if node
aij>0. Particularly, if node 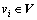 has a self-feedback controller, then aii>0. The union of directed graph G(t) on the time set {t0, t1, …, tk} is a directed graph with constant vertex set as G(t) and the edge set
has a self-feedback controller, then aii>0. The union of directed graph G(t) on the time set {t0, t1, …, tk} is a directed graph with constant vertex set as G(t) and the edge set  . The in-degree and out-degree of node vi are defined as
. The in-degree and out-degree of node vi are defined as
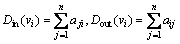
In a multi-agent system, each agent can be considered as a node in a digraph, and the information flow between two agents can be regarded as a directed path between the nodes. Thus, the interconnection topology in a multi-agent system can be described by a directed graph 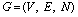 . Let xi denote the value of node vi, Gx=(G, x) is referred with x=(x1, x2, …, xn)T as a network (or algebraic graph) with value
. Let xi denote the value of node vi, Gx=(G, x) is referred with x=(x1, x2, …, xn)T as a network (or algebraic graph) with value  and topology (or information flow) G. Suppose that the time sequence of topology varying is
and topology (or information flow) G. Suppose that the time sequence of topology varying is  tk, …}. In time interval [tk-1, tk), the neighbor set of node vi is denoted as
tk, …}. In time interval [tk-1, tk), the neighbor set of node vi is denoted as 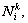
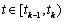 ,
, 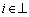 . In this case, the weighted adjacency element sij(t) is a time-varying function that satisfies
. In this case, the weighted adjacency element sij(t) is a time-varying function that satisfies
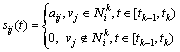 (1)
(1)
Therefore, Gx(t) is a time-dependent directed graph with state 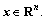 Denote the union of Gx(t) on time set T as
Denote the union of Gx(t) on time set T as 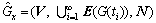 and
and 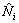 as the neighbors of agent i in digraph
as the neighbors of agent i in digraph 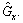
It is said that nodes vi and vi agree in a network if and only if xi=xj for all i, 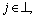 i≠j. Whenever the nodes of a network are all in agreement, the common value of all nodes is called the group decision value. When the final common value is not a fixed value, but a foregone time-varying trajectory, the following definition is obtained.
i≠j. Whenever the nodes of a network are all in agreement, the common value of all nodes is called the group decision value. When the final common value is not a fixed value, but a foregone time-varying trajectory, the following definition is obtained.
Definition 1 (Trajectory consensus): A networked multi-agent system is called to achieve trajectory consensus if and only if all nodes of network converge to a given trajectory 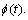
2.2 Consensus protocols
Suppose each node of a digraph is dynamical integrator agent with dynamics
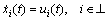 (2)
(2)
where 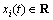 and
and  denote the state and the control input of agent i, respectively.
denote the state and the control input of agent i, respectively.
For multi-agent systems with switching topologies, the following linear consensus protocol has been extensively used to achieve consensus by many researchers:
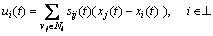 (3)
(3)
where Ni denotes the neighbors of agent i and sij(t) is defined as Eq. (1). Under consensus protocol (Eq. (3)), information state xi(t) is updated based on the information of its local time-varying neighbors.
However, it is worth noticing that consensus protocol (Eq. (3)) has some disadvantages as follows:
1) Protocol needs to accurately detect the information of neighbor multi-agents and switch controllers repeatedly. These operations would bring about some technical problems and enhance some difficulties of controller design for practical system. And repeated switching could arise some side effects for example impulse.
2) Applying consensus protocol, the stability of L matrix will be used in the consensus proof. Nevertheless, the stability of L matrix is a kind of critical stability. In engineering system design, critical stability should be avoided as much as possible since such stability doesn’t have robustness and suffers disturbance easily, resulting in unstable situation.
3) Multi-agent systems would converge to a fixed value by using Eq. (3). But in general, the final control objective is to make multi-agent system converge to a preset trajectory.
For these reasons, a modified protocol is presented as
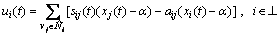 (4)
(4)
where 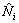 is the neighbor of agent i, aij>0 is the adjacency element in digraph
is the neighbor of agent i, aij>0 is the adjacency element in digraph  the definition of sij(t) is displayed in Eq. (1), and
the definition of sij(t) is displayed in Eq. (1), and 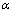 is the convergence point.
is the convergence point.
Obviously, Eq. (4) can avoid repeated switching of controllers and enhance the robustness of system. Based on Eq. (4), a consensus protocol is further designed such that multi-agent systems converge to a preset trajectory or form a formation.
With Eq. (4), system (Eq. (2)) has the following form
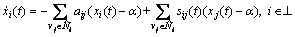 (5)
(5)
In this work, consensus of multi-agent system Eq. (2) under protocol Eq. (4) is mainly investigated by using the properties of M-matrix. Then, the definition of M-matrix is shown as follows.
Definition 2 [19]: Let 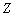 denote the set of square matrices whose off-diagonal elements are non-positive, that is,
denote the set of square matrices whose off-diagonal elements are non-positive, that is,
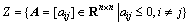
Then, matrix A is called a non-singular (or singular) M-matrix if A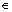 Z and if all its principal minors are positive (or non-negative).
Z and if all its principal minors are positive (or non-negative).
3 Results
Before giving the main results, an available lemma is displayed which will be used in proofs.
Lemma 1 [19]: If matrix 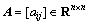 is diagonally dominant (strictly diagonally dominant), i.e.
is diagonally dominant (strictly diagonally dominant), i.e.
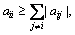 then eigenvalues of A have non-negative
then eigenvalues of A have non-negative
(positive) real parts. Additionally, if A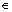 Z, matrix A is a singular (non-singular) M-matrix.
Z, matrix A is a singular (non-singular) M-matrix.
3.1 Consensus of multi-agent systems
The stability proof for multi-agent system Eq. (2) with the consensus protocol Eq. (4) is presented.
Theorem 1: Under the protocol Eq. (4), suppose
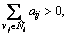 i.e. Dout(vi)>0, i
i.e. Dout(vi)>0, i for directed graph
for directed graph
 system (Eq. (5)) achieves a consensus asymptotically.
system (Eq. (5)) achieves a consensus asymptotically.
Proof: Let yi(t)=xi(t)-α, then closed-loop system (Eq. (5)) is written as
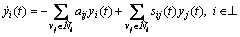 (6)
(6)
From Eq. (6), it is concluded that all states of system (Eq. (5)) reaching an agreement regarding a certain quantity α is equivalent to Eq. (6) converging to zero. Next, it is just needed to prove that system (Eq. (6)) is asymptotically stable about zero for all i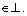 Define a vector Lyapunov function as
Define a vector Lyapunov function as
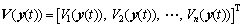 (7)
(7)
with
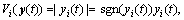 i=1, …, n
i=1, …, n
where sgn(yi(t)) is a signum function, y(t)=[y1(t) y2(t) … yn(t)]T. The time derivative of Vi(y(t)) along any trajectory of Eq. (6) is
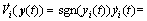

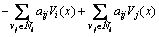
Thus, the following differential inequality is derived:
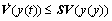
where

From Lemma 1, it is easily seen that -S is a singular M-matrix with rank of n-1, so S is a stable matrix. By the vector comparison theorem, it is declared that system (Eq. (6)) is stable. The proof is ended.
Remark 1: In the proof of Theorem 1, a valid common Lyapunov function Eq. (7) is chosen for stability analysis of system Eq. (6) which is different from the ones used in Refs. [7,9].
When sij(t)=aij, switching structured protocol (Eq. (4)) will become fixed structured protocol. From Theorem 1, the following corollary can be get easily.
Corollary 1: Suppose sij(t)=aij in Eqs. (4) and (5) for
time sequence ^, then under the condition 
Eq. (5) globally asymptotically realizes a consensus.
3.2 Trajectory consensus of multi-agent systems
In practical application, multi-agent systems do not only need to converge to a fixed value but also need to tend to preset time-varying trajectory. Therefore, for a given trajectory f(t) which is assumed to be differentiable, the following trajectory consensus protocol is proposed as
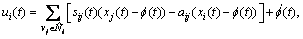
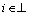 (8)
(8)
where f(t) is a differentiable function.
Under Eq. (8), Eq.(2) is written as
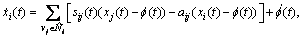
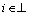 (9)
(9)
where f(t) is a differentiable function.
Theorem 2: For a given trajectory f(t) which is assumed to be differentiable function, suppose
 i.e. Dout(vi)>0,
i.e. Dout(vi)>0, 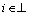 for directed graph
for directed graph 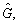
then Eq. (9) achieves a trajectory consensus asymptotically.
Proof: Let  then closed-loop system (Eq. (9)) is transformed into
then closed-loop system (Eq. (9)) is transformed into
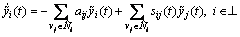 (10)
(10)
Through above transformation, it is obtained that the achievement of trajectory consensus of Eq. (9) is equivalent to Eq. (10) converging to zero for all 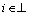 .
.
By using Theorem 1, 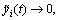
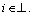 So, it holds that
So, it holds that 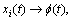
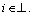 The proof is completed.
The proof is completed.
From Theorem 2, it is concluded that multi-agent system (Eq. (2)) can achieve trajectory consensus under consensus protocol Eq. (8). It is very significant in engineering application, since through designing an appropriate consensus protocol, multi-agent system could reach goal trajectory f(t).
When sij(t)=aij, switching information structure would degenerate fixed information topology. Right now, Eq. (8) becomes a simpler form:
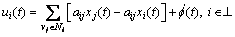 (11)
(11)
where f(t) is a differentiable function. From Theorem 2, following corollary is easily obvious.
Corollary 2: Under Eq. (11), Eq. (2) asymptotically
realizes trajectory consensus if 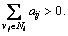
3.3 Formation control of multi-agent system
Sometimes, each agent needs to run different trajectories and forms a formation in multi-agent system. Therefore, for different trajectory φi(t), the following equation is designed:
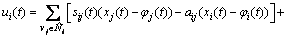
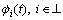 (12)
(12)
where φi(t) is a differentiable function. By using Eq. (12), Eq. (2) is expressed as
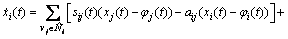
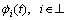 (13)
(13)
where φi(t) is a differentiable function.
Theorem 3: For given trajectory φi(t) which is
assumed to be differentiable, suppose  i.e.
i.e.
Dout(vi)>0 for directed graph 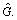 Then, Eq. (13) can form a formation asymptotically.
Then, Eq. (13) can form a formation asymptotically.
Proof: Similar to the proof of Theorem 2, let 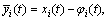 it is derived that
it is derived that 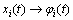 is equivalent to
is equivalent to 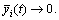 Theorem 1 shows that
Theorem 1 shows that 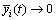 directly. The proof is finished.
directly. The proof is finished.
When sij(t)=aij, switching structured protocol Eq. (12) will become fixed structured protocol. Then, the following corollary is acquired easily.
Corollary 3: Supposing sij(t)=aij in Eqs. (12) and (13) for time sequence ^, then Eq. (13) converges to trajectory
φi(t) asymptotically under the condition  .
.
It is seen from Theorem 3 that single agent tends to different trajectories φi(t) by using Eq. (12). Especially, when φi(t)=f(t)+θi, multi-agent systems would achieve formation control, where f(t) denotes consensus trajectory which is disscussed in Section 3.2 and θi is the location parameter. The set of location parameters {θi, i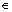 ^} describes the formation of multi-agent system.
^} describes the formation of multi-agent system.
4 Examples and simulation results
Consider the following four different directed graphs each with n=8, which are shown in Fig. 1. For simplicity, it is assumed that all diagraphs in Fig. 1 have weights of 0-1. Figure 2(a) presents the union of switching topologies G1, G2, G3 and G4 denoted by 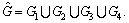 Figure 2(b) shows that multi-agent systems start at the digraph G1 and switch every T=0.1 to other digraph. The out-degrees of
Figure 2(b) shows that multi-agent systems start at the digraph G1 and switch every T=0.1 to other digraph. The out-degrees of  is [1, 4, 3, 1, 2, 3, 4, 2].
is [1, 4, 3, 1, 2, 3, 4, 2].
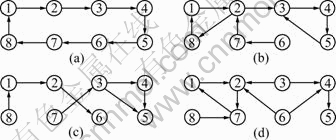
Fig. 1 Four examples of direct graphs: (a) G1; (b) G2; (c) G3; (d) G4
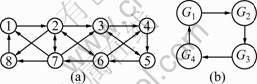
Fig. 2 Union of graphs G1, G2, G3, G4 (a) and switching order (b)
It is obvious that the out-degrees of 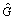 are all greater than zero. As a result, by Theorem 1, networked system Eq. (5) with switching topologies G1, G2, G3 and G4 realizes a consensus. Figure 3 shows the simulation result under consensus protocol Eq. (4) with α=4.
are all greater than zero. As a result, by Theorem 1, networked system Eq. (5) with switching topologies G1, G2, G3 and G4 realizes a consensus. Figure 3 shows the simulation result under consensus protocol Eq. (4) with α=4.
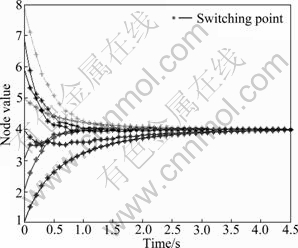
Fig. 3 State trajectories of all nodes corresponding to switching topologies
For a given trajectory f(t)=cos t+sin 3t, which is described in Fig. 4 for 0≤t≤6, Eq. (8) is used such that multi-agent system tends to f(t). Figure 5 depicts multi-agent system Eq. (9) achieving trajectory consensus.
When the goal trajectories are different for each agent, multi-agent system forms a formation for φi(t) under Eq. (12). For simplicity, choose φi(t)=f(t)+θi, where f(t) is the consensus trajectory and θi is the location parameter. Let f(t)=cos t+sin 3t, and θ1=-0.6, θ2=-0.4, θ3=-0.2, θ4=0, θ5=0.2, θ6=0.4, θ7=0.6, θ8=0.8. Then the state trajectories of multi-agent system (Eq. (13)) is shown in Fig. 6 corresponding to switching topologies G1, G2, G3 and G4.
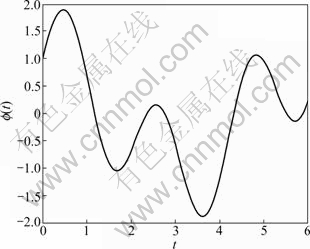
Fig. 4 Preset trajectory of f(t)
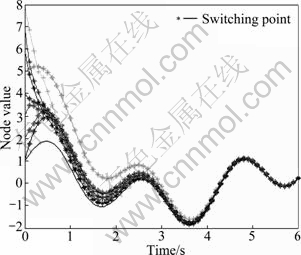
Fig. 5 State trajectories of all nodes converging to f(t) with switching topologies

Fig. 6 State trajectories of all nodes attaining formation with switching topologies
5 Conclusions
1) The convergence analysis of some consensus protocols for a network of integrators is provided with directed information flow and switching topologies. The analysis relies on several tools from algebraic graph, matrix theory, and control theory.
2) The concept of trajectory consensus is defined. Correspondingly, new consensus analysis strategies are proposed which make all states of multi-agent systems with switching topologies converge to a preset point, a foregone trajectory and form a formation respectively.
3) To develop consensus analysis, a common Lyapunov function is introduced. The sufficient conditions that the multi-agent systems with switching topologies reach a consensus are obtained. The results show that if the out-degrees in union graph of switching graphs are all greater than zero, the networked systems with switching topologies can realize consensus. Extensive simulation results are given in order to demonstrate the effectiveness of the theoretical results and analytical tools.
References
[1] OLFATI-SABER R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays [J]. IEEE Transaction on Automatic Control, 2004, 49(9): 1520-1533.
[2] VICSEK T, CZIRóK A, BEN-JACOB E, COHEN I, SHOCHET O. Novel type of phase transition in a system of self-driven particles [J]. Physical Review Letters, 1995, 75(6): 1226-1229.
[3] JADBABAIE A, LIN J, MORSE A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules [J]. IEEE Transaction on Automatic Control, 2003, 48(9): 988-1001.
[4] REN W, BEARD R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies [J]. IEEE Transactions on Automatic Control, 2005, 50(5): 655-661.
[5] MOREAU L. Stability of multiagent systems with time-dependent communication links [J]. IEEE Transaction on Automatic Control, 2005, 50(2): 169-182.
[6] XIAO Feng, WANG Long. State consensus for multi-agent systems with switching topologies and time-varying delays [J]. International Journal of Control, 2006, 79(10): 1277-1284.
[7] XIAO Feng, WANG Long. Dynamic behavior of discrete-time multiagent systems with general communication structures [J]. Physica A, 2006, 370(2): 364-380.
[8] WANG Long, XIAO Feng. A new approach to consensus problems in discrete time multiagent systems with time-delays [J]. Science in China Series F: Information Sciences, 2007, 50(4): 625-635.
[9] FANG Lei, ANTSAKLIS Panos J. Asynchronous consensus protocols using nonlinear paracontractions theory [J]. IEEE Transaction on Automatic Control, 2008, 53(10): 2351-2355.
[10] XIAO Feng, WANG Long. Asynchronous consensus in continuous- time multi-agent systems with switching topology and time-varying delays [J]. IEEE Transaction on Automatic Control, 2008, 53(8): 1804-1816.
[11] JIANG Fang-cui, WANG Long. Finite-time information consensus for multi-agent systems with fixed and switching topology [J]. Physica D, 2009, 238(16): 1550-1560.
[12] WANG Long, XIAO Feng. Finite-time consensus problems for networks of dynamic agents [J]. IEEE Transaction on Automatic Control, 2010, 55(4): 950-955.
[13] HUI QING, HADDAD Wassim M. Distributed nonlinear control algorithms for network consensus [J]. Automatica, 2008, 44(9): 2375-2381.
[14] YU Wen-wu, CHEN Guang-rong, WANG Zi-dong, YANG Wen. Distributed consensus filtering in sensor networks [J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics, 2009, 39(6): 1568-1577.
[15] SUN Yuan-gong, WANG Long, XIE Guang-ming. Average consensus in networks of dynamic agents with switching topologies and multiple time-varying delays [J]. Systems & Control Letters, 2008, 57(2): 175-183.
[16] TIAN Yu-ping, LIU Cheng-lin. Consensus of multi-agent systems with diverse input and communication delays [J]. IEEE Transaction on Automatic Control, 2008, 53(9): 2122-2128.
[17] XIAO Feng, WANG Long. Consensus protocols for discrete-time multi-agent systems with time-varying delays [J]. Automatica, 2008, 44(10): 2577-2582.
[18] SUN Yuan-gong, WANG Long. Consensus of multiagent systems in directed networks with nonuniform time-varying delays [J]. IEEE Transaction on Automatic Control, 2009, 54(7): 1607-1613.
[19] QU Zhi-hua. Cooperative control of dynamic systems: Applications to autonomous vehicles [M]. London: Springer-Verlag, 2009: 167- 172.
(Edited by DENG Lü-xiang)
Foundation item: Projects(61075065, 60774045) supported by the National Natural Science Foundation of China; Project(CX2010B080) supported by Hunan Provincial Innovation Foundation For Postgraduate, China
Received date: 2011-02-25; Accepted date: 2011-05-09
Corresponding author: NIAN Xiao-hong, Professor, PhD; Tel: +86-13549668182; E-mail: xhnian@mail.csu.edu.cn