
DOI: 10.11817/j.issn.1672-7207.2020.06.006
阀控电液位置伺服系统滑模反步控制方法
吉鑫浩1,汪成文1, 2,陈帅1,张震阳1
(1. 太原理工大学 机械与运载工程学院,山西 太原,030024;
2. 浙江大学 流体动力与机电系统国家重点实验室,浙江 杭州,310058)
摘要:针对阀控电液位置伺服系统的非匹配干扰抑制问题,将滑模控制理论与反步递推控制器设计方法相结合,提出一种滑模反步递推控制方法;在滑模反步递推控制算法设计过程中,提出一种新的光滑连续的滑模控制律;对所提控制算法的稳定性及跟踪误差的收敛性进行理论及定量分析,并对该控制方法的可行性及有效性进行联合仿真验证。研究结果表明:该算法能够有效抑制未知非匹配干扰与输出抖动,其跟踪效果明显优于反步控制器以及PID控制器的跟踪效果。
关键词:电液伺服系统;非匹配干扰;反步法;滑模控制;位置控制
中图分类号:TP273 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207(2020)06-1518-08
Sliding mode back-stepping control method for valve-controlled electro-hydraulic position servo system
JI Xinhao1, WANG Chengwen1, 2, CHEN Shuai1, ZHANG Zhenyang1
(1. School of Mechanical and Vehicle Engineering, Taiyuan University of Technology, Taiyuan 030024, China;
2. State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University,Hangzhou 310058, China)
Abstract: A sliding mode back-stepping control method was proposed for the mismatched disturbances in valve-controlled electro-hydraulic position servo system. A new smooth and continuous sliding mode control law was applied to the design of sliding mode back-stepping control algorithm. The stability of the proposed control algorithm and the convergence of tracking error were theoretically and quantitatively analyzed. The feasibility and validity of the control method were verified by co-simulation. The results show that the algorithm can effectively suppress unknown mismatched disturbances and output chattering. Compared with back-stepping controller and PID controller, it has better tracking effect.
Key words: electro-hydraulic servo system; mismatched disturbances; back-stepping method; sliding mode control; position control
电液伺服系统具有功重比高的优点,能在有限的空间里输出更大的力或力矩,被广泛应用于挖掘机[1]、隧道掘进机[2]、工业机器人[3]和电液负载模拟器[4-6]等。然而,在实际应用中,电液伺服系统经常受到非匹配干扰力如摩擦力、随机外负载干扰力等的作用,对系统的控制精度有重要影响。因非匹配干扰与系统输入不在同一个状态方程中,通过控制系统输入无法直接处理非匹配干扰,所以,如何抑制非匹配干扰的问题一直是工业界和学术界的研究热点与难点。目前,一些控制方法已经被用于处理非匹配干扰问题。WANG等[6]针对负载模拟器力矩跟踪系统,通过反步法实现了对系统中非匹配的多余力与摩擦力的补偿,有效抑制了非匹配干扰力对系统的影响。石胜利等[7]设计了一种基于干扰观测器的反步位置跟踪控制器,实现了对外部扰动的实时补偿,并解决了传统反步控制中存在的计算膨胀问题。李浩等[8]提出一种反步非奇异快速终端滑模控制方法,即先通过反步法有效抑制了系统中非匹配干扰的影响,在反步法最后一步构造快速终端滑模消除匹配干扰力对系统的影响,该方法对匹配与非匹配干扰都具有一定的鲁棒性。CHOI[9]使用LMI(linear matrix inequality)方法设计了线性滑模面,使得滑模对一类特殊的非匹配扰动具有不变性。YANG等[10]设计了连续终端滑模控制器,并利用有限时间干扰观测器估计非匹配干扰,实现了估计误差在有限时间内收敛,有效抑制了非匹配干扰。WANG等[11]利用状态观测器实现了对存在未知外部常值干扰和参数不确定性的系统的渐进跟踪。郑剑飞等[12-13]提出一种高阶终端滑模控制方法,有效抑制了系统中的匹配与非匹配干扰,并且提高了收敛速度和跟踪精度,消除了控制“抖振”。CAO等[14]设计了一种积分滑模,通过高精度的切换增益使系统状态到达滑模,该方法有效地抑制了系统中的非匹配干扰,但易导致滑模控制中的“抖振”问题。蒲明等[15]针对高阶非线性系统,利用高阶滑模微分器作为间接干扰观测器,估计系统中的非匹配复合干扰,然后设计递阶Terminal滑模控制器,理论上能够实现系统跟踪误差任意小。GUAN等[16-17]使用自适应滑模控制方法实现了对阀控系统与泵控系统的控制,即利用反步自适应方法处理参数不确定性,并通过滑模控制方法处理反步自适应的误差与外界干扰力,但该控制方法针对的参数不确定性与外界干扰都是匹配的。反步法是一种常用的非线性设计方法,其思想是依据李雅普诺夫稳定性定理设计系统各状态的虚拟控制器,从而实现对系统的控制。使用反步法能有效补偿系统中的非匹配干扰,但其依赖于系统精确的数学模型,而滑模控制对系统数学模型精度不敏感,可完全消除匹配干扰对系统的影响,但难以处理非匹配干扰。针对反步法依赖于系统精确的数学模型与滑模控制难以处理非匹配干扰的研究现状,本文作者提出一种滑模反步控制方法,通过设计一种新的光滑连续一阶可导的滑模控制律,解决滑模控制方法与反步控制方法之间的设计冲突,为滑模与反步法的结合提供理论依据;然后,利用李雅普诺夫稳定性判定方法证明算法的稳定性与最大跟踪误差的收敛性;最后,以阀控电液位置伺服系统为研究对象,对算法进行联合仿真,验证控制策略对未知数学模型的非匹配干扰与控制输出“抖振”的抑制效果,并与PID控制器、反步控制器进行比较。
1 系统描述
1.1 阀控电液位置伺服系统组成
阀控电液位置伺服系统构成如图1所示。阀控电液位置伺服系统通过控制伺服阀的阀芯位移来实现对液压缸活塞位置的控制。

图1 阀控电液位置伺服系统示意图
Fig. 1 Schematic diagram of valve-controlled electro-hydraulic position servo system
1.2 阀控电液位置伺服系统数学模型
对称液压缸的动态可以被描述为
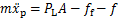 (1)
(1)
式中:m为负载的质量;xp为液压缸活塞的位移;PL=P1-P2,为负载压力;P1为液压缸左腔压力;P2为液压缸右腔压力;A为液压缸活塞的有效面积;ff为摩擦力;f为随机外负载力与未建模非匹配干扰力的合力。
流量连续性方程推导过程基于以下假设:
1) 使用的伺服阀是匹配对称的理想零开口阀;
2) 滑阀与液压缸的外泄不计;
3) 供油压力恒定;
4) 系统的总压缩容积在系统运行过程中不变。
基于以上假设可得系统的流量连续性方程[18]为
 (2)
(2)
式中:QL为负载流量;Ct为系统总的内泄漏系数;βe为油液体积弹性模量;Vt为系统的总压缩容积。
负载流量与阀芯位移之间的关系[18]为
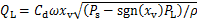 (3)
(3)
式中:Cd为伺服阀的流量系数;ω为伺服阀的面积梯度;xv为阀芯位移;Ps为供油压力;ρ为油液密度。
因伺服阀的动态特性参数值远高于所研究系统的动态特性参数值,所以,伺服阀的动态被忽略,有
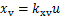 (4)
(4)
式中:kxv为伺服阀的增益;u为控制输出。
sgn(x)定义了一个不连续的符号函数:
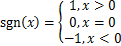 (5)
(5)
选取活塞位移xp、线速度 以及负载压力PL为系统的状态变量,即x=[x1,x2,x3]=[xp,
以及负载压力PL为系统的状态变量,即x=[x1,x2,x3]=[xp, ,PL]。结合式(1)~(5)可得系统的动态方程为
,PL]。结合式(1)~(5)可得系统的动态方程为
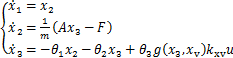 (6)
(6)
式中: ,为摩擦力与随机外负载力、未建模的非匹配干扰力的合力;
,为摩擦力与随机外负载力、未建模的非匹配干扰力的合力;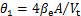 ;
;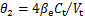 ;
;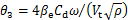 ;
; 。
。
在动态方程(6)中,F为未知数学模型的非匹配干扰,对系统的位置跟踪精度有重要的影响,本文的目的是给定一个参考的位置轨迹xd,设计滑模反步控制律去生成一个控制输出u,有效抑制F对系统的影响,使得系统输出y=x1以较高的精度跟踪参考轨迹xd。
2 控制器设计与稳定性证明
将滑模控制理论与反步递推控制器设计方法相结合设计滑模反步控制器,并证明控制算法的稳定性以及最大跟踪误差的收敛性。控制器的设计过程基于以下假设:
1) 参考位置轨迹3阶可导;
2) 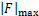 有界;
有界;
3) 参数 与
与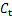 在系统运行过程中不变。
在系统运行过程中不变。
在式(6)所示的动态方程组中,F位于第2个方程式中,为非匹配干扰,通常的做法是采用反步法来补偿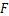 的影响,但F的数学模型未知,传统反步法达不到预期效果。考虑前2个方程式,若将第2个方程式中的x3看作虚拟控制输出,则F相对于x3为匹配干扰,因此采用滑模控制方法得到的理想x3可完全消除F对系统的影响。x3的虚拟控制器的设计采用滑模设计方法,设计过程如下。
的影响,但F的数学模型未知,传统反步法达不到预期效果。考虑前2个方程式,若将第2个方程式中的x3看作虚拟控制输出,则F相对于x3为匹配干扰,因此采用滑模控制方法得到的理想x3可完全消除F对系统的影响。x3的虚拟控制器的设计采用滑模设计方法,设计过程如下。
定义xd为参考位置轨迹,定义位置跟踪误差e1为
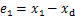 (7)
(7)
定义滑模函数S为
 (8)
(8)
式中:λ为正常数。
S对于时间的导数为
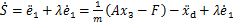 (9)
(9)
若将式(9)中的x3看作滑模控制输出,则等效的负载压力x3eq可设计为
 (10)
(10)
由等效负载压力x3eq可设计对于x3的虚拟控制量x3d即期望的负载压力,因后续设计要求x3d对时间连续可导,而传统的滑模控制律因使用符号函数,使得x3d在S=0时对时间的导数不存在,为保证x3d对时间连续可导,本文提出一种新的光滑连续一阶可导的滑模控制律。
当|S|≥ξ,x3d被设计为
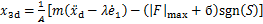 (11)
(11)
当|S|<ξ,x3d被设计为
 (12)
(12)
式中: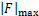 用于消除摩擦力与随机外负载力、未建模非匹配干扰力对系统的影响;б为一个大于零的常数,可适当加快S的收敛速度;ξ为一足够小的正数。
用于消除摩擦力与随机外负载力、未建模非匹配干扰力对系统的影响;б为一个大于零的常数,可适当加快S的收敛速度;ξ为一足够小的正数。
式(11)和(12)中,在|S|<ξ的范围内用光滑连续的函数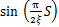 代替符号函数,既保证滑模控制律x3d对时间连续可导,满足算法推导的条件,同时也使得x3d光滑连续,抑制了滑模控制的抖动。此外,本文提出的新的滑模控制律还有利于算法稳定性证明与跟踪误差收敛性的定量分析。
代替符号函数,既保证滑模控制律x3d对时间连续可导,满足算法推导的条件,同时也使得x3d光滑连续,抑制了滑模控制的抖动。此外,本文提出的新的滑模控制律还有利于算法稳定性证明与跟踪误差收敛性的定量分析。
由式(11)可得当|S|≥ξ,x3d对时间的导数为
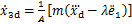 (13)
(13)
由式(12)可得当|S|<ξ,x3d对时间的导数为

 (14)
(14)
定义x3与x3d之间的误差e3为
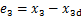 (15)
(15)
定义李雅普诺夫函数V1为
 (16)
(16)
则V1对时间的导数为
 (17)
(17)
剩余的任务是通过反步设计方法由x3d推导出真正的控制输出u,并证明控制算法的稳定性。由式(3)与式(4)可知,真正的控制输出u由负载压力与负载流量共同决定,所以,首先由x3d推导出期望的负载流量QLd。由式(2)可得:
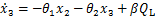 (18)
(18)
式中: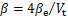 。
。
定义李雅普诺夫函数V为
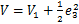 (19)
(19)
当|S|≥ξ,V对时间导数为

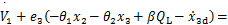

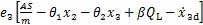 (20)
(20)
为保证系统稳定性,令
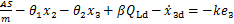 (21)
(21)
式中:k为一个正常数。
则可得期望的负载流量QLd为
 (22)
(22)
然后,由期望的负载流量QLd与负载压力x3来导出真正的控制输出u。由式(3)与式(4)可知导出u的主要困难是确定参数Cd与ω,这些参数与伺服阀的结构有关,往往无法获得精确值。
伺服阀额定流量Qr的计算公式为
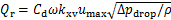 (23)
(23)
式中: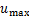 为伺服阀的最大控制输入;
为伺服阀的最大控制输入; 为伺服阀额定压降。
为伺服阀额定压降。
由式(3),(4)和(23)可得控制器实际的控制输出为
 (24)
(24)
最后,证明系统的稳定性与最大跟踪误差的收敛性。当|S|≥ξ,期望的负载流量QLd可保证式(25)恒成立,且只在ei(i=1,3)=0时等号成立,所以系统收敛。
 (25)
(25)
当|S|<ξ,V对时间导数为
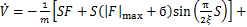
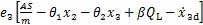
 (26)
(26)
此时,QLd虽然不能保证式(25)恒成立,但由式(8)可知,其引起的最大位置跟踪误差 为
为
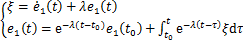 (27)
(27)
式中:t0为系统第一次到达|S|=ξ的时刻;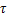 为积分变量。
为积分变量。
因λ>0,e1(t0)为一有限常数,则当时间趋于无穷时,可得最大位置跟踪误差为
 (28)
(28)
从频域的角度对误差的收敛性进行分析,也可以得到相同的结论,对式(27)作拉氏变换得:
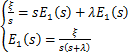 (29)
(29)
式中:s为拉普拉斯算子;E1(s)为e1(t)的拉氏变换。
由终值定理可得,当时间趋于无穷时系统最大位置跟踪误差为
 (30)
(30)
由式(28)与式(30)可知,理论上可通过选择合适的ξ和λ使得系统最大位置跟踪误差任意小。所以,采用本文中的滑模反步控制策略可以保证系统的稳定性与最大跟踪误差的收敛性。
综上,阀控电液位置伺服系统的滑模反步控制器设计与稳定性、跟踪误差的收敛的理论证明已经完成,控制器计算过程图如图2所示。

图2 控制器计算过程图
Fig. 2 Diagram of controller computing process
3 仿真研究
为验证滑模反步控制器对未知非匹配干扰与控制输出抖振的抑制效果,对算法进行仿真研究。仿真研究在基于AMESim和Matlab/Simulink的联合仿真平台上进行。联合仿真模型如图3所示。阀控电液位置伺服系统模型在AMESim中搭建,仿真过程中算法在Matlab/Simulink中计算。仿真模型中考虑了内泄、摩擦力、外负载力等对系统的影响,其中摩擦力、外负载力为未知非匹配干扰。
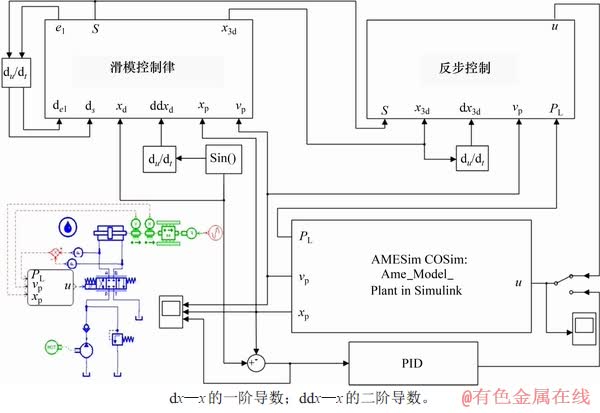
图3 联合仿真模型
Fig.3 Co-simulation model
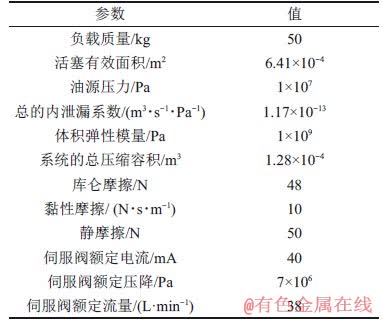
仿真模型的主要参数如表1所示。仿真的采样间隔设置为0.001 s。
所选参考位置信号为: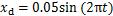 。外部干扰力信号在0 s时加入,系统中的摩擦力与所加干扰力在算法设计过程中作为有界未知干扰力,在0 s所加外部干扰力信号为:
。外部干扰力信号在0 s时加入,系统中的摩擦力与所加干扰力在算法设计过程中作为有界未知干扰力,在0 s所加外部干扰力信号为: 。加入此干扰力是为了验证控制器对未知非匹配干扰的抑制作用。
。加入此干扰力是为了验证控制器对未知非匹配干扰的抑制作用。
PID控制器因结构简单且具有较强的适应性与鲁棒性,被广泛应用到工业生产中;反步控制器常被用于处理非匹配干扰。为验证滑模反步控制器对未知非匹配干扰的抑制效果,将滑模反步控制器与PID控制器、反步控制器进行对比研究。控制器参数选择3个控制器各自表现较好的参数值。其中PID控制器参数KP=3 000,KI=1 500,KD=0;反步控制器参数选择为k1=200,k2=600,k3=300;滑模反步控制器的参数选择为λ=300,ξ=0.3,σ=800,k=350。
表1 仿真模型参数
Table 1 Parameters of simulation model
3个控制器的控制结果对比与控制输出对比分别如图4~6所示。
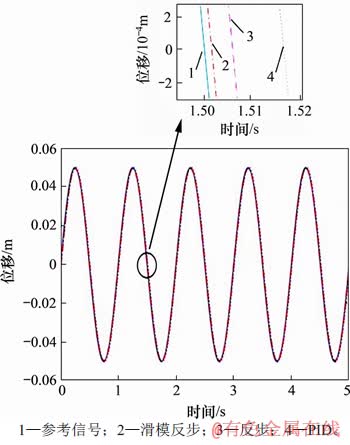
图4 不同控制器跟踪结果对比图
Fig. 4 Comparison of simulation results of different controllers
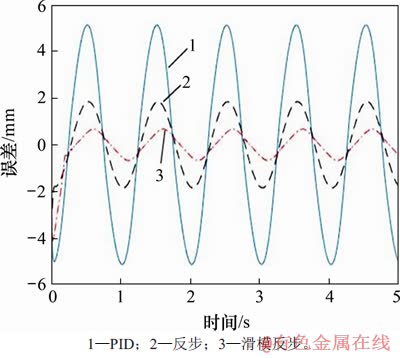
图5 不同控制器跟踪误差对比图
Fig. 5 Error comparison of different controllers
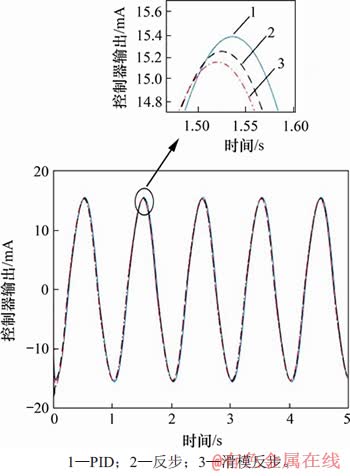
图6 不同控制器控制输出对比图
Fig. 6 Contrast of control output of different controllers
由图4和图5可见:在考虑了摩擦力、外负载干扰力等未知非匹配干扰情况下,在整个控制过程中滑模反步控制器对未知非匹配干扰的抑制效果最好,反步控制器次之,PID控制器最差。由图6可见:滑模反步控制输出稳定后不存在抖动现象,这是由于采用本文提出的新的光滑连续的滑模控制律,可有效地抑制控制输出的抖动。
为定量分析3个控制器的控制效果以及确保对比环境的公平性,定义以下3个参数:
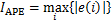 (31)
(31)
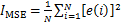 (32)
(32)
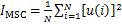 (33)
(33)
式中:e(i)为第i次采样时的跟踪误差;N为记录的跟踪误差数据个数;u(i)为第i次采样时的控制输出值;IAPE为最大的稳态跟踪误差绝对值,IAPE越大控制效果越差;IMSE为稳态跟踪误差均方值,IMSE越大控制效果越差;IMSC为控制输出均方值,可以反映控制器输出信号的强度。
计算得到所定义的各控制器指标如表2所示。
表2 控制器评价指标
Table 2 Parameters of controller evaluation
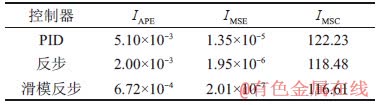
由表2可知滑模反步控制器的IAPE与IMSE明显比PID控制器与反步控制器的小,且IMSC为三者之中的最小值,说明在控制器输出强度较小的情况下,滑模反步控制器的控制效果明显优于PID与反步控制器的控制效果。这是因为PID控制器是利用输入与输出的偏差进行控制的,只考虑了系统输入与输出对系统的影响,因此,计算的IAPE与IMSE最大,控制效果最差;反步控制器通过设置虚拟控制器,使得系统的状态都达到期望值,考虑了系统中的各个状态,因而具有更好的控制效果,但在未知系统精确数学模型的情况下,其控制效果并不理想;滑模反步控制器融合了滑模控制与反步控制的优点,在未知系统精确数学模型的情况下,依然具有良好的控制效果。
4 结论
1) 滑模反步控制算法能够有效抑制系统中的未知非匹配干扰,其控制效果相比PID控制器与反步控制器分别提高了87.7%和66.4%。
2) 本文提出的新的光滑连续滑模控制律不仅为滑模控制与反步法的结合提供理论依据,而且也有效地抑制了滑模控制中存在的输出抖振问题。
3) 通过Lyapunov理论证明了该算法的稳定性与跟踪误差的收敛性。理论上,该算法能够实现跟踪误差任意小。
参考文献:
[1] 董致新, 黄伟男, 葛磊, 等. 泵阀复合进出口独立控制液压挖掘机特性研究[J]. 机械工程学报, 2016, 52(12): 173-180.
DONG Zhixin, HUANG Weinan, GE Lei, et al. Research on the performance of hydraulic excavator with pump and valve combined separate meter in and meter out circuits[J]. Journal of Mechanical Engineering, 2016, 52(12): 173-180.
[2] WANG Lintao, GONG Guofang, YANG Huayong, et al. The development of a high-speed segment erecting system for shield tunneling machine[J]. ASME Transactions on Mechatronics, 2013, 18(6): 1713-1723.
[3] PI Yangjun, WANG Xuanyin. Trajectory tracking control of a 6-DOF hydraulic parallel robot manipulator with uncertain load disturbances[J]. Control Engineering Practice, 2011, 19(2): 185-193.
[4] 汪成文, 焦宗夏, 罗才瑾. 基于改进的速度同步控制的电液负载模拟器[J]. 航空学报, 2012, 33(9): 1717-1725.
WANG Chengwen, JIAO Zongxia, LUO Caijin. An improved velocity synchronization control on electro-hydraulic load simulator[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(9): 1717-1725.
[5] WANG Chengwen, JIAO Zongxia, QUAN Long. Nonlinear robust dual-loop control for electro-hydraulic load simulator[J]. ISA Transactions, 2015, 59: 280-289.
[6] WANG Chengwen, JIAO Zongxia, WU Shuai, et al. Nonlinear adaptive torque control of electro-hydraulic load system with external active motion disturbance[J]. Mechatronics, 2014, 24(1): 32-40.
[7] 石胜利, 李建雄, 方一鸣. 具有输入饱和的电液伺服系统反步位置跟踪控制[J]. 中南大学学报(自然科学版), 2016, 47(10): 3369-3374.
SHI Shengli, LI Jianxiong, FANG Yiming. Backstepping position tracking control for electro-hydraulic servo system with input saturation[J]. Journal of Central South University(Science and Technology), 2016, 47(10): 3369-3374.
[8] 李浩, 窦丽华, 苏中. 非匹配不确定系统的自适应反步非奇异快速终端滑模控制[J]. 控制与决策, 2012, 27(10): 1584-1587, 1592.
LI Hao, DOU Lihua, SU Zhong. Adaptive backstepping non-singular fast terminal sliding mode control for mismatched uncertain systems[J]. Control and Decision, 2012, 27(10): 1584-1587, 1592.
[9] CHOI H H. An LMI-based switching surface design method for a class of mismatched uncertain systems[J]. IEEE Transactions on Automatic Control, 2003, 48(9): 1634-1638.
[10] YANG Jun, LI Shihua, SU Jinya, et al. Continuous nonsingular terminal sliding mode control for systems with mismatched disturbances[J]. Automatica, 2013, 49(7): 2287-2291.
[11] WANG Chengwen, QUAN Long, JIAO Zongxia, et al. Nonlinear adaptive control of hydraulic system with observing and compensating mismatching uncertainties[J]. IEEE Transactions on Control Systems Technology, 2018, 26(3): 927-938.
[12] 郑剑飞, 冯勇, 杨旭强. 非匹配不确定多变量系统高阶终端滑模控制[J]. 电机与控制学报, 2009, 13(1): 117-122.
ZHENG Jianfei, FENG Yong, YANG Xuqiang. High-order terminal sliding mode control of mismatched uncertain multivariable systems[J]. Electric Machines and Control, 2009, 13(1): 117-122.
[13] ZHENG Jianfei, FENG Yong. High-order terminal sliding mode based mechanical resonance suppressing method in servo system[C]// 2nd International Symposium on Systems and Control in Aerospace and Astronautics. Shenzhen, China: IEEE, 2008: 1-6.
[14] CAO W J, XU J X. Nonlinear integral-type sliding surface for both matched and unmatched uncertain systems[J]. IEEE Transactions on Automatic Control, 2004, 49(8): 1355-1360.
[15] 蒲明, 吴庆宪, 姜长生, 等. 非匹配不确定高阶非线性系统递阶Terminal滑模控制[J]. 自动化学报, 2012, 38(11): 1777-1793.
PU Ming, WU Qingxian, JIANG Changsheng, et al. Recursive terminal sliding mode control for higher-order nonlinear system with mismatched uncertainties[J]. Acta Automatica Sinica, 2012, 38(11): 1777-1793.
[16] GUAN Cheng, PAN Shuangxia. Adaptive sliding mode control of electro-hydraulic system with nonlinear unknown parameters[J]. Control Engineering Practice, 2008, 16(11): 1275-1284.
[17] YIN Xiuxing, LIN Yonggang, LI Wei, et al. Adaptive sliding mode back-stepping pitch angle control of a variable-displacement pump controlled pitch system for wind turbines[J]. ISA Transactions, 2015, 58: 629-634.
[18] MERRITT H E. Hydraulic Control Systems[M]. New York, USA: John Wiley & Sons Inc, 1967:79-85.
(编辑 伍锦花)
收稿日期: 2019 -09 -11; 修回日期: 2019 -11 -12
基金项目(Foundation item):山西省重点研发计划项目(201903D121069);流体动力与机电系统国家重点实验室开放基金课题资助项目(GZKF-201720);山西省回国留学人员科研教研资助项目(HGKY2019016) (Project(201903D121069) supported by the Key Research and Development Program of Shanxi Province; Project(GZKF-201720) supported by the Open Foundation of the State Key Laboratory of Fluid Power and Mechatronic Systems; Project(HGKY2019016) supported by Shanxi Scholarship Council of China)
通信作者:汪成文,博士,副教授,从事电液伺服控制研究;E-mail:cwwang@yeah.net