Dynamic explicit FE modeling of hot ring rolling process

WANG Min(王 敏), YANG He(杨 合), SUN Zhi-chao(孙志超),

GUO Liang-gang(郭良刚), OU Xin-zhe(欧新哲)

College of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China

Received 29 February 2006; accepted 18 July 2006

Abstract: A new FE modeling method of hot ring rolling was presented by solving key technologies such as contact and heat boundary conditions, motion control over guide rolls, and mass scaling. The method has the following features: 1) the elastic-plastic dynamic explicit approach instead of the static implicit approach is adopted to solve the process so as to greatly improve computational efficiency without sacrificing computational accuracy; 2) the coupled thermal-mechanical effect is considered as opposed to the conventional isothermal assumption，which is more practical; 3) in contrast to the simplified 2D or local 3D ring model, the full 3D ring is modeled to simulate the process. Based on the FE modeling method, two cases of hot plain ring rolling are simulated in the FEA software ABAQUS/Explicit. The simulation results are compared with the experimental measurements and the good agreement between them is observed regarding the material flow and the temperature distribution of the ring.

Key words: hot ring rolling; dynamic explicit approach; coupled thermal-mechanical; FEM

1 Introduction

Ring rolling is an advanced process typically used to manufacture parts with revolved geometries. It makes use of rotating rolls to press a ring continuously and locally, causing the wall thickness of the ring to reduce, the diameter to expand and the cross-section to shape, as shown in Fig.1.

Fig.1 Schematic diagram of ring rolling

Hot ring rolling, as an important branch of ring rolling, is commonly used to manufacture large rings and ring blanks for further mechanical processes. It is characterized by 3D deformation, high nonlinearity, con-tinuously progressive forming, asymmetry, unsteady- state, etc. Furthermore, during the process, there exits notable heat exchange between the ring and surroundings, and meanwhile plastic work as well as friction work is converted to heat energy, which makes the temperature of the ring change continuously. And the change in temperature will remarkably affect the deformation behavior, microstructure and mechanical properties of the ring. Therefore, how to rapidly and accurately simulate and reveal the process has become an important and troublesome subject in this field.

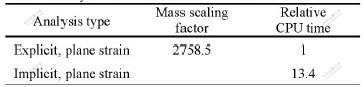
Some research on hot ring rolling has been done using the FEM. In the simulation, the process was treated as either an isothermal[1,2] or a 2D problem[3,4], or only the roll gap region was modeled[5,6]. These simplified treatments not only lead to unacceptable errors, but also cannot reveal the nature of the process. LIM et al[7] performed a coupled thermal-mechanical full 3D analysis of hot ring rolling using the static implicit approach, but claimed that the computational efficiency was still low although there was a 70% improvement in computation time by employing the hybrid mesh technique. In contrast to the implicit approach, the dynamic explicit approach can both save solution costs for large-scale problems and overcome convergence difficulties for highly nonlinear problems, thus offering an effective means for solving metal forming processes. A 2D thick plate rolling process was solved by the explicit and implicit approaches. The results revealed that the explicit case gave essentially the same results as the implicit calculation, only consuming about one- thirteenth of the CPU time, as shown in Table 1[8]. XIE et al[9] carried out a hot ring rolling simulation with the rigid visco-plastic dynamic explicit approach, but the coupled thermal-mechanical effect was not considered. Therefore, up to now, there has been scant literature concerning with the coupled thermal-mechanical simulation of the process using the dynamic explicit approach. This paper begins with a new FE modeling method of hot ring rolling, followed by simulations of two cases of hot plain ring rolling in the FEA software ABAQUS/Explicit, and the simulation results are compared with the experimental measurements.

Table 1 Analysis cases and relative CPU time

2 Coupled thermal-mechanical method of dynamic explicit approach

The heat transfer equations are integrated using the explicit forward-difference time integration rule:

                         (1)

where  θ^N is the temperature at node N and the subscript i refers to the increment number in an explicit dynamic step. The values of are computed at the beginning of the increment by

                       (2)

where  C^NJ is the lumped capacitance matrix, P^J is the applied nodal source vector, and F^J is the internal flux vector.

The equations of motion for the body are integrated using the explicit central-difference integration rule:

                   (3)

                         (4)

where  u^N is a degree of freedom (a displacement or rotation component) at node N and the subscript  is the increment number in an explicit dynamics step. The accelerations at the beginning of the increment are computed by

                     (5)

where  M^NJ is the mass matrix, P^J is the applied load vector, and I^J is the internal force vector.

Since both the forward-difference and central- difference integrations are explicit, the heat transfer and mechanical solutions are obtained simultaneously by an explicit coupling. Therefore, no iterations or tangent stiffness matrices are required.

The explicit procedure is integrated through time by using many small time increments. The central- difference and forward-difference operators are condi- tionally stable. The stability limit for both operators (with no damping in the mechanical solution response) is obtained by choosing

                (6)

where  Δt is the time increment, Δt_stable is the stability limit, w_max is the highest frequency in the system of equations of the mechanical solution response, and λ_max is the largest eigenvalue in the system of equations of the thermal solution response.

3 FE modeling and key technologies

3.1 Geometry model and discretization

Comparing with the ring, the variations of the deformation and temperature of the rolls are so small that the rolls are treated as isothermal rigid bodies. Defining the rolls with analytical rigid surfaces benefits from more accurate geometric description, cheaper computational costs and less noisy contact.

Because the ring is symmetric with respect to the rolling plane, only the upper half is modeled with symmetry constraint applied on the plane. The coupled thermal-mechanical hexahedron element with eight nodes is selected to discretize the ring uniformly. Reduction integration as well as hourglass control is applied to elements to save computation time and avoid the zero-energy mode caused by the bending mode of deformation. The adaptive meshing technology based on the Arbitrary Lagrangian-Eulerian(ALE) method is utilized to reduce element distortion and maintain a high-quality mesh throughout the analysis.

3.2 Material model

The material of the ring adopts elastic-plastic constitutive model and the flow stress is strongly dependent on the strain, strain rate and temperature. The thermal conductivity, specific heat, thermal expansion coefficient and elastic modulus are all temperature dependent.

3.3 Contact and heat boundary conditions

In order to establish the dynamic contact, contact pairs are defined between the ring and driver roll, idle roll as well as guide rolls. There exists friction and contact heat conduction at the interface of each contact pair. Relative sliding existing between the ring and rolls contributes to describe the friction with Coulomb friction model. The friction at the ring-guide rolls interfaces is not considered due to the small friction force. At each contact interface, it is assumed that half of the heat dissipated as a result of friction is conducted into the ring. Ninety percent of the nonrecoverable work from plastic deformation is assumed to heat the ring.

At the surfaces of the ring, convection and thermal radiation are considered. The symmetry plane of the ring is assumed to be adiabatic.

3.4 Motion control over guide rolls

The motion control over guide rolls plays a critical role in developing the FE model of hot ring rolling. It can be effectively realized by controlling the velocities of guide rolls.

The velocities of guide rolls are closely related to the growing velocity of the ring, so the latter is investigated first. Assuming no side spread and that the contours of the ring remain in circular shapes throughout the whole process, an expression can be obtained according to the constant volume condition in the plastic deformation

                       (7)

where  R₀ and r₀ are the outer radius and inner radius of the undeformed ring, respectively; R and r are the outer radius and inner radius of the deforming ring, respectively. We know

                                (8)

                                 (9)

where  H₀ and H are the thickness of the undeformed and deforming rings, respectively.

Substituting Eqns.(8) and (9) into Eqn.(7) yields

                    (10)

The time derivative of Eqn.(10) is

           (11)

where  v_R is the growing velocity of the outer radius of the ring. Let

                                  (12)

where  v denotes the feed rate of the roll. Eqn.(12) indicates that the thickness reduction velocity of the ring is assumed to be equal to the feed rate of the roll, so we have

                               (13)

Substituting Eqns.(12) and (13) into Eqn.(11) gives

                    (14)

It is assumed that the relative position between guide rolls and ring maintains unchanged throughout the whole process. Namely, the angle between the links of the ring’s center O with the idle roll’s center O₁ and with the guide roll’s center O₂, α, is constant, as shown in Fig.2. So the velocity of the guide roll can be obtained with the growing velocities of the outer radius of the ring in the illustrated two directions in Fig.2. The two v_R are projected to 1 and 3 directions

                          (15)

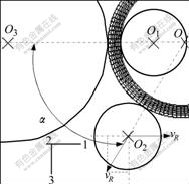
Fig.2 Position of guide roll

However, considering the side spread is neglected, Eqn.(15) should be modified as

                        (16)

where  k ranging from 0 to 1 is the modification factor.

α is selected as 60?[10], and k is determined as 0.7 by the dichotomy method, so the velocities of guide rolls at any time can be solved in terms of Eqns.(14) and (16). Upon writing these discretized velocity-time pairs into ABAQUS, the motion control over guide rolls can be realized.

3.5 Mass scaling

Adopting the dynamic explicit approach, most forming analyses require too much computer time to be run in their physical time scale because the actual time period of forming events is large by dynamic explicit standards. Artificially increasing the mass of the material, which is called mass scaling, can increase the stability limit, so allow the analysis to take less computer time.

In the following simulations, the mass of the entire ring is scaled to 400 times the actual mass to obtain an economical solution.

However, virtual inertial effect resulting from mass scaling may lead to erroneous solution under some circumstances. So the results from the explicit dynamic approach should be evaluated before further investigation. As a general rule, the kinetic energy of deforming material should not exceed a small fraction (typically 5% to 10%) of its internal energy throughout most of the process, and moreover the two energy histories should be smooth and reasonable, so an acceptable quasi-static solution can be obtained[11].

Based on the above FE modeling method, two cases of hot plain ring rolling are simulated in the FEA software ABAQUS/Explicit, and the simulation results are compared with the experimental measurements.

4.1.1 Simulation conditions

The coupled thermal-mechanical full 3D FE model for Case 1 is shown in Fig.3. In Fig.3, the driver roll is driven to rotate around its stationary axis at a constant velocity, the freely mounted idle roll moves at a constant feed rate toward the driver roll, while the guide rolls have a specified motion track in the rolling plane so that they always contact the ring with appropriate pressure to maintain the stability of the operation and the roundness of the ring. The simulation conditions are summarized in Table 2[12].

The material of the ring is tellurium lead. Tellurium lead is sensitive for strain rate and similar to the flow of steel in hot forming, so it is widely used in experiments to model real processes[12]. The flow stress of tellurium lead is represented by[13]

      (17)

where  σ is the flow stress, ε is the strain, andis the strain rate.

4.1.2 Energy of ring

Fig.4 shows the histories of the internal and kinetic energies of the ring. It can be seen that the two are

Fig.3 FE model for Case 1

Table 2 Simulation conditions for Case 1

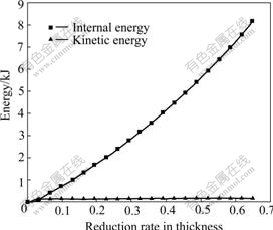
Fig.4 Histories of internal and kinetic energies

smooth; the kinetic energy increases to a certain value at the biting stage, and then remains approximately fixed, which indicates the start of the stable forming stage. In the view of the above rule, an acceptable quasi-static solution has been obtained.

4.1.3 Material flow of ring

The cross-section of the final ring is illustrated in Fig.5. There is obvious “fishtail” shape at the end-plane. Moreover, the side spread at both inside and outside surfaces is slightly smaller than that in the adjacent regions, as marked by the loops in Fig.5. This arises mainly from the friction and contact heat conduction existing at the ring-rolls interfaces. The defect formation as shown is in agreement with that observed by XU et al[14] and is common in an actual open pass ring rolling process without axial rolls.

Fig.6 shows the measured[12] and predicted histories of the maximum outside spread, the maximum inside spread and the minimum spread at the end-plane. It can be seen that the measured and predicted results show reasonable agreement. All side spread increases

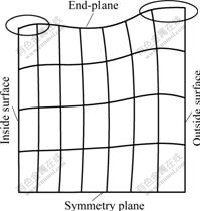
Fig.5 Cross-section of final ring

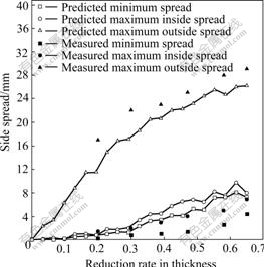
Fig.6 Measured and predicted side spread histories

with time, and the increasing rate of the maximum outside spread decreases while the increasing rates of the maximum inside spread and the minimum spread increase with time. It is expected that the agreement between the measured and predicted results becomes better with finer mesh of the ring.

Fig.7 shows the measured[12] and predicted histories of the ratio of outer diameters which is defined as the ratio of outer diameter of the deforming ring to that of the undeformed ring. In Fig.7, the predicted result is consistent with the measured result. As the process progresses, the growing rate of the outer diameter of the ring becomes faster and faster.

Fig.7 Measured and predicted histories of ratio of outer diameters

4.2.1 Simulation conditions

The coupled thermal-mechanical full 3D FE model for Case 2 is shown in Fig.8. In Fig.8, both the driver roll

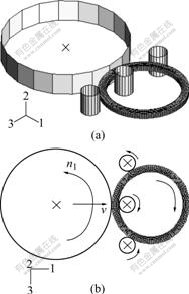
Fig.8 FE model for Case 2

and idle roll are driven to rotate around their axes at constant velocities, and the driver roll moves at a constant feed rate toward the idle roll which has a stationary axis, while the motion tracks of guide rolls are similar to that in Case 1. The simulation conditions are summarized in Table 3[4].

Table 3 Simulation conditions for Case 2

The material of the ring is IN718 Ni-based superalloy. Its temperature dependence of properties and constitutive model are from Ref.[4].

4.2.2 Energy of ring

Fig.9 shows the histories of the internal and kinetic energies of the ring. It can be concluded that an acceptable quasi-static solution has been obtained.

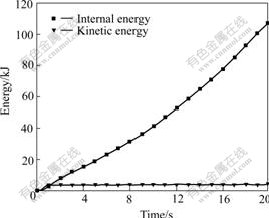
Fig.9 Histories of internal and kinetic energies

4.2.3 Temperature distribution of ring

Fig.10 represents the temperature distribution of the ring during the process. It is found that the temperature at the surfaces, especially at the outside and inside surfaces, decreases with time, while the temperature in the center layer on the symmetry plane is slightly higher than the initial value. This is because the former is dramatically affected by the heat losses due to contact conduction, convection, and radiation, but the latter is primarily influenced by the heat generation due to plastic deformation. It can also be seen from Fig.10 that the temperature variation is more apparent in the radial direction than in the circumferential and axial directions.

Fig.10 Contours of temperature distribution: (a) 3.6 s; (b) 10 s; (c) 20 s

On the symmetry plane of the ring, 3 points situated on the downstream side of the roll gap are selected along the radial direction, as shown in Fig.11. Fig.12 illustrates the measured and predicted temperature histories. In Fig.12, the predicted temperature at point 1 is consistent with the measured result[4] at the outside surface. The discrepancies between them may arise from the constitutive model and calculation error in simulation, the measurement error in experiment, etc. It is can also be seen from Fig.12 that the temperature at point 1 decreases faster than that at point 3, which results from the lower temperature of the driver roll relative to the idle roll and the ever larger contact area between the ring

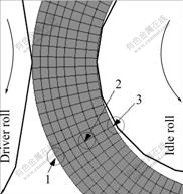
Fig.11 Positions of 3 points

Fig.12 Measured and predicted temperature histories

 and driver roll. Also, the temperature at point 2 first rises and then falls. This is because at first, the heat generation from plastic deformation dominates, and then the heat balance in the ring outweighs the heat generation.

5 Conclusions

A new FE modeling method of hot ring rolling has been discussed. The method is characterized by coupled thermal-mechanical full 3D model combined with the elastic-plastic dynamic explicit approach. Through the simulations of two cases of hot plain ring rolling in the FEA software ABAQUS/Explicit, the predicted material flow and temperature distribution of the ring are compared with experimental results and the agreement between them is good. The method can lend itself to studying the forming laws of hot ring rolling and simulating hot complex profile ring rolling. It is also expected that the method may be applied to other rotation forming technologies with minor modifications.

[1] DAVEY K, WARD M J. A practical method for finite element ring rolling simulation using the ALE flow formulation [J]. International Journal of Mechanical Sciences, 2002, 44: 165-190.

[2] YEA Y S, KO Y S, KIM N K, LEE J C. Prediction of spread, pressure distribution and roll force in ring rolling process using rigid-plastic finite element method [J]. Journal of Materials Processing Technology, 2003, 140: 478-486.

[3] JOUN M S, CHUNG J H, SHIVPURI R. An axisymmetric forging approach to perform design in ring rolling using a rigid-viscoplastic finite element method [J]. International Journal of Machine Tools & Manufacture, 1998, 38: 1183-1191.

[4] SONG J L, DOWSON A L, JACOBS M H, BROOKS J, BEDEN I. Coupled thermo-mechanical finite-element modeling of hot ring rolling process [J]. Journal of Materials Processing Technology, 2002, 121: 332-340.

[5] XU Si-guang, CAO Qi-xiang, LIAN Jia-chuang. Simulation of ring rolling using thermal rigid-plastic finite element model [J]. Chinese Journal of Mechanical Engineering, 1994, 30(2): 87-92. (in Chinese)

[6] XU S G, WEINMAM K J, YANG D Y, LIAN J C. Simulation of the hot ring rolling process by using a thermo-coupled three-dimensional rigid-viscoplastic finite element method [J]. Journal of Manufacture Science and Engineering, 1997, 119: 542-549.

[7] LIM T, PILLINGER I, HARTLEY P. A finite-element simulation of profile ring rolling using a hybrid mesh model [J]. Journal of Materials Processing Technology, 1998, 80/81: 99-205.

[8] ABAQUS Example Problems Manual (version 6.4) [M]. ABAQUS Inc, 2003.

[9] XIE Chun-lei, DONG Xiang-huai, LI Shang-jian, et al. Rigid- viscoplastic dynamic explicit FEA of the ring rolling process [J]. International Journal of Machine Tools and Manufacture, 2000, 40: 81-93.

[10] XU Si-guang, LIAN Jia-chuang. Best position of guide rolls in ring rolling [J]. Metal Forming Machinery, 1991(6): 22-25. (in Chinese)

[11] Getting Started with ABAQUS (version 6.4) [M]. ABAQUS Inc, 2003.

[12] MAMALIS A G, HAWKYARD J B, JOHNSON W. Spread and flow patterns in ring rolling [J]. International Journal of Mechanical Sciences, 1976, 18: 11-16.

[13] KIM N, MACHIDA S, KOBAYASHI S. Ring rolling process simulation by the three dimensional finite element method [J]. International Journal of Machine Tools and Manufacture, 1990, 30(4): 569-577.

[14] XU Si-guang, WANG Hai-wen, LI Guo-zhen. Lateral deformation of the ring in its rolling process [J]. Heavy Machinery, 1990(1): 40-44. (in Chinese)

(Edited by YUAN Sai-qian)

Foundation item: Project(50335060) supported by the National Natural Science Foundation for Key Program of China; Project(50225518) supported by the National Science Fund of China for Distinguished Young Scholars

Corresponding author: YANG He; Tel: +86-29-88495632; E-mail: yanghe@nwpu.edu.cn; sprit418@mail.nwpu.edu.cn