基于蛙跳算法的改进支持向量机预测方法及应用

宋晓华¹，杨尚东²，刘达¹

 (1. 华北电力大学 经济与管理学院，北京，102206；

2. 国网能源研究院 科研发展部，北京，100052)

摘要：针对支持向量机在中长期负荷预测中关键参数选择的问题，引入蛙跳算法(SFLA)以优化基于支持向量机的中长期负荷预测算法，解决支持向量机参数选择问题。以对中国能源消费总量预测为例，对本文提出的改进算法进行验证。以1979—1999年的能源消耗量作为样本，对2000—2009年能量消耗量进行检验。研究结果表明：引入蛙跳算法后，与用粒子群(PSO)算法改进的支持向量机以及普通支持向量机方法相比，改进支持向量机预测精度分别提高2.34%和3.21%，算法运行时间分别增加51 s和109 s。

关键词：支持向量机；蛙跳算法；预测方法

中图分类号：TU457；TU413.6       文献标志码：A         文章编号：1672-7207(2011)09-2737-04

Improved support vector machine forecasting model by shuffled frog leaping algorithm and its application

SONG Xiao-hua¹, YANG Shang-dong², LIU Da¹

 (1. North China Electric Power University, Economic and Management Institute, Beijing 102206, China;

2. State Grid Energy Research Institute, Research and Development Department, Beijing 100052, China)

Abstract: By introducing the shuffled frog leaping algorithm to solve the random-choice problem of the key parameters, the new support vector machine optimized was proposed. In order to verify the optimized effect, based on the training exampling energy demand from 1979 to 1999, the improved SVM was used to forecast the total energy demand of China in 2000—2009. The results show that compared to the normal PSO-SVM and SVM responsively, the time of the improved SVM increases by 51 s and 109 s, and the precision of the proposed method increases by 2.34% and 3.21%, respectively.

Key words: support vector machine; shuffled frog leaping algorithm; forecasting model

中长期能源需求总量预测是谋划能源工业科学发展的重要基础性工作。能源需求总量的变化受到多种复杂因素的影响，如何提升其预测的准确性一直吸引着众多学者关注和研究。传统研究方法多基于统计学的多元线性回归或时间序列方法，这些方法对于趋势性因素的模拟比较精确，但是，难以模拟复杂因素对于中长期负荷变化的影响^[1]。自20世纪90年代以来，人工神经网络方法逐步被应用到中长期能源需求预测中^[2]。最近，有研究者利用群智能算法来改进支持向量机的学习机制，以进一步提升算法学习能力和预测模型的精度。支持向量机预测的效果在很大程度上受到其核函数中关键参数选择的影响^[3]，为此，本文作者提出应用蛙跳算法，以解决支持向量机关键参数盲目选择问题，提高算法的预测效果。通过对2001—2009年中国能源需求总量进行预测，并将本文提出算法(SFLA-SVM)与用PSO改进的支持向量机以及普通支持向量机回归预测模型(SVM)进行比较，以验证蛙跳算法引入后，对解决支持向量机核函数关键参数的选择所产生的改进效果。

1  蛙跳算法

2003年，Eusuff等^[4]在粒子群算法的基础上，结合混合竞争进化(Shuffled complex evolution, SCE)提出了蛙跳算法(Shuffled frog leaping algorithm, SFLA)。这是一种受自然生物模仿启示而产生的基于群体的协同搜索方法^[4]。该算法模拟青蛙群体寻找食物时按族群分类进行信息传递的过程，在同一族群内进行局部深度搜索，离食物源最远的青蛙将主要依据族群内距离食物源最近的青蛙提供的信息调整自己的位置，向食物源靠近。每隔一段时间，不同族群会进行全局信息交换，并根据当前的青蛙状态，重新构成新的族群。以上局部搜索与全局信息交换过程更替进行，直至寻找到食物为止。蛙跳算法将确定性竞争进化策略与有限度随机搜索有机结合^[5-7]。确定性策略保证该算法可以有效利用所获信息指导粒子(青蛙)的随机搜索过程。该算法具有概念简单、参数少、计算速度快、全局寻优能力强、易于实现等优点，与粒子群算法、蚁群算法等群智能搜索方法相比，能够更好地与支持向量机进行融合，提高算法应用的效率与效果。蛙跳算法的机理、模型和算法实现见文献[8-9]。

蛙跳算法的主要参数^[10]有：青蛙群体数N，子群数N₁，混合操作前族群内的更新代数和混合迭代次数。第i只青蛙的位置向量可以表示为X_i=(X_i1, X_i2, …, X_ij)(其中，j为变量的个数)。将种群内青蛙个体适应度降序排列。将整个青蛙群体分为N₁个子群体，每个子群体包括B只青蛙，则N=BN₁。其中：第1，2，…，N₁只青蛙分别进入第1，2，…，N₁个子群体中 ，第N₁+1个青蛙进入第1个群体，如此类推，直到青蛙分配完为止。

每个子群体适应度最高的个体为X_g，适应度最低的个体为X_b，整个青蛙群体的最优值为X_all，对每个子群体进行局部搜索可提高最低个体适应度。蛙跳步长更新策略为：

           (1)

，-S_max≤S_i≤S_max      (2)

式中：rand( )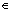[0, 1]；S_max为青蛙所允许改变位置的最大值。

经更新计算后，若得新解X_B+1，则用其取代X_B，重复执行更新策略，求解全局最优解X_all；若所得解无改进，则随机产生一个新解替代所求个体的解，算法继续迭代，直至设定迭代次数为止。本文混合蛙跳算法的参数设置为N=150，N₁=9，族内更新次数为10，混合迭代次数为1 000。

2  支持向量机预测核函数关键参数的选择

2.1  支持向量机原理

支持向量机(Support vector machine, SVM)是由Vapnik提出的一种机器学习方法，是基于结构风险最小化原理的机器学习方法^[11]，能够比较充分利用有限学习样本获得较强泛化能力的决策函数。其算法是一个凸二次优化问题^[12]，以保证算法找到的解是全局最优解，可以较好地解决小样本、非线性、维数灾等问题，解决神经网络方法存在的收敛速度慢和局部极值问题，目前，已经广泛地应用于预测、回归、分类和模式识别问题的解决中。在具体应用过程中，存在一个突出问题，即如何选择关键参数。支持向量机的参数选择决定了其学习能力和泛化能力。

2.2  支持向量机的关键参数

付阳等^[13]经过分析认为，对支持向量机学习能力有影响的主要参数有：惩罚因子c，核函数及其核宽度σ和函数拟合误差ε。惩罚因子c用于控制模型复杂度和逼近误差的折中，c越大，则对数据的拟合程度越高，学习及其复杂度就越高，容易出现“过学习”现象。而c取值若小，则机器复杂度过低，会出现“欠学习”问题^[14]。核宽度σ与学习样本输入空间的范围有关，样本越大，取值越大；样本空间越小，取值越小。函数拟合误差ε对支持向量机学习能力影响不大，因此，可以不作为主要因素考虑^[15]。

3  蛙跳算法改进支持向量机模型(SFLA-SVM)

蛙跳算法用于优化支持向量机的关键参数(c和σ)，每一个青蛙所处的位置向量对应一组特定的关键参数组合，对其位置适应度的评价函数可以定义为：

            (3)

其中：N为训练样本数量；和Y_i分别为训练预测值和真实值。

通过蛙跳算法不重种群青蛙之间全局信息和局部搜索之间的信息交换以及迭代实现最优搜索，最优个体的位置向量即对应最佳的关键参数组合。输出最佳参数组合作为支持向量机预测模型的核函数关键参数。具体的算法运行过程如图1所示。

图1  蛙跳算法优化SVM关键参数示意图

Fig.1  Schemes of SVM key parameters optimization by SFLA

4  模型应用实例

4.1  实证环境

以1979—2000年中国能源总消费的历史数据作为训练样本，以2001—2009年的能源消费量作为检验样本，运用本文设计的预测方法进行实证研究，以检验本文设计算法对于预测效果的改进情况。本文实证研究的物理平台为：PC终端，CPU为Intel 酷睿i7 2600 (6核)，内存为4 G，WINOWS732位操作系统，MATLAB7.1运行环境。用本文提出的SFLA-SVM分别与PSO-SVM和SVM模型进行比较。

4.2  实证结果分析

对比SFLA-SVM和PSO-SVM的训练过程，如图2所示。从图2可见：SFLA-SVM和PSO-SVM方法在同一适应度评价函数下，SFLA-SVM的训练过程曲线比较平滑，算法收敛速度较慢，但最终效果比PSO- SVM的好。说明与PSO-SVM算法相比，SFLA-SVM算法运行的全局性、鲁棒性更好，可更好地发挥对SVM的优化作用。

分别将SFLA-SVM，PSO-SVM和SVM的能源需求预测值与2000—2009年相应的真实值进行比较，结果见图3。从图3可以发现：总体来说，2004年以前各自的能源需求精度要高于2009年以后的精度，但总体趋势比较吻合；随着预测时序的延伸，误差增大。SFLA-SVM的预测曲线比PSO-SVM和SVM的预测曲线更加贴近真实曲线，说明SFLA-SVM模型的能源需求预测效果要比PSO-SVM和SVM的好。

图2  SFLA改进SVM训练过程算法SFLA-SVM与PSO-SVM算法对比

Fig.2  Comparison of train process of SFLA-SVM and PSO-SVM

图3  蛙跳算法改进支持向量机预测结果

Fig.3  Comparison of results between improved SVM and other SVM

综合比较SFLA-SVM，PSO-SVM和SVM的平均精度和运行时间，如表1所示。从表1可见：蛙跳算法改进支持向量机SFLA-SVM比PSO-SVM和SVM的精度有明显提高，增加的运行时间很少，分别仅为51 s和109 s。这表明SFLA-SVM算法提高了SVM预测模型的预测精度，而造成的效率损失不显著，在可接受范围之内。

表1  SFLA-SVM综合预测效果对比分析

Table 1  Comprehensive analysis on forecasting results of SFLA-SVM

5  结论

(1) 本文提出的蛙跳算法能够有效地进行支持向量机关键参数的优化，避免支持向量机产生“过学习”或“欠学习”等问题，从而使得支持向量机能够获得更强的学习能力。

(2) 中长期能源需求问题受多种复杂因素的影响，尤其是宏观经济和产业政策的影响，要更加准确地预测分析中长期能源需求变化趋势，需要对表征宏观经济和产业政策的影响因子进行深入研究，以构建更贴近实际情况的量化分析模型。

(3) 对本文提出的算法和预测分析模型，还可通过改进支持向量机学习方法和预测模型进行改进，以便得到更加精确的预测模型。

参考文献：

[1] 牛东晓, 营树华, 赵磊, 等. 电力负荷预测技术及其应用[M]. 北京: 中国电力出版社, 2002: 15-29.
NIU Dong-xiao, YING Shu-hua, ZHAO Lei, et al. Electric power load forecasting technology and its application[M]. Beijing: China Electric Power Press, 2002: 15-29.

[2] 靳忠伟, 陈康民, 闰伟, 等. 基于支持向量机的中长期电力负荷预测研究与应用[J]. 上海理工大学学报, 2008(2): 31-34.
JIN Zhong-wei, CHEN Kang-min, YAN Wei, et al. Study and application of support vector machine to forecast mid-long-term electric power load[J]. Journal of University of Shanghai for Science and Technology, 2008(2): 31-34.

[3] 孙翠娟. 基于K型核函数的支持向量机[J]. 淮海工学院学报: 自然科学版, 2006, 15(4): 4-7.
SUN Cui-juan. Support vector machine based K-type kernel function[J]. Journal of Huaihai Institute of Technology: Natural Sciences Edition, 2006, 15(4): 4-7.

[4] Eusuff M M, Lansey K E. Optimization of water distribution network design using the shuffled frog leaping algorithm[J]. Journal of Water Sources Planning and Management, 2003, 129(3): 210-215.

[5] 韩毅, 蔡建湖, 周根贵, 等. 随机蛙跳算法的研究进展[J]. 计算机科学, 2010, 37(7): 16-19.
HAN Yi, CAI Jian-hu, ZHOU Gen-gui, et al. Advances in shuffled frog leaping algorithm[J]. Computer Science, 2010, 37(7): 16-19.

[6] 李英海, 周建中, 杨俊杰, 等. 一种基于阈值选择策略的改进混合蛙跳算法[J]. 计算机工程与应用, 2007, 43(35): 9-21
LI Ying-hai, ZHOU Jian-zhong, YANG Jun-jie, et al. Modified shuffled frog leaping algorithm based on threshold selection strategy[J]. Computer Engineer and Application, 2007, 43(35): 9-21.

[7] 熊伟平, 曾碧卿. 几种仿生优化算法的比较研究[J]. 计算机技术与发展, 2010, 10(3): 9-12.
XIONG Wei-ping, ZENG Bi-qing. Studies on some bionic optimization algorithm[J]. Computer Technology and Development, 2010, 10(3): 9-12.

[8] Elbeltagi E, Hegazy T, Grierson D. Comparison among five evolutionary-based optimization algorithms[J]. Advanced Engineering Informatics, 2005, 19(1): 43-53.

[9] Rahimi-Vahed A, Dang C M, Rafiei H. A novel hybrid multi-objective shuffled frog-leaping algorithm for a bi-criteria permutation flow shop scheduling problem[J]. International Journal of Advanced Manufacturing Technology, 2009, 41(11): 1227-1239.

[10] YANG Cheng-san, CHUANG Li-ye, KE Chao-huan, et a1. A combination of shuffled frog-leaping algorithm and genetic algorithm for gene selection[J]. Journal of Advanced Computational Intelligence and Intelligent Informatics, 2008, 12(3): 218-226.

[11] Lin S W, Ying K C, Chen S C, et al. Particle swarm optimization for parameter determination and feature selection of support vector machines[J]. Expert Systems with Applications, 2008, 35(4): 1817-1824.

[12] 伍铁斌, 成运, 周桃云, 等. 基于混沌遗传算法的PID参数优化[J]. 计算机仿真, 2009, 26(5): 202-205.
WU Tie-bin, CHENG Yun, ZHOU Tao-yun, et al. Optimization control of PID based on chaos genetic algorithm[J]. Computer Simulation, 2009, 26(5): 202-205.

[13] 付阳, 李昆仑. 支持向量机模型参数选择方法综述[J]. 电脑知识与技术, 2010, 6(10): 8081-8082.
FU Yang, LI Qun-lun. A survey of model parameters selection method for support vector machines[J]. Computer Knowledge and Technology, 2010, 6(10): 8081-8082.

[14] Huang C L, Wang C J. A GA-based feature selection and parameters optimization for support vector machines[J]. Expert Systems with Applications, 2006, 31(2): 230-231.

[15] 朱凤明, 樊明龙. 混沌粒子群算法对支持向量机模型参数的优化[J]. 计算机仿真, 2010, 27(11): 183-186.
ZHU Feng-ming, FAN Ming-long. Chaos particle swarm optimization algorithm for optimizing the parameter of SVM[J]. Computer Simulation, 2010, 27(11): 183-186.

(编辑 陈灿华)

收稿日期：2010-09-28；修回日期：2010-12-16

基金项目：国家自然科学基金资助项目(70901025)

通信作者：宋晓华(1971-)，男，黑龙江五常人，从事技术经济评价理论与方法、负荷预测方法与技术等研究；电话：18911091017；E-mail: sxhbj2011@126.com