Finite element analysis of stiffness and static dent resistance of aluminum alloy double-curved panel in viscous pressure forming

LI Yi(李 毅), WANG Zhong-Jin(王忠金)

School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China

Received 10 June 2009; accepted 15 August 2009

Abstract: The static dent resistance performance of the aluminum alloy double-curved panel formed using viscous pressure forming (VPF) was studied by finite element analysis, which mainly considers the forming process conditions. The whole simulation consisting of three stages, i.e., forming, spring-back and static dent resistance, was carried out continuously using the finite element code ANSYS. The influence of blank holder pressure (BHP) and the drawbead on the stiffness and the static dent resistance of the panels formed using VPF was analyzed. The results show that the adequate setting of the drawbead can increase the plastic deformation of the double-curved panel, which is beneficial to the initial stiffness and the static dent resistance. There is an optimum BHP range for the stiffness and the static dent resistance.

Keywords: aluminum alloy; double-curved panel; viscous pressure forming; panel stiffness; static dent resistance; finite element analysis

1 Introduction

There is a great concern about the mass reduction of vehicles. So some new materials, such as aluminum alloy, are continuing to increase in the automotive industry. The use of new materials has led to greater focus on the stiffness and dent resistance of automotive panels.

Phenomena associated with denting can be divided into two categories: depending on the elastic or inelastic nature of the response. During the elastic deformation, the panel denting will disappear after unloading. The panel stiffness is defined as the resistance of a panel to elastic deformation. Dent resistance is mainly referred to as static or dynamic dent resistance. The static dent resistance is a measure of the panel resistance to permanent deformation caused by static forces. The dynamic dent resistance is associated with dynamic loads[1]. This study mainly deals with the static dent resistance and stiffness.

Many studies regarding the dent resistance and stiffness of automotive panels were carried out. ASNAFI[2] analyzed the stiffness and dent resistance of double-curved car body panels theoretically and experimentally. Results showed that the stiffness and dent resistance of the double-curved panels could be predicted by the principal surface strains and the panel radii at the panel centre. In order to set the criterion of panel stiffness, ZHAO et al[3] used automatic testing device to obtain the load—deflection curves of the shallow shell parts, for different materials, different radii, different arc heights and different thicknesses. HOLMBERG and THILDERKVIST[4] investigated the influence of material properties and stamping process conditions on the stiffness and static dent resistance of automotive panels. It was found that increasing blank holding force with consequently increasing strain levels in the panels is generally beneficial to the static dent resistance. The initial stiffness of panels stamped with the low blank holding force condition was slightly higher than that of the panels with high blank holding force. The influence of different punches and boundary conditions on the dent resistance performance of the aluminum alloy double-curved panel was investigated by EKSTRAND and ASNAFI[5]. It was found that it was essential that the panel size and shape, the site of measurement, the boundary condition and the shape of the testing punch were selected to obtain a reasonable standard for stiffness and dent resistance tests. Based on the shallow shell theory, ZHANG et al[6] obtained the expression of dent resistance stiffness of double-curved shallow shell under the concentrated load condition.

Viscous pressure forming (VPF) uses a semi-solid, flowable, highly viscous and strain rate sensitive macromolecule polymer (viscous medium) as the flexible-punch. Because of high viscosity and strain rate sensitivity of the viscous medium, VPF improves the formability of the sheet[7-10] and is suitable to form complex shape parts or difficult-to-form sheet metal[11-14]. Viscous pressure forming technology was used to product aluminum alloy panels in previous studies[15]. However, studies on the dent resistance of aluminum alloy panels formed by VPF have not yet reported. In this work, the stiffness and static dent resistance of the aluminum alloy double-curved panel formed by VPF were analyzed by finite element method (FEM). The main objective is to investigate the influence of process conditions on the stiffness and static dent resistance of automotive panels.

2 Finite element analysis model

2.1 VPF principle

The principle of VPF technology is shown in Fig.1. The medium chamber is filled with the viscous medium before forming panels. The sheet blank is placed on the medium chamber, and then appropriate blank holding pressure (BHP) is imposed by the die. BHP not only needs to make the blank flow sufficiently, but also ensures that the medium does not leak. The pistons push the viscous medium upwards and pressure is generated within the medium. The panel is subsequently formed under the pressure.

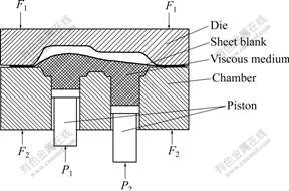
Fig.1 Principle of VPF technology

2.2 Principle of static dent resistance test

The principle of the static dent resistance test is shown in Fig.2. The panel is first fixed appropriately at the table, and then slowly loaded up to a certain force level and unloaded thereafter. The load is applied using a hemispherical punch of a certain diameter. The force and deflection are measured continuously during loading and unloading. The permanent dent depth of the panel is then measured after unloading. The static dent resistance is defined as the required maximal force for a certain residual dent depth. Normally, this procedure is repeated at different load levels to obtain the relation between the applied load and the dent depth. The stiffness can be defined as the initial slope of the force—deflection curve. The testing is also carried out at several different locations of the panel since the dent resistance varies from point to point. In this investigation, the attention is paid solely to the dent resistance at the panel centre.

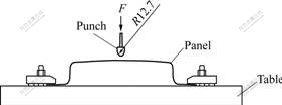
Fig.2 Principle of static dent resistance test

2.3 Finite element modeling

Since the exterior body panels for automobiles often feature curves in one or more directions, the double-curved panel is selected to simulate a curved exterior body panel. The double-curved panel shape is shown in Fig.3. One quarter of the geometry is selected and modeled by taking advantage of symmetry to reduce computational expense. Finite element model for the VPF process is shown in Fig.4. The die and the sheet blank are modeled using four-node quadrilateral and Belytschko-Tsay shell element. The viscous medium is modeled using eight-node hexahedron body element. Finite element model for the dent resistance is shown in Fig.5. The panel flange is entirely constrained during the dent resistance simulation. The whole analysis process consists of three stages, i.e. forming, spring-back and dent resistance analysis. Three stages are simulated continuously using the finite element code ANSYS. The

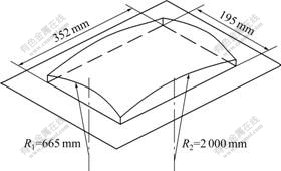
Fig.3 Geometry of double-curved panel

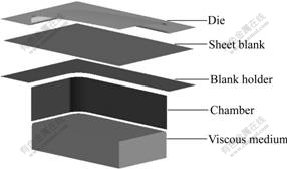
Fig.4 FE model of VPF process

Fig.5 FE model for dent resistance simulation

VPF process simulation is carried out using dynamic explicit algorithm. Static implicit algorithm is used for the spring-back and the dent resistance.

2.4 Materials

The aluminum alloy sheet used in finite element analysis is 6k21-T4 with a thickness of 1.2 mm. Its chemical composition and material properties are listed in Tables 1 and 2, respectively. The viscous medium is methyl vinyl silicone rubber. The flow stress—strain rate curve of the viscous medium is shown in Fig.6.

Table 1 Chemical composition of 6k21-T4 aluminum alloy sheet (mass fraction, %)

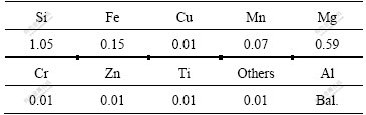
Table 2 Material properties of 6k21-T4 aluminum alloy sheet

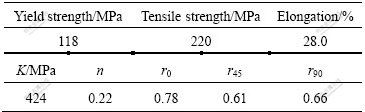
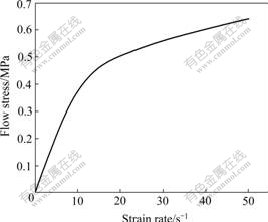
Fig.6 Flow stress—strain rate curve of viscous medium

3 Results and discussion

3.1 Effect of BHP on stiffness and static dent resistance

The forming conditions, such as BHP, influence the dent resistance performance of the double-curved panel, so the dent resistance performance with four blankholding conditions (BHP=1, 3, 6 and 9 MPa) is analyzed. The thickness reduction distributions of panels along the X-axis and the Y-axis are shown in Fig.7. The thinning region mainly focuses on the corner of the double-curved panel. In addition, the thickness distribution of the panel centre is even for every blankholding condition.

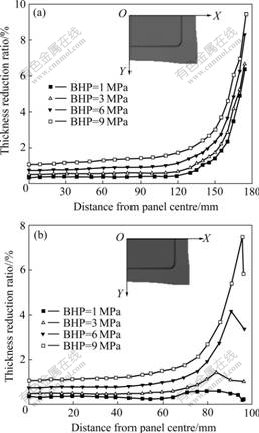
Fig.7 Effect of BHP on thickness reduction of panels along X-axis(a) and Y-axis(b)

The force—deflection curves of the panels under different blankholding conditions are shown in Fig.8. There are obvious differences between the curves. The maximum force and the final dent depth obtained using finite element simulations are shown in Fig.9. It can be found that the required load to cause a plastic deformation of a certain depth for the high BHP is higher than that for the low case. The stiffness is given by the initial slope of the force—deflection curve, as shown in Fig.10. With four blankholding conditions, the maximum stiffness is obtained when BHP is 6 MPa and the minimum stiffness appears when BHP is 1 MPa. The initial stiffness of the double-curved panel mainly depends on the sheet thickness, the panel radius and the elastic modulus. With BHP increasing, the thickness reduction increases, resulting in the stiffness reduction. With the plastic deformation increasing, however, the spring-back of the panel decreases, resulting in the reduction of the panel radius, which is beneficial to improving the stiffness. Therefore, the synthetic effect of the sheet thickness and the spring-back on the stiffness produces a complex result. When BHP is lower, the spring-back plays the main role and the stiffness increases with increasing BHP; but when BHP is up to a certain value, the influence of the thickness reduction is greater than that of the spring-back and the stiffness decreases with increasing BHP.

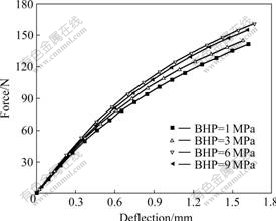
Fig.8 Force—deflection curves under different blankholding conditions

Fig.9 Force—dent depth curves under different blankholding conditions

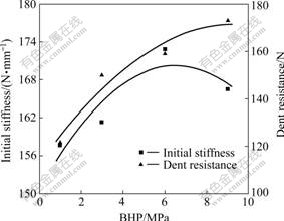
Fig.10 Effect of BHP on stiffness and static dent resistance

Fig.10 also shows the required maximum force to cause the dent depth of 0.1 mm, which is generally accepted as the lower threshold of a visible dent. The required maximum force is usually a means to measure the static dent resistance of a panel. The corresponding values are interpolated from the force—dent depth curves (Fig.9) by a least-squares fitting of a linear function. The panels with BHP of 3, 6 and 9 MPa show the dent resistance approximately 23.2%, 30.5% and 42.0% higher than the panel with BHP of 1 MPa, respectively. This shows that increasing BHP results in the increase of dent resistance within the BHP range of this study. The reason can be related to the better work hardening. Increasing BHP, with consequently increasing plastic deformation in the panels, results in the better work-hardening of the material. This work-hardening means that the yield stress is increased for subsequent loading. The influence of the yield stress is greater than that of the thickness reduction and then the dent resistance increases. Moreover, increasing plastic deformation results in the smaller spring-back, which is also beneficial to improving the static dent resistance of the double-curved panel.

According to the above analysis, the effect of BHP on the stiffness and static dent resistance should be synthetically considered and optimized to obtain the panel with the ideal stiffness and dent resistance. Although the panel with BHP of 6 MPa shows the maximum initial stiffness, the panel with BHP of 9 MPa shows the maximum dent resistance within the selected BHP range. Thereby, the optimum BHP should be between 6 and 9 MPa.

3.2 Effect of drawbeads on stiffness and static dent resistance

The setting of the drawbead is an effective technique to improve the formability of the double- curved panel. The effect of the drawbead height (H) on the stiffness and static dent resistance is also analyzed. The panel with H of 2 mm is formed when BHP is    1.0 MPa. The force—deflection curves at different drawbead heights are given in Fig.11. The required load to cause a certain deflection for the drawbead height of 2 mm is higher than that of the no drawbead case. And the larger the deflection, the more obvious the difference. The force—dent depth curves for both cases are shown in Fig.12. The curve with the drawbead height of 2 mm is higher than that of the no drawbead case.

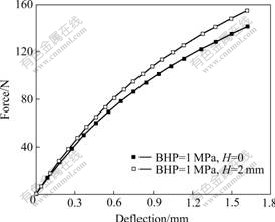
Fig.11 Effect of drawbead on force—deflection curve

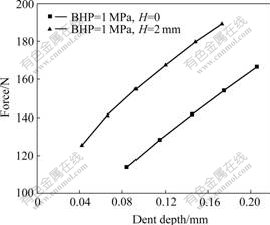
Fig.12 Effect of drawbead on force—dent depth curve

The initial stiffness values for both cases are given in Table 3. The panel with the drawbead height of 2 mm shows the stiffness approximately 5.5% higher than the panel with no drawbead. For both cases, the thickness reduction is almost the same at the panel centre. The thickness reduction of the former is larger than that of the later in the other area of panel. Increasing plastic deformation reduces the spring-back of the panel. The influence of the spring-back is greater than that of the thickness reduction. And the panel with the drawbead shows the higher stiffness.

Table 3 Stiffness and dent resistance of panels at different drawbeads

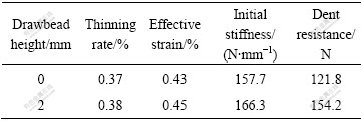
Table 3 also lists the dent resistance at different drawbeads. These values are interpolated from the force—dent depth curves (Fig.12) by a least-squares fitting of a linear function. The panel with the drawbead height of 2 mm shows that the dent resistance is approximately 26.6% higher than that of the panel with no drawbead. The drawbead restrains the flow of the material to increase the plastic deformation of the panel. Thereby, increasing plastic deformation results in better work-hardening of the material. The influence of the work-hardening is greater than that of the thickness reduction, so the dent resistance increases. Otherwise, the setting of the drawbead results in decreasing spring- back and improves the static dent resistance of the panel.

4 Conclusions

1) The blankholding condition affects the formability of the aluminum alloy double-curved panel in VPF. The thickness reduction and the plastic deformation of the panel are increased by controlling BHP and drawbead height. Under different blankholding conditions, the thickness distribution is even at the panel centre.

2) The initial stiffness of the double-curved panel is influenced by the blankholding condition. When BHP ＜6 MPa, the stiffness increases with increasing BHP; but when BHP ＞6 MPa, the stiffness decreases with increasing BHP. In addition, the reasonable setting of the drawbead can improve the initial stiffness of the double-curved panel.

3) The forming condition also affects the static dent resistance of the double-curved panel. Within a certain BHP range, increasing BHP can increase the plastic deformation of the panel and is beneficial to improving the static dent resistance. The appropriate setting of the drawbead can also improve the static dent resistance.

References

[1] HOLMBERG S, NEJABAT B. Numerical assessment of stiffness and dent properties of automotive exterior panels[J]. Mater Des, 2004, 25: 361-368.

[2] ASNAFI N. On strength, stiffness and dent resistance of car body panels[J]. J Mater Proc Technol, 1995, 49: 13-31.

[3] ZHAO Li-hong, YANG Yu-ying, SUN Zhen-zhong. Study on evaluation criterion of auto-body panels stiffness[J]. Mater Sci Technol, 2004, 12(4): 425-428.

[4] HOLMBERG S, THILDERKVIST P. Influence of material properties and stamping conditions on the stiffness and static dent resistance of automotive panels[J]. Mater Des, 2002, 23:681-691.

[5] EKSTRAND G, ASNAFI N. On testing of the stiffness and the dent resistance of autobody panels[J]. Mater Des, 1998, 19: 145-156.

[6] ZHANG Yan, LAI Xin-min, ZHOU Ping, WANG Wu-rong. Lightweight design of automobile component using high strength steel based on dent resistance[J]. Mater Des, 2006, 27: 64-68.

[7] LIU Jian-guang, WANG Zhong-jin, WANG Zhong-ren. Numerical simulation of the influence of viscous adhesive stress on the viscous pressure bulging process of hemispherical sphere[J]. Trans Nonferrous Met Soc China, 2003, 13(6): 1354-1359.

[8] LIU Jian-guang, WANG Zhong-jin, GAO Tie-jun. Experimental study on effect factors of viscous adhesive stress in viscous pressure forming[J]. Chin J Mech Eng, 2006, 42(10): 146-150.

[9] AHMETOGLU M, HUA J, KULUKURU S, ALTAN T. Hydroforming of sheet metal using a viscous pressure medium[J]. J Mater Proc Technol, 2004, 146: 97-107.

[10] GUTSCHER G, WU H C, NGAILE G, ALTAN T. Determination of flow stress for sheet metal forming using the viscous pressure bugle (VPB) test [J]. J Mater Proc Technol, 2004, 146: 1-7.

[11] LIU J H, WESTHOFF B, AHMETOGLU M A, ALTAN T. Application of viscous pressure forming (VPF) to low volume stamping of difficult-to-form alloys-results of preliminary FEM simulations[J]. J Mater Proc Technol, 1996, 53: 49-58.

[12] WANG Zhong-jin, WANG Xin-yun, WANG Zhong-ren. Viscous pressure forming (VPF) of corrugated thin-walled sheet part with small radius[J]. J Mater Proc Technol, 2004, 145: 345-35.

[13] SHULKINA L B, POSTERAROB R A, AHMETOGLU M A, KINZEL G L, ALTAN T. Blank holder force (BHF) control in viscous pressure forming (VPF) of sheet metal[J]. J Mater Proc Technol, 2000, 98: 7-16.

[14] WANG Zhong-jin, LIU Jian-guang, WANG Xin-yun, et al. Viscous pressure forming (VPF): State-of-the-art and future trends[J]. J Mater Proc Technol, 2004, 151: 80-87.

[15] WANG Zhong-jin, LI Yi. Formability of 6k21-T4 car panel sheet for viscoelastic-plastic flexible-die forming[J]. J Mater Proc Technol, 2008, 201: 408-412.

(edited by CHEN Wei-ping)

Corresponding author: WANG Zhong-jin; Tel: +86-451-86418643; E-mail: wangzj@hit.edu.cn