基于极大代数法的铝板轧制系统鲁棒性能
胡 扬，桂卫华，叶华文，侯文明
(中南大学 信息科学与工程学院，湖南 长沙，410083)
摘 要：为了优化铝板轧制的时间，提高系统的鲁棒性，以极大代数法和排队论为工具，对铝板多队列轧制系统进行分析。根据轧机与工件之间的工艺路径规则和加工条件规则，以极大代数法为理论依据建立轧制控制系统的闭环控制模型，对极大代数法的运算特性进行分析；构造轧制过程的多队列多服务器模型；定义多队列系统中参数摄动和鲁棒性的概念；用基于极大代数法的串行生产线的闭环线性模型来研究采用不同的铝板轧制队列对系统稳态周期性能的影响；以轧制过程的最短生产周期为优化目标，运用摄动分析对系统的多个调度队列的性能进行比较讨论，从而通过周期配置得到铝板轧制的优化调度方案。分析结果表明：基于极大代数法的系统分析能有效地对调度队列的摄动性进行比较，从而改善了轧制系统的鲁棒性，缩短了系统总运行时间，提高了运行效率。
关键词：极大代数法；离散事件动态系统；鲁棒性；摄动分析；优化调度
中图分类号：TP15；TF355 文献标识码：A 文章编号：1672-7207(2009)03-0742-07
Robustness performance of aluminum plate rolling system based on maximum algebra method
HU Yang, GUI Wei-hua, YE Hua-wen, HOU Wen-ming
(School of Information Science and Engineering, Central South University, Changsha 410083, China)
Abstract: In order to decrease aluminum plate rolling time and enhance system robustness, the aluminum plate rolling multi-queue system was analyzed by max algebra theory and queue theory. Based on the technologic route rules and process condition rules between machine tools and work pieces, a rolling control system closed-loop model was built up by max algebra and the computing character of maximum algebra was introduced. Moreover, multi-server/ multi-queue system model for rolling process was built. The concepts of parameter perturbation and robustness were defined. The influence of system stable cycle in different kinds of aluminum plates rolling queues was studied by the product lines closed-loop model. Taking the minimum production period as the optimal object, perturbation analysis was made to evaluate the different queues performances. The results show that the optimal scheduling plan can be obtained on the basis of period assignment method. The perturbation performance in scheduled queues can be compared by maximum algebra theory. The system robustness is improved and the total system running time is decreased. The system efficiency is improved by the scheduling method.
Key words: maximum-algebra; discrete event dynamic system; robustness; perturbation analysis; optimal scheduling
铝板轧制生产线是一类典型的离散事件动态系统。关于离散事件动态系统的分析方法有自动机、Petri网、排队论、极大代数等。自动机方法基于“开关电路”的思想，通过控制电路开关来调节系统状态的转变。该方法的思想较为直观，但具体实现却依赖于电路的硬件组成，系统复杂度较高[1-3]。Petri网是试图通过图论的方法来解决离散事件状态转换问题的较好途径。近年来，在普通Petri网的基础上不断衍生出新的分支，如时间Petri网、有色Petri网。这些都是对Petri网方法的完善。但Petri网的缺点是随着系统中回路的增多，Petri网的复杂度也呈几何级数上升，且该方法难以与目前较为成熟的现代控制理论相联系[4-5]。排队论是纯粹按照队列/服务器模型进行分析的方法，其服务时间与事件启动时间服从一定统计规律。该方法是分析离散事件动态系统的经典方法，但随着队列数目的增多，运算复杂度也大大提高[6-9]。
极大代数法结合了排队论模型的完备性和现代控制理论中矩阵分析的便利性。通过极大代数中的特殊运算规则，可把逻辑非线性关系转化为极大代数意义下的线性关系，为对离散事件动态系统(DEDS)建立形式简单的代数层次线性模型和定量分析DEDS演化过程的规律开辟了一条可行的途径[10-11]。
1 铝板轧制工艺过程模型与参数
1.1 铝板轧制工艺
铝板加工总体流程包括：铣面、表面处理、加热、热轧、粗轧、精轧、退火、表面清洗、检验、包装入库。其中，粗轧和精轧属于冷轧环节，本文所要研究的铝板轧制流程包括热轧和冷轧。
铝板轧制流水线是属于多队列多服务器的排队模型，这里选取3种不同轧制要求的板坯P1，P2和P3建立排队模型，如图1所示[12-14]。
图1 铝板轧制排队模型
Fig.1 Aluminum plate rolling queue model
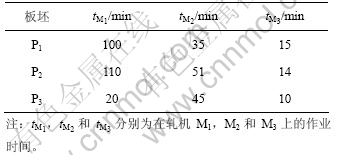
各种轧机出口厚度控制参数如表1所示，铝板各轧制工序的作业时间如表2所示，板坯P1，P2和P3初始厚度分别为25，30和35 mm。
表1 各轧制工序出口厚度
Table 1 Rolling activities exit gauge in mills
表2 铝板各轧制工序的作业时间
Table 2 Rolling activities working time
1.2 轧制过程建模
1.2.1 串行生产线的代数层次模型
设串行生产线的轧制缓冲区为无限大。基于实际串行生产线加工过程，有如下2个基本假设[15-16]。
假设1 每类工件在机床的加工路径和每台机床对工件的作业时间被确认为是确定的，不考虑可能导致其变动的各种随机性因素，加工过程是一个确定性过程。
假设2 每台机床前的缓冲区中工件队列的长度不受限制，不需要考虑系统中的阻塞问题。
对于串行生产线，其加工过程可以用n台机床M1，M2，M3，…，Mn对m种工件P1，P2，P3，…，Pm的顺序加工的过程来表征。按照加工工艺路径的规定，每种工件都要依次经过n台机床设备进行加工，而每台机床都要对m种工件依次加工。串行生产线的加工过程可以是单个批次性的，也可以是多个批次性的。对于多个批次性的加工过程，所属的批次用k来表示，其中k=1, 2, …。
在系统变量(状态，输入，输出)与系统资源(机床与工件)之间建立对应关系。
a. 状态变量：对所讨论的串行生产线，xij为状态变量，定义为：xij是相对于一个批次加工中，机床Mj对工件Pi加工活动的最早开始时间。其中，i=1, 2, …, n; i=1, 2, …, m。
b. 输入变量：对所讨论的串行生产线，Ua为输入变量，定义为：Ua是相对于一个批次加工中，第a个资源投入其第1个加工活动的开始时间。其中，a=1, 2, …, n+m。资源的序号按先机床后工件进行排序。
c. 输出变量：对所讨论的串行生产线，Ya为输出变量，定义为：Ya是相对于一个批次加工中，第a个资源从加工过程中完全释放的最早时间。其中，a=1, 2, …, n+m。资源的序号按先机床后工件进行排序。
定义加工时间：对所讨论的串行生产线，以tij表示加工时间，即tij是相对于一个批次加工中，机床Mj对工件Pi加工的作业时间与工件Pi由机床Mj传送至下一机床Mj+1的传输时间之和。
1.2.2 基于极大代数法的串行生产线建模
根据加工时间定义，时间矩阵T为：
。
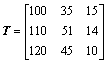系统的开环状态矩阵为：
。
其中：符号“.”表示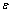
(下同)。
输入矩阵为：
。
输出矩阵为：
。
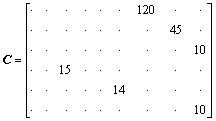铝板轧制系统的开环线性模型为基于上述各实数矩阵A，B和C的形式[17-19]：
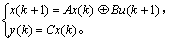(1)
2 轧制系统的摄动分析
2.1 系统参数摄动与系统鲁棒性定义
系统模型的系统矩阵元素的摄动，将导致系统性能如周期性稳态参量的变化。对任意1个矩阵T, tij为矩阵T的各个元素，T*为T矩阵内各个元素摄动后的摄动矩阵，(tij)*为矩阵T*的各个元素。则矩阵T*的摄动量规定为如下定义的1个标量：
若λ和λ*分别为标称系统和其摄动系统在极大代数上的特征值，则由参数摄动所导致的系统特征值的摄动量定义为：
对串行生产线一类的离散事件动态系统，λ是系统周期性稳态的主要性能参量。当系统各个参数矩阵A，B和C的元素偏离标称值而出现摄动时，可以定量分析和估计由于参数摄动所引起的稳态性能参量λ的改变量[20-21]。
鲁棒性是对一切实用系统的基本要求，直观地说，鲁棒性是指系统某个性能相对于系统参数摄动的不敏感性。在铝板轧制系统中，由于系统的内部和外部的因素，参数的摄动是不可避免的。
对任一标称系统矩阵M=(mij)，mij称为标称元，若(mij)*为相应的摄动元，则元mij的摄动量定义为：
若λ完全不受mij有界摄动的影响, 即对mij到(mij)*的任意有界摄动总保持λ=λ*成立，则称稳态参量λ相对于系统矩阵的元素mij是鲁棒的。鲁棒性准则选取函数为：
若RF(mij)=0，则λ对于mij为鲁棒的；若RF(mij)≠0，则λ对于mij为非鲁棒的。并且函数RF(mij)越大，摄动对稳态参量λ的影响越大。
若可摄动元(不为ε的元素)mij的允许摄动范围定义为围绕标称值mij的1个最大闭区间
，则对于所有可能的摄动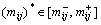
，λ均是鲁棒的，即RF(mij)≡0成立。
鲁棒性的度量为稳态参量特征值λ相对于可摄动元mij的鲁棒性度量，定义鲁棒性的度量如下：
鲁棒性度量RM(mij)越大，对应的稳态参量λ对可摄动元mij的鲁棒性程度越高。
2.2 铝板轧制系统闭环模型
串行生产线这一类的离散事件动态系统性能指标的优化，就是在一定类型的系统输入排列中找到周期稳态输出的最小特征值λ*，即求解λ*=min(λ1，λ1，…，λi)，并且运用极大代数法求出在最小特征值下所对应的各项系统演化的性能指标如：，RF(mij)，RM(mij)。
如上所述，对于铝板轧制控制系统，其优化调度就是要找到一个最合适的铝板排队队列，使系统稳态运行的周期最短，即在待轧铝板的排队种类中找到周期稳态输出的最小特征值λ*，并且运用极大代数法计算分析系统的各项性能指标[22]。
要对系统的闭环线性模型进行推导和分析，首先要确定系统的闭环参数矩阵M，根据反馈常数矩阵的意义，反馈矩阵中元素ki表示第i个资源从第k-1批加工过程的释放时刻到第k批加工过程的最早投入时刻之间的时间间隔，基于开环参数矩阵的结果，并考虑到此处
，根据所计算的开环系统模型的各个矩阵值，可以确定出系统的闭环参数矩阵M为：
。
因此，铝板轧制系统的闭环模型为基于上述闭环实参数矩阵M的线性形式：
；k=2, 3, …。 (7)
2.3 排队系统摄动分析
设铝板轧制的初始输入为u(1)=(0, 100, 120, 0, 0, 20)T，顺序是先轧机后铝板，为了运算方便，数据尽量取整。则系统输出的演化过程经递推得出：
。 (8)
运用式(16)中所示的迭代算法，由初始输入u(1)，可以定出初始输出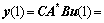
(625, 670, 635, 525, 570, 635)T递推求出系统输出，如表3所示。
表3 系统输出仿真结果
Table 3 System output simulation results
已知铝板轧制串行生产线中轧制的铝板P1的厚度为25 mm，P2的厚度为30 mm，P3的厚度为35 mm，在按先轧制P1，再轧制P2，后轧制P3的排列情况下得到表3中的各输出演化结果，从表3中可以得出系统的特征值λ=605 min。该值代表在铝板轧制排队队列为P1P2P3的情况下，系统输出变量中各变量随系统演化的时间间隔，也就是这批铝板轧制的生产周期。由于3种铝板共有6种排队类别，改变铝板的排列而且相应改变系统的矩阵参数，再重复5次仿真计算，结果如表4所示。
表4 不同铝板队列的仿真结果
Table 4 Simulation results for different Al plate queues
从表4可以看出，在排列为P2P3P1和P3P2P1时得到轧制周期最小值均为λmin=595 min，显然，有2种轧制队列P2P3P1和P3P2P1在“生产周期最小”这一个优化性能指标上符合调度要求。
与生产周期λmin=595 min的2种排队方式P2P3P1和P3P2P1相应的时间矩阵为：
；
。
给予这2个时间矩阵各铝板轧制位置相同的元素等量的增量摄动，选定摄动后的矩阵为：
；
。
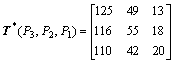可见，加工时间矩阵T的摄动量：
；
，
；
，
。
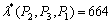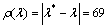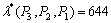显然，排列P3P2P1的摄动量ρ(λ)=49，比排列P2P3P1的摄动量ρ(λ)=69小，这说明排列P3P2P1的鲁棒性强，因此，排列P3P2P1为最优队列。
3 系统性能鲁棒性分析
在排列P3P2P1的基础上计算其鲁棒性函数RF(mij)，进一步对此队列进行性能分析。
生产周期λ=595 min，排列为P3P2P1的情况下的闭环系统参数矩阵为：
。
为了保证铝板轧制的质量以及安全性，对矩阵M中各元素随机取一定范围(摄动量在50左右)内的增性摄动，对系统摄动进行初步分析，有摄动矩阵：
。
可得：
。
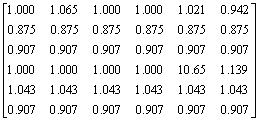该参数矩阵的计算结果可以说明系统轧制时间矩阵摄动前后的系统矩阵M中的对应元素受影响的程度。计算结果表明，闭环参数矩阵M的各标称元在上述增性摄动情况下的结果是RF(mij)都不为零，显然λ对于各mij都是非鲁棒的。所以，在此采用的服务时间增性摄动量已经超出系统鲁棒性能范围。这里需要进一步计算系统保持鲁棒性能时系统矩阵M中所有可摄动元的允许摄动范围及各位置元素的鲁棒性度量[23]。
单摄动元增性摄动鲁棒性判据： 对所讨论的一类离散事件动态系统，设
为
的不可简约系统矩阵M的唯一可摄动元，且摄动为增性的。定义mij增性摄动的上界值m+ij为：
(9)
当且仅当mij增性摄动值
?[mij，
]，系统稳态参量(即特征值)λ对于元mij的增性摄动是鲁棒的，即有鲁棒性函数RF(mij)=0。
根据式(9)，对于i=j型可摄动元，确定其允许增性摄动范围，以使系统的稳态参量(即特征值)λ保持不变为目标，此处λ=595，可以定出，对角元型可摄动元的增性摄动范围?[mij，]为：
，
，
，
，
，
。
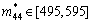对于i?j型可摄动元，确定其允许增性摄动范围。可以先通过计算机计算定出幂矩阵MK(k=2, 3, 4, 5)，再根据式(9)对各个可摄动元定出其允许摄动上限的值，进而得出其允许增性摄动范围?[mij，]，为：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
。
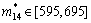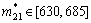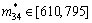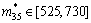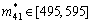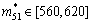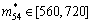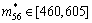当系统矩阵M中非ε可摄动元mij的同时，增性摄动限于在各自的允许范围?[mij，]时，可使系统稳态参量(即特征值)λ保持不变，也就是稳态参量λ为鲁棒的，即鲁棒性函数RF(mij)=0。在此基础上，由式(14)可计算得系统的鲁棒型度量：
。
从仿真结果可以看出，由于m11没有增性摄动(摄动前后都是595)，所以，不用考虑其鲁棒性分析，也就是其鲁棒性度量RM(m11)=0；而对于除m11外的其余所有可摄动元，其鲁棒性度量RM(mij)＞0，对应于稳态参量λ对可摄动元mij都为鲁棒性的；鲁棒性度量RM(mij)越大，对应于稳态参量λ对可摄动元mij的鲁棒性程度越高。由此可见，系统在mij有较大摄动的情况下其鲁棒性都比较高。
经过对所选择的生产周期最小的铝板轧制队列进行鲁棒性能分析可知，对生产周期λ=595 min的排列P3P2P1，在系统轧制时间有较大改变的情况下仍然可以获得整个系统的不变的周期稳态输出，从而证明在6种排队方式中，该调度方案是最优的。
4 结 论
a. 极大代数法可充分结合排队论和矩阵分析的方法，实现对多队列条件下的离散事件动态系统的分析。与其他分析方法相比，更容易通过计算机编程 实现。
b. 运用周期配置理论，对铝板轧制系统的周期性稳态性能进行了摄动分析，通过分析不同队列周期性稳态参量的鲁棒性。可得出最优队列。这样分析使得极大代数方法更加贴近于工程实际，考虑了参数漂移的情形，能较好地处理工程问题。
c. 针对铝板轧制过程的复杂性，可考虑运用极大代数法将线性理论与非线性模型及人工智能算法相结合，减少运算的复杂度，使该方法具有更大的推广 价值。
参考文献：
[1] 付振南, 许庆彦, 熊守美. 基于概率捕获模型的元胞自动机方法模拟镁合金枝晶生长过程[J]. 中国有色金属学报, 2007, 17(10): 1567-1573.
FU Zhen-nan, XU Qing-yan, XIONG Shou-mei. Numerical simulation on dendrite growth process of Mg alloy using cellular automaton method based on probability capturing model[J]. The Chinese Journal of Nonferrous Metals, 2007, 17(10): 1567-1573.
[2] 王仲君, 王能超, 冯 飞, 等. 元胞自动机的演化行为研究[J]. 计算机应用研究, 2007, 24(8): 38-41.
WANG Zhong-jun, WANG Neng-chao, FENG Fei, et al. Research on evolved behavior of cellular automata[J]. Application Research of Computers, 2007, 24(8): 38-41.
[3] 郑 忠, 徐 乐, 高小强. 基于元胞自动机的车间天车调度仿真模型[J]. 系统工程理论与实践, 2008, 28(2): 137-142.
ZHENG Zhong, XU Le, GAO Xiao-qiang, Simulation model of crane scheduling in workshop based on cellular automata[J]. Systems Engineering: Theory & Practice, 2008, 28(2): 137-142
[4] 陈慧灵, 王宪增, 邹宽城. 基于Petri网的工作流过程建模[J]. 计算机工程与科学, 2008, 30(5): 92-94.
CHEN Hui-ling, WANG Xian-zeng, ZOU Kuan-cheng. Workflow process modeling based on petri nets[J]. Computer Engineering & Science, 2008, 30(5): 92-94.
[5] 马福民, 王 坚. 面向企业能源消耗过程的模糊Petri网模型研究[J]. 计算机集成制造系统, 2007, 13(9): 1679-1685.
MA Fu-min, WANG Jian. Fuzzy Petri nets model oriented to enterprise energy consumption process[J]. Computer Integrated Manufacturing Systems, 2007, 13(9): 1679-1685.
[6] CAO Xi-ren. From perturbation analysis to Markov decision processes and reinforcement learning[J]. Discrete Event Dynamic Systems: Theory and Applications, 2003, 13(1): 9-39.
[7] 崔 静. 随机环境中马氏链的状态研究[J]. 重庆工商大学学报: 自然科学版, 2008, 25(1): 23-24.
CUI Jing. Properties of states for Markov Chains in random environments[J]. Journal of Chongqing Technology Business University: Nature Science Edition, 2008, 25(1): 23-24.
[8] 王 飞, 冯祖仁, 胡奇英. 基于马氏决策过程的概率离散事件系统最优控制[J]. 控制理论与应用, 2007, 24(6): 895-901.
WANG Fei, FENG Zu-ren, HU Qi-ying. Optimal control of probabilistic discrete event systems on Markov decision process[J]. Control Theory and Applications, 2007, 24(6): 895-901.
[9] 程志君, 郭 波. 基于半Markov决策过程的劣化系统检测与维修优化模型[J]. 自动化学报, 2007, 33(10): 1101-1104.
CHENG Zhi-jun, GUO Bo. Optimization of inspection and maintenance policy for deteriorating system with semi-Markov decision process[J]. Acta Automatica Sinica, 2007, 33(10): 1101-1104.
[10] 李勇建, 涂奉生, 贾春福. 循环排队网络的极大代数描述、稳定性与扰动分析[J]. 控制理论与应用, 2002, 19(4): 527-531.
LI Yong-jian, TU Feng-sheng, JIA Chun-fu. Max-algebra description, stability and perturbation analysis of cyclic queue network[J]. Control Theory and Applications, 2002, 19(4): 527-531.
[11] 王 飞, 冯祖仁, 胡奇英. 离散事件系统的混合可靠分散监控[J]. 控制理论与应用, 2008, 25(1): 14-20.
WANG Fei, FENG Zu-ren, HU Qi-ying. Mixed reliable decentralized supervisory control of discrete event systems[J]. Control Theory and Applications, 2008, 25(1): 14-20.
[12] 李慧中, 梁霄鹏, 张新明, 等. 2519 铝合金热变形组织演化[J]. 中国有色金属学报, 2008, 18(2): 226-230.
LI Hui-zhong, LIANG Xiao-peng, ZHANG Xin-ming, et al. Microstructure evolution of 2519 aluminum alloy during hot deformation[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(2): 226-230.
[13] ZHANG Xin-ming, YE Ling-ying, LIU Ying-wei, et al. Formation mechanism of gradient-distributed particles and their effects on grain structure in 01420 Al-Li alloy[J]. Journal of Central South University of Technology, 2008, 15(2): 147-152.
[14] LI Zhi-hui, XIONG Bai-qing, ZHANG Yong-an, et al. Microstructural evolution of aluminum alloy 7B04 thick plate by various thermal treatments[J]. Transactions of Nonferrous Metals Society of China, 2008, 18(1): 40-45.
[15] 蔡 雁, 吴 敏, 杨 静, 等. 基于优化调度模型的焦炉推焦计划编制方法[J]. 中南大学学报: 自然科学版, 2007, 38(4): 745-750.
CAI Yan, WU Min, YANG Jing, et al. Coke oven working planning based on optimization scheduling models[J]. Journal of Central South University: Science and Technology, 2007, 38(4): 745-750.
[16] 戴华平. 多尺度条件下制造系统的监控器设计—极大代数方法[J]. 系统工程理论与实践, 2005, 25(6): 49-53.
DAI Hua-ping. Designing a supervisory controller for multi-scale manufacturing systems: A max-plus algebraic method[J]. Systems Engineering: Theory & Practice, 2005, 25(6): 49-53.
[17] 孙志敏, 陈文德, 于洪年. 极大代数上线性系统的最小实现[J]. 控制与决策, 2006, 21(5): 521-526.
SUN Zhi-min, CHEN Wen-de, YU Hong-nian. Minimal realization in linear system of max-algebra[J]. Control and Decision, 2006, 21(5): 521-526.
[18] WANG Ya-lin, MA Jie, GUI Wei-hua, et al. Multi-objective intelligent coordinating optimization blending system based on qualitative and quantitative synthetic model[J]. Journal of Central South University of Technology, 2006, 13(5): 552-557.
[19] 陈文德, 张迪生. 极大代数方法在轧钢厂中的应用[J]. 自动化学报, 1995, 21(1): 99-103.
CHEN Wen-de, ZHANG Di-sheng. An Application on max-algebra method in DEDS of the steel rolling mill[J]. Acta Automatica Sinica, 1995, 21(1): 99-103.
[20] 李 一, 李东海, 曾河华. 机炉协调控制系统的鲁棒性能分析[J]. 清华大学学报: 自然科学版, 2007, 47(5): 674-677.
LI Yi, LI Dong-hai, ZENG He-hua. Robustness analysis of a boiler-turbine control system[J]. Journal of Tsinghua University: Science and Technology, 2007, 47(5): 674-677.
[21] 吴秀丽, 孙树栋, 余建军, 等. 多目标柔性作业车间调度优化研究[J]. 计算机集成制造系统, 2006, 12(5): 731-736.
WU Xiu-li, SUN Shu-dong, YU Jian-jun, et al. Research on multi-objective optimization for flexible job shop scheduling[J]. Computer Integrated Manufacturing Systems, 2006, 12(5): 731-736.
[22] 韩江洪, 张亚琼, 魏振春, 等. 基于规则的离散事件系统模型与规则匹配研究[J]. 系统仿真学报, 2008, 20(6): 1394-1396.
HAN Jiang-hong, ZHANG Ya-qiong, WEI Zhen-chun, et al. Research of rule-based model of discrete event system and rule matching[J]. Journal of System Simulation, 2008, 20(6): 1394-1396.
[23] 李秀英, 邢 伟, 张庆灵. 严格正实广义系统的鲁棒性分析与输出反馈控制[J]. 东北师范大学学报: 自然科学版, 2007, 39(4): 33-37.
LI Xiu-ying, XING Wei, ZHANG Qing-ling. Robustness analysis and output feedback control for strictly positive real descriptor systems[J]. Journal of Northeast Normal University: Natural Science Edition, 2007, 39(4): 33-37.
收稿日期：2008-06-29；修回日期：2008-10-05
基金项目：国家“973”计划项目(2002CB312200)；国家自然科学基金资助项目(60874008)
通信作者：胡 扬(1978-)，男，湖南长沙人，博士研究生，讲师，从事离散事件动态系统和人工智能的研究；电话：0731-8879702；E-mail: foxgoat@yahoo.com.cn
