硬质合金烧结-热等静压炉的优化
陈 祎1,罗永浩1,时章明2,段 佳1,季俊杰1
(1. 上海交通大学 机械与动力工程学院,上海,200240;
2. 中南大学 能源与动力工程学院,湖南 长沙,410083)
摘 要:建立了硬质合金烧结-热等静压炉内传热的三维非稳态数值仿真模型,对炉内的温度场进行仿真与优化。提出分段仿真方法,即在真空加热阶段采用层流模型和S2S辐射模型,在低压和高压氩气加热阶段采用k-ε湍流模型和DTRM辐射模型。结果表明:仿真结果与实验结果相吻合;石墨筒内温度分布不均匀,其主要原因是石墨舟和烧结制品布置方式以及石墨筒结构的不合理。实验中提出优化措施,使烧结制品表面温度偏差在真空阶段减小约10 K,在气体加热阶段减小到±7 K以内,从而可提高烧结质量。
关键词:硬质合金;烧结-热等静压炉;温度场;数值仿真;优化
中图分类号:TK175 文献标识码:A 文章编号:1672-7207(2007)02-0320-06
Optimization of cemented carbide sinter-HIP furnace
CHEN Yi1, LUO Yong-hao1, SHI Zhang-ming2, DUAN Jia1, JI Jun-jie1
(1. School of Mechanical Engineering, Shanghai Jiaotong University, Shanghai 200240, China;
2. School of Energy and Power Engineering, Central South University, Changsha 410083, China)
Abstract: A three dimensional unsteady numerical model of cemented carbide sinter-HIP furnace was established. The temperature field was simulated and optimized with this model. Dividual simulation method was put forward in the model. In this method laminar flow model and S2S radiation model were used in vacuum heating stage, and k-ε turbulence model and DTRM model were adopted in low-pressure and high-pressure argon heating stages. The simulation results are in consistence with the experiment results, and shows that the temperature distribution in the graphite box is non-uniform, which is mainly caused by the illogical location of the graphite boards and the sintered products and the unreasonable structure of the graphite box. Therefore, the measures to optimize the temperature were brought forward, and the temperature difference reduction of the sintered product surface is reduced to 10 K during the vacuum heating stage, and the temperature difference of sintered product surface falls to ±7 K during the gas heating stage, which can enhance the sintering quality.
Key words: cemented carbide; sinter-HIP furnace; temperature field; numerical simulation; optimization
低压热等静压烧结(Sinter-HIP)工艺或过压烧结(Over pressure sintering)工艺,是在低于常规热等静压的压力(大约6 MPa)下对工件同时进行热等静压和烧结的工艺[1-2]。烧结-热等静压炉具有真空炉和热等静压炉的特点,它是生产轧辊、顶锤、压缸等高性能硬质合金产品的重要设备。目前,高性能硬质合金产品的质量缺陷主要为欠烧、过烧和含碳量不均匀等,其主要原因是烧结炉内温度不均匀及炉内气体流动不合理[3-4]。一些研究者认为,炉内的温度均匀性是影响高性能硬质合金产品质量的重要因素[5-6]。
结合烧结-热等静压炉的运行过程和工艺制度,炉内的热工过程可分为4个阶段:
a. 真空加热阶段。炉内压力基本保持恒定,压力很低(约2 Pa),气体量很小,炉内传热以导热和辐射为主;
b. 低压Ar气体加热阶段。炉内空间的压力达到4 kPa,炉内传热以辐射和自然对流为主;
c. 高压Ar气体加热阶段。炉内的压力达到5.5 kPa,烧结制品处于液相烧结阶段,炉内传热以辐射和自然对流为主,炉内温度较高,自然对流换热加剧;
d. 高压Ar冷却阶段。利用高压氩气对炉内进行冷却。
本文作者针对株洲硬质合金集团有限公司从德国PVA公司引进的COD733R型烧结-热等静压炉,研究石墨筒内温度场的分布均匀性,并提出相应的优化措施。
1 数值仿真模型
1.1 物理模型
在仿真过程中,对物理模型进行如下假设:忽略滚轮、石墨柱等对传热贡献不大的结构;忽略保温筒、石墨筒与炉内支撑结构之间的缝隙;因每层的石墨舟彼此紧靠,将其视为一整块石墨舟;忽略炉内各结构和烧结制品的体积变化[7-8]。以保温筒为边界建立模型,炉体结构见图1,石墨舟和烧结制品结构见图2。
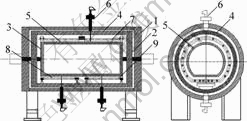
1—炉门; 2—保温筒门; 3—石墨筒门; 4—保温筒;
5—石墨筒; 6—控制带热电偶; 7—顶部发热体组;
8—底部发热体组1; 9—底部发热体组2
图1 炉体结构示意图
Fig.1 Schematic diagram of furnace
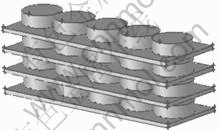
图2 石墨舟与烧结制品的结构
Fig.2 Structure of graphite boards and sintered products
1.2 数学模型
烧结-热等静压炉的热工过程非常复杂,不同的热工过程主要传热方式不同,因此,采用分段仿真计算,计算各阶段的瑞利数Ra并判断其气体流动状态:当Ra小于108时,为层流流动;当Ra增大到108到1010之间时,气体流动就过渡到湍流,计算结果见表1。再根据各阶段的传热特点,采用相应的模型:真空加热阶段采用层流模型和表面辐射模型;低压和高压氩气加热阶段采用k-ε湍流模型(该模型较具有适应性广、计算量相对较小、精度合理,能满足工程应用的要求)和离散传播辐射模型[9-16]。
表1 各阶段瑞利数的数量级估算结果
Table 1 Results of Rayleigh in every stage

控制方程组包括连续性方程、动量方程、能量方程、k-ε湍流模型方程。此外,在气体的自然对流过程中,炉内不存在燃烧,气体可认为是理想气体,遵守理想气体状态方程。
连续性方程:

1.3 边界条件和初始条件
以保温筒外壁为边界,采用第一类边界条件,即保温筒的外壁温度与时间的函数关系;初始条件为炉子功率加热器开始送电时保温筒外壁的温度。
2 仿真结果与实验验证
图3和4所示为仿真计算的温度分布图。可以看出,烧结制品表面温度分布呈现出外高内低、上高下低的趋势。上下两层烧结制品表面温度略高,尤其是顶层烧结制品温度较高,易出现过烧现象;而中间两层和靠近炉门侧的烧结制品温度较低,易出现欠烧现象,影响烧结制品的质量。

图3 烧结制品表面温度分布图(180 min)
Fig.3 Simulated temperature distribution of sintered products surface (180 min)
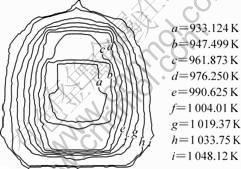
图4 石墨筒内部空间x=0截面的温度分布(180 min)
Fig.4 Simulated temperature distribution of surface x=0 in graphite box (180 min)
表2所示为仿真计算的烧结温度表面温度偏差,可以看出,进入低压氩气阶段之后,烧结制品表面温差减小,高压氩气阶段烧结制品表面平均温差最低。这是因为气体湍流换热促进了炉内温度场的均匀性。因此,在工艺允许的前提下,可适当增加气体量,加强炉内气体对流换热。
表2 仿真计算的烧结制品表面温度偏差
Table 2 Temperature difference of sintered products surface calculated by model

为了验证仿真结果的正确性,在石墨筒内部空间布置7个测点,即炉子本体的3支WRe5-WRe26控制热电偶和另外放置的4支NiCr-NiSi铠装热电偶,见图5和6;图5中长方体为石墨筒内的有效加热空间,其长×宽×高为555 mm×550 mm×1500 mm;图6中的3个测点位于石墨筒外。
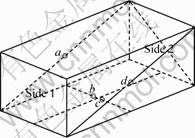
a,d—侧面中心点,b,c—靠近底面中心的2个点,
与中心位置的距离为5 cm
图5 实验热电偶测点位置(4点)
Fig.5 Location of thermocouples
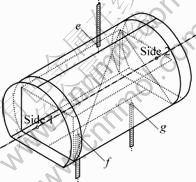
e—顶部控制热电偶,距石墨筒外壁15 mm;f—底部靠近炉门1端控制热电偶,距石墨筒外壁5 mm;g—底部靠近炉门2端控制热电偶,与石墨筒外壁相距5 mm
图6 控制热电偶测点位置(3点)
Fig.6 Location of thermocouples
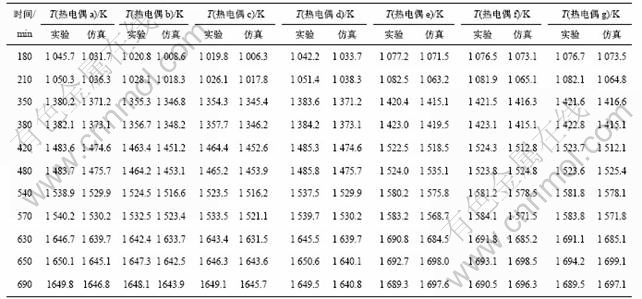
表3所示为7支热电偶温度的实测值与仿真值。可以看出,实测值与仿真值较好吻合,最大偏差不超过15 K。
表3 热电偶测点处温度的实验值与仿真值
Table 3 Temperature at location of thermocouples obtained by test and simulation
3 炉内温度场的仿真优化
3.1 石墨舟和烧结制品的优化
石墨舟和烧结制品的位置对石墨筒内温度场有较大的影响。为了提高烧结制品表面温度均匀性,对石墨舟和烧结制品的布置位置和结构进行优化。优化前后的情况见于表4。其中:工况1为实际生产工况,工况2和3为优化工况。
从表4可以看出,在同样热工条件下,适当改变石墨舟的尺寸有利于提高烧结制品表面的温度均匀性,但增大石墨舟间的间距不一定能提高烧结制品表面温度的均匀性;在炉子装载量为5×4的情况下,工况3的温度场均匀性最佳,优化后的表面温差在气体加热阶段减少到±7 K以内。
表4 仿真参数与结果
Table 4 Parameters and results of simulation

3.2 石墨筒的结构优化
采用如图7(a)所示的结构,烧结制品两侧形成了很大的剩余空间,不利于中间两层烧结制品接收石墨筒壁的辐射,因此,可改变石墨筒结构,减小中部烧结制品与石墨筒壁的距离,将石墨筒改成图7(b)所示的结构。
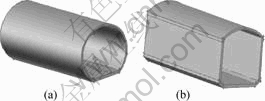
(a) 改进前;(b) 改进后
图7 改进前后的石墨筒结构图
Fig.7 Graphite box structure before and after optimization
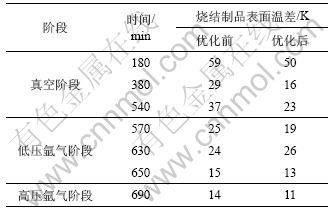
由表5可以看出,改进石墨筒结构后,温度偏差在真空阶段平均减小10 K左右,提高了烧结制品表面温度均匀性。
表5 石墨筒结构改进前后烧结制品表面温差
Table 5 Temperature difference of sintered products surface before and after optimization
4 结 论
a. 对硬质合金烧结热等-静压炉内温度场的仿真计算表明:烧结制品表面温度的分布表现为外高内低,上高下低。这与实验结果相吻合。
b. 筒内的温度分布不均匀。上下两层尤其是顶层烧结制品温度偏高,易出现过烧现象;靠近炉门侧的烧结制品温度偏低,易出现欠烧现象,影响产品的烧结质量。其原因是炉内石墨舟和烧结制品布置方式及石墨筒结构的不合理。在工艺允许的条件下,可适当增加气体加热阶段炉内的气体量,提高石墨筒内温度均匀性。
c.在单炉装载量为5×4的情况下,确定石墨舟的最佳结构尺寸(长×宽×高)为:300 m×300 m×30 mm;优化后烧结制品表面温度均匀性得到提高,表面温度偏差在气体加热阶段减少到±7 K以内,提高了烧结产品质量;通过改进石墨筒结构,温度偏差在真空阶段平均减小10 K左右,进一步提高了烧结制品表面温度均匀性。
参考文献:
[1] 王国栋. 硬质合金烧结原理[M]. 北京: 冶金工业出版社, 1988.
WANG Guo-dong. Cemented carbide sintering theory[M]. Beijing: Metallurgical Industry Press, 1988.
[2] Wofshtein M. Low pressure sinter-HIP system feature computer control[J]. MPR, 1987, 12(2): 880-886.
[3] 刘永福. 硬质合金的烧结气氛及其控制[J]. 硬质合金, 1996, 13(3): 176-179.
LIU Yong-fu. Sintering atmosphere of cemented carbide and its control[J]. Cemented Carbide, 1996, 13(3): 176-179.
[4] 洪殷程, 李学芳. 硬质合金氢气烧结的变形机理及其控制[J]. 硬质合金, 2000, 17(3): 156-160.
HONG Yin-cheng, Li Xue-fang. The cause and control of deformation of cemented carbide in hydrogen sintering[J]. Cemented Carbide, 2000, 17(3): 156-160.
[5] Wofshtein M. World first for pfeiffer pressure sintering furnace[J]. MPR, 1986, 11(9): 687-693.
[6] Wofshtein M. Sinter-HIP system for processing cemented carbides[J]. MPR, 1987, 12(5): 373-377.
[7] 陈 祎. 硬质合金烧结-热等静压炉内温度场的实验研究与数值仿真[D]. 长沙: 中南大学能源与动力工程学院, 2005.
CHEN Yi. Experimental Study and Numerical Simulation of Temperature Field in a Sinter-HIP Furnace [D]. Changsha: School of Energy and Power Engineering, Central South University, 2005.
[8] 刘余庆. 硬质合金烧结-热等静压炉内温度场仿真及结构优化[D] . 长沙: 中南大学能源与动力工程学院, 2006.
LIU Yu-qing. Numerical Simulation of Temperature Field and Optimization of Structure in a Sinter-HIP Furnace[D]. Changsha: School of Energy and Power Engineering, Central South University, 2006.
[9] Coelho P J, Goncalves J M, Carvalho M G. Modeling of radiative heat transfer in enclosures with obstacles[J]. International Journal of Heat Mass Transfer, 1998, 41(4): 745-756.
[10] 李光正, 李 贵. 封闭腔内自然对流数值方法研究[J]. 华中科技大学学报: 城市科学版, 2002, 19(4): 20-22.
LI Guang-zheng, LI Gui. Study of the numerical method for solving the natural convection in an enclosure[J]. J of Huazhong Univ of Sci & Tech: Urban Science Edition, 2002, 19(4): 20-22.
[11] 张 宁, 李光正. 一种改进的SIMPLER算法[J]. 华中科技大学学报: 城市科学版, 2002, 19(2): 28-31.
ZHANG Ning, LI Guang-zheng. A modified SIMPLER calculation method[J]. J of Huazhong Univ of Sci & Tech: Urban Science Edition, 2002, 19(2): 28-31.
[12] 顾明言, 章明川, 范卫东, 等. 辐射离散传播法在三维圆柱腔体辐射传热计算中的应用[J]. 热能动力工程, 2005, 20(5): 482-486.
GU Ming-yan, ZHANG Ming-chuan, FAN Wei -dong, et al. The application of a radiation discrete transfer method for the radiation heat transfer calculation of a three-dimensional cylindrical cavity body[J]. Journal of Engineering for Thermal Energy and Power, 2005, 20(5): 482-486.
[13] 李宏顺, 周怀春, 陆继东, 等. 炉膛辐射换热计算的一种改进的离散传递法[J]. 中国电机工程学报, 2003, 23(4): 162-166.
LI Hong-shun, ZHOU Huai-chun, LU Ji-dong, et al. An improved discrete transfer method for radiative heat transfer in furnaces[J]. Proceedings of CSEE, 2003, 23(4): 162-166.
[14] 任泽霈, 张立宁, 贾 力. 封闭空间中自然对流与导热、辐射的复合换热[J]. 工程热物理学报, 1988, 9(3): 245-250.
REN Ze-pei, ZHANG Li-ning, JIA Li. Natural convection in enclosure combined with conduction and radiation[J]. Journal of Engineering Thermophysics, 1988, 9(3): 245-250.
[15] 陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 1988.
TAO Wen-quan. Numerical heat transfer [M]. Xi’an: Xi’an Jiaotong University Press, 1988.
[16] 梅 炽. 有色冶金炉窑仿真与优化[M]. 北京: 冶金工业出版社, 2001.
MEI Chi. Simulation and optimization of nonferrous metallurgical furnace[M]. Beijing: Metallurgical Industry Press, 2001.
收稿日期:2006- 08-06
作者简介:陈 祎(1980-),男,湖南株洲人,博士研究生,从事能源利用的研究
通讯作者:陈 祎,男,博士研究生;电话:021-34205702;E-mail:csuchris@126.com