SOC estimation based on data driven exteaded Kalman filter algorithm for power battery of electric vehicle and plug-in electric vehicle
来源期刊:中南大学学报(英文版)2019年第6期
论文作者:苏卫星 刘芳 马杰 CHEN Han-ning(陈瀚宁) 田慧欣 李春青
文章页码:1402 - 1415
Key words:state of charge; extended Kalman filter; autoregressive model; power battery
Abstract: State of charge (SOC) estimation has always been a hot topic in the field of both power battery and new energy vehicle (electric vehicle (EV), plug-in electric vehicle (PHEV) and so on). In this work, aiming at the contradiction problem between the exact requirements of EKF (extended Kalman filter) algorithm for the battery model and the dynamic requirements of battery mode in life cycle or a charge and discharge period, a completely data-driven SOC estimation algorithm based on EKF algorithm is proposed. The innovation of this algorithm lies in that the EKF algorithm is used to get the SOC accurate estimate of the power battery online with using the observable voltage and current data information of the power battery and without knowing the internal parameter variation of the power battery. Through the combination of data-based and model-based SOC estimation method, the new method can avoid high accumulated error of traditional data-driven SOC algorithms and high dependence on battery model of most of the existing model-based SOC estimation methods, and is more suitable for the life cycle SOC estimation of the power battery operating in a complex and ever-changing environment (such as in an EV or PHEV). A series of simulation experiments illustrate better robustness and practicability of the proposed algorithm.
Cite this article as: LIU Fang, Ma Jie, SU Wei-xing, CHEN Han-ning, TIAN Hui-xin, LI Chun-qing. SOC estimation based on data driven exteaded Kalman filter algorithm for power battery of electric vehicle and plug-in electric vehicle [J]. Journal of Central South University, 2019, 26(6): 1402-1415. DOI: https://doi.org/10.1007/s11771-019-4096-5.

ARTICLE
J. Cent. South Univ. (2019) 26: 1402-1415
DOI: https://doi.org/10.1007/s11771-019-4096-5

LIU Fang(刘芳)1, 2, 3, Ma Jie(马杰)1, SU Wei-xing(苏卫星)1, CHEN Han-ning(陈瀚宁)1,TIAN Hui-xin(田慧欣)1, LI Chun-qing(李春青)1
1. School of Computer Science & Technology, Tianjin Polytechnic University, Tianjin 300387, China;
2. Tianjin Qingyuan Electric Vehicle Limited Liability Company, Tianjin 300457, China;
3. Control Theory and Control Engineering, Tianjin University, Tianjin 300350, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: State of charge (SOC) estimation has always been a hot topic in the field of both power battery and new energy vehicle (electric vehicle (EV), plug-in electric vehicle (PHEV) and so on). In this work, aiming at the contradiction problem between the exact requirements of EKF (extended Kalman filter) algorithm for the battery model and the dynamic requirements of battery mode in life cycle or a charge and discharge period, a completely data-driven SOC estimation algorithm based on EKF algorithm is proposed. The innovation of this algorithm lies in that the EKF algorithm is used to get the SOC accurate estimate of the power battery online with using the observable voltage and current data information of the power battery and without knowing the internal parameter variation of the power battery. Through the combination of data-based and model-based SOC estimation method, the new method can avoid high accumulated error of traditional data-driven SOC algorithms and high dependence on battery model of most of the existing model-based SOC estimation methods, and is more suitable for the life cycle SOC estimation of the power battery operating in a complex and ever-changing environment (such as in an EV or PHEV). A series of simulation experiments illustrate better robustness and practicability of the proposed algorithm.
Key words: state of charge; extended Kalman filter; autoregressive model; power battery
Cite this article as: LIU Fang, Ma Jie, SU Wei-xing, CHEN Han-ning, TIAN Hui-xin, LI Chun-qing. SOC estimation based on data driven exteaded Kalman filter algorithm for power battery of electric vehicle and plug-in electric vehicle [J]. Journal of Central South University, 2019, 26(6): 1402-1415. DOI: https://doi.org/10.1007/s11771-019-4096-5.
1 Introduction
Battery management system (BMS), which is crucial for power batteries of new energy vehicles, is used to monitor the key states of power battery (such as state of charge (SOC), state of health (SOH), and SOF (state of function)) and optimize its usage in order to ensure the safety of the battery while operating at the best condition. Among that, SOC estimation is one of the most basic functions of a BMS. Up to now, many studies have been carried out on it and the existing research results can be divided into two main categories: the Foundation item: Projects(51607122, 51378350) supported by the National Natural Science Foundation of China; Project(BGRIMM-KZSKL-2018-02) supported by the State Key Laboratory of Process Automation in Mining & Metallurgy/Beijing Key Laboratory of Process Automation in Mining & Metallurgy Research, China; Project(18JCTPJC63000) supported by Tianjin Enterprise Science and Technology Commissioner Project, China; Project(2017KJ094, 2017KJ093) supported by Tianjin Education Commission Scientific Research Plan Project, China; Project(17ZLZXZF00280) supported by Tianjin Science and Technology Project, China; Project(18JCQNJC77200) supported by Tianjin Province Science and Technology projects, China; Project(2017YFB1103003, 2016YFB1100501) supported by National Key Research and Development Plan, China model-based methods like Kalman filtering (KF) [1, 2] and the data-based methods like the current integration method [3, 4]. As for the model-based method, since the traditional KF algorithm requires the state model must be linear [2, 5], it is not suitable for the vast majority of nonlinear problem solving [6], and thus the extended Kalman filter algorithm (EKF) [6, 7] comes into being which solves the nonlinear problems by approximating the nonlinear model to a linear model in the form of Taylor series [8]. However, both the KF and the EKF algorithm need the accurate internal parameters of the power battery, and the main way to obtain them is battery charging and discharging experiment, which also has two main limitations: one is that battery parameters obtained by the laboratory cannot accurately reflect the status of all the batteries due to the poor consistency of the battery in the production process; the other is the internal parameters of battery would inevitably change with battery aging. In a word, a simple EKF algorithm is not suitable for solving the SOC estimation problem of electric vehicle. As for the data-driven method, represented by the current integral method, the main problem is that accumulative errors are inevitable [3], although so many efforts have been made, such as adding various kinds of online SOC correction methods [5, 9], or preprocessing the collected data first.
Moreover, considering the application effect and performance of practical engineering and operating modes, the design requirements and objectives of SOC estimation method also need to meet the following conditions:
1) Due to the complex and changeable conditions during the charge and discharge process of electric vehicle, which makes the signal from EV has a large transient value and much noise, the SOC estimation algorithm for electric vehicle is required to have good robustness and capability to quickly converge [10].
2) Since the same SOC estimation method will be applied to BMS for mass production of electric vehicle, and to power battery for its life cycle, the estimation method should have strong versatility and the ability of learning and updating online.
3) Due to the drastic electric current change of electric vehicles and the high peak transient current, the method is required to complete the estimation process in a short time. That is to say the algorithm complexity is as low as possible.
Based on the above analysis, this paper proposes a data-driven EKF-based method for power battery SOC estimation of the BMS for electric vehicles. The characteristics and advantages are summarized as follows:
1) The method is a combination of data-driven method and model-driven method. This combination is not a simple patchwork, but the advantages of each method while avoiding their shortcomings.
2) The method can identify the variation of the internal characteristics of the power battery online without the need of large amount of battery performance experimental data. Meanwhile, this mechanism also brings about strong dynamic characteristics and makes the method suitable for solving the SOC estimation problem of the power battery with lower computational complexity (since the parameter of battery that reflects the health of battery can be updated dynamically).
3) Without the need of setting the initial SOC value of the power battery, the method has a closed-loop self-correction capability for the estimation of the SOC and therefore converges to an accurate SOC value in a short period of time. This mechanic also makes the algorithm have good robustness and suitable for SOC estimation of power battery using in electric vehicles with complex operating conditions and drastic current changes.
The remainder of the manuscript will describe the complete algorithm in detail. First, from the exact equivalent circuit of the power battery, which includes part of the black box model, the equation of state and the observation equation of the EKF algorithm are given. Second, we introduce the data-driven dynamic identification and modeling algorithm for building a black box model, and use the simulation to verify the effectiveness of the algorithm. Third, the effective combination of data-driven algorithm and model-based EKF algorithm is realized. Finally, simulation experiments based on real data and model data are performed to verify the effectiveness, practicability and accuracy of the algorithm.
2 Extended Kalman filter model for power battery
Just as mentioned above, EKF-based SOC estimation is highly depended on the establishment of a reasonable battery model [11]. In other words, the accuracy of the model is the prerequisite for guaranteeing the accuracy of SOC estimation [6]. Therefore, considering the characteristics of poor consistency of the battery and the special needs that SOC estimation for the battery of EV or PHEV should be done during the whole life cycle, we propose a power battery equivalent circuit with a black box structure, and build a battery model based on this equivalent circuit. The equivalent circuit with black box is shown in Figure 1.
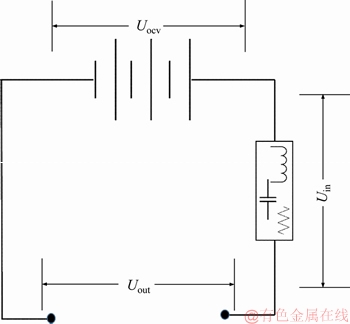
Figure 1 Electric vehicle battery equivalent circuit
In Figure 1, Uocv represents the electromotive force of the battery, generally called as the open circuit voltage. And we use Uin to denote the internal voltage drop caused by battery internal impedance. In this work, we think the battery internal impedance as a parameter which cannot obtain accurate value since it will keep changing with temperature, current, SOH, SOC and so many factors. And the Uout denotes the observed power battery external voltage value, which can be measured by sensor. The relationship of them can be writen as:
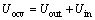 (1)
(1)
where Uocv and SOC have a correspondence relationship which changes with temperature. The relationship of Uocv, SOC (Cso) and temperature can be described by Eq. (2) and gotten by least square fitting algorithm (LSF) [12, 13].
 (2)
(2)
In Eq. (2), T denotes the temperature of the battery, f(·) denotes a nonlinear functional relationship.
It is obvious that the value of Uin is determined by the current and the impedance [14]. Comparing with the current, the battery internal impedance can be regarded as slow time-varying variables. That is to say, for a moment, we can regard the battery impedance as a constant. So at the beginning of time t (equals to t=1), corresponding to the power-up moment of EVs, the function relationship of Uin and current can be expressed as follow:
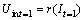 (3)
(3)
where r(·) denotes a black box model that reflect the dynamic battery internal impedance slow time-varying system. The input is the current of battery It and the output is the internal voltage Uint. When time goes on, Eq. (3) can be expressed in a recursive form as
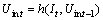 (4)
(4)
where h(·) is the recursive form of the black box model which reflects the dynamic battery internal impedance slow time-varying system. From Eq. (4), we can see that Uin at each moment can be expressed as a function, including the current value It of the current moment and Uin value of the previous moment. So we move Eq. (4) all the way forward by p steps to get:
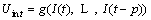 (5)
(5)
where g(·) is a black box model that represents the relationship between power battery internal voltage at time t and battery current values at last p time. We bring Eq. (2) and Eq. (5) into Eq. (1) to get the observation equation of EKF algorithm:
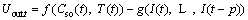 (6)
(6)
For the state equation of EKF algorithm, we use the equation of the current integration algorithm as
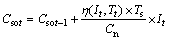 (7)
(7)
where η(It, Tt) represents the correction factor related to the charge-discharge rate and the temperature; Ts indicates the sampling period;Cn is nominal capacity of the power battery.
3 Data driven SOC estimation based on EKF algorithm
Equation (6) shows the observation equation of EKF algorithm with two nonlinear parts, the first part f(Csot, Tt) denotes open circuit voltage, and the second part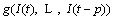 denotes power battery internal voltage.
denotes power battery internal voltage.
3.1 Dynamic updating method of EKF observation equation
3.1.1 Open circuit voltage function f(Csot, Tt)
Dynamic update method of open circuit voltage function f(Csot, Tt) is described in Figure 2.
According to Eq. (2), the nonlinear function f(·) represents the relationship between the open circuit voltage, SOC and temperature. Since SOH has little effect on the function f(·) during the power battery life cycle, we consider that the f(·) can be obtained offline once and continuously available throughout the full life cycle of the power battery. Traditional method is used to linearize it by performing a least square fit (LSF) on it first to get the exact expression of f(·) [15, 7], and then Taylor expansion at estimated SOC [6]. This procession is shown in Figure 2 in the condition of knowing the relationship of the open circuit voltage, SOC and temperature in Figure 3.
In Figure 2,the equation in the dashed box is one of the linearization formulas in the EKF algorithm and the CSOC value represents the linearized coefficient of the nonlinear observation equation [15]. It can be seen from the formula that it varies with the SOC value. Therefore, in the complete SOC estimation algorithm, CSOC is one of the parameters that need to be dynamically updated.
3.1.2 For battery internal voltage function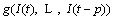
The nonlinear function 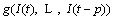 is considered as a slow time-varying system that reflects the internal impedance of the battery as a black box model. The currents of battery
is considered as a slow time-varying system that reflects the internal impedance of the battery as a black box model. The currents of battery 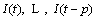 are regarded as the system input, and the output is the battery internal voltage Uint at time t. The function
are regarded as the system input, and the output is the battery internal voltage Uint at time t. The function 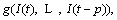 which reflects the state of internal impedance of battery, is slow time-varying, we use AR model to realize online dynamic fitting to obtain the internal battery voltage value Uint at time t and Eq. (5) can be rewritten as:
which reflects the state of internal impedance of battery, is slow time-varying, we use AR model to realize online dynamic fitting to obtain the internal battery voltage value Uint at time t and Eq. (5) can be rewritten as:
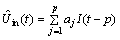 (8)
(8)
where p denotes the order of AR model, is the coefficient of AR model. From Eq. (8), we know that the coefficient of AR model
is the coefficient of AR model. From Eq. (8), we know that the coefficient of AR model  should be updated over time. In order to ensure that the AR model can accurately track the slow-time dynamic characteristics of battery internal impedance, an online iterative updating algorithm with forgetting factor is used to get the AR model coefficients at each moment. Online iterative updating algorithm is based on the idea of maximizing a posteriori[16, 17]. The objective function is:
should be updated over time. In order to ensure that the AR model can accurately track the slow-time dynamic characteristics of battery internal impedance, an online iterative updating algorithm with forgetting factor is used to get the AR model coefficients at each moment. Online iterative updating algorithm is based on the idea of maximizing a posteriori[16, 17]. The objective function is:

Figure 2 Function dynamic update architecture
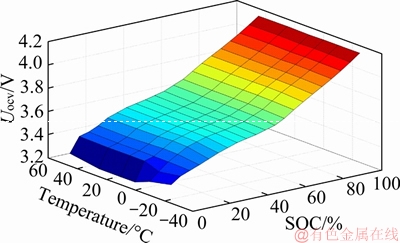
Figure 3 Open circuit voltage diagram under different temperatures and different SOC
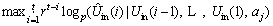 (9)
(9)
where r is the forgetting factor. From Eq. (9), we may find a trouble that the real values of internal voltage  cannot be gotten. For this problem, we use the estimation values
cannot be gotten. For this problem, we use the estimation values  by EKF to replace it. So Eqs. (8) and (9) are rewritten as:
by EKF to replace it. So Eqs. (8) and (9) are rewritten as:
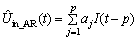 (10)
(10)
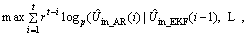
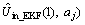 (11)
(11)
where  is the estimation values of battery internal voltage by AR model method, and
is the estimation values of battery internal voltage by AR model method, and  is the estimation value of battery internal voltage by EKF algorithm. The relationship between
is the estimation value of battery internal voltage by EKF algorithm. The relationship between  and
and  is:
is:
 (12)
(12)
where 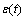 represents the fitting residual at time t.
represents the fitting residual at time t.
3.2 SOC online prediction algorithm based on AR-EKF algorithm
Before describing the complete AR-EKF algorithm, the following assumptions are given first and the rationality of the assumptions is illustrated as follows:
Assumptions:
1) The algorithm assumes that at the initial moment (t=0), the power battery current I(0) is zero, then the open-circuit voltage of the power battery is equal to the external voltage value, that means:  . So the initial SOC value Cso(0) (The initial SOC refers to the SOC value determined by BMS when the EV first powers on and it means that the whole life cycles only once for a power batter) can be determined by the f(·) function.
. So the initial SOC value Cso(0) (The initial SOC refers to the SOC value determined by BMS when the EV first powers on and it means that the whole life cycles only once for a power batter) can be determined by the f(·) function.
2) The noise intensity (especially for colored noise) of the observed signal collected by BMS is within a reasonable range. If the noise intensity floods the signal so that the signal is severely distorted, it is beyond the scope of this paper.
Reasonable explanations:
1) First of all, before completing the first power-on, the power battery should have been at rest for so long a time that there is no floating voltage. Second, nearly all of the power-up processes of EV are in a definite order, that is, completing the low voltage power-on first and then starting BMS to work and collect voltage and current signals, while the power battery relay is not closed, so this paper considers that the initial time of current I(0)=0 is reasonable. Under these conditions, it is reasonable and accurate to estimate the initial SOC value by the open-circuit voltage method in the absence of floating voltage and open circuit.
2) We all know that the traditional EKF algorithm is based on the assumption of Gaussian white noise. However, the research on the error analysis of EKF algorithm in non-Gaussian environment indicates [18] that the error performance of EKF algorithm in non-Gaussian environment and Gaussian environment is basically the same when the mean and variance are the same and the non-Gaussian is weak. In addition, in terms of algorithm, we also consider the processing strategy in non-Gaussian environment to some extent, so that the algorithm can alleviate the disadvantage of EKF algorithm in non-Gaussian environment to a certain extent.
Based on the above assumptions and the foregoing analysis, a complete SOC estimation process based on the AR-EKF algorithm is given in Figure 4, some details are explained as follows:
1) In the third step of initialization section “Calculating Uin(1) to Uin(n) by f(·) and Eq. (1)”, f(·) denotes the exact expression of f(·) by least square fitting algorithm.
2) For AR model initialization and update problem in the fourth step of initialization and the fourth step of estimation respectively, in this work, we use Eq. (11) as the objective function and adopt the method of maximum likelihood estimation to dynamically update AR model coefficient matrix A=[a1, …, ap], where p is the order of AR model, on-line to meet the slow time-varying characteristics of battery internal impedance. The initialization and update process is as follows [19, 20]:
Initialization process:
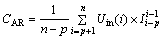 (13)
(13)
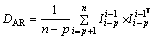 (14)
(14)
 (15)
(15)
where CAR is a p-dimensional vector; p is the order of AR model;  is a column vector of p currents
is a column vector of p currents 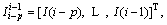 DAR is a p×p-dimensional matrix; and ARini is the initialization of the AR model coefficient matrix.
DAR is a p×p-dimensional matrix; and ARini is the initialization of the AR model coefficient matrix.

Figure 4 AR-EKF algorithm flow chart
AR model updating process:
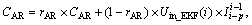
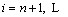 (16)
(16)
 (17)
(17)
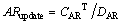 (18)
(18)
where rAR is forgetting factor.
3) For the second step of estimation section
“Calculating the estimation of Cso(i), by EKF algorithm using Eqs. (19)-(23)”, we give the main steps as follows [15]:
 (19)
(19)
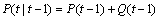 (20)
(20)

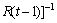 (21)
(21)
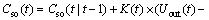
 (22)
(22)
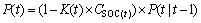 (23)
(23)
Equations (19)-(23) are the basic formulas of EKF algorithm, in which 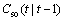 is a one-step estimate of
is a one-step estimate of  P(t) is the variance of the systematic error at time t,
P(t) is the variance of the systematic error at time t, 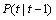 is a one-step estimate of P(t), K(t) is the gain for EKF algorithm, and Cso(t) can be got by the equation mentioned in Figure 2; Q in Eq. (20) and R in Eq. (21) are the variance of the observed error and the variance of the state error, respectively. We update Q and R with the “new information theory” as follows [21]:
is a one-step estimate of P(t), K(t) is the gain for EKF algorithm, and Cso(t) can be got by the equation mentioned in Figure 2; Q in Eq. (20) and R in Eq. (21) are the variance of the observed error and the variance of the state error, respectively. We update Q and R with the “new information theory” as follows [21]:
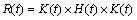 (24)
(24)
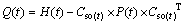 (25)
(25)
where H(t) is the “new information”, which is calculated by (t).
(t).
4) For the third step of estimation section “Calculating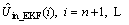 by f(·) and Eq. (1)”, the principle of solving idea is the same with “ Calculating Uin(1) to Uin(n) by f(·) and Eq. (1)” in the third step of initialization section.
by f(·) and Eq. (1)”, the principle of solving idea is the same with “ Calculating Uin(1) to Uin(n) by f(·) and Eq. (1)” in the third step of initialization section.
5) In this work, data noise is dealt based on the following strategies: firstly, the simple wavelet denoising algorithm is used to preprocess the data series I(t) and Uout(t) to achieve the purpose of effectively suppressing the intensity of colored noise and white noise rather than donoising completely; secondly, according to the conclusions of Ref. [18], when the noise is relatively weak, the EKF algorithm has little difference in the estimation error of the state values under the colored noise signal and the white noise signal, and is applicable to engineering applications.
4 Verification analysis
In this section, we've divided the verification process of the algorithm into two verifications based on battery model and real battery experiment.
4.1 Simulation analysis
4.1.1 Data generation process
In this part, we first introduce the methods and ideas of simulation and verification as follows:
First of all, a set of battery charging and discharging current data under NEDC conditions is collected from a real BMS of a pure EV. The battery model which comes from German DSPACE company are filled with LG's 18650 battery parameters, including the internal impedance curve of the battery under different temperature and SOC conditions, OCV curves, charge and discharge capacity coefficient values, charge and discharge power values, and the relationship of cycle number and internal resistance and so on, to achieve the purpose of simulating a real power battery. At last, we use the collecting current data as the input of the power battery model to get the power battery output, as shown in Figure 5.

Figure 5 Schematic of data generation process
The main reasons for using the battery model to simulate a real power battery and to generate simulation data are as follows:
1) If we use the battery model to simulate, the performance analysis of the proposed SOC estimation algorithm in various noise environments can be realized.
2) Since the battery model used here for data generation and comparison are industry-recognized in the engineering field, it is credible and reliable to carry out the experimental verification based on such model. Power battery model can give the real internal parameters, such as internal voltage change information, which makes the detailed analysis of AR-EKF algorithm more beneficial.
3) Since the observed value Uout(t) comes from the power battery model, the consistency in the verification process is fully guaranteed.
We intercept part of the data image shown in Figure 6.
4.2 Simulation in ideal state
Based on the model-generating experimental data without any contaminations, an experiment of SOC estimation using the proposed AR-EKF algorithm are implemented and the results are shown in Figure 7. From the figure we can find that since the current I(t) and the voltage signal Uout(t) used for simulation are ideal values without noise, the SOC estimation curve is smoother and with higher accuracy.
However, it can still be seen that there are some points with large SOC estimation errors around 2200 steps. In order to analyze the reason, we give the comparison result between battery internal voltage values  by AR model and real value Uin comes from battery model in Figure 8.
by AR model and real value Uin comes from battery model in Figure 8.
Comparing Figure 7 with Figure 8, we can find that when a larger SOC estimation error occurs, the internal voltage deviation of the power battery fitted by AR model also becomes larger, and this phenomenon usually happens when SOC is about 30%. The reason can be found in Figure 3, when the SOC is around 30%, the relationship between SOC and open circuit voltage is relatively flat. That is to say, even small voltage error will cause a large deviation of SOC. It can also be seen from Figure 8 that a deviation of 0.02 V occurs in the internal voltage value fitted by the AR model, leading to a 2.5% deviation of the SOC estimation value.
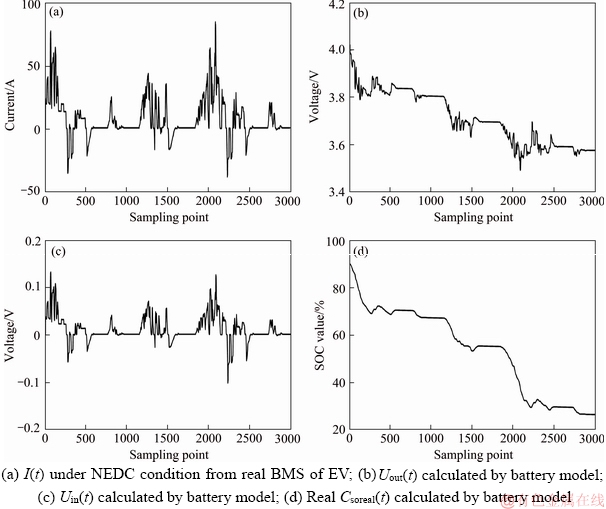
Figure 6 Experimental data for comparison and simulation:
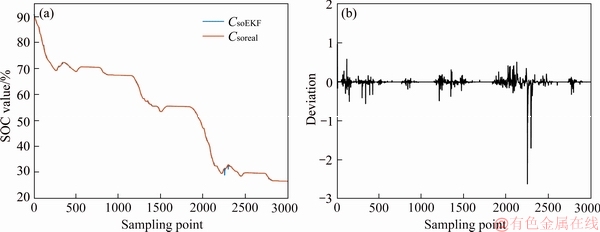
Figure 7 Comparing results between real SOC by battery model (a) and estimating SOC by AR-EKF algorithm (b)
Furthermore, we verify the convergence of the AR-EKF algorithm by changing the initial SOC value so that it deviates significantly from the true SOC value and then simulate it using the AR-EKF algorithm proposed in the paper. The results are shown in Figure 9.
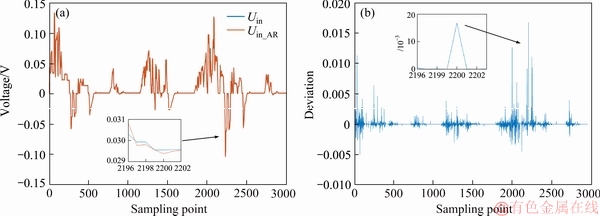
Figure 8 Comparing results between real internal voltage of battery model (a) and its estimating values by AR model (b)

Figure 9 Convergence verification results:
From the partially enlarged section of Figure 9, it can be seen clearly that the initial SOC values deviate significantly (deviation> 60%), but the AR-EKF algorithm converges rapidly in about 10 steps.
4.3 Simulation in noise environment
4.3.1 Colored noise
As we know that noise in real system must be non-white noise. So in this section, we first simulate in non-white noise environment. According to the above description, we use white noise to generate colored noise through a first-order linear system [22]. The formula is described as follow:
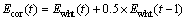 (26)
(26)
In which is white noise and
is white noise and  indicates colored noise.
indicates colored noise.
Firstly, we perform simulation verification on the preprocessing process of the observation data Uout(t) based on the wavelet denoising algorithm to illustrate the effectiveness of the wavelet denoising algorithm for the suppression of colored noise.
Here, the colored noise mentioned above is added to the observation value Uout(t), and the denoising preprocessing based on the wavelet algorithm is performed. The result is shown in Figure 11.
It can be seen from Figure 11 that a simple denoising preprocessing of the original signal can effectively suppress colored noise.
Secondly, we further verify the effectiveness of the proposed SOC estimation algorithm for SOC estimation under conditions of weak colored noise. Figure 12 shows the pre-processed voltage and current signals with weak colored noise.
Furthermore, we use the preprocessed data with weak colored noise in Figure 12 to verify the proposed SOC estimation method proposed in this paper. The results are shown in Figure 13.
It can be seen from the simulation results in Figure 13 that for the signal containing colored noise, we first perform simple preprocessing to reduce its color, and then use the AR-EKF algorithm proposed in this work to estimate the SOC. The estimation result is more accurate which can meet engineering requirements. This also validates the conclusions in Ref. [21].
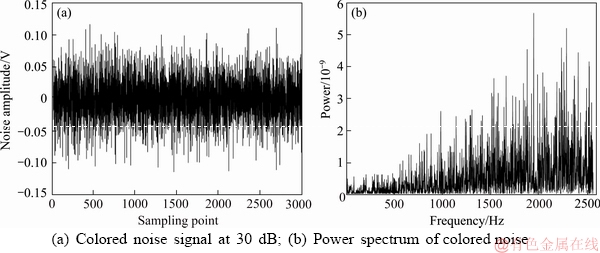
Figure 10 Colored noise signal and its power spectrum:
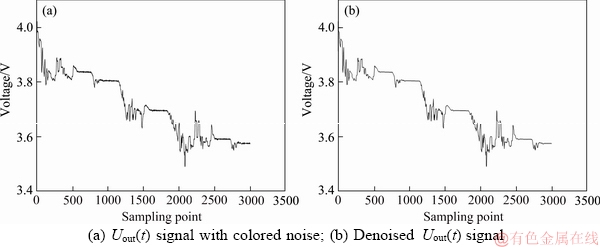
Figure11 Preprocessed simulation results for colored noise signals:

Figure 12 Pre-processed voltage and current signals with weak colored noise:
4.3.2 White noise
The above simulations are validated using ideal data without noise and real data with colored noise. From the simulation results, the AR-EKF- based SOC estimation method proposed in this work can obtain the estimation accuracy that meets the engineering requirements. Here, the estimation accuracy of the algorithm is further verified under a large white noise environment and without denoising processing. Here we plan to add a certain amount of white noise to the current signal I(t) and the external voltage signal Uout(t) respectively, and use the signal with white noise to verify the algorithm.
Simulation results using the above noise- containing are shown in Figure 15. In Figure 15(b), the SOC estimation error increases due to the presence of noise. It shows that the AR-EKF algorithm proposed in this work is not ideal for noise suppression. However, since the AR-EKF algorithm proposed in this paper has a closed-loop correction structure, it does not have the same problem as the data-driven SOC algorithm represented by the current integral method, which cannot eliminate the accumulated error. The simulation results also reflect that, for the proposed AR-EKF based SOC estimation algorithm, although there is no problem that cumulative error continues to increase with noise, the noise is fully reflected in the SOC estimation error and the data denoising is very necessary before SOC estimation.

Figure 13 SOC estimation verification result based on AR-EKF algorithm under weak colored noise:

Figure 14 Current I(t) and external voltage Uout(t) added noise:

Figure 15 Comparing results when data added noise:
4.4 Experimental verification
In this section, we further perform algorithm verification based on battery experiments. First, we collect a series of current signals from real electric vehicles as the discharge load current for the equipment of battery experiments in order to make battery discharge following the current signals.And through the battery experiment equipment, we can measure the corresponding external voltage signal Uout and real SOC data. The load current signal and external voltage signal are shown in Figure 16, and the verification results are shown in Figure 17.
It can be seen from the experimental verification results in Figure 17 that the deviation between the experimental result and the estimation result of the SOC estimation method based on AR-EKF proposed in this paper is small, and it is basically maintained within the range of ±1.5% to meet the engineering requirements.
5 Conclusions
This paper presents a data-driven EKF-based approach for battery SOC estimation of electric vehicles. The core idea of new method is effectively combining the data-driven SOC estimation method with the model-based SOC estimation method. It can avoid the problem that the data-driven SOC algorithm cannot eliminate the accumulated error, and improve the drawback of serious dependence on model accuracy of the model-based SOC estimation method. It is more suitable for the SOC estimation of the full life cycle of a power battery that operates in a complex and ever-changing environment such as an EV. The AR model-based data-driven modeling analysis is adopted to avoid the model inaccuracy caused by the poor battery consistency and to meet the time-varying characteristics of the impedance of the battery impedance, so that the algorithm has good dynamic characteristics. Since the main idea in this paper is based on the EKF-based SOC estimation method, it has the ability of closed-loop correction for the SOC, and thus has the advantages of fast convergence and no cumulative error. The experimental results illustrate that new method has good validity and practicability on SOC estimation of power battery using in EV.
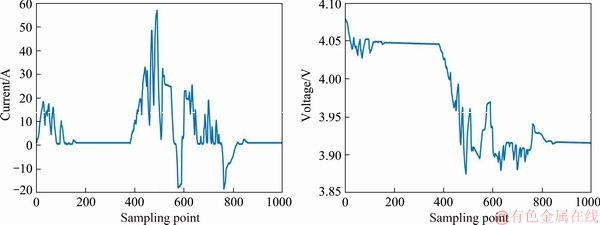
Figure 16 Load current signal I(t) (a) and corresponding external voltage signal Uout(t)

Figure 17 Comparing results with battery experiments:
References
[1] BABA A, ADACHI S. SOC Estimation of HEV/EV battery using series Kalman filter [J]. Electrical engineering in Japan, 2014, 187(2): 53-62. DOI: 10.1002/ eej.22511.
[2] HU Zhi-kun, LIU Bin, LIN Yong. Adaptive square root unscented Kalman filter for SOC estimation of battery [J]. Electric Machines and Control, 2014, 18(4): 111-116. DOI: 10.3390/en10091345.
[3] RIVERA-BARRERA J, MU OZ-GALEANO N, SARMIENTO-MALDONADO H. SOC Estimation for lithium-ion batteries: Review and future challenges [J]. Electronics, 2017, 6(4): 102. DOI: 10.3390/ electronics6040102.
OZ-GALEANO N, SARMIENTO-MALDONADO H. SOC Estimation for lithium-ion batteries: Review and future challenges [J]. Electronics, 2017, 6(4): 102. DOI: 10.3390/ electronics6040102.
[4] XU Jun, LIU Bing-he, WANG Xin-yi. Computational model of 18650 lithium-ion battery with coupled strain rate and SOC dependencies [J]. Applied Energy, 2016, 172: 180-189. DOI: 10.1016/j.apenergy.2016.03.108 .
[5] CHENG K W E, DIVAKAR B P, WU Hong-jie, DING Kai. Battery-management system (BMS) and SOC development for electrical vehicles [J]. IEEE Transactions on Vehicular Technology, 2011, 60(1): 76-88. DOI: 10.1109/ TVT.2010.2089647.
[6] PANDAY A, BANSAL H O, SRINIVASAN P. Thermoelectric modeling and online SOC estimation of Li-ion battery for plug-in hybrid electric vehicles [J]. Modelling and Simulation in Engineering, 2016, 2016: 1. DOI: 10.1155/2016/2353521.
[7] WANG Chuan-xin. SOC estimation algorithm for Li-ion battery in electric or hybrid vehicles [J]. International Journal of Electric and Hybrid Vehicles, 2016, 8(1): 61-77. DOI: 10.1504/IJEHV.2016.076962.
[8] PASCHERO M, STORTI G L, RIZZI A. A novel mechanical analogy-based battery model for SoC estimation using a multicell EKF [J]. IEEE Transactions on Sustainable Energy, 2016, 7(4): 1695-1702. DOI: 10.1109/TSTE.2016.2574755.
[9] ZHONG Fu-li, LI Hui, ZHONG Shou-ming, ZHONG Qi-shui, CHUN Yin. An SOC estimation approach based on adaptive sliding mode observer and fractional order equivalent circuit model for lithium-ion batteries [J]. Communications in Nonlinear Science and Numerical, 2015, 24(1-3): 127-144. DOI: 10.1016/j.cnsns.2014.12.015.
[10] MIAO Zhi-xin, XU Ling, DISFANI V R, FAN Ling-ling. An SOC-based battery management system for microgrids [J]. IEEE Transactions on Smart Grid, 2014, 5(2): 966-973. DOI: 10.1109/TSG.2013.2279638.
[11] TABORELLI C, ONORI S, MAES S,SVEUM P, AL-HALLAJ S, AL-KHAYAT N. Advanced battery management system design for SOC/SOH estimation for e-bikes applications [J]. International Journal of Powertrains, 2016, 5(4): 325-57. DOI: 10.1504/IJPT.2016.081795.
[12] ARUN K S, HUANG T S, BLOSTEIN S D. Least-squares fitting of two 3-D point sets [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1987 (5): 698-700. DOI: /10.1109/TPAMI.1987.4767965.
[13] GILLARD J. Circular and linear regression: Fitting circles and lines by least squares [J]. Journal of the Royal Statistical Society Series A-Statistics in Society, 2011, 174(3): 843-843. DOI: 10.1111/j.1467-985X.2011.00709_4.x.
[14] LI Ge-chen, GU Yan-lei. SOC of lithium-ion rechargeable battery predicted by electrochemical impedance spectroscopy [J]. Chinese Journal of Power Sources, 2008, 32(9): 599-602. (in Chinese)
[15] CHARKHGARD M, FARROKHI M. State-of-charge estimation for lithium-ion batteries using neural networks and EKF [J]. IEEE Transactions on Industrial Electronics, 2010, 57(12): 4178-4187. DOI: 10.1109/TIE.2010.2043035.
[16] GAUVAIN J L, LEE C H. Maximum a posteriori estimation for multivariate Gaussian mixture observations of Markov Chains [J]. IEEE Transactions on Speech and Audio Processing, 1994, 2(1): 291-298. DOI: 10.1109/89.279278.
[17] KRONE T, ALBERS C J, TIMMERMAN M E. A comparative simulation study of AR (1) estimators in short time series [J]. Quality & Quantity, 2017, 51(1): 1-21. DOI: 10.1007/s11135-015-0290-1.
[18] CHEN Jin-guang, MA Li-li. Error performance analysis of kalman filtering algorithm for non-Gaussian system [J]. Electronics Optics & Control, 2010, 17(9): 30-33. (in Chinese)
[19] TEWFIK L. Optimal tests in AR (m) time series model [J]. Communications in Statistics-Simulation and Computation, 2017, 46(2): 1583-1610. DOI: 10.1080/03610918.2015. 1009999.
[20] SU Wei-xing; ZHU Yun-long; LIU Fang, HU Kun-yuan. On-line outlier and change point detection for time series [J]. Journal of Central South University, 2013, 20(1):114-122. DOI: 10.1007/s11771-013-1466-2.
[21] HE Hong-wen, QIN Hong-zhou, SUN Xiao-kun, SHUI Yuan-peng. Comparison study on the battery SoC estimation with EKF and UKF algorithms [J]. Energies, 2013, 6(10): 5088-5100. DOI: 10.3390/en6105088.
[22] CUI Xian-qiang. Study on extension and application of adaptive robust foltering theory for controlling influence of colored noise in Kinematic Positioning [D]. Chang’an University, 2012. (in Chinese)
(Edited by FANG Jing-hua)
中文导读
基于数据驱动EKF算法的电动汽车及插电式混合动力汽车动力电池SOC估计
摘要:电池荷电状态(SOC)估计一直是动力电池和新能源汽车(含电动汽车(EV)、插电式电动汽车(PDEV)等)领域的研究热点。本文针对传统EKF(扩展卡尔曼滤波)算法对于动力电池模型精确性要求与全生命周期内的动态性要求之间的矛盾问题,提出了一种基于数据驱动EKF算法的SOC估计方法。该方法的创新之处在于:数据驱动的EKF动力电池SOC估计可以在动力电池内部参数未知的情况下,利用可观测的端电压和电流数据,实现动力电池SOC的在线准确估计。通过将基于数据的SOC估算方法与基于模型的SOC估计算法有效结合,有效避免了传统基于数据的SOC估计算法的累积误差问题以及基于模型的SOC估计算法对于电池模型精度的依赖性,使其更加适用于环境复杂多变 (例如EV和PHEV)的动力电池全生命周期SOC估算。实验结果表明,本文所提出的基于数据驱动的EKF动力电池SOC估计算法具有更好的鲁棒性和实用性。
关键词:电池荷电状态;扩展卡尔曼滤波;自回归模型;动力电池
Received date: 2018-09-13; Accepted date: 2019-02-17
Corresponding author: SU Wei-xing, PhD, Professor; Tel: +86-186-98011655; E-mail: 15900201597@163.com; ORCID: 0000-0003- 0911-6061

