一种稳健的二维自适应波束形成算法
陈涛,韩强强,刘鲁涛,隋莉莉
(哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨,150001)
摘要:针对已存在的各种二维capon 波束形成器稳健算法性能单一,只能对1种或2种影响波束形成算法性能的因素具有稳健性,缺乏对多种情况都具有稳健性的缺点,提出一种基于空间谱估计的二维稳健自适应波束形成方案。首先,提出一种新的二维解相关空间谱估计算法,该算法将二维角度估计问题用4个一维空间谱估代替,并采用修正的MUSIC算法实现解相干,然后利用得到的角度信息构造虚拟干扰,克服观察方向误差并展宽零陷。仿真结果表明:该算法结合了空间谱估计技术和自适应波束形成技术的优点,对期望信号导向矢量误差、干扰到达角失配及信号相关等都具有足够的稳健性。
关键词:二维自适应波束形成;稳健性;空间谱估计;修正的MUSIC;虚拟干扰
中图分类号:TN957.2 文献标志码:A 文章编号:1672-7207(2013)06-2339-07
A robust two-dimensional adaptive beamforming algorithm
CHEN Tao, HAN Qiangqiang, LIU Lutao, SUI Lili
(College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China)
Abstract: The existing two-dimensional robust adaptive beamforming algorithms only have simplex function, and the multifunctional robust beamforming algorithms are scarce. Aiming at all the cases which lead to performance degradation, an improved two-dimensional robust adaptive beamforming algorithm combined with spatial spectrum estimation technology was considered. Firstly, a new two-dimensional spatial spectrum estimation algorithm was proposed. This method utilized four one-dimensional spatial spectrum estimations to estimate the directions of the signals, and the modified MUSIC algorithm was used to estimate the coherent signals. Then the weight vector was calculated via virtual interferences constructed with the aid of angle information. Simulation results show that the algorithm simultaneously has the advantages of the adaptive beamforming technology and the spectrum estimation technology, and has sufficient robustness for steering vector error, interference angle of arrival mismatch and signal interrelation.
Key words: two-dimensional adaptive beamforming; robustness; spatial spectrum estimation; modified MUSIC; virtual interfaces
自适应波束形成技术广泛应用于雷达、声纳、通信等多种领域,它能在快速变化的信号环境中有效抑制从天线阵旁瓣进入的干扰,增强期望信号功率,并可针对环境给出不同的处理,一直是阵列信号处理的研究热点。在已经提出算法中,Capon波束形成器是其中一种最著名的算法。当协方差矩阵与导向适量准确已知时,Capon波束形成器是一种最优空间滤波器,可使阵列输出信干噪比(SINR)最大。实际中,对于有限的采样数,协方差矩阵不可能完全准确估计,观察方向误差和阵列校准误差也使得导向向量存在误差。无论两者哪个存在,都会使得Capon波束形成器性能降低。特别是当期望信号出现在训练快拍时,性能下降更加严重,且期望信号功率越大,性能下降越严重,即使是微小的失配也会引起性能急剧下降,甚至发生期望信号相消现象[1]。此外,自适应天线的研究往往基于理想的信号环境,而实际的干扰环境比较复杂,由于多径、色散或对方设置的有源干扰,经常会碰到信源为相干源的情形,若这时训练数据中包含期望信号成分,则即使没有其他误差,同样会引起期望信号相消,并且Capon波束形成器得到的自适应权值只能在干扰方向形成窄的零陷。若存在干扰位置的快速变化,将使得权值训练的据与权值应用的数据失配,干扰很可能移出零陷位置而不能有效对消,严重时,常规方法可能完全失效[2]。针对协方差矩阵失配和导向矢量误差,最为经典和广泛应用的方法是对角加载技术,它通过将加载量乘上单位阵加到采样协方差矩阵上代替原来的采样协方差矩阵。对对角加载量计算有很多算法,如最差情况性能最优化法(WCPO)[3-4]、HKB算法[5-6]、加权向量范数约束法(NCCB)[7]、按噪声功率选取加载电平等,都能计算出各自加载电平,用于提高波束形成器的性能。针对信号相关,若干扰方向已知,可用线性方差无失真响应(linearly constrained minimum variance,LCMV)算法对相干干扰方向强制约束为零。尽管LCMV算法通过干扰置零等措施改善自适应波束形成算法的抗干扰性能,但是,其中利用了干扰方向向量可以准确获得的假设,然而,这种假设在实际中并不完全被满足[8],当不能提前知道干扰源位置时,就需要先进性干扰源位置估计,才能使用LCMV算法,而且LCMV算法形成的零陷非常窄。一种有效的解决方法是加宽干扰零陷,使权值应用期间干扰始终处于零陷内。已有的零陷展宽方法有导数约束法[9]、协方差矩阵锥化(covariance matrix taper,CMT)[10-11]法。这2种方法有一个共同的缺陷:对于二维自适应天线阵,很难求得导数约束矩阵或CMT角度扩展矩阵。上述方法不能同时克服各种造成性能下降因素,且有些算法只能用于一维阵列信号处理,对于二维阵列信号处理,则受到限制。针对这种情况,本文作者提出一种结合空间谱估计的二维波束形成解决方案,能够同时克服信号相关、期望信号到达角失配、干扰方向零陷窄等问题。
1 二维解相干MUSIC算法
多重信号分类(multiple signal classification,MUSIC)算法是一种最为突出的空间谱估计技术。该算法通过对阵列输出数据协方差矩阵进行特征分解,得到与信号相对应的信号子空间和与之正交的噪声子空间,然后利用这2个子空间之间的正交性来估计信号的参数,其实现步骤如下。
首先,对采样数据协方差进行特征分解。
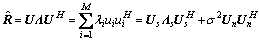 (1)
(1)
采样数据协方差矩阵的特征值按降序排列λ1>λ2>…>λN>λN+1=…=λM=σ2;Λ=diag[λ1,λ1,…,λM],Λs=diag[λ1,λ1,…,λN]。特征向量组成的酉矩阵U=[u1,u2,…,uM],大特征值对应的特征向量构成信号子空间Us=[u1,u2,…,uN],与噪声特征值λN+1=…=λM=σ2对应的特征向量构成噪声子空间UN=[uN+1,uN+2,…,uM]。此时,求得的噪声子空间与信号导向矢量相互正交。
然后,计算空间谱函数,进行谱峰搜索。定义空间谱函数:
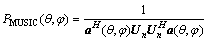 (2)
(2)
式中:θ为俯仰角;φ为方位角。搜索出空间谱函数的谱峰位置就可以给出N个信号的DOA。
MUSIC算法对不相关或弱相关信号具有很高的分辨率、估计精度及稳定性。对相关信号源,信号子空间扩散到噪声子空间,MUSIC算法将随信号源间的相关性(或相关系数)的增加,其性能逐渐降低,甚至失效[12]。为了对相干信号进行估计,需要除去相关性。本文提出一种新的二维解相干MUSIC算法。
假定一个信号到达角为(θ,φ),与x轴、y轴、z轴夹角分别为α,β和γ,如图1所示。则有:
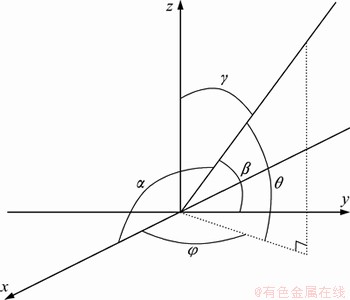
图1 信号入射模型
Fig. 1 Signal incident model
γ=π/2-θ (3)
cos θ×cos φ=cos α (4)
cos θ×cos φ=cos β (5)
由式(3)~(5)得:
sin2 γ=cos2 α+cos2 β (6)
对有N个信号源,若能估计出信号与各轴之间的夹角(α1,α2,…,αN),(β1,β2,…,βN),(γ1,γ2,…,γN),且将满足式(6)的αi,βj和γk为一组,则可以计算对应的方位角与俯仰角,如式(7)和(8)所示。
θ=π/2-γk (7)
φ=arctan(cos βi/cos αj) (8)
值得注意的是,通过式(8)计算的方位角还要进行修正,如下式所示:
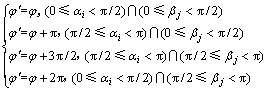 (9)
(9)
实际中,由于各种误差存在,即使是同一信号αi,βj和γk也不能使式(6)左右两边恰好相等,令
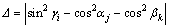 (i=1,2,…,N;
(i=1,2,…,N;
j=1,2,…,N;k=1,2,…,N) (10)
满足使得△足够小αi,βj和γk的为一组,然后,根据式(7)~(9)计算信号到达角。文献[13]分别在x轴、y轴、z轴放置一均匀线阵,求出入射信号的与各轴间的夹角,根据式(10)分组,这样可将二维MUSIC转换为三次一维MUSIC,并能利用均匀线阵的各种解相干算法来实现二维解相干,但它有严重的缺陷。
假定2个信号与x轴、y轴、z轴的夹角分别为(α1,β1,γ1)和(α2,β2,γ2),若这时α1和α2满足:
α1=π-α2 (11)
cos2 α1=cos2 α2 (12)
则按式(10)进行分组就会可能出现分组出错的情况。同理,在β1=π-β2时也会有同样的情形。
针对这一点,本文改进了天线阵排列方式,以克服分组出错的情况。天线阵采用图2所示的排列方式。
从图2可以看到:天线阵不仅在各坐标轴上放置了均匀线阵,同时在直线l上也放置了天线。其中,相邻阵元的间距d为信号波长的一半,直线l方程为:
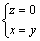 (13)
(13)
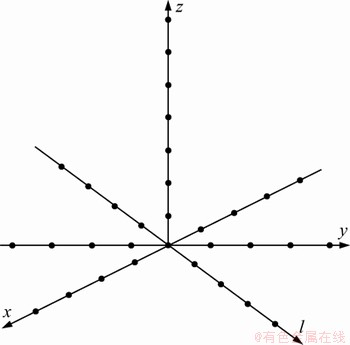
图2 天线阵结构
Fig. 2 Antenna array structure
如果测得信号与l夹角为υ,有
cos θ×cos (π/4-φ)=cos υ (14)
定义Λ为:
Λ=|cos υ-cos θ×cos (π/4-φ)| (15)
当利用式(10)分组,并通过式(7)~(9)计算对应的方位角、俯仰角以后,若在入射信号与l的夹角υi(i=1,2,…,N)中有使得Λ足够小的值,则说明分组正确;若没有,则说明分组错误,将该组去掉。
此外,为了对相干信号进行解相干,每个线阵采用修正MUSIC算法(Modified MUSIC,MMSIC)[14-15]。
对M元均匀线阵,假定有N个远场窄带平面波入射其上,第k次快拍的天线阵接受数据向量为
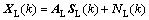 (16)
(16)
其中:XL(k)为M×1的天线阵接收数据向量;AL为M×N的阵列流型矩阵;SL(k)为N×1入射信号复振幅向量;NL(k)为M×1与信号源不相关的噪声向量。
数据协方差矩阵RL为
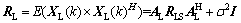 (17)
(17)
式中: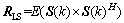 ;σ2为噪声功率;I为M阶单位阵。
;σ2为噪声功率;I为M阶单位阵。
取交换矩阵J为副对角线元素都为1,其余元素为0的M阶方阵,则J2=1,令
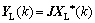 (18)
(18)
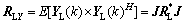 (19)
(19)
取
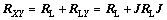 (20)
(20)
用RXY代替RL进行MUSIC算法,就可估计出相干信号源的到达角。
2 改进的LCMV算法
LCMV算法在Capon波束形成器基础上另加线性约束使固定方向增益为零。其数学模型为
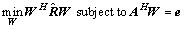 (21)
(21)
式中:W, ,A和e分别表示要求的加权向量、采样数据协方差矩阵、约束矩阵和响应向量。这是一个约束优化问题,可以利用拉格朗日乘子法求解。
,A和e分别表示要求的加权向量、采样数据协方差矩阵、约束矩阵和响应向量。这是一个约束优化问题,可以利用拉格朗日乘子法求解。
 (22)
(22)
若直接根据该公式进行权值计算,则形成的零陷很窄。为了展宽零陷,需要对LCMV算法进行改进。本文对LCMV算法改进的基本思想是协方差矩阵用虚拟干扰构造。协方差矩阵不用采样信号,而是利用估计出得DOA信息,构造虚拟信号,且这种虚拟信号在构造时只构造干扰成分,从而得到不包含期望信号成分的虚拟干扰,对期望信号DOA误差有足够的稳健性。构造出的协方差矩阵主要用于零陷展宽,克服传统LCMV算法零陷窄的缺陷。这样,计算的权值,既对期望信号失配具有稳健性,又具有宽零陷。
一方面,利用空间谱算法估计出的角度信息得出约束矩阵,通过式(21)中的约束条件AHW=e,期望信号无失真输出,并将干扰置零。
另一方面,对式(21)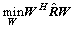 部分的
部分的 进行构
进行构
造。在存在干扰的情况下,自适应波束形成器能在干扰的方向上自动形成1个零陷。基于该原理,在干扰信号DOA不确定区域人为放置若干干扰源,只要人为放置的干扰源密度足够,不至于形成单个零陷,就能够在该区域形成1个宽的零陷。下面以来自(θ,φ)方向的干扰为例进行分析。
对于1个N元天线阵,(θ,φ)方向的响应向量为
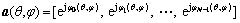 (23)
(23)
LCMV算法通过WHa(θ,φ)=0将其置零。这时,会在(θ,φ)方向上形成1个很窄的零陷。
假定θ的不确定性范围为(θ-△θ,θ+△θ),φ的不确定性范围为(φ-△φ,θ+△φ),在这个区域的放置K相互独立的干扰源。第i个干扰ui(t)的DOA为(θi,φi) 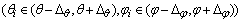 ,其对应的
,其对应的
 的响应向量为a(θi,φi),对应的协方差矩阵用Ri表示。
的响应向量为a(θi,φi),对应的协方差矩阵用Ri表示。
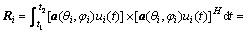
 (24)
(24)
式中: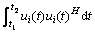 表示信号功率,设为p(θi,φi),有
表示信号功率,设为p(θi,φi),有
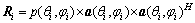 (25)
(25)
在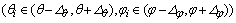 人为加入K个干扰,总的协方差矩阵为
人为加入K个干扰,总的协方差矩阵为
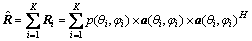 (26)
(26)
可使各个虚拟干扰强度一样均为1,即
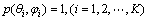 (27)
(27)
则
 (28)
(28)
对干扰信号DOA用同样的方法一方面进行置零,另一方面在其不确定区域构造虚拟协方差矩阵。总的协方差矩阵等于各方向上虚拟协方差矩阵之和。从式(28)可以看到:构造虚拟干扰并不是真的去构造一个具体形式的信号而是利用角度信息直接求出协方差 矩阵。
上面讨论的是如何进行虚拟协方差矩阵构造。若将式(28)构造的协方差矩阵直接用于权值计算,则在(θ,φ)方向形成1个宽零陷,但是不能控制主瓣宽度,这时,零陷展宽效果会很好,但主瓣很宽。为了在零陷效果与主瓣宽度之间进行调节,加入虚拟噪声部分。虚拟噪声的加入也是直接在已构造的协方差矩阵上处理。虚拟噪声假定为高斯白噪声。其协方差矩阵为对角元素相等的实对角阵,用RN表示,则
RN=αI (29)
其中:α和I分别为虚拟噪声功率和单位阵。这时,最终应用的LCMV算法的虚拟协方差矩阵R为
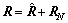 (30)
(30)
则最优权向量为
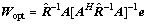 (31)
(31)
α可根据虚拟干扰的总功率确定和需要的信噪比确定。各个虚拟干扰功率都为1,则确定了虚拟干扰个数就能知道虚拟干扰总功率。信噪比要根据实际情况而定。所取信噪比越小,主瓣越宽,零陷展宽效果越好,反之,所取信噪比越大,主瓣越窄,零陷展宽效果越差。
3 仿真实验与结果分析
假定有3个远场窄带相干信号,信噪比为20 dB,所用快拍数为100。其中,1个期望信号DOA为(45°,120°),其余2个信号为相干干扰,DOA分别为(60°,30°)和(30°,270°)。
3.1 仿真1—空间谱估计算法仿真
图3~6所示分别为MUSIC算法x轴、y轴、z轴、直线l方向扫描谱。
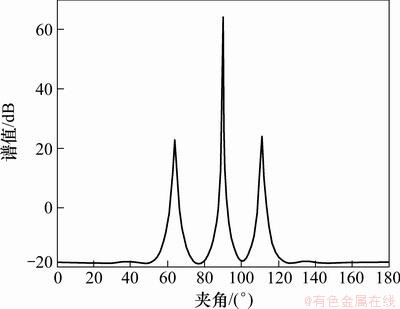
图3 x轴方向扫描图
Fig. 3 Scanning map of direction of x axis
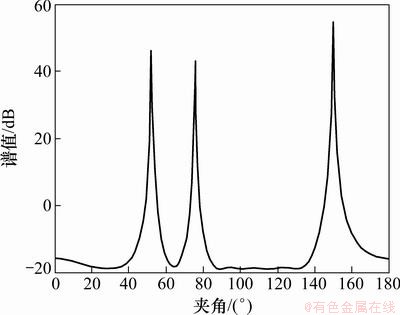
图4 y轴方向扫描图
Fig. 4 Scanning map of direction of y axis
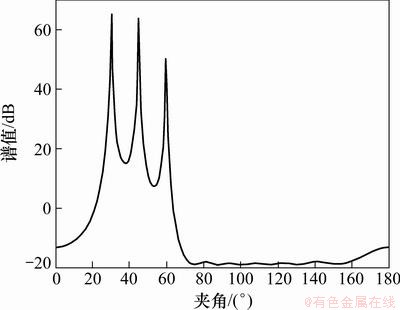
图5 z轴方向扫描图
Fig. 5 Scanning map of direction of z axis
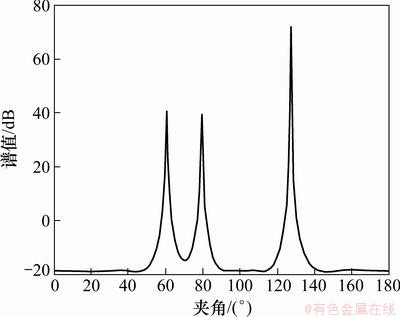
图6 直线l方向扫描谱
Fig. 6 Scanning map of direction of l axis
由估计出的值分组计算,得到信号DOA分别为 (45.1°,119.5°),(60.3°,30.2°)和(30.6°,270°),误差很小,能够比较准确估计信号的DOA。
3.2 仿真2—波束形成算法仿真
估计出角度信息以后,下面进行权值计算,将本文所提出的方法与静态LCMV权值进行对比,分别如图7~9所示。
从图7可以看到:在估计出期望信号DOA以后,即使存在估计误差,也能对期望信号无失真接收,静态LCMV加权与虚拟干扰LCMV加权几乎一样。而从图8和图9可以看出:由于对干扰DOA存在估计误差,可能会使得零线最低点位置并不刚好是干扰方向,但是,由于虚拟干扰LCMV法对零线进行了展宽,能够很好地抑制干扰;而静态LCMV零线很窄,不能够对干扰形成有效抑制。
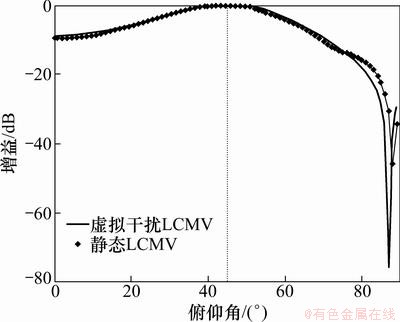
图7 方位角为120°对应俯仰角方向图对比
Fig. 7 Comparison of pattern in elevation angle when azimuth angle equals 20°
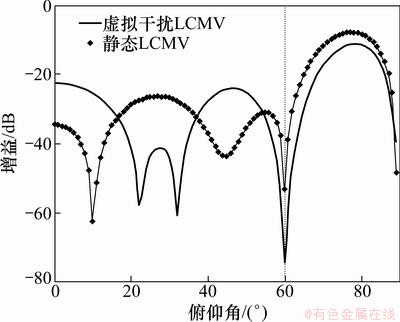
图8 方位角为30°对应俯仰角方向图对比
Fig. 8 Comparison of pattern in elevation angle when azimuth angle equals 30°
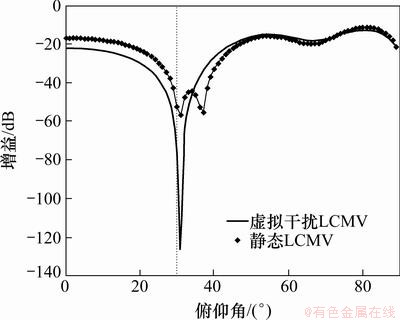
图9 方位角为270°对应俯仰角方向图对比
Fig. 9 Comparison of pattern in elevation angle when azimuth angle equals 270°
4 结论
(1) 提出了一种基于空间谱估计技术的二维稳健自适应波束形成方案,并通过仿真验证了该方案的有效性。
(2) 本文提出的二维解相干MUSIC算法能够对空间入射的相干信号进行二维空间谱估计,克服了二维相干信号难以进行空间谱估计的缺点。
(3) 用虚拟干扰代替实际信号采样值既能够无失真地接收期望信号,又可在干扰方向成宽零陷,从而消除了期望信号到达角失配、干扰方向零陷窄等因素对波束形成器性能的影响。
参考文献:
[1] 鄢社峰, 马远良. 传感器阵列波束优化设计及应用[M]. 北京: 科学出版社, 2009: 163-193.
YAN Shefeng, MA Yuanliang. Sensor array beampattern optimization design and application[M]. Beijing: Science Press, 2009: 163-193.
[2] 王永良, 丁前军, 李荣峰. 自适应阵列处理[M]. 清华大学出版社, 2009: 291-320.
WANG Yongliang, DING Qianjun, LI Rongfeng. Adaptive array processing[M]. Beijing: Tsinghua University Press, 2009: 291-320.
[3] Lorenz R G, Boyd S R. Robust minimum variance beamforming[J]. IEEE Trans Signal Processing, 2005, 53(5): 1684-1696.
[4] Vorobyov S A, CHEN Haihua, Gershman A B. On the relationship between robust minimum variance beamformers with probabilistic and worst-case distortionless response constraints[J]. IEEE Transactions on Signal Processing, 2008, 56(11): 5719-5724.
[5] Hoerl A E, Kennard R W, Baldwin K F. Ridge regression: Some simulations[J]. Communication in Statistics: Theory and Methods, 1975, 53(3): 105-123.
[6] Yngve S, Richard A, Peter S. Automatic robust adaptive beamforming via ridge regression[J]. Signal Processing, 2008, 88: 33-49.
[7] DU Lin. Fully automatic computation of diagonal loading levels for robust adaptive beam forming[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 449-458.
[8] Frost O L. An algorithm for linearly constrained adaptive array processing[J]. Proceeding of the IEEE, 1972, 60(8): 926-935.
[9] 刘永旭, 杨小鹏, 龙腾. 基于导数约束的互谱降秩自适应波束形成[J]. 北京理工大学学报, 2011, 31(9): 1095-1099.
LIU Yongxu, YANG Xiaopeng, LONG Teng. Reduced rank cross-spectral metric adaptive beamforming based on derivative constraint[J]. Journal of Beijing Institute of Technology, 2011, 31(9): 1095-1099.
[10] Zatman M. Production of adaptive array troughs by dispersion synthesis[J]. Electronics Letters, 1995, 31(25): 2141-2142.
[11] Mailloux R J. Convariance matrix augmentation to produce adaptive array pattern troughs[J]. Electronics Letters, 1995, 31(10): 771-772.
[12] 刘康, 习友宝, 李智. 信号相关性与修正MUSIC算法二维波达方向估计[J]. 计算机应用, 2012, 32(2): 592-594.
LIU Kang, XI Youbao, LI Zhi. 2-D direction of arrival estimation based on signal correlation and modified MUSIC algorithm[J]. Journal of Computer Applications, 2012, 32(2): 592-594.
[13] 战金龙, 胡国平. 一种新的二维MUSIC算法的研究[J]. 通信学报, 2004, 25(4): 69-74.
ZHAN Jinlong, HU Guoping, A novel 2-D MUSIC algorithm[J]. Journal of China Institute of Communications, 2004, 25(4): 69-74.
[14] Kundu D. Modified MUSIC algorithm for estimating DOA of signals[J]. Signal Processing, 1996, 48(1): 85-89.
[15] 何子述, 黄振兴, 向敬成. 修正MUSIC算法对相关信号源的DOA估计性能[J]. 通信学报, 2000, 21(10): 14-17.
HE Zishu, HUANG Zhenxing, XIANG Jingcheng. The performance of DOA estimation for correlated signals by modified MUSIC algorithm[J]. Journal of China Institute of Communications, 2000, 21(10): 14-17.
(编辑 杨幼平)
收稿日期:2012-06-25;修回日期:2012-09-21
基金项目:中央高校基本科研业务费专项项目(HEUCF120802);国家自然科学基金资助项目(61201410)
通信作者:陈涛(1974-),男,辽宁铁岭人,博士,副教授,从事宽带信号检测、处理及识别研究;电话:18204604801; E-mail:chentao@hrbeu.edu.cn