DOI: 10.11817/j.issn.1672-7207.2020.09.012
考虑柔轮杯体变形的谐波传动空间共轭齿廓设计与分析
朱飞鸿1,杜雪松1,宋朝省1,朱才朝1,杨勇2,廖德林2
(1. 重庆大学 机械传动国家重点实验室,重庆,400044;
2. 深圳市大族精密传动科技有限公司,广东 深圳,518057)
摘要:提出一种精确描述凸轮波发生器谐波传动刚柔轮之间复杂空间变形的方法,该方法基于直母线假定考虑柔轮空间变形带来的中面曲线变化和柔轮齿空间方位变化等因素搭建谐波传动运动学模型。以椭圆凸轮为例,利用数值法计算柔轮空间共轭齿廓,研究柔轮杯体空间变形所产生的空间转角及其对啮合过程中的共轭区域、柔轮齿运动轨迹和齿面啮合迹线带来的特殊影响。研究结果表明:柔轮齿空间方位转角不可忽视,其中切向位移引起的转角变化更加剧烈,所得柔轮齿廓共轭区域显著增大,齿圈轴向各截面均无干涉且存在两点啮合,啮合接触状况更优。
关键词:空间共轭;空间齿廓;谐波传动;双圆弧;椭圆凸轮
中图分类号:TH132.43 文献标志码:A
文章编号:1672-7207(2020)09-2471-09
Design and analysis of space conjugate tooth profile of harmonic drive considering deformation of flexspline cup
ZHU Feihong1, DU Xuesong1, SONG Chaosheng1, ZHU Caichao1, YANG Yong2, LIAO Delin2
(1. State Key Laboratory of Mechanical Transmissions, Chongqing University, Chongqing 400044, China;
2. Shenzhen Han's Motion Technology Co. Ltd., Shenzhen 518057, China)
Abstract: A method for accurately describing the complex space deformation between circular spline(CS) and flexspline(FS) of harmonic drive(HD) with a cam wave generator was proposed. The method was based on the assumption of the straight bus, considering the variation of the mid-surface curve caused by the deformation of the FS and the spatial orientation change of the FS teeth, and the kinematics model of the HD was built. Taking the elliptical cam as an example, the space conjugate tooth profile of the FS was calculated by numerical method. The space rotation angle generated by the deformation of the flexspline cup and its conjugate area, the relative movement trail of FS and the contact path on FS tooth surface during the meshing process were studied. The results show that the azimuth rotation angle of the FS tooth considered in this paper cannot be ignored, and the change of the rotation angle caused by the tangential displacement is more severe. The conjugated region obtained is significantly increased, and the cross-section of the FS has no interference and has two-point meshing, and the meshing contact condition is better.
Key words: space conjugate; space tooth profile; harmonic drive; double-circular-arc tooth profile; elliptical cam
谐波齿轮传动具有结构紧凑、减速比大、传动精度高等优点,广泛应用于航空航天、卫星通信和工业机器人等领域。在谐波传动中,柔轮发生的弹性锥度变形具有空间特征,尤其是工业机器人所使用的短筒谐波减速器将具有更明显的空间变形,因此,要获得良好的啮合特性,刚轮与柔轮需按空间共轭齿廓进行设计。目前的谐波传动齿形设计多以平面共轭齿形代替空间齿廓,或者虽然进行了空间齿廓设计但采用了较多假设,这样设计的齿形将会导致较多的啮合干涉和尖点啮合,从而产生不利于传动的齿面磨损,因此,有必要基于柔轮空间锥度变形建立更精确的谐波传动运动学模型,开展柔轮空间共轭齿廓设计研究。国内外学者对谐波传动结构设计分析[1-5]、啮合理论及运动学[6-7]、齿形研究[8-10],侧隙及啮合力分布[11-12],动态性能和控制[13]等领域开展了大量研究。在谐波传动共轭齿廓设计和求解方面,杨勇等[14]提出了精确的椭圆凸轮波发生器平面谐波传动运动学方法,为零侧隙谐波传动平面共轭齿廓的求解提供了思路;DONG等[7]提出了考虑柔轮锥度变形的谐波传动运动学模型,指出由于柔轮的空间变形,刚柔轮共轭齿廓之一必须是空间齿廓,否则会导致不必要的干涉和变形;吴伟国等[15-16]提出采用具有倾斜角度的刚轮齿形与产生空间锥度变形的柔轮啮合,并通过实验验证该方法可提高谐波减速器的传动刚度,但没有考虑若刚轮采用空间齿廓在批量加工时的工艺性问题;刘邓辉等[17]考虑柔轮锥度变形特征造成柔轮各截面中面曲线的差异,将刚轮空间齿廓的设计转化为多个横截面内的平面齿廓设计,该方法柔轮采用平面齿形,刚轮为空间共轭齿廓;周祥祥等[18-19]将柔轮齿圈离散成许多个横截面,通过合理调节各截面柔轮齿廓的径向位置设计具有倾角的柔轮空间齿廓;陈晓霞[20]基于直母线假定较准确地分析了柔轮空间锥度变形特征,但并未建立其运动学模型求解空间共轭齿廓。综上所述,现有研究都将刚柔轮齿廓看成离散的一系列截面来设计共轭齿廓,部分学者考虑了柔轮锥度变形造成的各截面中面曲线的差异,但忽略了柔轮杯体的空间变形还会引起柔轮齿的空间转动,变形后的柔轮齿横截面将不再垂直于旋转轴。本文作者考虑柔轮空间变形带来的中面曲线变化和柔轮齿空间方位变化,建立更精确的谐波传动运动学模型,利用数值法求解柔轮空间共轭齿廓,研究柔轮杯体空间变形所产生的空间转角,以及该转角对啮合过程中的共轭区域、柔轮齿运动轨迹和齿面啮合迹线带来的特殊影响,以便为高精度谐波齿轮传动共轭齿廓的求解和优化提供指导。
1 建立空间共轭运动学模型
谐波传动中,柔轮变形取决于波发生器几何形状和柔轮受载状况,柔轮受载状况能显著影响杯体变形,但刚柔轮齿间载荷分布又取决于轮齿齿形,如果要考虑载荷施加对柔轮变形带来的影响,就要首先建立空载状态下的轮齿几何特征,然后加入载荷,分析其带来的影响,以此作为齿形修形依据。故本文在理想轻载状态下建立考虑柔轮壳体中面空间变形的运动学模型,主要假设如下[20]:
1) 柔轮中面是柔轮圆柱壳体的中面;柔轮中面曲线是柔轮中面与横截面的交线;
2) 柔轮杯体看作铰接在输出端刚性杯底圆盘周边的圆柱壳,柔轮齿看作刚体,随直母线绕杯底铰接点发生由径向位移w和切向位移v引起的2个转动;
3) 柔轮杯体变形后,任意截面中面曲线由平面圆变为空间曲线,该曲线由径向、切向和轴向位移确定,忽略轴向位移认为各中面曲线变形后仍在同一平面。
以刚轮固定、波发生器逆时针旋转输入、柔轮顺时针旋转输出的谐波传动为研究对象,考虑柔轮杯体变形,建立如图1所示坐标系统,用于描述柔轮、刚轮和波发生器之间的相对运动及柔轮中面上选定点的位移和空间转角。其中,以刚轮回转中心O2为原点建立刚轮固定坐标系S2{O-X2Y2Z2}。以波发生器回转中心O为原点建立波发生器动坐标系S{O-XYZ},X轴为波发生器长轴。柔轮齿动坐标系为S1{O1-X1Y1Z1},X1轴为柔轮轮齿对称线,原点为X1轴与柔轮中性层交点。为准确描述柔轮在波发生器作用下的空间变形特征,建立辅助坐标系Sa,Sb和Sc来描述变形过程中切向位移v、径向位移w以及法向转角μ带来的坐标轴方位变化。在初始位置,X1,X2和X三轴共线,坐标系S和S2重合,坐标系S1中O1点位于波发生器长轴顶点。图1中所示位置为波发生器相对于X2轴逆时针旋转φ2时,柔轮非变形端相对于X2轴顺时针旋转α,而变形端则顺时针旋转γ。图1中,φ为波发生器相对于柔轮输出端的转角。
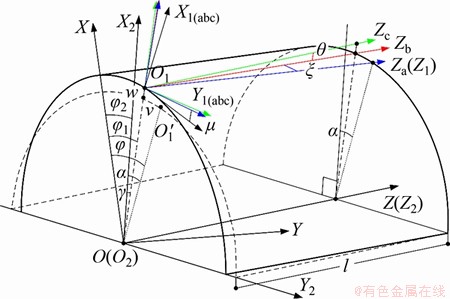
图1 谐波传动坐标系
Fig. 1 Coordinate systems of HD
波发生器迫使柔轮中面发生锥度变形,该变形过程中的位置移动及坐标轴方位变化由辅助坐标系Sa,Sb和Sc以及坐标系S1之间的平移和连续转动来描述:1) 柔轮变形使得啮合端O1点产生径向和切向位移从图1中O1′处移动到O1处,对应辅助坐标系Sc,Xc轴沿OO1方向,Zc轴平行于波发生器旋转轴Z轴(图2(a));2) 由径向位移w引起绕Yc轴的转角θ,辅助坐标系Sc旋转至坐标系Sb(图2(b));3) 由切向位移v引起辅助坐标系Sb绕Xc轴的转角ξ (Xc轴不是Sb坐标系的坐标轴),辅助坐标系Sb旋转至坐标系Sa(图2(c));4) 由柔轮变形引起绕Za轴的转角位移μ,辅助坐标系Sa旋转至坐标系S1(图2(d))。
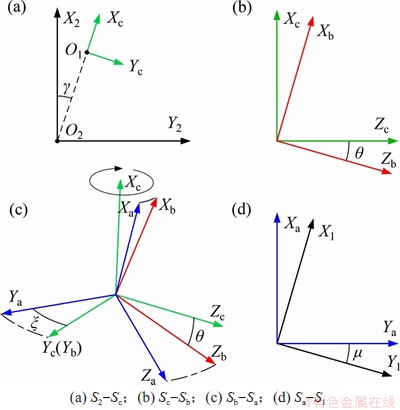
图2 谐波传动辅助坐标系
Fig. 2 Auxiliary coordinate systems of harmonic drive
为描述柔轮空间变形引起柔轮齿的方位变化,本文定义了由径向位移w引起绕Yc轴的转角θ和由切向位移v引起绕Xc轴的转角ξ,这2个空间转角对柔轮齿空间方位变化进行描述。所有运动参数选择以φ1为自变量表示,引入椭圆第二偏心率ε,可以推出2个空间转角的计算公式及其对φ1的求导表达式如下:
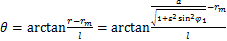 (1)
(1)
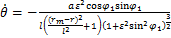 (2)
(2)
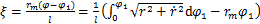 (3)
(3)
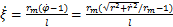 (4)
(4)
式中:rm为柔轮未变形时中性层半径;ω为变形系数;l表示设计主截面至杯底距离;a为柔轮中性层椭圆长轴;b为柔轮中性层椭圆短轴;Zf为柔轮齿数;Zc为刚轮齿数。
上述各式中的极径OO1长度r、转角位移μ、波发生器相对于柔轮输出端转角φ、波发生器相对于刚轮转角φ2和柔轮啮合端旋转角度γ的计算式及其对φ1的求导表达式参见文献[14]。
2 求解共轭齿廓
图1和图2所示的坐标系S2到S1的坐标变换矩阵如下:
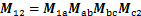 (5)
(5)
其中: ;
; ;
; ;
;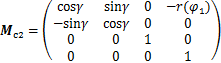 。
。
同理易得底矢变换矩阵W12。根据齿轮啮合原理,两齿面在接触点处必须满足以下啮合方程:
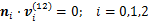 (6)
(6)
式中:ni为接触点的单位公法矢;vi(12)为接触点的相对运动速度矢量。
在S1坐标系中考虑式(6),代入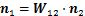 和
和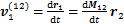 ,可将式(6)转化为
,可将式(6)转化为
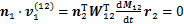 (7)
(7)
将刚轮齿廓曲线表示为以弧长s为参数的方程,对于齿廓曲线上每一点,都对应1个参数值si。将每一个弧长si(i=1,2,…,s)所对应齿廓曲线点的矢径r2和法向量n2代入式(7),得出该点发生共轭运动时的角φ1,记为φ1i(i=1,2,…,s)。根据每个φ1i确定对应M12中各元素值,得出相应的坐标变换矩阵M12i,代入下式,即可得出与刚轮齿廓共轭的柔轮理论齿廓。
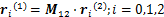 (8)
(8)
3 实例分析
以1款双圆弧谐波减速器为例,波发生器为标准椭圆凸轮,刚轮轮齿坐标系和公切线式双圆弧刚轮齿廓如图3所示。该减速器柔轮齿数Zf=160,刚轮齿数Zc=162,模数m=0.4,齿宽B=12 mm,波发生器径向变形系数ω0=1.0,全齿高h=1.7m=0.68 mm,齿顶高ha=0.8m=0.32 mm,齿根高hf=0.9m=0.36 mm,柔轮齿圈上齿形设计主截面至杯底的距离l=20 mm。刚轮具体参数如表1所示。
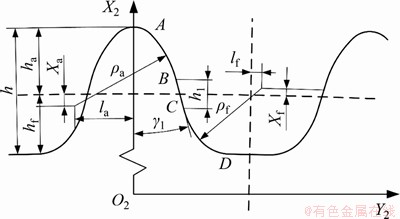
图3 刚轮双圆弧齿廓及刚轮坐标系
Fig. 3 DCTP and coordinate of a circular spline tooth
表1 刚轮齿廓参数
Table 1 Circular spline tooth profile parameters

在刚轮坐标系S2中,柔轮齿圈各截面用不同的Z坐标值zi来表征,根据直母线假设变形后柔轮各截面的径向变形系数ωi(i=1,2,…,c)可由下式来描述:
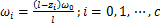 (9)
(9)
式中:l为设计主截面至杯底距离;zi为刚轮坐标系中各截面坐标值;ω0为波发生器径向变形系数。
式(9)中c为柔轮齿圈部分所选取的截面的个数,zi∈[2,-10]。将柔轮齿圈部分沿着旋转轴均分为25个横截面来表示(c=25),从第1到第25个横截面分别对应z=2,1.5,1,…,-10,齿形设计主截面的z=0。
对于其中的任意一个截面,径向变形系数ωi可由式(9)求得,空间转角θ和ξ以及它们对φ1的导数可由式(1)~(4)求得;将以弧长表示的刚轮齿廓上一系列齿廓曲线点所对应的矢径r2和法向量n2代入式(7),得出该点发生共轭运动时柔轮轮齿坐标原点的矢径OO1与波发生器长轴X轴间的夹角φ1,整个刚轮齿面的所有25个齿廓所求解的φ1构成该齿面的共轭区域,共轭区域由2部分组成分别称为共轭区域一和共轭区域二,如图4所示。
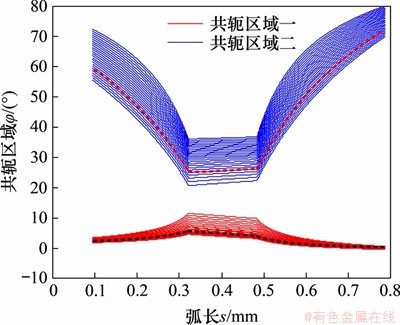
图4 空间齿廓共轭区域比较
Fig. 4 Comparison of conjugate existent domain of spatial tooth profiles
图4中加粗虚线部分表示没有考虑柔轮空间锥度变形的平面谐波啮合理论所求解的本例刚轮齿形对应的2个共轭区域,其中黑色虚线表示共轭区域一,红色虚线表示共轭区域二。由图4可得平面谐波啮合理论所求解的共轭区域一角度区间为[-0.461 8°,4.923°],共轭区域二角度区间为[24.92°,71.66°];而由本文的算法求得的空间齿廓共轭区域一和二所覆盖的角度区间为[-0.473 8°,11.44°]和[20.60°,79.94°]。相比平面谐波啮合理论本文算法共轭区域一的最小角度偏移量和最大角度偏移量分别为0.012°和6.517°,共轭区域二的角度偏移量分别为4.326°和8.287°。用偏移角度和共轭区间大小之比作为共轭区域扩展量的评估参数,则在共轭区域一中最小角度扩展量较小,为0.222 8%,最大角度扩展量为原共轭区间的1.21倍;在共轭区域二中最小角度扩展量为9.255%,最大角度扩展量为17.73%。由于最后计算得到的共轭齿廓受共轭区域一影响较大,以上分析表明本文算法计算所得共轭区域一是平面谐波啮合理论的2.21倍,显著增大了齿形的共轭区域,将使参与共轭啮合的轮齿数目更多,对提高双圆弧谐波减速器传动精度和扭转刚度、减少轮齿磨损、提高保精度寿命意义重大。
在式(8)中代入由共轭区域求得的坐标变换矩阵M12i,即可得出与刚轮齿廓共轭的柔轮理论齿廓。由于存在2个共轭区域,刚轮每个截面都对应着2个柔轮齿廓。图5所示为设计截面上与刚轮齿形共轭的柔轮齿廓,2个齿廓相互分离互不交叉,但它们中只有1个是可行的。图中黑色柔轮齿廓与平面谐波啮合理论共轭区域一对应,选择该齿廓为可行齿廓;红色齿廓曲线是柔轮齿在远离凸轮长轴的情况下求解得到的,该齿廓曲线本身存在自相交和折叠,而且在柔轮齿坐标系S1中齿廓x坐标较大,直接作为柔轮齿廓将导致较大的啮合干涉。
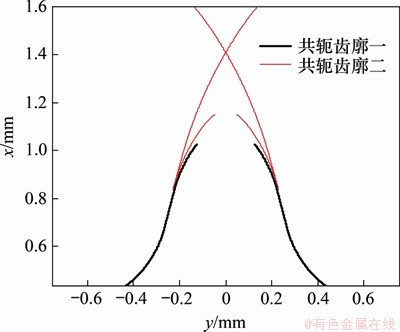
图5 柔轮平面共轭齿廓
Fig. 5 Flat flexspline conjugated tooth profiles
因此,对于刚轮齿圈每个截面,都可以采用相同的方法得到与之共轭的柔轮齿廓(如图6所示)。同样地,取与共轭区域一相对应的红色齿廓作为柔轮的空间齿廓,图7所示为该共轭齿廓的正视图。由本文模型得到的各截面柔轮空间共轭齿廓不仅考虑了不同截面中面曲线的变化,而且考虑了齿廓曲线所在平面发生的空间转动。转动角度由本文的精确空间共轭算法进行计算。
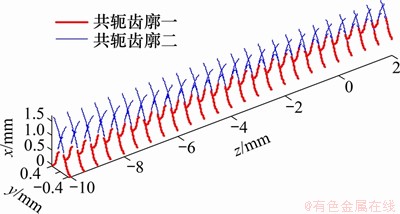
图6 柔轮空间共轭齿廓
Fig. 6 Spatial flexspline conjugated tooth profiles
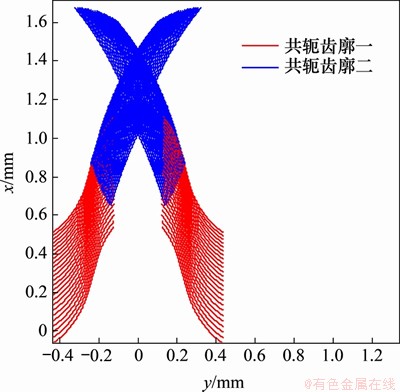
图7 柔轮空间共轭齿廓
Fig. 7 Spatial flexspline conjugated tooth profiles
随着波发生器的转动,柔轮变形过程中齿圈各截面柔轮齿产生的空间转角变化曲线分别如图8和图9所示,其中,图8所示为空间转角θ随极角φ1的变化规律,图9所示为空间转角ξ随极角φ1的变化规律;θ和ξ两角度的变化周期为π,用不同的颜色、线形来表示柔轮齿圈沿Z轴各个截面的空间转角变化规律,每根曲线之间的z坐标之差为2 mm。图8和图9中,黑色虚线表示设计截面,绿色虚线表示靠近开口端外侧齿圈截面,黑色实线表示靠近输出端内侧截面。从图8和图9可见:空间转角θ波动幅值较大,变化曲线关于180°轴对称,均值为1.083°,在n·π/2处出现极值,最大值出现在开口端θmax=1.228°,相比设计截面极值增大了7.16%,相比靠近输出端内侧截面极值增大了8.29%;切向位移v引起的转角ξ幅值较小,波动曲线关于180°轴反对称,均值为0°,在(2n+1)·π/4处出现极值,最大值出现在开口端ξmax=0.864 4°,相比设计截面极值增大了1.5倍,相比靠近输出端内侧截面极值增大了1.67倍;柔轮齿圈各截面上2个空间角度均产生了较大的变化,相比空间转角θ,转角ξ变化更加剧烈。该曲线变化规律与文献[20]中径向位移w、切向位移v的变化规律相吻合。
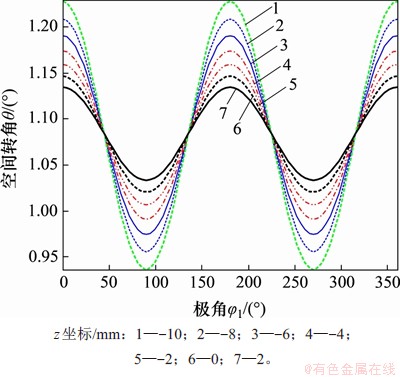
图8 柔轮齿圈各截面θ角位移曲线
Fig. 8 Node angular displacement θ on each section of flexspline
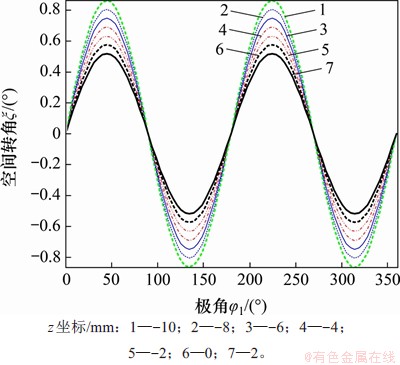
图9 柔轮齿圈各截面ξ角位移曲线
Fig. 9 Node angular displacement ξ on each section of flexspline
随着波发生器的转动,通过循环增加波发生器的转角,对各截面柔轮齿廓坐标点进行坐标变换来仿真柔轮齿和刚轮齿的相对运动状态。在波发生器旋转0°~360°的过程中,基于本文提出的空间共轭运动学模型的柔轮轮齿相对于刚轮齿槽的运动轨迹如图10~12所示。图10~12中红色曲线表示柔轮齿坐标系原点O1的运动轨迹在XY平面的投影,波发生器旋转1圈,柔轮转过2个齿。由图10~12可知:各齿圈截面的刚柔轮啮合轨迹均未发生干涉,且随距杯底轴向距离的增大,柔轮齿啮合运动轨迹的变形量也增大,与实际情况相符。
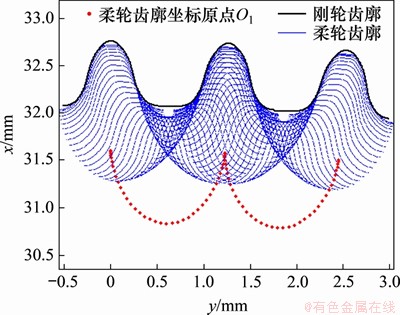
图10 Z=2截面柔轮齿运动轨迹
Fig. 10 Relative movement trail of Z=2 section
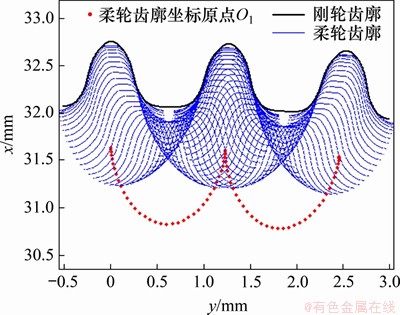
图11 Z=0截面柔轮齿运动轨迹
Fig. 11 Relative movement trail of Z=0 section
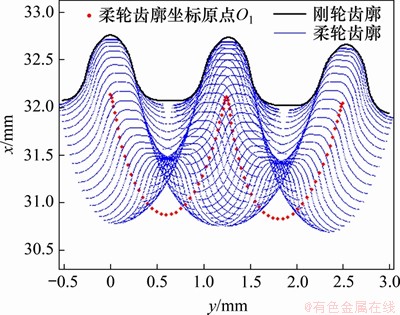
图12 Z=-10截面柔轮齿运动轨迹
Fig. 12 Relative movement trail of Z=-10 section
图13所示为本例柔轮空间齿面上的接触迹线分布情况,其中,将齿顶部分第1根以及齿根往上第5根标记为绿色,它们是在柔轮轮齿坐标原点矢径OO1与波发生器长轴X轴间的夹角φ1为2.291 8°时刚、柔轮齿面2个位置同时发生啮合接触形成的,这种现象被称为两点接触现象。从图13可以看出双圆弧谐波传动刚、柔轮齿的啮合从靠近齿根的位置开始,形成图13中φ1=0°时的接触迹线,齿宽方向有超过60%的齿面参与啮合,此时,波发生器长轴X轴与柔轮轮齿坐标原点矢径OO1间的夹角为0°;随着波发生器的转动,啮合迹线慢慢从齿根向上扩展,整个齿宽方向全部参与啮合,直到φ1=2.291 8°时齿顶部也开始出现啮合接触,在柔轮齿面出现2根接触迹线,形成两点接触;波发生器继续转动时,2根啮合接触迹线在齿面中部相遇,最终合成1根,慢慢沿齿宽方向退出啮合,当φ1=10.886 2°时完全退出啮合。图13中啮合迹线对应的共轭区域为[0°,10.886 2°],该共轭区域与前面本文算法计算的共轭区域一[-0.473 8°,11.44°]较吻合,与平面谐波啮合理论相比共轭区域增大。
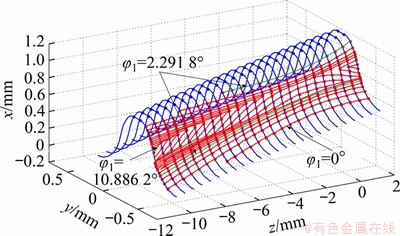
图13 柔轮齿面啮合接触迹线分布
Fig. 13 Contact path on flexspline tooth surface
4 结论
1) 考虑柔轮空间变形带来的中面曲线变化和柔轮齿空间方位变化等因素,提出一种精确描述刚柔轮之间复杂空间运动关系的运动学模型,能够便于求解计算空间精确共轭齿廓,所得空间齿廓具有更大的共轭啮合区域,这对提高谐波减速器承载能力和传动性能有重要意义。
2) 相比平面谐波啮合理论,本文算法所求解的2个共轭区域均显著扩大,对共轭齿廓具有显著影响的共轭区域一扩展了1.21倍,共轭区域二扩展了17.73%;有更多的齿对参与啮合,所得柔轮齿面啮合接触迹线可精确描述双圆弧齿形在空间共轭情况下的两点接触现象。
3) 本文所考虑的柔轮齿圈各截面上由径向位移和切向位移所引起的2个空间转角θ和ξ均发生了较大变化,不可忽视,其中,θmax=1.228°,与设计截面的θmax相比增加8.29%,ξmax=0.864 4°,与设计截面的ξmax相比增幅167%,与由径向位移w引起的转角θ相比,切向位移v引起的转角ξ变化更加剧烈。
参考文献:
[1] 董惠敏. 基于柔轮变形函数的谐波齿轮传动运动几何学及其啮合性能研究[D]. 大连: 大连理工大学机械工程学院, 2008: 15-25.
DONG Huimin. Study of kinematics and meshing characteristic of harmonic gear drives based on the deformation function of the flexspline[D]. Dalian: Dalian University of Techonology. School of Mechanical Engineering, 2008: 15-25.
[2] 范元勋, 王华坤. 齿啮输出谐波传动柔轮变形的研究[J]. 南京理工大学学报(自然科学版), 1996, 20(1): 38-42.
FAN Yuanxun, WANG Huakun. Study on the deformation of flexspline in the engagement output harmonic drive[J]. Journal of Nanjing University of Science and Technology(Nature Science), 1996, 20(1): 38-42.
[3] 王文静, 辛洪兵, 徐正兴. 谐波齿轮传动小长径比柔轮有限元应力分析[J]. 北京工商大学学报(自然科学版), 2007, 25(4): 26-29.
WANG Wenjing, XIN Hongbing, XU Zhengxing. Finite element analysis of flexspline in harmonic gear drive[J]. Journal of Beijing Technology and Business University(Natural Science Edition), 2007, 25(4): 26-29.
[4] 付军锋, 董海军, 沈允文. 谐波齿轮传动中柔轮应力的有限元分析[J]. 中国机械工程, 2007, 18(18): 2210-2214.
FU Junfeng, DONG Haijun, SHEN Yunwen. Stress analysis of the flexspline in harmonic gearing by using FEM[J]. China Mechanical Engineering, 2007, 18(18): 2210-2214.
[5] XU L, QIN L, ZHU C. Displacements for an electromechanical integrated electrostatic harmonic drive[J]. The Journal of Strain Analysis for Engineering Design, 2006, 41(2): 101-111.
[6] 辛洪兵. 研究谐波齿轮传动啮合原理的一种新方法[J]. 中国机械工程, 2002, 13(3): 181-183.
XIN Hongbing. A new method for research on engagement principle of harmonic drive[J]. China Mechanical Engineering, 2002, 13(3): 181-183.
[7] DONG Huimin, WANG Delun, TING K L. Kinematic effect of the compliant cup in harmonic drives[J]. Journal of Mechanical Design, 2011, 133(5): 051004.
[8] ISHIKAWA S, TAKIZAWA N. Wave gear drive having negative deflection meshing tooth profile: US, 7735396[P]. 2010-06-15.
[9] KAYABASI O, ERZINCANLI F. Shape optimization of tooth profile of a flexspline for a harmonic drive by finite element modelling[J]. Materials & Design, 2007, 28(2): 441-447.
[10] 辛洪兵. 双圆弧谐波齿轮传动基本齿廓设计[J]. 中国机械工程, 2011, 22(6): 656-662.
XIN Hongbing. Design for basic rack of harmonic drive with double-circular-arc tooth profile[J]. China Mechanical Engineering, 2011, 22(6): 656-662.
[11] 殷燕. 零侧隙渐开线谐波齿轮传动的参数优化设计及有限元分析[D]. 秦皇岛: 燕山大学机械工程学院, 2010: 33-60.
YIN Yan. Parameter optimization design and finite element analysis of zero-lateralspace involute harmonic gear driving[D]. Qinhuangdao: Yanshan University. School of Mechanical Engineering, 2010: 33-60.
[12] LI Shuting. Contact problem and numeric method of a planetary drive with small teeth number difference[J]. Mechanism and Machine Theory, 2008, 43(9): 1065-1086.
[13] XU Lizhong, ZHU Cuirong, QIN Lei. Parametric vibration for electromechanical integrated electrostatic harmonic drive[J]. Mechatronics, 2007, 17(1): 31-43.
[14] 杨勇, 王家序, 周青华, 等. 椭圆凸轮波发生器零侧隙谐波齿轮传动共轭齿廓精确求解[J]. 中南大学学报(自然科学版), 2017, 48(12): 3231-3238.
YANG Yong, WANG Jiaxu, ZHOU Qinghua, et al. Exact solution for conjugate profiles of zero backlash harmonic drives with elliptical cam wave generators[J]. Journal of Central South University(Science and Technology), 2017, 48(12): 3231-3238.
[15] 吴伟国, 于鹏飞, 侯月阳. 短筒柔轮谐波齿轮传动新设计新工艺与实验[J]. 哈尔滨工业大学学报, 2014, 46(1): 40-46.
WU Weiguo, YU Pengfei, HOU Yueyang. New design, new process of harmonic drive with short flexspline and its experiment[J]. Journal of Harbin Institute of Technology, 2014, 46(1): 40-46.
[16] 车鸿臣. 轮齿有倾角的短筒柔轮谐波传动优化设计及研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2017: 60-72.
CHE Hongchen. The optimization design and study of short flexpline harmonic drive with leaning teeth[D]. Harbin: Harbin Institute of Technology. School of Mechatronics Engineering, 2017: 60-72.
[17] 刘邓辉, 邢静忠, 陈晓霞. 渐开线谐波齿轮的空间齿廓设计及啮合特性分析[J]. 机械设计, 2016, 33(3): 24-29.
LIU Denghui, XING Jingzhong, CHEN Xiaoxia. Spatial tooth profile design and engagement analysis of harmonic gear with involute profile[J]. Journal of Machine Design, 2016, 33(3): 24-29.
[18] 周祥祥. 三维双圆弧齿廓谐波传动的齿形设计与分析[D]. 重庆: 重庆大学机械工程学院, 2016: 51-69.
ZHOU Xiangxiang. Three dimensional profile design and analysis of harmonic drive with double-circular-arc common-tangent tooth profile[D]. Chongqing: Chongqing University. College of Mechanical Engineering, 2016: 51-69.
[19] 袁攀. 基于齿条近似法的谐波齿轮传动空间齿廓设计与分析[D]. 重庆: 重庆大学机械工程学院, 2017: 43-61.
YUAN Pan. Spatial profile design and analysis of harmonic drive by rack approximation theory[D]. Chongqing: Chongqing University. College of Mechanical Engineering, 2017: 43-61.
[20] 陈晓霞. 基于侧隙评价的谐波齿轮圆弧齿廓设计及状态仿真研究[D]. 天津: 天津工业大学机械工程学院, 2012: 15-20.
CHEN Xiaoxia. Arc tooth profile design and simulation research of harmonic drive based on mesh backlash assessment[D]. Tianjin: Tianjin Polytechnic University. School of Mechanical Engineering, 2012: 15-20.
(编辑 杨幼平)
收稿日期: 2019 -11 -18; 修回日期: 2020 -04 -09
基金项目(Foundation item):广东省重点领域研发计划项目(2019B090917002);重庆市科委产业类重点研发项目(cstc2018jszx-cyztzxX0039);重庆市科委创新类重点研发项目(cstc2018jszx-cyzdX0056) (Project(2019B090917002) supported by the Research and Development Plans in Key Areas of Guangdong Province; Project(cstc2018jszx-cyztzxX0039) supported by the Key Research and Development Project of Technological Innovation and Application Demonstration Program of Chongging Municipality; Project(cstc2018jszx-cyzdX0056) supported by the Key Research and Development Project of Technological Innovation Program of Chongging Municipality)
通信作者:杜雪松,博士,副教授, 从事精密齿轮传动研究;E-mail:948203652@qq.com