J. Cent. South Univ. Technol. (2008) 15(s1): 155-157

DOI: 10.1007/s11771-008-336-9

Simulation of rheological behavior of asphalt mixture with lattice model

YANG Sheng-feng(杨圣枫), YANG Xin-hua(杨新华), CHEN Chuan-yao(陈传尧)

(School of Civil Engineering and Mechanics, Huazhong University of Science and Technology, Wuhan 430074, China)

Abstract: A three-dimensional (3D) lattice model for predicting the rheological behavior of asphalt mixtures was presented. In this model asphalt mixtures were described as a two-phase composite material consisting of asphalt sand and coarse aggregates distributed randomly. Asphalt sand was regarded as a viscoelastic material and aggregates as an elastic material. The rheological response of asphalt mixture subjected to different constant stresses was simulated. The calibrated overall creep strain shows a good approximation to experimental results.

Keywords: asphalt mixture; rheological behavior; lattice model; creep

1 Introduction

Asphalt mixture is a composite material of graded aggregates bound with asphalt. Mechanical properties of asphalt mixture are governed by the properties of asphalt, properties of aggregate and asphalt-aggregate interactions. Complex structure of asphalt mixture makes the numerical modeling of asphalt mixture very challenging. Numerical simulation is one of the most important methods to investigate mechanical properties of asphalt mixture. DAI and YOU^[1] used random elliptical aggregates to model the microstructure of asphalt mixture with the FE method. YOU^[2] and CHANG^[3] used the discrete element model to simulate the initiation and propagation of crack in asphalt mixture. These models are limited to two-dimension, so that interaction between adjacent aggregates can not be considered sufficiently. Recently, the lattice model was widely used for heterogeneous anisotropic materials such as asphalt mixture^[4-6]. Random distribution and content of aggregates can be taken into account in this model. To provide some guidelines for optimizing design of asphalt mixture, a 3D numerical model capable of simulating rheological behavior of asphalt mixture was developed.

2 Numerical model

2.1 3D random lattice model

Asphalt mixture can be described as two-phase composite material consisting of coarse aggregates and asphalt sand^[7-8]. Coarse aggregates are assumed as elastic material and asphalt sand is viscoelastic material described by the generalized Maxwell constitutive model. The model parameters are determined by experiments.

The 3D random lattice model of asphalt mixture was established after the following steps: First, a cube with size of 0.1 m×0.1 m×0.1 m was created. And then it was discretized into a number of cubic cells with the same size and shape. Finally two kinds of material properties were assigned to different cells randomly according to aggregate content. As shown in Fig.1, the viscoelastic property is assigned to the pink cells as asphalt sand, and the elastic property is assigned to the blue ones as aggregate. The FE model was developed by generating FE mesh in the lattice model. The assumption that each element in the model was isotropic was introduced here.

FE creep simulation was conducted on the established lattice model to predict rheological response of the asphalt mixture. All of the nodal displacements in the bottom layer and the nodal displacements in x and y directions in the top layer were constrained, and a constant stress was imposed on the top layer. The displacement of the top layer in z direction was recorded over a period of time. The overall axial strain was computed by dividing the displacement of the top layer with the initial height of the model.

2.2    Viscoelastic constitutive relationship of asphalt sand

Based on the principle of superposition, the stress-strain behavior of a linear isotropic viscoelastic material was defined using a hereditary integral formulation as follows:

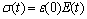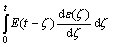+                         (1)

Fig.1 Random lattice model of asphalt mixture

where ε(t) and E(t) are axial strain and relaxation modulus.

  As a viscoelastic material, asphalt sand was described by the generalized Maxwell constitutive model as shown in Fig.2. In relaxation experiment, the applied step strain is

ε(t)=ε₀H(t)

where  ε₀ is constant strain, and .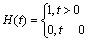

Substituting the step strain into Eqn.(1), it becomes

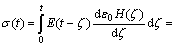
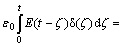
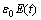
And E(t) can be expressed with a Prony series

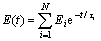                            (2)

where  τ_i=η_i/E_i; E_i, η_i and τ_i are spring constant, dashpot viscosity and relaxation time in the Maxwell model, respectively.

Fig.2 Generalized Maxwell model

Three-dimensional behavior can be formulated with uncoupled volumetric and deviatoric stress-strain relations.

                    (3)

where  σ_kk and ε_kk are volumetric stress and strain, respectively; S_ij and e_ij are deviatoric stress and strain, respectively; 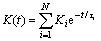 and 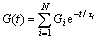 are volumetric and shear relaxation modulus, respectively; K_i=E_i/3(1- 2v); G_i = E_i/2(1+v).

The experimental data were fitted to Eqn.(2) by a non-linear least square fit and the parameters E_i, τ_i, N were obtained. Substituting E(t) into Eqn.(3), the three- dimensional constitutive relationship was established and incorporated into a subroutine de?ning material behavior in the finite element program.

Two types of experiments were performed in this work. Relaxation tests were conducted on asphalt sand samples to determine the viscoelastic parameters of the generalized Maxwell constitutive model. Creep tests were conducted on asphalt mixture to generate experimental data that could be compared with the FE analysis results.

The used asphalt sand consists of asphalt and fine aggregates passing sieve size 2.36 mm. As shown in Fig.3, when the mass fraction of asphalt is 0.06 in the asphalt sand, four-term Prony series is found to fit the experimental data well, and the fitting parameters are:

E₁=18.8 MPa, τ₁=5.9 s;

E₂=31.8 MPa, τ₂=34.7 s;

E₃=20.9 MPa, τ₃=206.3 s;

E₄=26.6 MPa, τ₄=5908.4 s.

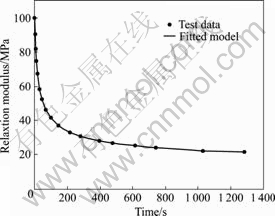
Fig.3 Relaxation modulus and fitted curve for asphalt sand

The modulus of limestone aggregate generally varies from 33 GPa to 48 GPa. 40 GPa is used for this study. Poisson’s ratios of 0.3 and 0.35 are used for the aggregate and asphalt sand respectively.

The volume fraction of coarse aggregates is fixed at 0.53 in the asphalt mixture. In the lattice model, the shape of aggregates is assumed be as cubic and their sizes are also the same as each other. In order to involve contributions of aggregate shape, size, and gradation, a calibration factor K is introduced in strain prediction. The factor is the ratio between the initial experiment strain and the prediction at an identical loading condition. K is found to be 0.112 when the loading stress is 0.05 MPa. The calibrated prediction is compared with the test data as shown in Fig.4. The predicted strain is very close to the experimental results when the loading time is shorter and the loading stress is lower. The predicted strain is obviously smaller than the experimental results for higher loading stress and longer loading time. The possible reason is that viscoplastic strain is neglected in the model.

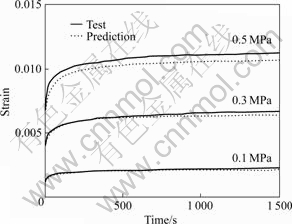
Fig.4 Predicted strain and measurement of asphalt mixture for different loading stress

1) The strain predicted by the 3D lattice model matches the measurement well for lower loading stress and shorter loading time, but the model slightly underpredicts the strain for higher loading stress and longer loading time because of neglecting viscoplastic strain.

2) The generalized Maxwell model can describe the viscoelastic behavior of the asphalt sand well. Relaxation test of asphalt sand is conducted to determine the material parameters in the Maxwell model, and creep test of asphalt mixture provides a comparison with the model prediction.

References

[1] DAI Q, YOU Z. Prediction of creep stiffness of asphalt mixture with micromechanical finite-element and discrete-element models [J]. Journal of Engineering Mechanics, 2007, 133(2): 163-173.

[2] YOU Z, BUTTLAR W G.Discrete element modeling to predict the modulus of asphalt concrete mixtures [J]. Journal of Materials in Civil Engineering, 2004, 16(2): 140-146.

[3] CHANG G K, MEEGODA J N. Micromechanical simulation of hot mixture asphalt [J]. ASCE Journal of Engineering Mechanics, 1997, 123(5): 495-503.

[4] BINGLIN L, TORQUATO S. N-point probability functions for a lattice model of heterogeneous media [J]. Physical review B, 1990, 42(7): 4453-4459.

[5] TORQUATO S. Random heterogeneous media: microstructure and improved bounds on effective properties [J]. Applied Mechanics Review, 1991, 44(2): 37-75.

[6] FENG Wei-gan, YANG Xin-hua, CHEN Chuan-yao. Analysis of effective macro-mechanical properties of heterogeneous elastic isotropic materials with normal distribution [J]. Journal of Mechanical Strength, 2008, 30(1): 132-136. (in Chinese)

[7] ABBAS A R, PAPAGIANNAKIS A T, MASAD E A. Linear and nonlinear viscoelastic analysis of the microstructure of asphalt concretes [J]. Journal of Materials in Civil Engineering, 2004, 16(2): 133-139.

[8] LI Y Q, METCALF J B. Two-step approach to prediction of asphalt concrete modulus from two-phase micromechanical models [J]. Journal of Materials in Civil Engineering, 2005, 17(4): 407-415.

(Edited by ZHAO Jun)

Foundation item: Project(10672063) supported by the National Natural Science Foundation of China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: YANG Xin-hua; Tel: +86-27-87540153; E-mail: yangxinh@263.net