DOI: 10.11817/j.ysxb.1004.0609.2021-35865

全尾砂胶凝材料配比正交试验及其充填体强度模型

吴  凡¹，高  谦¹，杨志强^{1, 2}

(1. 北京科技大学 土木与资源工程学院，北京 100083；

2. 金川集团股份有限公司，金昌 737100)

摘  要：为了确定超深铁矿胶结充填体强度模型，进行全尾砂胶凝材料配比的充填体强度正交试验，研究水泥熟料、脱硫石膏和工业芒硝对充填体强度性能的影响，并建立充填体强度预测模型。结果表明：充填体强度随水泥熟料添加量的增大而减小，随脱硫石膏和芒硝添加量的增大而增大。全尾砂胶凝材料最优配方：水泥熟料9%、脱硫石膏4%、芒硝1%。考虑井下作业时间，建立了养护龄期与其强度的双曲线函数关系，揭示随龄期增长强度先增加后趋于稳定的规律，为此提出极限抗压强度p₁和修正参数p₂的概念；采用1st Opt软件，极限抗压强度及修正参数与熟料添加量、石膏添加量及芒硝添加量呈多元非线性关系；综合胶凝材料添加量和养护龄期，建立充填体强度模型。模型预测误差小于6%，满足工程预测精度，可应用于全尾砂胶凝材料开发与强度预测。

关键词：胶凝材料；正交试验；数据可视化；配比优化；强度模型

文章编号：1004-0609(2021)-08-2269-10　　     中图分类号：TD853　　     文献标志码：A

引文格式：吴  凡, 高  谦, 杨志强. 全尾砂胶凝材料配比正交试验及其充填体强度模型[J]. 中国有色金属学报, 2021, 31(8): 2269-2278. DOI: 10.11817/j.ysxb.1004.0609.2021-35865

WU Fan, GAO Qian, YANG Zhi-qiang. Orthogonal experiment on ratio of whole tailings cementitious materials and strength model of filling body[J]. The Chinese Journal of Nonferrous Metals, 2021, 31(8): 2269-2278. DOI: 10.11817/j.ysxb.1004.0609.2021-35865

目前，随着社会高速发展，我国深部矿产资源开采已然趋于常态，高应力是诱发深部资源开采工程灾害的决定要素^[1-4]。充填采矿法由于在稳定深部采矿环境结构、控制地压及地表塌陷、保护自然环境和建立工业生态矿山等方面具有显著的作用，愈来愈多的国家要求矿山选择充填采矿法，充填料浆流动性能与凝结后的充填体强度是充填领域的两大核心，而矿山充填体强度直接影响采矿环境结构稳定性，是充填采矿设计的关键技术^[5-9]。

近年来，国外学者通过大量现场试验数据，建立了充填体强度模型^[10-12]，例如建立了水泥含量、孔隙率和水灰比对强度影响的Mitchell-Wong强度模型^[10]；建立了胶结剂体积含量、骨料颗粒间的自由距离和骨料表面积对强度影响的Swan强度模 型^[11]；建立了单轴抗压强度与水灰比的关系、黏聚力和单轴抗压强度的Arioglu强度模型^[12]。同时，国内专家学者对充填体强度模型也进行了大量深入研究工作，并取得了许多具有矿山实践的充填体强度模型的成果。付自国等^[13]建立了超细全尾砂胶结充填体关于体积浓度、水灰比和时间的三变量强度数学模型；聂亚林等^[14]建立了充填体强度与尾砂含水率之间的定量关系；徐淼斐等^[15]建立了充填体强度与波速指数函数预测模型；杨啸等^[16]建立了充填体强度与混合骨料的平均粒径、不均匀系数和料浆浓度的数学模型；曹帅等^[17]建立了充填体强度与充填间隔时间或填充次数的定量关系；兰文涛等^[18]使用高斯-牛顿算法，依据正交试验数据，建立了充填体强度与外加剂掺量、料浆浓度以及尾砂掺量的关系。吴疆宇等^[19]建立了充填体强度与骨架颗粒Talbol指数的关系。国内外研究表明，影响矿山充填体强度的因素较多，现有的强度模型往往适用于特定矿山，而养护时间与胶凝材料添加量作为影响充填体强度的重要因素，基于这两大影响因素的强度模型研究相对较少。

在矿山实际充填中，料浆浓度、胶砂比和充填骨料往往依据充填设计要求保持固定不变。基于此，本文作者以某超深矿山全尾砂胶凝材料配比正交试验为依据，通过直观分析、方差分析和数据可视化等手段，采用正交试验的效应分析方法^[20]，详细分析了水泥熟料添加量、脱硫石膏添加量和芒硝添加量的优化配合比，进一步建立了考虑时间效应的全尾砂充填胶凝材料的强度模型，为适用于不同作业龄期的矿山充填料浆配合比设计提供合理依据。

1  实验

1.1  试验材料

试验使用矿渣、水泥熟料(简称熟料)和脱硫石膏(简称石膏)作为胶凝材料。矿渣来自本溪某超深铁矿的水淬高炉矿渣，水泥熟料和脱硫石膏对矿渣起复合激发的作用。早强剂为工业芒硝，主要为对矿山充填体起到早强作用。骨料为该矿的全尾砂(简称尾砂)，为惰性材料。

试验原料的XRD谱如图1所示。由图1可见，矿渣在25°~35°具有明显的峰包，表明矿渣物相组成以玻璃态为主，同时发现少量矿物相钙铝黄长石 (Gehlenite)；熟料的主要矿物相为硅酸三钙(C₃S)，另外含有少量的铝酸三钙(C₃A)和硅酸三钙(C₂S)；石膏的主要矿物相为二水硫酸钙(CaSO₄·2H₂O)；尾砂的主要矿物相为石英(Quartz)、绿泥石(Chlorite)和闪石(Amphibole)。将胶凝材料、骨料进行X射线荧光光谱试验(XRF)分析与粒度分析，化学成分分析结果见表1所示，粒径分布结果如图2所示。

图1  试验原料XRD谱

Fig. 1  XRD patterns of raw materials

图2  试验原料粒径分布

Fig. 2  Particle size distribution of raw materials

表1  原料化学成分分析表

Table 1  Chemical composition of raw materials

1.2  试验方案

不同养护龄期充填体强度目标不同，为开发适用于不同作业时间的充填料浆，先在实验室进行了探索性试验。探索性试验中发现在胶砂比1:8且料浆质量浓度为65%时，料浆泌水率较低，流动性较好。固定试验料浆胶砂质量比为1:8，浓度为65%。为减少试验工作量，胶凝材料配比采用正交试验，确定三个考察因素：熟料添加量(因素A)、石膏添加量(因素B)和芒硝添加量(因素C)，每个因素各取3个水平，采用正交表L9(3⁴)，试验因素与水平见表2。熟料添加量、石膏添加量和芒硝添加量为熟料、石膏和芒硝在胶凝材料中的含量。

表2  胶凝材料配比试验因素与水平

Table 2  Factors and levels of orthogonal test for cementitious materials mix proportion

具体试验方法为：试件分为5大组，分别用于不同龄期抗压强度试验，每大组为9小组，每小组3个试块，共计135个70.7 mm×70.7 mm×70.7 mm立方体充填体试块。试块制作1 d后脱模，然后进行标准养护(湿度95%，温度20 ℃)，养护至规定龄期(3、7、14、28和56 d)后，参照水泥胶砂强度检验方法进行强度测试，抗压强度试验采用的是万能压力机WE-100。

不同养护龄期充填体试块材料配合比与抗压强度正交试验结果见表3，抗压强度与养护龄期的关系如图3。值得一提的是，在试验数据处理过程中，将各龄期实验结果离散性最大数值剔除后，求其抗压强度平均值。

由表3和图3可见，不同水平组合下的充填体抗压强度随养护时间发展一直处于增长状态，无明显的下降趋势。充填体的抗压强度增长率随养护时间的延长先增加后变缓，早期(3~7 d)增加较快，中期(8~28 d)增长变缓，后期(29~56 d)增加趋于0。7 d抗压强度就达到了56 d抗压强度的71.6%~82.4%，发展很快；之后，发展较为缓慢，28 d后基本趋于稳定。

图3  胶结充填体抗压强度与养护龄期的关系

Fig. 3  Relationship between strength and curing time of cement filling body

表3  胶结充填体试块材料配合比与试验结果

Table 3  Mix proportion and result of cement filling body

2  试验分析

2.1  直观分析

由表3可知，C3试块的1、3、7、14、28和56 d抗压强度在9组试验中均最大，此时熟料添加量A取水平1(9%)，石膏添加量B取水平3(4%)，芒硝添加量C取水平3(1%)，即充填体试块强度达到最大的组合为A1B3C3。按正交试验直观分析理论^[20]计算出各目标因素相同水平组充填体的抗压强度平均值及其极差，抗压强度平均值与各目标因素添加量的趋势如图4所示，抗压强度极差如图5所示。

由图4可见，充填体各龄期的抗压强度均随熟料添加量的增加而减小，且降幅随熟料添加量的增加而有所减小；随石膏添加量或芒硝添加量的增加呈现先减小后增加的趋势，且降幅明显低于增幅，随龄期增加，降幅基本不变而增幅明显降低。因此，可近似认为随着石膏添加量、芒硝添加量的增大，充填体的强度逐渐增加。

由图5可见，在3 d时，芒硝添加量的作用最大，高于熟料添加量、石膏添加量的作用效应，作用的重要性次序从大到小为芒硝添加量、熟料添加量和石膏添加量，芒硝起到了早强的作用。在56 d内，除3 d外熟料添加量的作用都是最大的，明显高于石膏添加量、芒硝添加量的作用效应，作用重要性次序为熟料添加量、芒硝添加量和石膏添加量。熟料作为最重要因素，熟料添加量的效应极差随时间的增大，先快速增大后缓慢减小，即作用效应随时间先快速增大后缓慢减小，与充填体抗压强度变化规律保持一致。

2.2  方差分析

限于篇幅，对充填体56 d的抗压强度，应用方差分析理论，分析得到各因素的离差平方和S_i、自由度f_i、均方离差和F_i值列于表4，相应于显著性水平为95%的F(2,2)的临界值分别为19.00。由表4得出，各因素对抗压强度影响的主次顺序为熟料添加量、芒硝添加量、石膏添加量，这与直观分析结果一致；熟料添加量的影响非常显著，石膏添加量的影响显著，芒硝添加量的影响不显著。

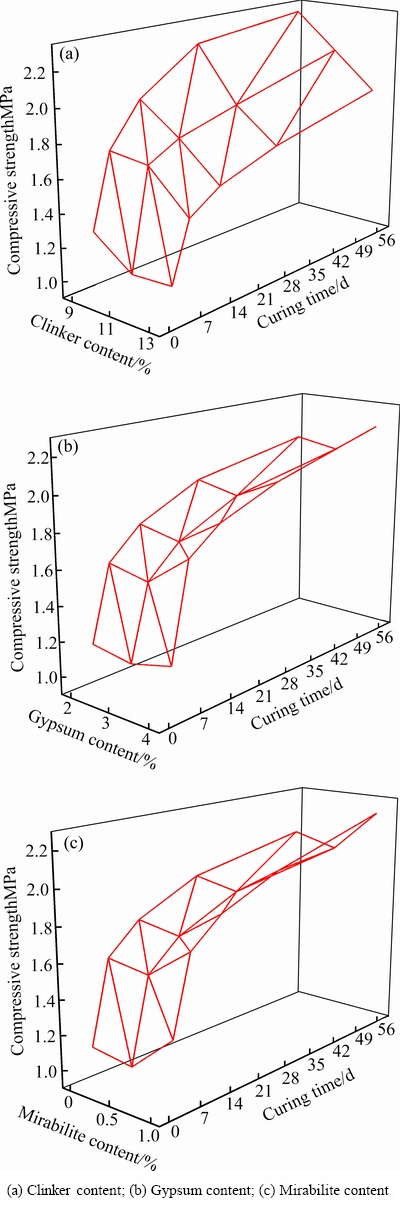
图4   胶结充填体效应趋势曲线

Fig. 4  Effect trend curves of cement filling body

图5  充填体抗压强度极差分析

Fig. 5  Range analysis of compressive strength of filling body

表4  充填体抗拉强度方差分析结果

Table 4  Variance analysis result of compressive strength for filling body

2.3  数据可视化

限于篇幅，将56 d正交试验结果以Origin数值模拟软件构建3D可视化模型，以熟料添加量、石膏添加量、芒硝添加量为空间坐标确定强度表征单元的位置，强度大小用颜色及右侧数字显示。图6所示为胶结充填体56 d强度可视化模型。由图6可以观测到存在交互作用时胶凝材料对充填体强度的影响规律：在熟料添加量为9%时，同时，增大石膏与芒硝添加量，充填体的强度呈增加趋势；在石膏添加量为2%时，同时，增大熟料与芒硝添加量，充填体的强度表现出先下降后缓慢上升的变化趋势；在芒硝添加量为0%时，同时增大石膏与熟料添加量，充填体的强度呈增大趋势。

3  优化配比与强度模型

3.1  胶凝材料配合比优化

图6  胶结充填体56 d强度3D可视化模型

Fig. 6  3D visualization model of cement filling body at 56 d strength

从试验结果和数据分析得到最优方案均是A1B3C3，为了确定真正的最优方案，利用正交试验设计中的效应计算分析方法^[20]，对分析的最优方案进行其指标值的预估计，将此指标预估计值和最优方案的指标值进行比较，确定真正的优化方案。

3.1.1  最优方案下的指标值的点估计

基于第2节分析，试验最优方案是A1B3C3，其中A是最重要的因素，取A1；C是次要因素，取C3；略去因素B，依据正交试验的效应计算式，可得到该方案的指标值点估计的表达式为

                           (1)

式中：为最优方案下指标值μ的点估计值；为A在1水平时对应指标值的平均值；为C在3水平时对应指标值的平均值；为试验指标值的平均值。

利用试验结果(见表3)进行点估计的计算，表5所示为点估计计算结果。不难发现，各龄期试验指标值的点估计值均小于试验最优指标，可初步判定胶凝材料配合比最优方案是A1B3C3。

3.1.2  最优方案下的指标值的区间估计

依据真正的μ值、点估计值和偏差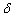的相互关系，以及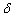满足误差F的临界值的关系式，可将区间估计和偏差表达为

                     (2)

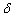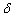式中：和为μ的估计区间的下限和上限；为偏差，且＞0。

表5  试验指标值最优点估计

Table 5  Best point estimation of test index value

                         (3)

式中：n_e为试验的有效重复数；f_E为误差的自由度； 在=0.05检验水平下的F分布临界值；M_SE为误差平方和的均方；计算中将因素B的离差平方和并入误差。

参照表4方差分析方法计算各龄期方差分析结果，结合表3和5的相关数据，分别计算n_e、f_E、S_E、M_SE、，并依次代入式(2)和式(3)，得到区间估计结果，如表6所示。

表6  试验指标值最优区间估计

Table 6  Best interval estimation of test index value

由表6可知，各龄期试验最优方案的指标值均在估计区间中，结合3.1.1点估计方法，可认为试验胶凝材料最优方案是A1B3C3，即熟料添加量为9%、石膏添加量为4%、芒硝添加量为1%。

3.2  充填体强度模型建立

在胶凝材料配合比优化分析中确定了胶凝材料的最优方案，但受胶凝材料添加方式和生产工艺的波动影响以及不同作业时间与方式的充填体强度目标不同，构建充填体强度模型可指导工程实践与预测。通过系统分析认为，本次实验决定充填体强度的主要因素有养护龄期、熟料添加量、石膏添加量与芒硝添加量。

为探究充填体抗压强度与养护龄期之间的定量关系，以拟合复相关系数R²作为评判标准，结合表3结果进行乘幂、对数和双曲线函数3种不同方式的拟合，拟合关系如表7所示。

表7  充填体强度与养护龄期拟合结果

Table 7  Fitting results between strength and times of filling body

由表7可知，乘幂、对数和双曲线3种拟合方式得到的平均复相关系数均很高，分别达到0.886，0.924和0.945。双曲线拟合结果优于前2种拟合结果，具有非常高的相关性，可较好地表征抗压强度与养护龄期之间的定量关系，其关系式为

                                (4)

式中：p₁和p₂为拟合参数；p₁为t趋向于无穷大时充填体的极限抗压强度，MPa；p₂为修正参数；t为养护龄期，d。

极限抗压强度p₁和修正参数p₂取决于胶凝材料配比，基于表7中p₁、p₂和表3中的材料配比，应用1stOpt软件拟合，采用标准简面体爬山法+通用全局优化法算法直至达到收敛判断标准，得到参数p₁和p₂的多元回归关系：

             (5)

                   (6)

式中：A为熟料添加量，%；B为石膏添加量，%；C为芒硝添加量，%。

回归模型中，p₁与A呈负相关，B、C呈正相关，与正交试验分析结果完全一致，可初步判定模型可靠。回归模型进一步采用F检验，模型p₁和p₂的自由度为3，剩余自由度为5，置信度为95%时，显著性检验临界值F_a为5.41。模型p₁的显著性检验值F=115.22，相关系数R²=0.943；模型p₂的显著性检验值F=46.63，相关系数R²=0.870。模型的显著性检验值F均大于临界值，相关系数R²均较大，模型与各因素的相关性好，拟合度高，置信度为95%时显著、可靠。

因素的显著性采用t检验，各因素的t值列于表8。置信度为95%时，临界值t_a为2.571，表8中除模型p₂的B因素外各因素的t值均大于临界值，说明各因素置信度为95%时基本显著。

表8  胶凝材料各组分因素的t值

Table 8  t values of each component factor for cementitious materials

为构建充填体强度模型，将式(5)、(6)代入(4)化简得到充填体强度数学模型：

  (7)

将胶凝材料配比最优方案A1B3C3代入模型公式(7)得出各龄期的抗压强度的模型计算值，结果如表9所示。由表9可知，养护14 d充填体的模型计算值(2.2 MPa)略大于试验最优指标(2.17 MPa)，养护3 d、7 d、28 d与56 d充填体的模型计算值略小于试验最优指标，模型计算值均落在最优估计区间中，因此，可初步判定模型具有一定的可靠信。

为进一步量化模型的可靠性，以(模型计算值-试验最优指标)/试验最优指标表征模型计算值误差率，以(点估计指标-试验最优指标)/试验最优指标表征点估计误差率，误差率计算结果列于表10。由表10可知，在3~56 d的5个龄期内，充填体模型计算值误差率分别低于点估计误差率-0.63%、4.28%、5.86%、2.97%和1.82%。同时，各养护龄期充填体模型计算值误差率绝对值均小于6%(以±6%为误差界限)，精度明显优于点估计误差率，能够满足工程实际需要，因此，充填体模型是可靠的。

表9  充填体强度数学模型计算结果

Table 9  Calculation results of mathematical model for filling body strength

表10  充填体强度数学模型计算结果误差率

Table 10  Error rate of calculation results for filling body strength mathematical model

4  结论

1) 基于直观分析、方差分析和可视化模型，充填体的抗压强度随熟料添加量的增大而减小，随石膏添加量和芒硝添加量的增大而增大，作用的重要性次序从大到小次序为熟料添加量、芒硝添加量和石膏添加量，熟料添加量的影响非常显著，是重要因素，石膏添加量的影响不显著，是次要因素。

2) 运用正交试验的效应估计分析方法，对比分析了试验最优方案和分析最优方案，验证得到试验最优方案与分析最优方案一致，即熟料添加量为9%，石膏添加量为4%，芒硝添加量为1%。

3) 采用胶凝材料配合比的熟料添加量、石膏添加量和芒硝添加量并考虑养护龄期的影响，建立了矿山充填体强度模型，并对模型进行检验验证，强度计算模型误差在6%以内，模型简单且具有良好的可靠性，可作为矿山工业充填的理论依据。

REFERENCES

[1] 李夕兵, 周 健, 王少锋, 等. 深部固体资源开采评述与探索[J]. 中国有色金属学报, 2017, 27(6): 1236-1262.

LI Xi-bing, ZHOU Jian, WANG Shao-feng, et al. Review and practice of deep mining for solid mineral resources[J]. The Chinese Journal of Nonferrous Metals, 2017, 27(6): 1236-1262

[2] 谢和平. “深部岩体力学与开采理论”研究构想与预期成果展望[J]. 四川大学学报(工程科学版), 2017, 49(2): 1-16.

XE He-ping. Research framework and anticipated results of deep rock mechanics and mining theory[J]. Journal of Sichuan University (Engineering Science Edition), 2017, 49(2): 1-16.

[3] 李夕兵, 曹芝维, 周 健, 等. 硬岩矿山开采方式变革与智能化绿色矿山构建—— 以开阳磷矿为例[J]. 中国有色金属学报, 2019, 29(10): 2364-2380.

LI Xi-bing, CAO Zhi-wei, ZHOU Jian, HUANG Lin-qi, et al. Innovation of mining models and construction of intelligent green mine in hard rock mine: In Kaiyang Phosphate Mine as an example[J]. The Chinese Journal of Nonferrous Metals, 2017, 2019, 29(10): 2364-2380.

[4] WANG Shao-feng, SUN Li-cheng, et al. Non-explosive mining and waste utilization for achieving green mining in underground hard rock mine in China[J]. Transactions of Nonferrous Metals Society of China, 2019, 29(9): 1914-1928.

[5] 李夕兵, 刘 冰, 姚金蕊, 等. 全磷废料绿色充填理论与实践[J]. 中国有色金属学报, 2018, 28(9): 1845-1865.

LI Xi-bing, LIU Bing, YAO Jin-rui, et al. Theory and practice of green mine backfill with whole phosphate waste[J]. The Chinese Journal of Nonferrous Metals, 2018, 28(9): 1845-1865.

[6] 杨 建, 王新民, 张钦礼, 等. 含硫高黏性三相流态充填浆体管道输送性能[J]. 中国有色金属学报, 2015, 25(4): 1049-1055.

YANG Jian, WANG Xin-min, ZHANG Qin-li, et al. Pipeline transportation properties of high viscosity sulfur-content filling slurry in three-phase flow[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(4): 1049-1055.

[7] 吴爱祥, 沈慧明, 姜立春, 等. 窄长型充填体的拱架效应及其对目标强度的影响[J]. 中国有色金属学报, 2016, 26(3): 648-654.

WU Ai-xiang, SHEN Hui-ming, JIANG Li-chun, et al. Arching effect of long-narrow cemented paste backfill body and its effect on target strength[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(3): 648-654.

[8] 张修香, 乔登攀, 孙宏生. 废石-尾砂高浓度料浆管道输送特性模拟[J]. 中国有色金属学报, 2019, 29(5): 1092-1101.

ZHANG Xiu-xiang, QIAO deng-pan, SUN Hong-sheng. Simulation on conveying characteristics in pipe about high-density slurry with waste rock-tailing[J]. The Chinese Journal of Nonferrous Metals, 2019, 29(5): 1092-1101.

[9] 姜立春, 苏 勇. 胶结充填体矿柱失稳的临界爆破振速理论模型及应用[J]. 中国有色金属学报, 2019, 29(11): 2663-2670.

JIANG Li-chun, SU Yong. Theoretical model and application of critical blasting vibration velocity for instability of cemented backfill pillar[J]. The Chinese Journal of Nonferrous Metals, 2019, 29(11): 2663-2670.

[10] MITCHELL R J, WONG B C. Behaviour of cemented tailings sands[J]. Canadian Geotechnical Journal, 2011, 19(3): 289-295.

[11] BELEM T, BENZAAZOUA M. Design and application of underground mine paste backfill technology[J]. Geotechnical and Geological Engineering, 2008, 26 (2): 147-174.

[12] MITCHELL ROBERT J. Model studies on cemented tailings used in mine backfill[J]. Canadian Geotechnical Journal, 2011, 19(1): 14-28.

[13] 付自国, 乔登攀, 郭忠林, 等. 超细尾砂胶结充填体强度计算模型及应用[J]. 岩土力学, 2018, 39(9): 3147-3156.

FU Zi-guo, QIAO Deng-pan, GUO Zhong-lin, et al. A model for calculating strength of ultra-fine tailings cemented hydraulic fill and its application[J]. Rock and Soil Mechanics, 2018, 39(9): 3147-3156.

[14] 聂亚林, 王晓军, 黄广黎, 等. 不同含水率纯尾砂胶结充填体强度及损伤模型分析[J]. 硅酸盐通报, 2018, 37(6): 2008-2013.

NIE Ya-lin, WANG Xiao-jun, HUANG Guang-li, et al. Strength and damage model analysis of pure tailings cemented filling body with different water content[J]. Bulletin of the Chinese Ceramic Society, 2018, 37(6): 2008-2013.

[15] 徐淼斐, 高永涛, 金爱兵, 等. 基于超声波波速及BP神经网络的胶结充填体强度预测[J]. 北京科技大学学报, 2016, 38(8): 1059-1068.

XU Miao-fei, GAO Yong-tao, JIN Ai-bing, et al. Prediction of cemented backfill strength by ultrasonic pulse velocity and BP neural network[J]. Journal of University of Science and Technology Beijing, 2016, 38(8): 1059-1068.

[16] 杨 啸, 杨志强, 高 谦, 等. 混合充填骨料胶结充填强度试验与优化配比决策研究[J]. 岩土力学, 2016, 37(S2): 635-641.

YANG Xiao, YANG Zhi-qiang, GAO Qian, et al. Cemented filling strength test and optimal proportion decision of mixed filling aggregate[J]. Rock and Soil Mechanics, 2016, 37(S2): 635-641.

[17] 曹 帅, 宋卫东, 薛改利, 等. 分层尾砂胶结充填体力学特性变化规律及破坏模式[J]. 中国矿业大学学报, 2016, 45(4): 717-722, 728.

CAO Shuai, SONG Wei-dong, XUE Gai-li, et al. Mechanical characteristics variation of stratified cemented tailing backfilling and its failure modes[J]. Journal of China University of Mining & Technology, 2016, 45(4): 717-722, 728.

[18] 兰文涛, 吴爱祥, 王贻明, 等. 基于正交试验的半水磷石膏充填配比优化[J]. 中国有色金属学报, 2019, 29(5): 1083-1091.

LAN Wen-tao, WU Ai-xiang, WANG Yi-ming, et al. Optimization of filling ratio of hemihydrate phosphogypsum based on orthogonal test[J]. The Chinese Journal of Nonferrous Metals, 2019, 29(5): 1083-1091.

[19] 吴疆宇, 冯梅梅, 郁邦永, 等. 连续级配废石胶结充填体强度及变形特性试验研究[J]. 岩土力学, 2017, 38(1): 101-108.

WU Jiang-yu, FENG Mei-mei, YU Bang-yong, et al. Experimental study of strength and deformation characteristics of cemented waste rock backfills with continuous gradation[J]. Rock and Soil Mechanics, 2017, 38(1): 101-108.

[20] 陈 魁. 试验设计与分析[M]. 北京: 清华大学出版社, 2006.

CHEN Kui. Test design and analysis[M]. Beijing: Tsinghua University Press, 2006.

Orthogonal experiment on ratio of whole tailings cementitious materials and strength model of filling body

WU Fan¹, GAO Qian¹, YANG Zhi-qiang^{1, 2}

(1. School of Civil and Resource Engineering, University of Science and Technology of Beijing, Beijing 100083, China;

2. Jinchuan Group Co., Ltd., Jinchang 737100, China)

Abstract: In order to determine the strength model of cemented filling body in ultra-deep iron ore, orthogonal test of the strength of filling body with full tailings cementing material ratio was carried out. The effects of cement clinker, desulfurization gypsum and industrial mirabilite on the strength performance of filling body were studied, and the strength model was established. The results show the strength of filling body decreases with the increase of cement clinker content, and then increases with the increase of desulfurization gypsum and mirabilite content. Full tailings cementing material optimization formula is clinker 9%, gypsum 4%, mirabilite 1%. Considering downhole operation time, the hyperbolic function relationship between the curing age and its strength was established, which reveals that strength increases first and then tends to be stable with increasing age. The concepts of the ultimate compressive strength p₁ and the revised parameter p₂ are proposed. By 1st Opt software, the relationship between the conceptual parameters and the cementitious materials addition is multivariate and non-linear. The strength model was established by synthesizing cementitious materials addition and curing age. The prediction error of model is less than 6%, which satisfies the engineering prediction accuracy and can be applied to develop full tailings cementitious materials and predict strength.

Key words: cementitious materials; orthogonal experiment; data visualization; ratio optimization; strength model

Foundation item: Project(2017YFC0602903) supported by the Key Research and Development Program of China

Received date: 2019-12-02; Accepted date: 2021-06-24

Corresponding author: GAO Qian; Tel: +86-18600173341; E-mail: gaoqian@ces.ustb.edu.cn

(编辑  李艳红)

基金项目：国家重点研发计划资助项目(2017YFC0602903)

收稿日期：2019-12-02；修订日期：2021-06-24

通信作者：高  谦，教授，博士；电话：18600173341；E-mail：gaoqian@ces.ustb.edu.cn