DOI: 10.11817/j.issn.1672-7207.2015.08.028
基于自适应因子设计的变形监测滤波算法
唐争气1, 2，宋迎春1，谢雪梅1，林东方1
(1. 中南大学 地球科学与信息物理学院, 湖南 长沙，410083；
2. 湖南城市学院 市政与测绘工程学院, 湖南 益阳，413000)
摘要：利用滤波正常时的残差向量必须服从正态分布的性质，提出1种滤波是否异常的假设检验方法，判断动态模型误差和观测粗差对变形监测滤波解的影响。研究结果表明：当滤波出现异常时，通过给定置信度的假设检验，确定自适应因子来调节误差较大的预报信息，从而较好地消除模型误差的影响；利用自适应抗差滤波解决变形监测数据处理中整体平衡观测信息和预报信息的贡献的问题，并通过实例验证算法的有效性和优良性。
关键词：自适应滤波；自适应因子；置信度；假设检验
中图分类号：P228.4 文献标志码：A 文章编号：1672-7207(2015)08-2957-05
Filter algorithm for slope monitoring with design of adaptive factor
TANG Zhengqi1, 2, SONG Yingchun1, XIE Xuemei1, LIN Dongfang1
(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;
2. School of Municipal and Surveying Engineering, Hunan City University, Yiyang 413000, China)
Abstract: Based on the statistical property that residual vectors should be normally distributed, a hypothesis test was proposed whether there is an exception in filter to control the influence of dynamic model errors and great error in observation on the status parameter estimation. The results show that when there is an exception in filter, an adaptive factor can be determined by means of a hypothesis test with a given confidence level, which can adjust forecast information with big error and resist the influence of modeling error. A robustly adaptive Kalman filter algorithm was given to solve the overall balance contribution between observations and forecasts in the deformation monitoring data processing. Then, the validity and excellent of the algorithm are verified through a example of deformation monitoring.
Key words: adaptive filtering; adaptive factor; confidence degree; hypothesis test
滑坡类型地质条件复杂，呈现多样性，决定了实时动态变形监测数据处理方法的多变性[1-7]。自适应抗差滤波具有控制观测异常和状态信息异常的能力[8]。在变形监测的数据处理中，为了能够平衡动力学模型信息与观测信息的权比以及控制动力学模型误差对状态参数解的影响，自适应抗差滤波必须设计1个合理且计算简便的自适应因子[1, 8]。合理地平衡观测信息和预报信息对状态估值的贡献，主要表现在2个方面：一种是平衡观测信息、预报信息各分量的贡献；另一种是整体平衡观测信息和预报信息的贡献。前一种平衡各分量的贡献主要由抗差等价权来实现，如抗差Kalman滤波；后一种平衡的实现方法有3种：1) 利用最新的观测残差和状态残差在线估计观测信息和预报信息的协方差矩阵[9-10]；2) 利用自适应因子从整体上平衡观测信息和预报信息对状态参数估值的贡献[11-12]；3) 将噪声协方差矩阵在线估计和自适应因子相结合[13-14]。目前已构造多种类型的自适应因子函数，如三段函数、两段函数和指数函数[15]。当状态向量各分量分别属于不同类型的参数时，有多因子滤 波[12]和参数自选权滤波[16]等方法。最优自适应因子[17]的合理性应该使得自适应滤波器的理论统计特性如状态向量估值的协方差阵、状态向量预测值的协方以及残差向量(新息向量)协方差与实际观测值的统计特性一致。由于无法知道实际噪声，状态向量估值在动态过程中无相应的参考值可以比较，状态向量的实际统计特性通常无法求得，导致确定自适应因子非常复杂。然而，在标准情况下，滤波应具有某些理论特性。当观测值可靠时，这种理论特性应与观测值信息相互匹配，否则将引起滤波异常。滤波的理论特性可以用残差向量的性质来刻画，当滤波模型和噪声特性都正确时，残差向量服从正态分布，由此可以建立一个统计假设检验来检验滤波是否有异常。在给定显著水平α下，通过假设检验若未发现滤波异常，则称滤波是自适应的。这种自适应针对一定的检验水平α而言，其中α为自适应水平，1-α为自适应的置信度。本文作者研究在给定显著水平α下，设计自适应因子以平衡动力学模型信息与观测信息的权比以及控制动力学模型误差对状态参数解的影响，在此基础上构造带有置信度的抗差自适应滤波算法。
1 自适应抗差滤波原理
在变形监测的滤波模型中，Kalman滤波常用离散化模型来描述，其线性化形式为[1]：
(1)
(2)
式中：Lk为m×1维观测向量；Ak为m×n维设计矩阵；Xk和Xk-1分别为第k和k-1历元的n×1维状态向量；Φk,k-1为n×n维状态转移矩阵；ek是协方差矩阵为
的n×1维观测噪声向量；Wk是协方差矩阵为
的n×1维状态噪声向量；ek与Wk不相关，且满足
，
(3)
(4)
由式(2)可得状态参数向量的预报值
及其协方差矩阵
为
(5)
(6)
式中：
为第k-1历元的位置和速度参数向量估值。则观测信息和状态预报信息的误差方程可写为
，
(7)
，
(8)
其中：Vk为观测残差向量；
为第k历元的位置和速度参数估值；Pk为观测权矩阵；
为预测残差向量；
为预报信息的权矩阵。
自适应抗差滤波解算原理为
(9)
式中：
为Lk的等价权矩阵；
为自适应因子矩阵。自适应抗差滤波解及其协方差矩阵可表示为
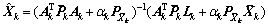(10)
(11)
2 自适应因子设计
当tk历元观测信息Lk可靠时，其相应的预测残差
(12)
反映了动力学模型的误差。从方程(12)和协方差矩阵的传播律可以得到预测残差的理论协方差阵：
(13)
在自适应滤波情形下，若动力学模型误差较大，则状态预测向量的权矩阵
应该减小，即应该变成
(0＜αk≤1)。相应地，其协方差矩阵
应该变成
，模型预测状态向量
的协方差阵被膨胀[2]。若历元 tk-1滤波正常，则自适应因子
=1，
(14)
若历元tk-1滤波异常，则自适应因子应小于1，这时，
(15)
于是，构造向量
(16)
则
服从自由度为m的
分布(其中，m为观测量的维数)，即
。有如下检验准则：当
时，滤波正常；当
时，滤波异常。其中，
为给定置信水平
从分布表中查得的门限值。
若通过上述检测未发现异常，则称滤波是自适应的。这种自适应是针对一定置信水平而言的。自适应滤波因子应在动力学模型误差较大时发挥作用。若在滤波过程中，由于动力学模型误差所作的自适应检测在容许的水平范围内，故不必进行自适应调节，此时对应的自适应因子为1。若在tk-1时刻发现滤波异常，则在下一个时刻tk运用自适应因子进行调节。令
，则
与时刻tk有关。当滤波正常时，应有
。若tk-1时刻滤波为异常，则
应该修改为
，以期修改后出现自适应性滤波。于是，对于这种滤波在自适应水平下，应有
，即
(17)
将式(17)作为自适应因子的一种约束。为了进行进一步改进，令
,
(18)
则Sk和Uk都是正定矩阵，因此，存在满秩矩阵Ck使
(19)
其中：
为
的根。由式(18)，有
令
，则有
(20)
满足式(20)的
不唯一。由于
为的单调递减函数，必存在使得
，
(21)
式(21)表示：若
，则
，此时，在tk时刻不进行自适应滤波。发生这种情况表示tk-1时刻经检测没有发现滤波异常。当
时，
，表示tk-1时刻检测到滤波异常，要对滤波进行自适应。其中自适应因子为
，利用可减少滤波异常最小限度，又能使滤波自适应，这样选择的自适应因子使得自适应滤波的置信度保持在
的水平上。
3 变形监测实例解算分析
以湖南某高速公路边坡监测为例[1]。该边坡已采用抗滑桩进行处治，在抗滑桩上布设观测点，观测三维位移。采用2台GPS接收机连续静态模式观测，采样率为15 s，基线每3 h计算1次结果，共观测6月。由于观测期间有1台GPS接收机时电池电量不足，导致某些时间段的观测数据出现一些异常，因此，位移的计算结果与实际不符。本例通过卡尔曼滤波和抗差自适应滤波对有异常的边坡观测数据进行处理，然后与正常接收机的监测结果进行比较，计算其相对误差。设计下面2种计算方案。
方案1：采用标准卡尔曼滤波计算。
方案2：采用自适应抗差滤波(式(10))进行计算，自适应因子按照式(21)计算，其中置信度α=0.10。
由这2种方案所得误差曲线分别如图1和图2所示。从图1和图2可以看出：
图1 方案1解算的误差曲线
Fig. 1 Error curves of Scheme 1
图2 方案2解算的误差曲线
Fig. 2 Error curves of Scheme 2
1) 由于观测机故障导致观测误差异常，利用方案1的标准卡尔曼滤波进行状态参数估计求得的形变位移的误差曲线(见图1)都出现了较大偏差，这说明异常观测对标准的卡尔曼滤波有较大影响。
2) 在方案2中，因为采用了自适应抗差滤波，其形变参数的滤波计算精度均有较大提高(见图2)，表明自适应因子起到了调控作用，较好地平衡了地球物理模型信息和观测信息对形变参数估计的贡献。然而，由于观测本身并不是可靠的，要完全修正观测比较困难。图2中，对于一些较小的抖动仍然无法修复。
3) 对比方案1和方案2的误差曲线可见：由于抗差自适应滤波算法可以有效地校正因观测异常导致的一些不合理的状态值，方案2的滤波结果抖动更小，符合变形观测实际情形。
4 结论
1) 为了分析模型误差的影响，建立1个假设检验，在给定的自适应水平下，检测滤波是否出现异常。
2) 若检测滤波有异常，则可以重新调整自适应因子，更好地遗忘误差较大的预报信息，从而有效地消除模型误差的影响。
3) 在变形监测数据处理中，提出一种基于假设检验的最优自适应因子确定方法以进行抗差自适应，平衡动力学模型信息与观测信息的权比，并控制动力学模型误差对状态参数解的影响。
参考文献：
[1] 左廷英，宋迎春. 带有未知物理信息的边坡监测滤波算法[J]. 武汉大学学报(信息科学版), 2012, 37(1): 86-90.
ZUO Tingying, SONG Yingchun. Filter algorithm for slope monitoring with unknown physical information[J]. Geomatics and Information Science of Wuhan University, 2012, 37(1): 86-90.
[2] 彭鹏, 单治钢, 董育烦, 等. 基于 Kalman 滤波融合算法的库区滑坡动态变形监测综合信息提取[J]. 岩石力学与工程学报, 2014, 33(8): 1520-1525.
PENG Peng, SHAN Zhigang, DONG Yufan, et al. Application of multi-sensor valuation in dynamic deformation for landslide monitoring based on Kalman filtration fusion theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(8): 1520-1525.
[3] 左廷英, 吴芸芸, 宋迎春. 滑坡监测的自适应约束抗差滤波算法研究[J]. 大地测量与地球动力学, 2011, 31(6): 94-99.
ZUO Tingying, WU Yunyun, SONG Yingchun. Adaptively robust constrained filtering algorithm[J]. Journal of Geodesy and Geodynamics, 2011, 31(6): 94-99.
[4] 章浙涛, 朱建军, 匡翠林, 等. 不同噪声下几种滤波方法的比较研究及改进[J]. 大地测量与地球动力学, 2014, 34(1): 127-130.
ZHANG Zhetao, ZHU Jianjun, KUANG Cuilin, et al. Comparative study and improvement on several de-nosing methods for different noises[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 127-130.
[5] 任超, 沙磊, 卢献健. 一种改进小波阀值算法的变形监测数据滤波方法[J]. 武汉大学学报(信息科学版), 2012, 37(7): 873-875.
REN Chao, SHA Lei, LU Xianjian. An adaptive wavelet thresholding de-noising for deformation analysis[J]. Geomatics and Information Science of Wuhan University, 2012, 37(7): 873-875.
[6] 章浙涛, 朱建军, 匡翠林, 等. 一种小波包混合滤波方法及其应用[J]. 武汉大学学报(信息科学版), 2014, 39(4): 471-475.
ZHANG Zhetao, ZHU Jianjun, KUNAG Cuilin, et al. A hybrid a filter method based on wavelet packet and its application[J]. Geomatics and Information Science of Wuhan University, 2014, 39(4): 471-475.
[7] 马攀, 孟令奎, 文鸿雁. 基于小波分析的Kalman滤波动态变形模型研究[J]. 武汉大学学报(信息科学版), 2004, 29(4): 349-353.
MA Pan, MENG Lingkui, WEN Hongyan. Kalman filtering model of dynamic deformation based on wavelet analysis[J]. Geomatics and Information Science of Wuhan University, 2004, 29(4): 349-353.
[8] YANG Yuanxi, HE Haibo, XU Guochang. Adaptively robust filtering for kinematic geodetic positioning[J]. Journal of Geodesy, 2001, 75(2/3): 109-116.
[9] 崔先强. 噪声协方差矩阵加权估计的Sage自适应滤波[J]. 测绘科学, 2002, 27(2): 26-30.
CUI Xianqiang. Sage adaptive filtering with the weighted prediction of the variance-covariance matrix[J]. Science of Surveying and Mapping, 2002, 27(2): 26-30.
[10] Mohamed A H, Schwarz K P. Adaptive Kalman filtering for INS/GPS[J]. Journal of Geodesy, 1999, 73(4): 193-203.
[11] 杨元喜, 高为广. 基于方差分量估计的自适应融合导航[J]. 测绘学报, 2004, 33(1): 22-26.
YANG Yuanxi, GAO Weiguang. Integrated navigation by using variance component estimates of multi sensor measurements and adaptive weights of dynamic model information[J]. Acta Geodretica et Cartographica Sinica, 2004, 33(1): 22-26.
[12] YANG Yuanxi, CUI Xianqiang, GAO Weiguang. Adaptive integrated navigation for multi-sensor adjustment outputs[J]. The Journal of Navigation, 2004, 57(2): 287-295.
[13] 徐天河, 杨元喜. 改进的Sage自适应滤波方法[J]. 测绘科学, 2000, 25(3): 22-24.
XU Tianhe, YANG Yuanxi. The improved method of Sage adaptive filtering[J]. Science of Surveying and Mapping, 2000, 25(3): 22-24.
[14] YANG Yuanxi, XU Tianhe. An adaptive Kalman filter based on Sage windowing weights and variance components[J]. The Journal of Navigation, 2003, 56(2): 231-240.
[15] YANG Yuanxi, GAO Weiguang. Comparison of adaptive factors in Kalman filters on navigation results[J]. The Journal of Navigation, 2005, 58(3): 471-478.
[16] REN Chao, OU Jikun, YUAN Yunbin. Application of adaptive filtering by selecting the parameter weight factor in precise kinematic GPS positioning[J]. Progress in Natural Science, 2005, 15(1): 41-46.
[17] YANG Yuanxi, GAO Weiguang. An optimal adaptive Kalman filter[J]. Journal of Geodesy, 2006, 80(4): 77-18.
(编辑 陈灿华)
收稿日期：2014-09-10；修回日期：2014-11-22
基金项目(Foundation item)：国家自然科学基金资助项目(41474008)；湖南省教育厅青年课题(12B022)(Project (41474008) supported by the National Natural Science Foundation of China; Project (12B022) supported by Youth Project of Education Department of Hunan Province)
通信作者：唐争气，博士研究生，副教授，从事盾构导向系统、变形监测数据处理与方法研究；E-mail:tzq_111@163.com
