Structure and resistance of concentration polar layer on cation exchange membrane-solution interface

SANG Shang-bin(桑商斌), HUANG Ke-long(黄可龙), LI Xiao-gang(李晓刚), WANG Xian(王 显)

School of Chemistry and Chemical Engineering, Central South University, Changsha 410083, China

Received 4 January 2006; accepted 17 July 2006

Abstract: Membrane/solution interface consists of a neutral concentration polar layer(CPL) and a charge layer(CL) under external electrical field, and the neutral CPL can be neglected under high frequency AC electrical field. The relationship of CL thickness e with electrolyte concentration C and fixed ion exchange sites density σ in membrane surface layer can be expressed as e=σ/C. According to this model, the thickness of the CL on Nafion1135 membrane/solution interface(e_c) was calculated under different membrane surface charge quantity Q and variable electrolyte concentration C. The membrane/solution interface CL thickness(e_m) is obviously related with the membrane properties, and decreases dramatically in a higher electrolyte concentration. e_m values are 76.3 nm and 110.3 nm respectively for Nafion1135 and PE01 ion exchange membrane in 0.05 mol/L H₂SO₄ solution, and e_m values for both membrane tend to 2 nm in 2 mol/L H₂SO₄ solution. For Nafion1135 membrane, the comparison of e_c and e_m gives the result that CL thickness e_m obtained by resistance measurement fits well with the calculated CPL thickness e_c while proton in CL transferred to membrane surface is 14.56×10^-10 mol, which corresponds to the fixed exchange group number in a surface layer with a thickness τ=2 nm for Nafion1135 membrane.

Key words: ion exchange membrane; AC electrical field; AC impedance; membrane/solution interface; structure; resistance

1 Introduction

Ion exchange membrane is widely used in many aspects such as eletrodialysis, chlorin alkali industry and fuel cell. Much attention has been kept on its importance in the fields of environment science, biology and material science. The concentration polar layer(CPL) on membrane-solution interface is one of the main factors which strongly influence the membrane properties[1,2]. Therefore the CPL structure and characteristic are important for membrane conductivity measurements. NOURI et al[3] studied the membrane conductivity by three different methods. The results by GUILLOU cell were lower than those by the other two methods especially in a solution with lower electrolyte concentration. However, the results tended to be equal when the electrolyte concentration increased. This study showed that the CPL thickness was related with not only membrane characteristic but also electrolyte concentration. Dielectric analysis by ZHAO[4] supported the conclusion mentioned above. In general, because of the ionization of membrane exchange sites (such as  ~SO₃—H ) in aqueous solution, the membrane surface is negatively charged, and electrical double layer(EDL) on membrane solution interface is formed. For example, Nafion resin is solid super acid, pK_a≈1[5], therefore the charge density of the membrane surface is related with electrolyte concentration. The charge density σ on the membrane surface is usually higher in a thin electrolyte than in a thick one because of the higher ionization of Nafion resin ion exchange groups. Therefore, the thickness of the formed electrical double layer is larger. The ion distribution in the electric double layer accords with Boltzmann distribution in a thin solution, and the theory results fit well with the experimental results[6]. However, in a thick solution, since the ions size and interaction cannot be ignored, the theory computation model would be modified[7].

The AC impedance technique is widely used in ion conductivity measurement of membrane because of the effect of CPL on the membrane/solution interface[8-12]. For membrane resistance measurement in electrolyte solution with GUILLOU cell by AC impedance method,the membrane resistance is calculated[6]:

                          (1)

where R_m is the membrane resistance, Ω; R_w is the resistance of solution with membrane, Ω; R_wt is the resistance without membrane, i.e. the solution resistance, Ω; d is the thickness of the membrane, mm; and a is the relation line slope of R_wt vs x, the distance of two electrode inner surfaces, Ω/mm.

The conductivity of the membrane is calculated by following equation[11,12]:

                                  (2)

where  d is the membrane thickness, cm; R_m is membrane resistance, Ω; and S is membrane area, cm².

Obviously, the effect of membrane/solution interface on the resistance measurement is not completely avoided especially in thin solution even under constant stirring. From the other hand, the membrane solution interface CPL under high frequency AC electrical field should be different from that without any outer disturbance as mentioned in Refs.[6,7] and is important for ion conductivity measurement by AC impedance technique.

In this study, the membrane/solution interface phenomena under high frequency AC electrical field are studied. The formation and structure of CPL are discussed in detail. The relations of CPL thickness with the electrolyte concentration and membrane property are investigated by two electrode AC impedance technique in variable H₂SO₄ electrolyte concentration.

2 Membrane/solution interface CPL model under AC electrical field

Figs.1(a) and (b) are schematic diagrams of ion transfer process, and Fig.1(c) is the schematic diagram of concentration distribution in CPL under external electrical field E.

As Fig.1(a) shows, in the right half cell, cations transfer across the membrane from right to left, since the transfer rate is much higher in membrane than in aqueous solution[13]. Therefore, at one time the membrane surface is negatively charged, and produces additional electrical field which enhances the outer electrical field E.  Protons in bulk solution transfer to the right side membrane surface to counteract the fixed ion exchange sites ~. While at the same moment, the anions  in bulk solution transfer to right, thus form the CPL on the right side membrane/solution interface with the right side CPL thickness represented by δ as shown in Fig.1(a).

In the left half cell, the left membrane surface is positively charged because the cation transfer rate in membrane is much higher than that in solution, part of cations accumulate on the left membrane surface, and at the same time, the anions  in left half cell solution transfer to right and counteract the positive charges on the left membrane surface, thus forming CPL on the left side of membrane/solution interface. Then CPL is formed on both sides of the membrane. The difference is that the concentration decreases on the right and rises on the left. The situation is opposite for Fig.1(b). E_r is the inner inverse electrical field, E_m is the inverse electrical field in membrane. Both of them reject the effect of external field E.

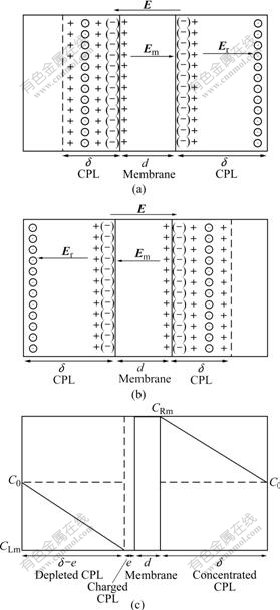
Fig.1 Schematic diagrams of membrane-solution interface concentration polar layer(CPL) model under electrical field ((-) is ~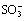;  ⊙ is ; + is H⁺; CPL is concentration polar layer; E is external electrical field; E_r is inverse electrical field in solution; E_m is inverse electrical field in membrane; δ is CPL thickness；e is charged layer thickness；d is membrane thickness; C₀ is bulk solution concentration; C_Lm is electrolyte concentration in left half cell depleted CPL; C_Rm is electrolyte concentration in right half cell concentrated CPL): (a) and (b) Membrane/solution interface CPL models under AC electrical field with opposite direction; (c) Ion distribution model in CPL under external electrical field

Fig.1(c) shows the concentration variation tendency in both membrane solution interfaces (corresponding to Fig.1(b)). Since the left membrane surface is negatively charged, a thin charged layer is formed on the vicinity of the membrane surface[13].

As Fig.1(b) shows, supposing that the membrane is homogeneous, and with identical property for both side surfaces, cation (proton) number transferred form left half cell solution to left membrane surface is equal to that transferred from left membrane surface to right membrane surface, and equal to that from right membrane surface to right half cell solution. Under the high frequency AC electrical field, the two CPLs exchange by each other. The effects are similar as protons transfer from one side across membrane to another side, and anions transfer across two CPLs. The proton transfer distance is 2δ+d, and the anion transfer distance is 2δ. The ion concentration in CPL in the left half cell is linearly distributed, C_Lm=C₀×[1-I/I_lim][14] as shown in Fig.1(c) (I_lim is the limited current of the membrane). C_Lm is usually larger than zero, and related with current density I, electrolyte concentration C₀ and membrane properties. Under high frequency electrical field, I?I_lim, therefore the concentration polarization is very weak, ΔC=C₀-C_Lm=C_Rm-C₀≈0, i.e, the effect of CPL can be ignored.  Nevertheless, the effect of charged layer on the membrane surface can not be ignored. From the analysis above, under high frequency AC electrical field, an additional electrical field on the membrane surface can be produced since the protons transfer faster in membrane, which accelerates the transfer of the protons in charged layer to membrane and the transfer of the anions 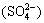 to bulk solution, thus the ion concentration in charged layer is very low. The thickness of the charged layer is represented as e. The ion number transferred from the solution of the charged layer to membrane surface layer is equal to that transferred from one side of membrane surface to the other side. So the following equation is obtained:

Sσ=CV                                      (3)

where  S is membrane area, m²; σ is membrane surface charge density, mol/m², approximately equal to the fixed ion exchange site density in a membrane surface layer thickness of τ; C is the concentration of electrolyte, mmol/L; V is the solution volume in the CPL, 10³L; V=Sδ, therefore,

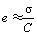                                      (4)

Nafion1135 membrane ion exchange capacity is C_s=1/1100 mol/g, thickness d=0.089 mm, density ρ＝2 g/cm³[12], and the unit area ion exchange capacity is about 1.62×10^-5 mol/cm². Supposing fixed ion exchange sites distribution in membrane are uniform, then exchange capacity at the unit thickness (τ) and unit area ion is 1.82×10^-10mol/(cm²?nm). The membrane area S=4.0 cm², thus the membrane ion exchange capacity of unit thickness(τ＝1 nm) is 7.28×10^-10 mol.

e can be calculated from Eqn.(4) with variable τ, and the results are listed in Table 1.

Eqn.(1) should be modified as

R_m+R_e=R_w-R_wt+(e+d)a                         (5)

where  R_e is the resistance of charged layer. According to our model, the ion conductivity in the charged layer can be calculated by formula conducted from infinite diluted electrolyte, therefore,

                                (6)

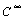where  K_e is the proton conductivity in CPL;  is the H₂SO₄ molar conductivity in infinite diluted solution, ＝859.6×10⁴ S?m²?mol^-1; is H₂SO₄ molar concentration in infinite diluted solution, 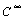≈10^-6 mol/L, thus the conductivity in charged layer is K_e= 859.6×10⁷ S?m^-1.

According to Eqn.(2):

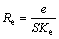                                  (7)

then the charged layer thickness e could be obtained by measuring R_e. The membrane area is 4×10^-4m2 in our experiments, therefore,

R_e=2.91×10⁷e                               (8)

e is usually very small compared with d and the ea term in Eqn.(5) can be ignored, thus we have Eqn.(10):

2.91×10⁷e=R_w-R_wt+da-R_m                    (10)

If the membrane resistance R_m can be obtained by other way, then the charged layer thickness e can be calculated.

H₂SO₄(AR, Hunan Normal University Chemisty Reagents Factor). Nafion1135 cation membrane(Tupont.Corp.) with thickness of 0.089 mm and ion exchange capacity of 0.97 meq/g (dry);  PE01 (Qianqiu Water Treatment Co. Ltd.), a kind of styrene(ST) -divinylbenzene(DVB) crosslinked and sulphonated product with thickness of 0.228 mm and ion exchange capacity of (2.0±0.2)meq/g(dry) were used.

Table 1 Relation of electrolyte concentration C₀ vs Nafion1135 membrane-solution interface charged layer thickness e

1) The membrane was washed three times with deionized water, then soaked into 0.5 mol/L H₂SO₄ with 0.5% H₂O₂ at 80 ℃ for 1 h, washed three times with deionized water and kept over night into the ready electrolyte for conductivity measurement.

2) The treated membrane with an area of 3 cm×3 cm was closely clipped between two half cell made by polyvinylchloride(PVC), and airproofed by an elastic silicon rubber gasket. The membrane effective area was 2 cm×2 cm. Two platinum electrodes with an area of 2 cm×2 cm were parallelly fixed on vernier caliper arms respectively as shown in Fig.2. The touched spot between electrode and vernier was insulated with rubber. Then the distance between two electrode inner surfaces could be adjusted by moving the mobile vernier caliper arm, and the precision was 0.01 mm.

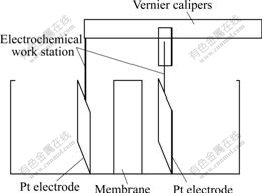
Fig.2 Schematic diagram of experimental set-up

3) Adjusting the vernier caliper position to assure the membrane and electrode in parallel position. The AC impedance tests were carried out by an Electrochemical Workstation(CHI660B, Shanghai Chenhua Instruments Corp.) in 0.05, 0.1, 0.5, 1.0 and 2.0 mol/L H₂SO₄ solution with membrane or without membrane. The frequency used was 100-10⁵ Hz and the voltage amplitude was 5 mV.

4.1 Relation of resistance with H₂SO₄ concentration and electrode distances

The resistances R_wt and R_w measured with Nafion1135 or PE01 membrane in variable H₂SO₄ concentration are shown in Fig.3.

From Fig.3, it can be seen that resistances R_wt(R_w) are linearly related to electrode inner surface distance x in certain concentration solution. R_wt(R_w)—x linear relation keeps well for all measured system. And we present all of these R_wt(R_w)—x line equation expressions by fitting experimental data with Origin7.0 software, as shown in Figs.3(a)-(e). The linear correlation coefficients are close to 0.99 for all of those lines.

The resistance R_m of Nafion1135 membrane can be calculated by the Nafion membrane conductivity (0.14 S?cm^-1) presented by Ref.[15] and Eqn.(2), and the calculated result is R_m=0.013 Ω. The conductivity of PE01 membrane is 0.043 S?cm^-1, and R_m=0.11Ω measured by Ref.[15]. R_e and charged layer thickness e_m in different concentration H₂SO₄ solution calculated by Eqn.(9) and Eqn.(10) are listed in Table 2.

The results from Table 2 show that e_m and R_e of PE01 membrane are larger than those of Nafion1135 membrane in all concentration ranges. The ion exchange capacity of PE01 membrane is  (2.0±0.2)meq/g(dry), larger than that of  Nafion1135 membrane, 0.97 meq/g(dry). This indicates that the charged layer thickness and resistance are related to the membrane surface layer density σ as Eqn.(4) suggests. e_m and R_e values decrease dramatically while the electrolyte concentration C₀  rises. The charged layer thickness e_m tends to a very close value of 2 nm in 2 mol/L H₂SO₄ solution for both of membranes. To Nafion1135 membrane, the measured results of charged layer thickness e_m from Table 2 is compared with calculated results e_c from Table 1, as shown in Fig.4.

From Fig.4, we can see that the measured e_m and the calculated e_c have the identical variation tendency. And the data fit well in all electrolyte concentration ranges while the membrane surface charge quantity is 14.56×10^-10 mol, which corresponds to the fixed exchange group number in a surface layer with a thickness τ=2 nm Nafion1135 membrane. The results support our theory model.

Table 2 Resistances R_e and thickness e_m of Nafion1135 and PE01 membrane/solution interface charged layer at different H₂SO₄ concentrations

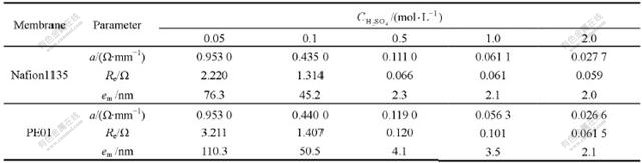
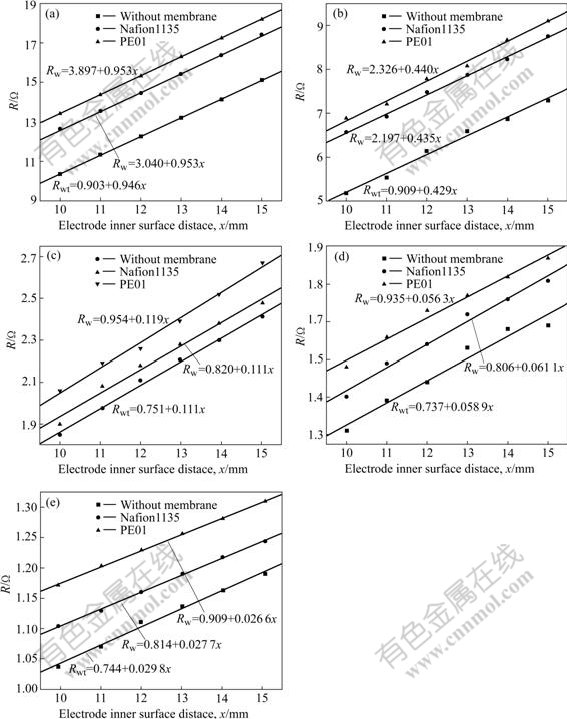
Fig.3 Resistances R_w(with membrane)and R_wt (without membrane) vs inner-electrode distance x for different membranes in variable H₂SO₄ concentration solution: (a) 0.05 mol/L H₂SO₄; (b) 0.1 mol/L H₂SO₄; (c) 0.5 mol/L H₂SO₄; (d) 1.0 mol/L H₂SO₄; (e) 2.0 mol/L H₂SO₄

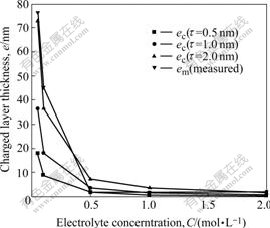
Fig.4 Comparison of Nafion 1135 membrane charged layer thickness e_m and e_c

5 Conclusions

1) Concentration polar layer(CPL) on membrane/ solution interface consists of a neutral one and a charge layer(CL) under external electrical field.  The neutral one can be ignored under high frequency AC electrical field.

2) The CPL thickness e is in proportion to membrane surface layer charge density σ, and is inversely related with electrolyte concentration C₀, e= σ/C₀.

3) The resistance of membrane/solution interface measured by AC impedance technique supports our model.

4) To Nafion1135 membrane, the amount of protons in charged layer transfer to membrane surface is 14.56×10^-10 mol, which corresponds to the fixed ion exchange number in the thickness τ＝2 nm of a surface layer.

[1] CHOI J H, PARK J S, MOON S H. Direct measurement of concentration distribution within the boundary layer of an ion-exchange membrane [J]. Journal of Colloid and Interface Science, 2002, 251: 311-317.

[2] PENG C, MENG H, SONG S, LU S, LOPEZ-VALDIVIESO A. Secondary potential in electrodialysis membranes and the effect on permselectivity [J]. Journal of Colloid and Interface Science, 2004, 273: 256-261.

[3] NOURI S, DAMMAK L, BULVESTRE G, AUCLAIR B. Comparison of three methods for the determination of the electrical conductivity of ion-exchange polymers [J]. European Polymer Journal, 2002, 38: 1907-1913.

[4] ZHAO K S. Dielectric relaxation of heterogeneous systems with planar structure—influence of the number and the electric conductivity of constituent phases on the relaxation pattern [J]. Chinese Journal of Electrochemistry, 1995, 1(3): 320-326.

[5] REN X, WILSON M S, GOTTESFELD S. High-temperature proton conducting membranes based on perfluorinated ionomer membrane-ionic liquid composites [J]. J Electrochem Soc, 2000, 147: 34-42.

[6] RICHARD BOWEN W, DONEVA TEODORA A, AUSTIN G, STOTON J. The use of atomic force microscopy to quantify membrane surface electrical properties [J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2002, 201: 73-83.

[7] BOHINC K, KRALJ-IGLIC V, IGLIC A. Thickness of electrical double layer: effect of ion size [J]. Electrochimica Acta, 2001, 46: 3033-3040.

[8] GAVACH. C, PAMBOUTZOGLOU G, NEDYALKOV M, POURCELLY G. AC impedance investigation of the kinetics of ion transportation in Nafion perfluorosulfonic membranes [J]. J Membra Sci, 1989, 45: 37-42.

[9] DESLOUES C, MUSIANI M M, TRIBOLLET B, VOROTYNTSEVET M A. Comparison of AC impedance of conducting polymer films studied as electrode supported and free standing membranes [J]. J Electrochem Soc, 1995, 142(6): 1902-1908.

[10] SONE Y, EKDUNGE P, SIMONSSON D. Proton conductivity of Nafion117 as measured by four electrode AC impedance method [J]. J Electrochem Soc, 1996, 143(4): 1254-1259.

[11] NWAL AMANG D, ALEXANDROVA S, SCHAETZEL P. The determination of diffusion coefficients of counter ion in an ion exchange membrane using electrical conductivity measurement [J]. Electrochim Acta, 2003, 48: 2563-2569.

[12] POURCELLY G, SISTAT P, CHAPOTOT A, GAVACH C, NIKONENKO V. Self diffusion and conductivity in Nafion membrane in contact with NaCl+CaCl₂ solution [J]. J Membra Sci, 1996, 110: 69-78.

[13] PENG C, MENG H, SONG S, LU S, LOPEZ-VALDIVIESO A. Secondary potential in electrodialysis membranes and the effect on permselectivity [J]. J Colloid Interf Sci, 2004, 273: 256-261.

[14] CHOI J H, PARK J S, MOON S H. Direct measurement of concentration distribution within the boundary layer of an ion-exchange membrane [J]. J Colloid Interf Sci, 2002, 251: 311-317.

[15] SILVA R F, DE FRANCESCO M, POZIO A. Tangential and normal conductivities of Nafion^? membranes used in polymer electrolyte fuel cells [J]. J Power Sources, 2004, 134: 18-26.

(Edited by YANG Bing)

Foundation item: Project(02-09-01) supported by Panzhihua Iron and Steel Corporation, China

Corresponding author: SANG Shang-bin; Tel: +86-731-8836618; Fax: +86-731-8879616; E-mail: shbsang@yahoo.com.cn