磁悬浮球的鲁棒控制器设计
李群明,朱 伶,徐 震
(中南大学 机电工程学院,湖南 长沙,410083)
摘 要:为了掌握磁浮支承的设计和控制原理,设计一种新型的磁悬浮球实验装置,建立其动力学模型。应用H∞混合灵敏度控制理论,通过合理选取加权函数,设计该实验装置的H∞鲁棒控制器,并采用数字控制方法,对其离散化后用DSP系统实现了其稳定控制。仿真和实验结果表明:与传统的PID控制方法相比,基于H∞控制理论设计的磁悬浮球控制器具有更好的动态性能,如系统起浮时的超调量从0.8 mm降低到0.4 mm,稳态偏差从原来的0.35 mm降低到0.10 mm,且具有更快的响应速度和更强的鲁棒性。
关键词:磁悬浮球系统;鲁棒控制;H∞混合灵敏度;数字信号处理器
中图分类号:TP273.24 文献标识码:A 文章编号:1672-7207(2007)05-0922-06
Robust controller design of maglev ball system
LI Qun-ming, ZHU Ling, XU Zhen
(School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)
Abstract: In order to understand the principle of magnetic levitated bearings and verify the control methods, a device of levitating a small steel ball was designed and its dynamic model was constructed. The H∞ mixed sensitivity control method was used. The selection methods for the H∞ weighting functions were discussed and a H∞ controller was designed to improve accuracy and robustness. Its real-time control was implemented by DSP systems. The simulation and experimental results show that the H∞ controller is more effective than previous PID controller, for example, the peak overshoot decreases from 0.8 mm to 0.4 mm, and the steady-state error decreases from 0.35 mm to 0.10 mm. The response speed is quicker, and the robustness is also improved.
Key words: maglev ball system; robust control; H∞ mixed sensitivity; digital signal processor (DSP)
磁悬浮技术是利用电磁力将动子悬浮起来,使动子和定子之间没有任何机械接触的一种新型高性能支承技术,具有无摩擦、无磨损、无需润滑、寿命长、支承力可控、刚度阻尼可调并可在线监测等一系列优点,已经在很多领域得到应用,如磁浮列车、磁浮轴承、磁浮隔振器、微电子封装、光刻等[1-4]。磁悬浮系统中,控制器是核心[5],不仅关系到磁浮支承工作的稳定性,而且决定磁浮支承的承载特性和刚度阻尼特性,影响系统的动态性能。目前广泛采用PID控制[6]和最优控制[7],虽然这些控制易于实现,但存在参数整定困难,控制律适应性差等缺点。变结构[8]及自适应控制[9]可有效提高系统鲁棒性,但稳态性能较差。H∞鲁棒控制是新发展的频域内最优控制理论[10-12],其应用日益广泛,如J. H. Yi等[13]及Y. Uchiyama等[14]分别应用H∞控制和?综合控制均取得了较好的效果。在此,本文作者针对早期设计的磁悬浮球实验装置,采用H∞鲁棒控制理论对控制器进行了优化设计,其仿真及实验结果达到了预期要求。
1 磁悬浮球系统的动力学模型
1.1 磁悬浮球实验系统的结构
磁悬浮球系统的结构如图1所示,主要由铁芯、线圈、光源、传感器、控制器、功率放大器、被悬浮钢球等元件组成。通过控制流经励磁线圈的电流来控制电磁力,从而平衡钢球重力,使钢球在给定平衡位置处于稳定悬浮状态。
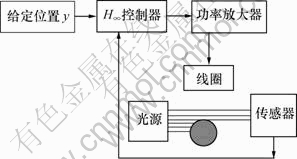
图1 磁悬浮球实验系统结构
Fig.1 Structure of magnetic suspended ball system
1.2 磁悬浮球的动力学模型
图2所示为钢球受力分析图。图中:i为励磁电流; 为扰动电流;I 为平衡位置处电磁力与重力相等时的电流;Y为平衡位置处钢球到电磁铁下端面的距离;y为钢球到电磁铁下端面的位移;
为扰动电流;I 为平衡位置处电磁力与重力相等时的电流;Y为平衡位置处钢球到电磁铁下端面的距离;y为钢球到电磁铁下端面的位移; 为钢球偏离平衡位置的位移,坐标方向规定向下为正。
为钢球偏离平衡位置的位移,坐标方向规定向下为正。
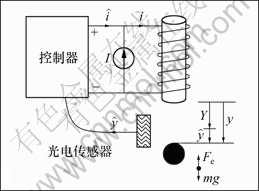
图2 磁浮球受力分析
Fig.2 Force analysis for ball
当钢球相对于平衡位置向下运动时,光电传感器检测到小球位置的变化信号,并反馈给控制器以增大励磁电流,将钢球拉回平衡位置处;反之,当钢球相对于平衡位置向上运动时,控制器则减小控制电流,由重力使钢球回复到平衡位置处,从而实现动态悬浮。
根据电磁场能量方程及虚功原理可得电磁力的计算公式为:

本系统中,L1=123.6 mH,L0=8.3 mH,a=4.2 mm。
将式(2)代入式(1)并取偏导得电磁力表达式为:
 。 (3)
。 (3)
小球的运动方程为:

假设钢球在平衡位置时y=Y,i=I,将式(3)代入式(4),则有如下关系成立:
 。 (5)
。 (5)
由式(5)可以看出,对于给定的电流I,钢球的悬浮位置Y也为一确定值。
令
 ;
; 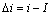 。 (6)
。 (6)
将电磁力方程在平衡位置处泰勒展开,略去高阶项得到线性化方程如下:
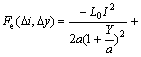
 。 (7)
。 (7)
将式(5),(6)和(7)代入式(4)可以得出小球线性化处理后的运动微分方程:
 。 (8)
。 (8)
对式(7)进行拉氏变换,从而得到系统的开环传递函数:
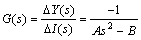 。 (9)
。 (9)
式中:
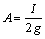 ,
,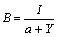 。
。
由式(9)可以得出磁悬浮小球系统的开环极点为:
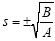
可以看出,开环控制时系统有1个极点位于复平面的右半平面,即开环系统是不稳定的,必须采用反馈控制。
本文磁悬浮系统中,钢球质量m=60 g,平衡位置Y=13 mm,平衡时静态电流I=452 mA。将相关参数分别代入式(8)和(9)可得系统从线圈电流 到钢球位置
到钢球位置 的开环传递函数为
的开环传递函数为
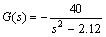 。 (10)
。 (10)
2 磁浮球的鲁棒控制器设计
2.1 鲁棒控制设计理论
磁悬浮系统的控制目标是通过调整加在电磁铁线圈中的电流变化量i,使钢球无接触地稳定悬浮在空中。基于式(10)的传递函数模型,应用鲁棒控制理论,可将控制问题设定为混合灵敏度控制问题,通过合理选取加权函数使系统的灵敏度函数和补灵敏度函数按希望的规律变化以满足系统所需的各项性能指标要求。H∞混合灵敏度控制的标准结构如图3所示[10-14]。图中:G为开环传递函数;K为要求的鲁棒控制器;r,e,u,d,n,z和y分别为参考输入、跟踪误差、控制量输入、干扰输入、量测噪声、评价系统输出和系统输出, ;W1(s),W2(s)和W3(s)分别为系统的性能权,控制器输出权和鲁棒权。从参考输入r到e,u和y的闭环传递函数分别为:
;W1(s),W2(s)和W3(s)分别为系统的性能权,控制器输出权和鲁棒权。从参考输入r到e,u和y的闭环传递函数分别为:
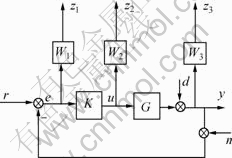
图3 H∞混合灵敏度问题的标准框架
Fig.3 Standard model of 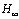 mixed sensitivity problems
mixed sensitivity problems

对于磁悬浮球系统,将给定的钢球的平衡位置作为外界输入,r和u作为控制器输入,跟踪误差和球的偏移位置作为广义受控对象的输出,磁浮球的H∞混合灵敏度控制器设计问题就是寻找正则的有理函数控制器K(s),使系统闭环稳定,且闭环系统增广对象闭环传递函数 满足
满足
 (γ≥γ0)。 (12)
(γ≥γ0)。 (12)
这就使磁悬浮球系统的控制问题变成了混合灵敏度控制设计问题。
2.2 加权函数的选择
鲁棒控制器的设计过程主要是对S,T和R的加权W1(s),W2(s)和W3(s)的选择过程。本系统中,加权的选择遵循如下原则[10-13]:
W1(s)的选择方法:S是系统参考输入到跟踪误差的传递函数,也是系统干扰输入到系统输出的传递函数。对于磁悬浮系统,干扰通常发生在低频范围,为了抑制干扰,希望S的增益尽量小,所以,低频段的加权值应尽量大,所选W1(s)应为具有低通性质的真实有理函数,即W1反映了干扰的频谱特性。若低频干扰的频宽为ω1,则取W1(s)的转折角频率ω≥ω1,若不能满足,则可将W1取为二阶函数,并且W1(s)满足:
 ≤
≤ 。 (13)
。 (13)
式中: 表示最大奇异值。
表示最大奇异值。
W3(s)的选择方法:W3(s)表示乘性摄动的范数界,频率特性应具有高通性质,其上升斜率可取大些,以保证闭环系统对高频干扰的抑制。对于给定的频率,如果要求S的增益很小,那么T将近似为I,由性能指标可看出W3(s)必须很小,从而降低了系统的鲁棒稳定性,降低T的增益,这样势必引起S的增益变大。
解决这个矛盾的办法:在低频段以减小灵敏度函数S的增益为主,而在高频段以减小互补灵敏度函数S的增益为主,将W3(s)取为具有高通性质的有理函数,并且使W1(s)与W3(s)的频带不重叠,即二者的剪切频率之间有一定距离。在实际工程中,干扰的频带多为低频信号,而未建模动态往往是高频信号,因此,这种折衷设计思想是合理的。
W2(s)是对R的加权评价函数,表示加性摄动的范数界。引入W2(s)有以下几方面作用:
a. 引入W2(s),可以限制控制量u的大小,防止系统在实际工作过程中产生严重的饱和现象以及控制量过大而导致执行器被损害。从这个角度出发,W2(s)的静态增益应该适当大。
b. W2(s)的选择对系统的带宽也有很大的影响。实际上,当W2(s)的幅值由小变大时,解算出来的控制系统剪切频率则由大变小。为了保证系统有足够的带宽,W2(s)的静态增益应该适当小。
为不增加控制器的阶次,通常可将W2(s)取为一常实数,此时表示加性摄动为一常数界。在一定范围内,W2取值越大,则 越小。在混合灵敏度设计中,W1和W3确定后,W2可以作为一个加权常数进行调整,以获得中低频内有较大鲁棒稳定性的参数摄动范围。
越小。在混合灵敏度设计中,W1和W3确定后,W2可以作为一个加权常数进行调整,以获得中低频内有较大鲁棒稳定性的参数摄动范围。
3 实验分析
依照前面介绍的设计原则,在本磁浮球系统中,首先把灵敏度函数 的加权函数W1(s)选择为一阶的有理函数:
的加权函数W1(s)选择为一阶的有理函数:
 ,
,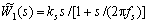 。 (14)
。 (14)
依照前面介绍的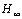 控制器设计方法和加权阵的选择原则,经过反复仿真计算和实验比较,最终确定选择γs=1, ks=500, fs=6.605×10-5。
控制器设计方法和加权阵的选择原则,经过反复仿真计算和实验比较,最终确定选择γs=1, ks=500, fs=6.605×10-5。
补灵敏度函数T(s)的加权函数为W3(s),表示乘性摄动的范数界,将其选择为一个二阶的多项式
 。 (15)
。 (15)
经反复实验比较后确定选取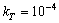 ,
, ,
, 。
。
在混合灵敏度设计中,W2(s)可以作为一个加权常数进行调整,以获得中低频内有较大鲁棒稳定性的参数摄动范围。本设计中,取W2(s)=0。
在确定加权函数后,应用Matlab鲁棒控制工具箱求解可得到系统控制器为:

闭环系统增广对象闭环传递函数的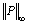 曲线如图4所示。可见,当
曲线如图4所示。可见,当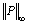 ≤1时,闭环系统稳定。系统仿真结果满足设计要求。
≤1时,闭环系统稳定。系统仿真结果满足设计要求。
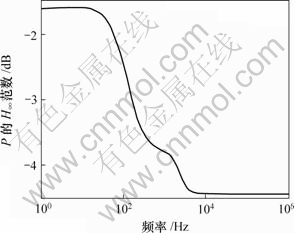
图4 增广对象传递函数P的H∞范数曲线
Fig.4 H∞ norm curve for augmented system P
其离散化方程为:
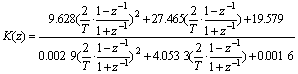 。 (17)
。 (17)
将控制器的输入输出关系用差分方程表示,得其数字控制方程为:
 。(18)
。(18)
式中:
k0=0.001 6 T2+8.106 6 T+0.001 6,
k1=19.579 T2-54.93 T+38.512,
k2=39.158 T2-77.024,
k3=19.579 T2+54.93 T+38.512,
k4=0.001 6 T2-8.106 6 T+0.001 6,
k5=0.003 2 T2-0.002 32。
其中:E(k)是k时刻控制器的偏差输入;u(k)为k时刻控制器的输出。
实验中采样周期T设定为1 ms,根据式(18)利用DSP采用1 ms定时中断方式设计线圈电流的数字控制程序,经D/A转换并进行功率放大后输入电磁线圈,使钢球受到的重力与电磁吸力保持动态平衡。
图5所示为应用H∞控制器得到的实验结果,控制算法离散化后用美国TI公司的TMS320LF2407 DSP系统设计实现。由图可见,系统工作情况表明该控制系统具有较高的鲁棒性能。

(a) 单个小球稳定悬浮时的工作情况;(b) 将钢球改为六角螺母以使悬浮体质量发生变化时的稳定工作情况
图5 H∞控制时磁浮球系统的实验实况
Fig.5 Experimental results of maglev system with H∞ controller
图6所示为应用H∞控制器得到的系统稳定工作时位置传感器的输出波形,图7所示为早期采用PID控制得到的稳态输出。可以看出,应用H∞控制时系统输出纹波较小,最大稳态位置误差为0.10 mm,比采用PID控制时的误差小0.25 mm。
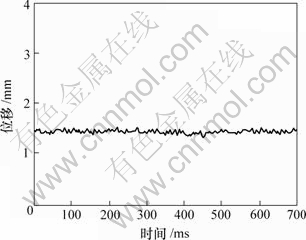
图6 H∞控制时的稳态位移输出波形
Fig.6 Stable output of ball displacement with H∞ controller
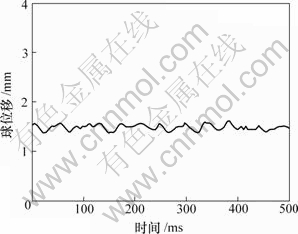
图7 PID控制时悬浮球的稳态位移输出波形
Fig.7 Stable output of levitated ball with PID controller
图8所示为悬浮体质量发生变化时系统的阶跃响应。可见,浮球质量在一定范围内变化时,系统可以很快到达平衡状态,表明了H∞控制器对模型摄动具有很强的抑制能力。另一方面,H∞控制器也可以对外界低频干扰起到很好的抑制作用,当突加干扰时,系统可以在很短的时间内恢复稳定。图9所示为突加外界干扰时的位置传感器输出。可见,系统在外界干扰存在的情况下同样具有快速的稳定性。
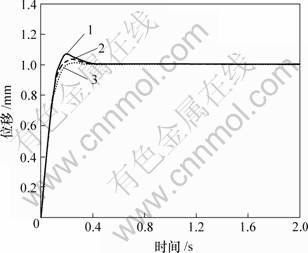
m/g: 1—40; 2—50; 3—60
图8 质量发生变化时钢球的阶跃响应
Fig.8 Step responses with changed ball mass
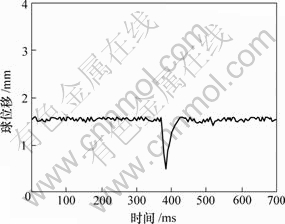
图9 外加干扰时钢球运动的位移波形
Fig.9 Disturbed output response of levitated ball
4 结 论
a. 针对自行设计的一种磁悬浮小球实验装置,建立了该系统的动力学模型,设计了其H∞鲁棒控制器,并进行了仿真和实验研究。
b. 与原来采用的PID控制方法相比,基于鲁棒控制理论设计的磁悬浮球控制器具有更快的响应速度、更高的控制精度和更强的鲁棒稳定性,如最大稳态位置误差小于0.10 mm,比采用PID控制时的误差小 0.25 mm;钢球质量从40~60 g范围内动态变化时,均能在0.3 s内迅速回复到平衡状态。
c. 系统在受到外界突加扰动时能够迅速回复到平衡位置,稳定悬浮时的随机抖动现象显著减少。
参考文献:
[1] Kim W J, Trumper D L. High-precision magnetic levitation stage for photolithography[J]. Precision Engineering, 1998, 22(2): 66-77.
[2] 许良琼, 陆新江, 李群明. 模糊PID控制在磁悬浮平台中的应用[J]. 中南大学学报: 自然科学版, 2005, 36(4): 631-636.
XU Liang-qiong, LU Xin-jiang, LI Qun-ming. Application of fuzzy-PID control to electromagnetic suspension platform[J]. Journal of Central South University: Science and Technology, 2005, 36(4): 631-636.
[3] Lyons J P, Preston M A, Gurumorthy R, et al. Design and control of a fault-tolerant active magnetic bearing system for aircraft engines[C]//Proceedings of the 4th International Symposium on Magnetic Bearings. Zurich, 1994: 449-454.
[4] Lepetic M, Skrjanc I, Chiacchiarini H G, et al. Predictive functional control based on fuzzy model: magnetic suspension system case study[J]. Engineering Applications of Artificial Intelligence, 2003, 16: 425-430.
[5] Lin C S, Lay Y L, Chen P W, et al, The laser displacement measurement with feedback control in a magnetic levitation and suspension system[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 90: 25-34.
[6] Stephen C, Paschall II. Design, fabrication, and control of a single actuator magnetic levitation system[D]. Texas: Department of Mechanical Engineering, Texas A&M University, 2002.
[7] 朱熀秋, 徐龙祥. 径向四自由度主动磁悬浮轴承控制器研究与探讨[J]. 应用科学学报, 2002, 20(1): 55-60.
ZHU Huang-qiu, XU Long-xiang. A study and discussion on a controller for radial four-degree freedom active magnetic bearing[J]. Journal of Applied Sciences, 2002, 20(1): 55-60.
[8] Hassan I M, Mohamed A M, Saleh A I. Variable structure control of a magnetic suspension system[C]//Proceedings of the 2001 IEEE International Conference on Control Applications. Mexico, 2001: 333-336.
[9] Gentili L, Marconi L. Robust nonlinear disturbance suppression of a magnetic levitation system[J]. Automatica, 2003, 39: 735-742.
[10] 吴旭东, 解学书. H∞鲁棒控制中的加权阵选择[J]. 清华大学学报: 自然科学版, 1997, 37(1): 27-30.
WU Xu-dong; XIE Xue-shu. Weighting function matrix selection in H∞ robust control[J]. Journal of Tsinghua University: Natural Science, 1997, 37(1): 27-30.
[11] 吴 敏, 桂卫华. 现代鲁棒控制[M]. 长沙: 中南工业大学出版社, 1998.
WU Ming, GUI Wei-hua. Modern robust control[M]. Changsha: Press of Central South University of Technology, 1998.
[12] 桂卫华, 刘碧玉. 一类不确定时滞关联非线性系统分散鲁棒H∞控制[J]. 中南大学学报: 自然科学版, 2005, 36(5): 132-137.
GUI Wei-hua, LIU Bi-yu. Decentralized robust H∞ control for a class of uncertain interconnected nonlinear systems with time delays[J]. Journal of Central South University: Natural Science, 2005, 36(5): 132-137.
[13] Yi J H, Park K H, Kim S H, et al. Robust force control for a magnetically levitated manipulator using flux density measurement[J]. Control Engineering Practice, 1996, 4(7): 957-965.
[14] Uchiyama Y, Mukai M, Fujita M. Robust acceleration control of electrodynamic shaker using μ–synthesis[C]//Proceedings of the 44th IEEE Conference on Decision and Control. Seville, 2005: 6170-6175.
收稿日期:2007-01-11;修回日期:2007-02-25
作者简介:李群明(1969-),男,湖南宁远人,副教授,博士,从事机电控制技术研究
通信作者:李群明,男,博士;电话:0731-8830291;E-mail: liqm@mail.csu.edu.cn