文章编号：1004-0609(2009)02-0208-09

半固态挤压铝/镁合金双金属复合管的有限元模拟

杜艳梅¹，王开坤^{1, 2}，张  鹏¹，马春梅¹，徐  锋¹

(1. 北京科技大学 材料科学与工程学院，北京 100083；

2. 清华大学 机械工程系，北京 100084)

摘  要：为了研究双金属复合管挤压参数及其结合面的情况与挤压参数的关系，基于热力耦合的有限元原理，采用ABAQUS有限元软件，通过建立合理的有限元分析模型，对Al/Mg双层复合管在半固态多坯料挤压工艺下进行数值模拟研究，得到变形体在不同变形温度下的温度场和应力、应变分布，确定界面比为3:7的挤压速度和初始温度，优化挤压模具，同时，结合速度分析结合界面的结合情况。

关键词：半固态成形；多坯料挤压；双层复合管；有限元模拟；热力耦合

中图分类号：TG 249       文献标识码： A

FEM simulation on extrusion of double-layer tube of

aluminum and magnesium alloys

2DU Yan-mei¹, WANG Kai-kun^{1, 2}, ZHANG Peng¹, MA Chun-mei¹, XU Feng¹

 (1. School of Materials Science and Engineering, University of Science and Technology Beijing,

Beijing 100083, China;

2. Department of Mechanical Engineering, Tsinghua University, Beijing 100084, China)

Abstract: In order to study the extrusion parameters of the double-layer tube and the interaction between the interface and the extrusion parameters. The process of bonding for the double-layer tube of Al/Mg by thixo-co-extrusion was analyzed by ABAQUS FEM microsoft based on the thermal-mechanical coupling finite element method (FEM) theory and finite model. The temperature field and the distribution of the stress and the equivalent strain in the sample on the process of binding by thixo-co-extrusion were also achieved. The velocity laws of component metal on the deforming process of the extrusion were analyzed with three kinds of bonding proportions. The extrusion speed and the initial temperature at the bonding proportion of 3:7 are available. And the extrusion die is also optimized. At the same time the varying of the interface between inner and outer metal along with the velocity is obtained.

Key words: semi-solid forming; thixo-co-extrusion; double-layer tube; FEM simulation; thermal-mechanical coupling

双层复合管是由 2 种不同性能的金属结合而成的一种复合材料，它兼具 2 种组元金属的优良性能，具有高强度、耐腐蚀以及优异的导电、导热等综合性能，因而，越来越多地应用于航空、航天、机械、化工、电力和电子等工业领域。由金属材料制成的双层复合管的生产方式有多种，如拉拔、挤压、爆炸、热轧、离心铸造、连续铸造等。这些方法都已在生产中得到应用，但还存在着产品能耗高、成本高、质量差、环境污染严重、市场竞争力弱等不足，有些方法还存在工序复杂、结合界面的位置和厚度不能精确控制、壁厚不均匀的不足，针对以上不足提出一种新的方法，即多坯料挤压法^[1]，并将此种方法与半固态成形方法^[2] 结合起来。

近几年来，半固态成形技术已成为材料科学领域

的研究热点之一，受到国内外研究人员的普遍重视^[3]。半固态加工技术在美国、意大利、德国和日本等发达国家已经应用到实际生产中，并生产了一些汽车零件和3C产品^[4?5]。但在国内，此项技术目前还在实验室开发阶段，未见有关实际应用的报道。这种方法不仅实现了短流程、近净成形、降低了挤压力^[6]，同时，还能保证生产出的复合管具有优良连接性能，并克服了常规成形方法制备复合管时需二次变形以及复合管内外层均匀性差的缺点。

由于挤压过程中变形材料的流变特征、应力、应变状态等影响挤压制品和挤压模具，同时，挤压模具与工件直接接触也影响挤压制品^[7]，因此，在实际生产中对挤压工艺、挤压模具的结构提出了更高要求。在此，本文作者采用ABAQUS有限元软件对Al/Mg双层复合管热挤压过程进行数值模拟分析，研究挤压速度对变形过程中热力学参数的影响规律；在挤压温度和挤压比不变的情况下，通过数值模拟获得挤压过程中变形材料的应力、应变、温度及流动速度场的分布，为预测快速挤压时加工模具的强度与刚度校核及挤压的缺陷提供依据。

1  热力耦合的原理[1]

在挤压成形过程中，温度对材料变形行为的影响很大，塑性变形与温度场相互影响，进而影响到材料的力学性能，所以，将塑性变形与传热进行耦合分析是非常必要的^[8]。

产生热应力的温度变化可通过结构的热分析计算得出，并将其作为一种载荷，即温度载荷。对于平面应力单元，其等效温度节点载荷为：

将所有单元的变温等效节点载荷叠加在一起，可形成整个结构的所有温度载荷列阵，即，

轴对称是指结构的位移、应变和应力都呈轴对称。针对这一特点，可以简单取出结构的任一子午面进行分析，从而对简化后的平面求解。对于轴对称图形的四节点单元，单元刚度矩阵为：K^e=B^TDbtA，式中t为厚度；A为单元面积。当单元刚度矩阵K^e和{R}^e都已知的情况下，通过刚度矩阵K^e{q}^e={R}^e，可求得节点位移列阵{q}^e，则对应的位移函数为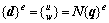：(N为形函数矩阵)；单元应变为：{ε}=B{q}^e；单元应力为：{σ}=DB{q}^{e [9]}。

2  有限元计算

2.1  挤压材料及坯料尺寸

实验材料分2种，其中内部坯料为镁合金AZ91D，外部坯料为铝合金A356。采用这2种合金主要是由于这2种铸造类合金不存在织构的影响，在半固态学  术领域中这2种合金已经得到系统的、广泛的研    究^[10?11]，其化学成分分别见表1和表2。实验所采用的空心AZ91D坯料的外径是20 mm，内径是6 mm；空心A356坯料的外径是50 mm，内径是30 mm；高度均为50 mm。

表1  AZ91D镁合金成分^[10]

Table 1  Nominal compositions of AZ91D alloy (mass fraction, %)

表2  铝合金A356坯料的化学成分^[12]

Table 2  Nominal compositions of A356 alloy (mass fraction, %)

2.2  建模及模拟边界条件

本研究采用多坯料挤压法，所设计的模具为锥模，采用环状坯，挤出的双层管外径为26 mm，壁厚为10 mm。为了适应工程需要，双层复合管需要有不同的界面比，所以，对于壁厚为10 mm的复合管，在此研究中选择3种界面比进行研究，对应的内、外层壁厚比分别为3?7、5?5和7?3，工作带长度为L，分别15、10和5 mm，模型如图1所示。采用图1所示的模型成形时，坯料经过挤压变形后，在接触压力和摩擦力作用下进行焊合，随着温度的降低，接触面位置先固定，随后进行扩散连接。

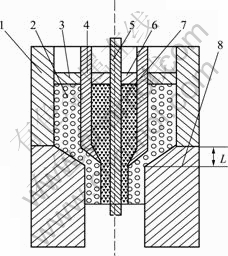
图1  模型原理图

Fig.1  Schematic of model: 1—Outer container; 2—Outer billet; 3—Outer punch; 4—Inner container; 5—Mandrel; 6—Inner punch; 7—Inner billet; 8—Female die

多坯料挤压双层复合管的工艺属于大塑性变形，可以忽略弹性变形。由于材料在成形时处于半固态状态，镁合金和铝合金对变形温度和变形速度比较敏感，通常会表现出一定的粘性，故将镁合金^[10]和铝合金^[3]的材料模型简化为粘塑性模型^[13]。其中A356和AZ91D的本构方程分别来自文献[11]和[10]。考虑到整个成形过程中的热交换很复杂，挤压过程速度较快，在处理边界条件时假设半固态浆料和模具之间的传热方式主要为热传导，成形件与模具之间的对流换热系数保持不变，热辐射折合成对流换热方式。因几何模型轴对称, 在模拟中取其1/2建模。坯料初始网格(半图)的划分如图2所示，单元类型为CAX4RT。当改变界面结合比时，会细化大变形坯料的网格。由于在成形过程中变形相对剧烈，为保证模拟的顺利进行和结果的相对准确性，在模拟中应用网格自适应技术^[14]。挤压筒和挤压模具的初始温度均为300 ℃，镁合金坯料的初始温度(θ_Mg)为580 ℃，铝合金的初始温度(θ_Al)为580 ℃。挤压筒和挤压模上的摩擦因数^[15]均取0.2。

图2  初始网格划分

Fig.2  Initial grids of alloys: A356 (a); AZ91D (b)

3  数值模拟的结果与分析

3.1  不同挤压速度下的温度场

在双层复合管的内、外结合界面比为3?7的情况下，为便于比较，在模拟过程中选定2组速度：①镁合金坯料和铝合金坯料的速度都为0.08 m/s；②镁合金坯料和铝合金坯料的速度都为0.10 m/s，与速度对应的温度场如图3(a)和(b)所示。可以看出，坯料的温度从高到低呈椭圆形向外扩散，形成温度梯度。随着挤压速度的加快，相同位移处的温度逐渐升高。在触变挤压成形过程中，毛坯和加工模具之间强烈的热交换(由热传导和热辐射引起)引起热能损耗。故在实际加工过程中，就需要保证在挤压变形区内，坯料仍然处于半固态温度区间，即变形区总是维持在固?液态，使结合后的坯料总维持在刚刚凝固完的固态。AZ91D的半固态温度区间为502~595 ℃^[10]；A356的半固态温度区间为550~615 ℃^[16]。图3(a)所示的挤压变形区的外表面温度为500 ℃左右，不在最佳半固态温度区间；图3(b)所示的温度为530 ℃左右，在镁合金AZ91D的半固态温度区间，但对于铝合金A356来说已经低于其固相线温度550 ℃，所以，需要进一步加快速度。当速度加快到0.12 m/s时，其温度场如图3(c)的所示，可以看出，A356界面温度已经升高很多，当把铝合金的初始温度提高到590 ℃时，其温度场如图3(d)所示。

以上的模拟结果都是在工作带长度为10 mm的条件下得到的。在①组速度下，当保持界面结合比为3?7时，将工作带长度分别增加到15 mm和减少到5 mm，得到的挤压温度场云图如图3(e)和(g)所示。可见，挤压模的挤压角发生了变化，对应的温度场也发生变化。在相同的位移和速度下，比较图3(e)和(f)中的温度场可知，由于工作带长度加长，挤压变形区的温度降低，增大了挤压阻力，不利于双层复合管的成形。虽然图3(g)所示变形区的温度进一步升高，但是，由于挤压角太大，导致坯料流动受到的阻力增大，坯料的2个表面运行速度差别很大，导致变形更不均匀，以致影响复合管的成形。所以，经过比较得知，适合挤压的工作带长度为10 mm。

图3  不同温度和不同工作带下的温度场

Fig.3  Temperature field of alloys by thixo-co- extrusion with different velocities and working length: (a) L=10 mm, v_Al=v_Mg=0.08 m/s, t=0.2 s; (b) L=10 mm, v_Al=v_Mg=0.10 m/s, t=0.1 s; (c) L=10 mm, v_Al=v_Mg=0.12 m/s, t=0.05 s, θ_Al=580 ℃; (d) L=10 mm, v_Al=v_Mg=0.12 m/s, t=0.05 s, θ_Al=590 ℃; (e) L=15 mm, v_Al=v_Mg=0.08 m/s, t=0.2 s; (f) L=10 mm, v_Al=v_Mg=0.08 m/s, t=0.2 s; (g) L=5 mm, v_Al=v_Mg= 0.08 m/s, t=0.2 s;

图4所示是在4种不同情况下A356铝合金外表面同一节点的温度变化情况。从图4中的曲线1可以看出，当初始温度在580 ℃、挤压速度为0.12 m/s时，经过0.05 s挤压后，A356合金的内表面的温度降低到固相线温度550 ℃左右，而此时2种材料还没有相互接触，所以，要进一步升高合金温度。图4的曲线3所示的是提高镁合金初始温度后的温度变化曲线，经过相同时间后，合金外表面的温度降低到562 ℃，略高于其固相线温度。比较曲线2和3可以看出，当速度由0.10 m/s加快到0.12 m/s后，温降曲线明显变得缓和，经过0.05 s后温度达到558 ℃，所以，坯料经过变形区后温度还处于固相线以上，可以采用此速度。当缩短变形区长度为7 mm时，温度变化如曲线4所示。比较曲线3和4得知，曲线4整体略高于曲线3，表明提温效果不显著，所以，解决A356铝合金外表面温度的最有效途径就是提高其初始温度。对于A356铝合金，当温度提高到590 ℃时，其对应半固态状态下的固相分数接近40%，黏度也进一步降低，触变特点不明显，流变特点发挥主要作用。所以，在此温度下进行的成形拥有流变和触变共同的特点。本着这个原则，铝合金的凸模选定的挤压速度不要小于0.10 m/s，最好为0.12 m/s，镁合金凸模的速度大于0.08 m/s即可。

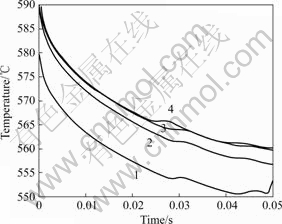
图4  合金A356表面某一节点的温度变化曲线

Fig.4  Temperature curve of one node on surface of A356 alloy: 1—v_Al=v_Mg=0.12 m/s, L=10 mm, θ_Al=580 ℃; 2—v_Al=v_Mg=0.10 m/s, L=10 mm, θ_Al=590 ℃; 3—v_Al=v_Mg=0.12 m/s, L=10 mm, θ_Al=590 ℃; 4—v_Al=v_Mg=0.12 m/s, L=7 mm, θ_Al=590 ℃

3.2  挤压模具的优化

当工作带长度确定后，对挤压模具进行优化。当界面比为3?7时，优化简图如图5所示。把图5(a)所示的内挤压筒的锥模外表面(图中标明的椭圆部位)提高得到的模具如图5(b)所示。比较图5(a)与(b)中坯料的结合情况可以看出，图5(b)所示的结合比图5(a)所示的结合整齐，界面分界线比较直，所以，内挤压筒外表面的锥模长度影响结合面的结合程度。当长度较长时，结合面的质量较好。比较图5(b)和图5(c)可知，外部挤压筒的倒角(图中标明方框的部位)变大，从坯料的流动图可得知，双层复合管的外径与要求的一致，成形良好，所以，外模具的倒角应为10 mm，若太大则不利于复合管的成形；图5(c)与图5(d)所示的是不同速度下的成形图，采用0.10 m/s的速度比0.08 m/s的速度成形出的复合管最下端整齐；图5(e)与图5(d)的不同是，内挤压筒的最下端(图中标明三角的部位)没有被倒角。当下端没有被倒角时，成形图如图5(e)所示，内部坯料运动速度明显高于外部坯料的运动速度，这是由于实际挤压比发生了变化。图5(f)所示为速度提高到0.12 m/s的成形图，与图5(e)相比较没有很大的差别。所以，图5(d)所示的是成形最合适的流动图，其模具参数可供参考，即内模具的外表面锥模(椭圆部位)长于内表面，外模具下端(方框部位)的倒角为10 mm，内模具下端(三角部位)也需要倒圆角。

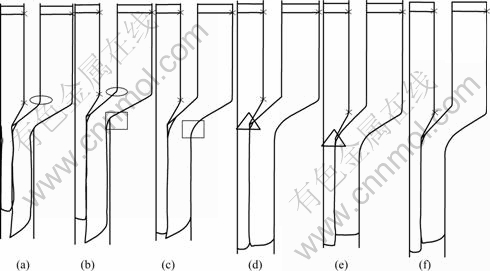
图5  模具和速度优化简图

Fig.5  Optimization of model and speed: (a) v_Al=v_Mg=0.08 m/s, inner billet is not chamfered; (b) v_Al=v_Mg=0.08 m/s, inner billet is chamfered; (c) v_Al=v_Mg=0.08 m/s, out billet is chamfered; (d) v_Al=v_Mg=0.10 m/s, out billet is chamfered; (e) v_Al=v_Mg=0.10 m/s, the bottom of the inner billet is not chamfered; (f) v_Al=v_Mg=0.12 m/s, the bottom of the inner billet is chamfered

3.3  等效应力场和等效应变场

图6所示的是双层复合管的内外结合界面比为3?7，镁合金坯料和铝合金坯料的速度都为0.10 m/s时的应力图和等效应变云图。当2个冲头沿同一方向同时运动时，最大应力分布在工作带区以及坯料与模具接触的区域，这是因为坯料与挤压模具的工作带摩擦产生了较高的剪切应变，这种剪切应变从图6所示的等效应变云图中也可以看出。

图6  应力及等效应变图

Fig.6  Stress (a) and equivalent strain (b)

3.4  不同挤压速度下的速度场

在不同的挤压速度下，对应坯料的速度也不相同，图7所示为在外部坯料上端位移D大约为16 mm，界面结合比为3?7和工作带长度分别为15 mm和10 mm时， 2种速度下形成的速度场关系图。由于挤压比的作用，当初始挤压速度的加快幅度较小时，坯料的速度增快很明显。由于受凹模和挤压筒内壁的摩擦和金属变形温度的影响，靠近凹模和挤压筒内壁的金属流动速度均很小，从而加大了与其他区域金属流动的速度差。在锥模拐角处，镁合金坯料中出现速度很慢的一部分，这部分可形成死区，对成形不利，可能会造成应力集中，所以，模具的挤压角(工作带长度)要进行改善。对比图7(b)与(c)可以得知，随着速度的加快，这部分铝合金的比例逐渐减少。对比图7(a)与(b)，采用10 mm的工作带长度挤压时，速度很慢部分几乎不变，所以，工作带长度可取10 mm。图7(d)所示的是工作带为10 mm时的速度流场图，其中放大部分为工作带处坯料速度的流动方向。所示流动方向分布比较有规律地沿着凹模方向向下，没有涡流现象，缺陷相对较少。

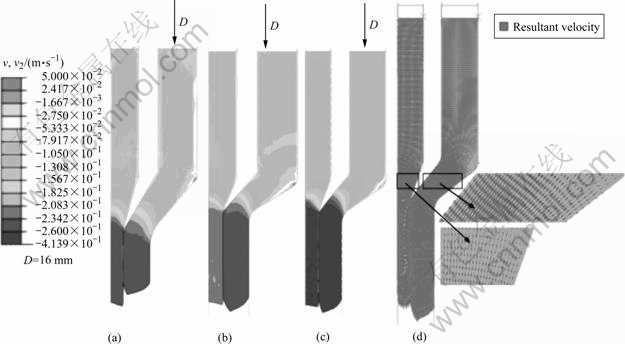
图7  工作带长度15 mm和10 mm时不同挤压速度下的速度场和流场(图中方框处为放大部分)

Fig.7  Flow fields and velocity fields at different speeds: (a) L=15 mm, v_Al=v_Mg=0.08 m/s; (b) L=10 mm, v_Al=v_Mg=0.08 m/s; (c) L=10 mm, v_Al=v_Mg=0.10 m/s; (d) Velocity vector, v_Al=v_Mg=0.08 m/s 

以上模拟都是在结合界面比为3?7的条件下进行的，在实际生产中结合界面比可能发生变化。在此选择内、外结合面比为5?5的情况进行分析，其分析结果如图8(a)所示。可以看出，在镁合金坯料和铝合金的速度为0.10 m/s时，随着时间的进行，2个坯料的差距越来越大，所以，应该加快内部镁合金坯料的速度，但是，会导致在此界面结合比下，不能保证在相同挤压初始速度下成形出界面相对位移小的双层管。图8(b)所示为加快镁合金的挤压速度后的云图，可以看出，2种坯料间还有差距，需要进一步加快镁合金的速度。

当双层复合管的界面结合比变为7?3时，在一定速度下得到的挤压云图如图8(c)和(d)所示。可以看出，在挤压开始阶段变形很均匀，但随着挤压的进行，网格发生很大畸变。其主要原因是两坯料在不同的初始速度下运动，当经过挤压变形区后，慢慢相互接触，但是，由于镁合金坯料的速度比铝合金坯料的速度小很多，阻碍了外部坯料的运动，所以，两者之间产生相对变形。这种变形虽然有摩擦焊合的作用，但是，在两者之间产生的附加应力和残余应力对焊合质量造成严重影响。同时，与外模具接触的坯料由于受摩擦和锥模的作用，运动受到阻碍。所以，上面2个原因导致网格严重畸变。由速度差异造成界面的焊合质量问题需进一步研究。

图8  不同界面比的坯料流动图

Fig.8  Flow of billets by different interface proportions: (a) v_Al=v_Mg=0.10 m/s, t=0.16 s, 5?5; (b) v_Al=0.10 m/s, v_Mg=0.12 m/s, t=0.16 s, 5?5; (c) v_Al=0.09 m/s, v_Mg=0.16 m/s, t=0.09 s, 7?3; (d) v_Al=0.09 m/s, v_Mg=0.16 m/s, t=0.12 s, 7?3;

3.5  结合界面的分析

图9所示为界面结合比为3?7时，在两坯料的外表面选择的2节点沿x向的位移。可以看出，随着时间的进行，2节点的x向位移是水平的，所以，结合面的位置是固定的。根据图中的各个水平坐标值(Max和Min)计算得出对应2种速度下的位移差分别为4.979 1 mm和5 mm，都基本等于内挤压筒的厚度5 mm，所以，结合界面能结合。2种速度下对应同一个节点的2条位移线相差不明显，说明只要模具不变，即使速度加快，结合面的位置还是固定的。

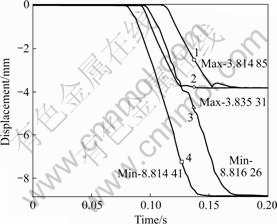
图9  两坯料外边界2节点的x向位移

Fig.9  x-displacement of two nodes on outer boundary of two billets: 1—v_Al=v_Mg=0.10 m/s, U₁ of node on inner billet; 2—v_Al=v_Mg=0.12 m/s, U₁ of node on inner billet; 3—v_Al=v_Mg=0.10 m/s, U₁ of node on outer billet; 4—v_Al=v_Mg=0.12 m/s, U₁ of node on outer billet

结合面之间要实现良好结合，必须要有支持焊合作用的力存在。当界面结合比为3?7，挤压镁合金和铝合金的速度都为0.08 m/s时，两界面间的接触力的变化如图10所示。镁合金坯料和铝合金之间在0.09 s时彼此发生接触，而且两者之间的界面结合处存在接触力，且接触力一直处于震荡状态，在0~10 kN范围内变化，平均值为2 kN左右。该力的存在就证明结合界面间存在接触压力，该力为结合面之间在压力下焊合提供保证，而且该力会随着挤压速度和界面结合比的变化而变化。

图10  两坯料之间的接触力

Fig.10  Contact force between two billets

当界面结合比为3?7时，在两坯料的外表面选择2 个节点，得到2节点的y向位移，如图11所示。两坯料的2个节点在y向的位移，在相同速度下的2条线是平行的，这就证明结合面的2节点的y向距离是不变的，所以，当速度相同时，坯料结合后两者就不再发生相对位移，结合面只是在压力作用下进行焊合，但是当速度不相同时，两坯料的相对滑动距离越来越大，此时结合面间存在压力和摩擦力。当结合面在这2种力下焊合时，关于摩擦力对焊合界面的作用还有待进一步研究。

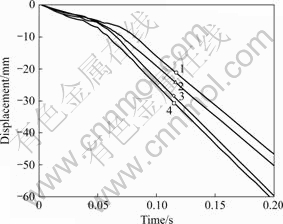
图11  两坯料外边界两节点的y向位移

Fig.11  y-displacement of two nodes on outer boundary of two billets: 1—v_Al=v_Mg=0.10 m/s, U₂ of node on inner billet; 2—v_Al=v_Mg=0.10 m/s, U₂ of node on outer billet; 3—v_Al=v_Mg=0.12 m/s, U₂ of node on inner billet; 4—v_Al=v_Mg=0.12 m/s, U₂ of node on outer billet

4  结论

1) 挤压处于半固态的A356和AZ91D合金，保证A356合金的挤压速度不小于0.10 m/s，最好为0.12 m/s，AZ91D的速度不小于0.08 m/s，A356的初始温度不低于590 ℃，能使两结合面接触后仍处在各自的最佳半固态温度区间。

2) 选择挤压模具的工作带长度为10 mm时，较适合成形双层复合管。

3) 内挤压筒外表面的锥模长度大于内表面的锥模长度，有利于结合面的紧密结合，同时，外挤压筒内表面的锥模末端的倒角应为10 mm左右。

4) 当界面结合比为3?7，且两坯料的挤压速度相同时，结合面的相对位移也为一定值，即界面间只存在压力作用。当两者的速度不一致时，则界面间存在压力和摩擦力的共同作用。

REFERENCES

[1] 谢建新. 材料加工新技术与新工艺[M]. 北京: 冶金工业出版社, 2004.
XIE Jian-xin. Advanced processing technologies of materials[M]. Beijing: Metallurgical Industry Press, 2004.

[2] FLEMING M C. Behavior of metaI alloys in the semi-solid state[J]. Metall Trans, 1991, 22B(6): 270?292.

[3] WANG Kai-kun, KOPP R, HIRT G. Investigation on fracture mechanism of aluminum alloy A356 during thixo-forging[C]// KANG C G. Proc of the 9th S2P. Pusan: Solid State Phoenomena, 2006: 140?144.

[4] AN Lin, KANG Yong-lin, WANG Kai-kun, SUN Jian-lin, XIAO Bang-guo, XU Chen-yang. Low melting point metal semi-solid slurry preparation and microstructure evolution of rheomoulding forming[J]. Journal of Iron and Steel Research International, 2002, 7(suppl.): 407?409.

[5] 罗守靖, 田文彤, 谢水生, 毛卫民. 半固态加工技术及应用[J]. 中国有色金属学报, 2000, 10(6): 765?773.
LUO Shou-jing, TIAN Wen-tong, XIE Shui-sheng, MAO Wei-min. Semi-solid processing technology and application[J]. The Chinese Journal of Nonferrous Metals, 2000, 10(6): 765?773.

[6] LEE B S, JOO D H, KIM M H. Extrusion behavior of Al-Cu alloys in the semisolid state[J]. Materials Science and Engineering A, 2005, 402: 170?176.

[7] 林高用, 周 佳, 张振峰, 郑小燕. 基于DEFORM 2D的纯铜管热挤压过程的数值模拟[J]. 铸造·锻压, 2006, 35(17.): 50?53.
LIN Gao-yong, ZHOU Jia, ZHANG Zhen-feng, ZHENG Xiao-yan. Numerical simulation of hot extrusion of pure copper pipe based on DEFORM 2D[J]. Casting and Forging, 2006, 35(17): 50?53.

[8] ZHANG Heng-hua, XU Luo-ping, SHAO Guang-jie. Finite element simulation on the reheating temperature field of semi-solid A356 aluminum alloy[J]. Transactions of Metal Heat Treatment, 2002, 23(2): 37?41.

[9] 杜平安, 甘娥忠, 于亚婷. 有限元法: 原理、建模及应用[M]. 北京: 国防工业出版社, 2004.
DU Ping-an, GAN E-zhong, YU Ya-ting. The finite element method: The principle, modeling and application[M]. Beijing: Defense Industry Press, 2004.

[10] 谢水生, 李兴刚, 江运喜. 镁合金汽车轮毂半固态触变成形的刚-粘塑性有限元分析[J]. 塑性工程学报, 2005, 12(2): 89?93.
XIE Shui-sheng, LI Xing-gang, JIANG Yun-xi. Rigid-viscous plastic finite element analysis of automobile hubcap of semi-solid thixo-forming of Mg alloy[J]. Journal of Plasticity Engineering, 2005, 12(2): 89?93.

[11] 王开坤, 曾 攀. A356铝合金半固态触变成形过程的有限元模拟[J]. 特种铸造及有色合金, 2007, 27(7): 518?521.
WANG Kai-kun, ZENG Pan. FEM simulation of semi-solid thixo-forming process of A356 alloy[J]. Special Casting and Nonferrous Alloys, 2007, 27(7): 518?521.

[12] 张先念, 张恒华, 邵光杰, 许珞萍, 红 梅. 半固态A356铝合金流变特性研究[J]. 铸造, 2005, 54(1): 44?48.
ZHANG Xian-nian, ZHANG Heng-hua, SHAO Guang-jie, XU Luo-ping, HONG Mei. Investigation on the rheological behavior of semi-solid A356 aluminum alloy[J]. Foundry, 2005, 54(1): 44?48.

[13] KOBAYASHI S, OH S I, ALTAN T. Metal forming and the finite element method[M]. New York: Oxford University Press, 1989.

[14] 庄 茁, 张 帆, 岑 松. ABAQUS非线性有限元分析与实例[M]. 北京: 科学出版社, 2008.
ZHUANG Zhuo, ZHANG Fan, CEN Song. ABAQUS nonlinear FEM analysis and examples[M]. Beijing: Science Press, 2008.

[15] 张朝晖, 廖秋尽, 程荆卫, 王富耻. 双金属复合材料固相结合数值仿真研究[J]. 材料工程, 2006(10): 34?36.
ZHANG Zhao-hui, LIAO Qiu-jin, CHENG Jin-wei, WANG Fu-chi. Numerical simulation to the process of solid phase bonding for Cu/A1 bimeta1 composite by hydrostatic extrusion[J]. Material Engineering, 2006(10): 34?36.

[16] JAFARI M R, ZEBARJAD S M, KOLAHAN F. Simulation of thixoformability of A356 aluminum alloy using ?nite volume method[J]. Mater Sci Eng A, 2007, 454/455: 558?563.

基金项目：北京市自然科学基金资助项目(2072012)；国家高技术研究发展计划(863)资助项目(2007AA03Z119)；中电集团第四十三研究所创新基金项目

收稿日期：2008-07-31；修订日期：2008-11-17

通讯作者：王开坤，博士；E-mail: wkk@mail.tsinghua.edu.cn

(编辑 杨华)