J. Cent. South Univ. (2021) 28: 784-795

DOI: https://doi.org/10.1007/s11771-021-4645-6

Adaptive distributed formation maintenance for multiple UAVs:Exploiting proximity behavior observations

LIU Wei-heng(刘惟恒), ZHENG Xin(郑辛), DENG Zhi-hong(邓志红)

School of Automation, Beijing Institute of Technology, Beijing 100081, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021

Abstract: The formation maintenance of multiple unmanned aerial vehicles (UAVs) based on proximity behavior is explored in this study. Individual decision-making is conducted according to the expected UAV formation structure and the position, velocity, and attitude information of other UAVs in the azimuth area. This resolves problems wherein nodes are necessarily strongly connected and communication is strictly consistent under the traditional distributed formation control method. An adaptive distributed formation flight strategy is established for multiple UAVs by exploiting proximity behavior observations, which remedies the poor flexibility in distributed formation. This technique ensures consistent position and attitude among UAVs. In the proposed method, the azimuth area relative to the UAV itself is established to capture the state information of proximal UAVs. The dependency degree factor is introduced to state update equation based on proximity behavior. Finally, the formation position, speed, and attitude errors are used to form an adaptive dynamic adjustment strategy. Simulations are conducted to demonstrate the effectiveness and robustness of the theoretical results, thus validating the effectiveness of the proposed method.

Key words: unmanned aerial vehicle; formation maintenance; proximity behavior; adaptive distributed control; formation flight control

Cite this article as: LIU Wei-heng, ZHENG Xin, DENG Zhi-hong. Adaptive distributed formation maintenance for multiple UAVs: Exploiting proximity behavior observations [J]. Journal of Central South University, 2021, 28(3): 784-795. DOI: https://doi.org/10.1007/s11771-021-4645-6.

1 Introduction

Unmanned aerial vehicles (UAVs) play an important role in both military and civil fields. Multiple UAVs may be deployed in metal mineral resource exploration, dangerous environment reconnaissance [1], and precise attack tasks [2] to maximize efficiency and prevent the loss of any individual UAV from preventing task completion [3]. Existing multi-UAV formation technologies mainly include collaborative task allocation [4], cooperative path planning [5], communication consensus, collaborative obstacle avoidance [6], and formation maintenance.

Most UAV formation control methods regard the UAV as a mass point, and then create a model based on the multi-UAV topology. WANG et al [7] investigated an inconsistent switching topology to model communication failure among formations, and in an attempt to resolve the problem of non-linear multi-agent systems with switching topology under a leader-follower framework. Other researchers have explored mobile multi-agents using leader-follower formation control as well [8]. A directed graph structure was used to converge to the desired position in the global reference frame [9]. ASKARI et al [10] designed a formation control law according to the inverse dynamics to enhance control accuracy in leader-follower mode. They proposed an improved formation control strategy for virtual structures tailored to the formation flying process. These studies all involved the centralized control method, where there is only one control system computing center in the whole formation [11]. This is not conducive to the large-scale UAV formation system.

In the distributed control context, each UAV has a simple computing center. The whole array of UAVs in formation constitutes a complex and consistent multi-agent system. In many cases, the model parameters of leaders and followers are unknown, so it is difficult to control formation flying with a fixed controller. The distributed output feedback control method is often used for the formation consistency problem with uncertain follower parameters. KURIKI et al [12], for example, built a coordinated formation collision avoidance control strategy based on decentralized model predictive control and consistency theory. REN et al [13, 14] studied formation-keeping and attitude alignment, formation keeping and trajectory tracking, and information consistency in the multi-agent cooperative control context. ZHU et al [15] studied a formation-keeping strategy of multiple UAVs based on consistency in 3D, and adopted a non-linear dynamic inverse design method to restrict the whole formation within the established geometry. However, the UAV formation keeping methods mentioned in the above researches require strict and accurate information exchange.

Other scholars have explored UAV formation control methods as per the social phenomena of biological groups [16, 17]. Behavior consensus is a distributed control method inspired by the behavior of groups of organisms in nature. ZHOU et al [18] designed a close-formation configuration and control method for multiple UAVs that imitates the behavior of wild geese flocks in migration. They built a formation variable topology reconstruction accordingly to realize the formation. They also studied the formation maintenance of multi-UAVs through hybrid particle swarm optimization, genetic algorithm, and modified brain store optimization [19, 20]. Recently, researchers have linked multi- UAV formation control with artificial networks [21], which allows individual UAVs in the network to be autonomously coordinated so as to maintain consistency with the whole formation structure. Most previous studies were conducted under the assumption that the communication topology between individuals in formation is strongly connected or directional [22], which makes the system overly dependent on real-time communication among individuals. When encountering communication interference or communication deception, however, the UAV formation cannot continue to perform the given task.

The present study centers on the problem of obtaining follower feedback information from proximal UAV behavior according to position, velocity, and attitude observations. In the actual engineering environment, it is difficult to obtain accurate dynamic parameters. CHEN et al [23] assumed a constant spanning tree in the union of correlation graphs in a certain time interval, and proposed a linear sampling measurement output feedback controller to achieve full state consistency in a sufficiently small sampling period. ZHAO et al [24] proposed a distributed consistency protocol which solves the consistency problem of linear multi-agent systems on directed graphs of spanning trees by specifying solution times off-line in advance. Distributed predictive control was adopted in this study, inspired by notably unlike previous studies on this subject [25, 26]. The behavior of UAVs in proximity is acquired for dynamic adjustment of the multi-UAV formation, so that the UAV in the space envelope is determined by the proximal UAVs to ensure the structural consistency of the whole system.

In this paper, we aim to provide a multi-UAV formation keeping model considering position, speed and attitude information based on proximity behavior. Firstly, the relative observation azimuth areas of the individual UAV in the formation system is defined to ensure the existence of a dynamic communication topology at any time. Then each UAV uses the neighbor state information to establish the UAV formation tracking protocol, and adopts the distributed predictive control method to minimize the tracking error for a single UAV to formation states. A dynamic position, speed and attitude adjustment strategy is designed for the close flight of UAV formation, in which a single UAV is limited within a certain envelope to keep the formation structure dynamically adjusted according to its current state and neighbor information state, so as to improve the adaptive ability of the whole formation.

The remainder of this paper is organized as follows. In Section 2, we define the azimuth area of each UAV in the multi-UAV system and build a distributed formation model based on their proximity behavior. In Section 3, we propose a dynamic adjustment strategy for frequent maneuvers under formation control accompanied by an error analysis scheme. In Section 4, we give our UAV formation maintenance simulation results, which verify the effectiveness and robustness of the proposed method. In Section 5, we provide conclusions and a brief discussion on future research directions.

2 Formation model establishment

In the actual distributed formation control method, UAV can only accept messages from a limited number of UAVs, and there are communication delays and losses. The UAV can detect the position, speed and attitude of the UAV in the near azimuth area by its own sensor, so as to make up for the communication problems. Assume that the UAV can obtain states from a limited number of UAVs near the azimuth area by means of communication or measurement.

2.1 Definition of azimuth area

The azimuth area of UAV number i is defined to describe the positional relationship among UAVs in the formation, as shown in Figure 1. The coordinate system Oxy of the azimuth area coincides with the body coordinate system O_bx_by_b of the UAV number i. It rotates clockwise along the Ox axis of the UAV number i in the positive direction. Its adjacent environment is divided into m azimuth areas. The position of the adjacent UAV number j relative to the UAV number i is determined according to the angle θ:

i=1, …, n (1)

where Θ_i represents the azimuth area of UAV i and m is a given constant. The surrounding environment information of each UAV in the formation is represented by vectors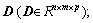n represents the number of UAVs; m represents the number of azimuth areas; and p represents the number of state parameters of the UAVs. For example, represents the k-th parameter in the j-th azimuth region around the i-th UAV.

Figure 1 Proximity azimuth area of the i-th UAV

2.2 Behavior state matrix

Every UAV must be described by nine state parameters in three-dimensional (3D) space, including displacement x, y, z, velocity vector v_x, v_y, v_z, and attitude vector α, β, γ, expressed as vector for the state information of the i-th UAV. There is a coupling relationship in the state parameters [27]. UAV i continuously updates its own status according to the position P_j, velocity V_j and attitude A_j of the j-th UAV for all j≠i, j∈n, so as to maintain consistency with other vehicles in the formation.

The relationship between attitude and position can be expressed as follows:

 (2)

where F_f is decoupling matrix of attitude angle to position vector; and △₁ is the remainder form formation control parameter and input to position. This is expressed as P=F_fA+△₁.

The relationship between attitude and speed is established as follows [28]:

 (3)

where F_g is the decoupling matrix of the attitude angle to the velocity vector; △₂ is the remainder of the current status and location to velocity; and V=F_gA+△₂.

The state transition matrix can be expressed as:

                    (4)

2.3 Formation control parameters

During formation flying, UAVs must maintain a certain distance from each other to prevent collisions. The structure of the formation is determined by vector P_d. The speed of each UAV in the formation needs to be relatively consistent, so speed changes in the formation control parameter vector are determined by the current speed and relative position of proximal UAVs.

The position vector of UAV i relative to the adjacent UAVs is described as follows:

i=1, 2, …, n           (5)

In the whole formation, the individual UAV not only needs to keep a relatively consistent distance from other vehicles but also maintains the proper attitude. The attitude of the formation is determined by vector V_a. The attitude difference between UAV i and its proximal UAVs is expressed as follows:

i=1, 2, …, n           (6)

The formation control parameters vector of UAV i can be described as follows:

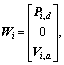i=1, 2 , …, n                   (7)

There are nine state parameters [P, V, A]^T of the UAV in total. There are only four input parameters [△_a, △_r, △_e, △_p]^T, where △_a is the aileron deflection angle; △_r is the rudder deflection angle; △_e is the elevator deflection angle; and △_p is the throttle position. The nine state parameters of the UAV are determined by the four input variables in △u, so the influence of input variables on the UAV state has a coupling relationship [29].

It is assumed that the relationship between the input information and state information of the whole formation satisfies the following:

      (8)

where △₃ is the remainder of control parameters and proximity behavior on the state and [P, V, A]^T=B_h△u+△₃; B_h is the decoupling matrix of state information.

Finally, the control matrix is described as follows:

B=B_h                                                       (9)

2.4 State reference model

As per the above analysis, the state transition matrix and formation control parameters predict the UAV state parameters at the next moment according to the proximity behavior states and formation structures of a limited number of UAVs. The introduction of the state transition matrix and formation control parameters enables the UAV individuals in the whole formation to predict the state information of the next moment according to the behavior state of a limited number of proximal UAVs and the preset formation structure. The state reference model of UAV i is established as follows:

i ≠ j        (10)

i ≠ j, i, j=1, 2, …, n   (11)

where and represent the position, velocity, and attitude of the j-th UAV at time t-1, respectively. denote the estimated states of UAV i at time t according to UAV j. And represent the expected states of UAV i at time t according to the state estimation of m UAVs in the relative azimuth region of UAV i. F represents the state transition matrix; W represents the parameter vector of formation control; B represents the control matrix; and △u is the input parameter. The control input is:

                      (12)

Imprecise sensor measurement, wind disturbance, and limited control stability make it difficult to achieve absolute unity in distance, speed, and attitude among UAVs in the formation flying process. Equation (10) shows that formation- keeping is a dynamic adjustment process considering model error and measurement noise. Equation (11) gives the average estimated optimal state of the i-th UAV as-determined by proximity behavior, which cannot be regarded as the optimal predicted state.

3 Adjustment strategy and error analysis

3.1 State adjustment strategy

UAVs in the azimuth area have different levels of importance. The UAV behavior responsible for formation navigation and maintenance may dominate the UAV behavior of less-important UAVs. To test the proposed method, one or more dependent UAVs in the azimuth region are selected and the dynamic adjustment threshold 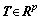is set, where T is the spherical envelope of the p dimension. The spherical envelope center is a point of O_t on the line between the average estimated state center determined by the UAV behavior in the azimuth region and the observation state center of the dependent UAV. This is determined by the distance parameter λ_t (λ∈[0,1]), as shown in Figure 2.

The i-th UAV should be in the state spherical envelope at all times. When the state of the UAV is not in the spherical envelope at time t, it must be dynamically adjusted through the control parameters. When the state of UAV is in the spherical envelope at time t, the UAV only needs to maintain its previous state. The radius of the spherical envelope, R_T, is:

                            (13)

where △_k is the permissible error of the k-th parameter in the p-th state. The i-th UAV in the formation receives the state spherical envelope according to the predicted proximity behavior, judges its current state and its relationship, and then makes a state adjustment decision. Each UAV is restricted within the spherical envelope to keep the formation together.

Figure 2 Status spherical envelope of each UAV in formation

3.2 Error analysis of formation keeping

The behavior of nearby n-1 UAVs impacts any individual UAV in the formation. Theoretically, all UAVs in the azimuth region can be selected as a reference for behavior estimation. There may be errors in the state measurements and observation sensors between UAVs and system errors in the model, however, resulting in an inaccurate state estimation.

The expected position relationship between the i-th UAV and other proximal UAVs in the azimuth area is:

i=1, 2, …, n               (14)

whererepresents the position geometric average value of the i-th UAV predicted through the proximity behavior of UAVs; P_f is a constant vector of the formation keep distance between the i-th UAV preset in the formation and the adjacent UAVs. It is expected that the structure distance between every individual in the formation remains the same throughout the flying process.

The expected speed relationship between the i-th UAV and other adjacent UAVs in the azimuth area is:

i=1, 2, …, n                 (15)

whererepresents the speed geometric average value of the i-th UAV predicted through the proximity behavior of all UAVs; V_f is a constant vector of the speed preset in the formation. It is expected that the speed is consistent between individual UAV in the formation.

The expected attitude relationship between the i-th UAV and other adjacent UAVs in the azimuth area is:

i=1, 2, …, n                (16)

where represents the attitude geometric average value of the i-th UAV predicted from the proximity behavior of all UAVs; A_f is the constant vector of the attitude sequence preset in the formation. It is expected that the attitude of every individual in the formation is consistent.

In the actual formation flying process, measurement noise, limited control accuracy, and limited sensor accuracy create errors in the formation parameter estimation. We considered two primary sources of error in this study, model error and measurement error, which are denoted as σ_m and σ_n, respectively.

There are nine state parameters of every UAV in 3D space that have coupling relationships with the output state [21]. The error rounded-off of higher-order terms on the state parameters is σ_m=[σ_mx, σ_my, σ_mz, σ_mvx, σ_mvy, σ_mvz, σ_mα, σ_mβ, σ_mγ]^T during the linearization of the input value △u. The sensors carried by the UAV have limited accuracy, so noise interference emerges in the measurement. The error of each state parameter is described as σ_n=[σ_nx, σ_ny, σ_nz, σ_nvx, σ_nvy, σ_nvz, σ_nα, σ_nβ, σ_nγ]^T. According to the theory of error synthesis, the estimation error can be expressed as follows:

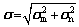                           (17)

4 Simulations and verifications

Adaptive distributed formation flight-keeping technology based on proximity behavior was applied to a variety of formations to test the proposed method. The model predicts the state of individual UAVs based on adjacent UAV behavior. Theoretically, if any UAV’s state changes during the flying process, UAVs adjust themselves in the envelope as-determined by other UAV behavior states according to the measurement information to maintain consistency across the formation. UAVs move at very high speed, so information updates have relatively low frequency and there is a general propensity for collisions between UAVs in the formation. Computers also have limited information-processing speed. In this study, we set the update frequency to △t=0.1 s to reflect real-world conditions.

Six UAVs were distributed on three horizontal planes with height difference h=10 m. The horizontal projection is a triangle with side length L=200 m, as shown in Figure 3. The dynamic adjustment threshold is △=[0.5, 0.6, 0.2, 5, 2, 2, 0.4, 0.2, 0.5]^T in this case and the initial state of each UAV in the formation is T₀=[X₀, Y₀, Z₀, 250, 0, 0, 5, 3, 0]^T, where [X₀, Y₀, Z₀] is any initial position of the UAV. The maximum longitudinal speed of the UAV is V_xmax=360 km/h; the minimum longitudinal speed is V_xmin=180 km/h; the optimal longitudinal speed is V_xopt=288 km/h; the maximum lateral speed is V_ymax=72 km/h; and the maximum vertical speed is V_zmax=54 km/h; the maximum pitch angle α_max=π/4 rad; the maximum yaw angle β_max=π/12 rad; and the maximum roll angle γ_max=π/6 rad.

Figure 3 Formation composed of six UAVs in triangular distribution

Among the six UAVs, the first is responsible for navigation and the fifth is responsible for formation maintenance. In the process of adjusting its current state according to proximity behavior, each UAV has different main-reference UAVs at different reference degrees, as shown in Table 1.

4.1 Position maintenance verification in UAV formation

The dynamic adjustment of the position of each UAV is the premise of normal flight of the multi-UAV formation. Each UAV judges the current position dependence degree according to the proximity behavior given in Table 1, then makes a subsequent prediction. The speed adjustment of the UAV is inherently not very accurate. The speed adjustment error in the x, y, z directions of each iteration is 0.1 times the speed: e_x=e_y=e_z=0.1 m/s. Given the optimal speed of the UAV formation flying, x_opt=288 km/h, y_opt=18 km/h, z_opt=18 km/h, the x-direction-keeping and deviations are shown in Figure 4.

Table 1 Main reference UAVs

Figure 4 x-direction displacement and error of UAVs:

As shown in Figure 4(a), the six UAVs keep consistent in the x-direction according to the formation structure requirements. When t=30 s and t=70 s, the speed of UAV₁ changes and the other five UAVs maintain the proper following behavior. UAV₂ and UAV₃ should always be in the same position in the x-direction. UAV₄, UAV₅ and UAV₆ should also always be in the same position in the x-direction. According to Figure 4(b), the actual position error is consistently below the maximum allowable error when the proposed method is applied. The formation structure is stable and the dynamic consistency between each UAV and the navigational UAV is kept within the allowable error range. As the UAV speed increases, although the distance error between the UAVs in the formation relative to the anticipated error increases, it remains within the allowable maximum error range.

The displacement and error of UAVs in the y-direction are shown in Figure 5. The displacement changes of flight formation in the y-direction are 0, 200, -200 and 0 m. As shown in Figure 5(a), UAV₁ flies according to the given track as other UAVs make maneuvers according to the proximity behavior, and generally keep the proper unified formation. Due to the limited accuracy of position and speed sensors, the near behavior information inevitably causes error accumulation in any decision-making UAV. The introduction of allowable error allows the UAVs to keep formation consistency strategically. As shown in Figure 6(b), when the y-direction speed changes significantly, the y-direction displacement error of the five other UAVs increases relative to UAV₁. When the other five UAVs are flying in formation according to the proximity behavior of the reference UAV (Table 1), the actual y-direction displacement error is consistently below the allowable displacement error △_y=0.6 m.

Figure 5 y-direction displacement and error of UAVs:

The z-direction displacement and error of the UAVs are shown in Figure 6. The navigational UAV₁ moves according to a sine curve as the other UAVs follow perfectly to ensure the stability of the formation. As shown in Figure 6(a), six UAVs are distributed on three levels with a height difference of 10 m. UAV₂ and UAV₃ are relatively close to UAV₁, while UAV₄, UAV₅ and UAV₆ are relatively far away from UAV 1. All five UAVs can maneuver through the proximity behavior specified in Table 1. According to Figure 6(b), the five UAVs maintain the formation and have z-direction error below the allowable level when the formation makes maneuvers. The distance error of UAV₂ and UAV₃, which are close to UAV₁, is slightly smaller than that of UAV₄, UAV₅ and UAV₆, which are farther away from UAV₁.

Figure 6 z-direction displacement and error of UAVs:

In the formation flying experiment on six UAVs, any UAV could make a decision on its expected position in the next moment according to the position behavior of the adjacent UAVs. The position tolerance was satisfied in x-, y- and z-directions.

4.2 Attitude maintenance verification in UAV formation

The attitude following of multi-UAVs according to proximity behavior was also tested by simulation. In each period, the adjustment error of the three attitude angular velocity in this case is 0.1 times the angular velocity, e_α=e_β=e_γ=0.1. The optimal adjusting speeds are α_opt=3°/s, β_opt=2°/s, γ_opt=2°/s, respectively. A smaller allowable error results in smaller attitude error, but the speed then changes dramatically as do the UAV maneuverability requirements. The allowable error of setting attitude is △_α=0.4°, △_β=0.3°, △_γ=1°. The reference UAV sequence is given in Table 1.

As shown in Figure 7(a), during the change of attitude angle α from 0° to 50°, the attitude angle α of the whole formation system maintains strict consistency. When t=50 s, the direction of attitude angular velocity changes and other UAVs follow the proximity behavior specified in Table 1 to change their own state and maintain a uniform formation attitude. As shown in Figure 7(b), during the change of one UAV’s attitude angle α, the changes in the attitude angle α of other UAVs are all within the maximum allowable error △_α=0.4°.

As shown in Figure 8(a), the attitude β of the six-UAV triangle formation is well maintained when changing from -15° to 15°. Other UAVs have high accuracy and effective strategies according to proximity behavior information, and maintain close consistency with the attitude of surrounding UAVs. As shown in Figure 8(b), the minimum error occurs when the change of attitude angular velocity is minimal; the maximum error occurs when the change of attitude angular velocity is maximal. The maximum attitude angle difference between the five other UAVs and UAV₁ is less than the maximum allowable error △_β=0.3°.

As shown in Figure 9, the attitude angle γ of the six-UAV formation is consistent throughout the change in attitude angle γ from -45° to 45°. The attitude error is minimal when the attitude angular velocity changes in the γ direction. The attitude error angle is the largest when the attitude angular velocity changes the fastest, but all indicators are within the maximum allowable error △_γ=1°.

Figure 7 Alpha attitude angle and error of UAVs:

Figure 8 Beta attitude angle and error of UAVs:

Figure 9 Gamma attitude angle and error of UAVs:

The final tracks in x-, y- and z-direction are shown in Figure 10(a). The tracks of all six UAVs are smooth and consecutive and there is no interference in 3D space. The spatial distance is consistent with the initial spatial structure. The final values of three attitude angles of α, β and γ are shown in Figure 10(b). The trajectory lines of the three attitude angles of all six UAVs almost coincide, so the attitude of the UAV formation is unified.

Figure 10 Formation position tracking and attitude angle-keeping of six UAVs:

5 Conclusions

The consistency of distributed multi-UAV formation control is investigated in this study. A formation tracking protocol is established using a limited quantity of proximal UAV state information, and a distributed predictive control method was used to minimize the tracking error of individual UAVs for the whole formation. A dynamic position, velocity, and attitude adjustment strategy is designed to maintain the formation structure, restrict individual UAVs within a given envelope, and enhance the adaptive ability of the whole formation. Simulation results show that the 3D track of each UAV in the formation is smooth and that formation keeping error is within the maximum allowable error range. The proposed adaptive distributed formation keeping method based on proximity behavior is not affected by the initial state of UAVs and is universal and robust. The control scheme is also suitable for the aggregation of UAV formation due to its distributed predictive state-tracking strategy. However, the formation maintenance in the absence of individual observation information yet merits further research.

Contributors

LIU Wei-heng and ZHENG Xin provided the concept and established the models. LIU Wei-heng and DENG Zhi-hong conducted the literature review and performed the theoretical analysis. LIU Wei-heng carried out data acquisition and manuscript editing. ZHENG Xin and DENG Zhi-hong performed manuscript review. All authors have read and approved the content of the manuscript.

Conflict of interest

LIU Wei-heng, ZHENG Xin and DENG Zhi-hong declare that they have no conflict of interest.

References

[1] HE Lü-long, BAI Peng, LIANG Xiao-long, ZHANG Jia-qiang, WANG Wei-jia. Feedback formation control of UAV swarm with multiple implicit leaders [J]. Aerospace Science and Technology, 2018, 72: 327-334. DOI: 10.1016/j.ast.2017.11.020.

[2] YAN Zhe-ping, LIU Yi-bo, YU Chang-bin, ZHOU Jia-jia. Leader-following coordination of multiple UAVs formation under two independent topologies and time-varying delays [J]. Journal of Central South University, 2017, 24(2): 382-393. DOI: 10.1007/s11771-017-3440-x.

[3] WANG Jian-feng, JIA Gao-wei, LIN Jun-can, HOU Zhong-xi. Cooperative task allocation for heterogeneous multi-UAV using multi-objective optimization algorithm [J]. Journal of Central South University, 2020, 27(2): 432-448. DOI: 10.1007/ s11771-020-4307-0.

[4] SCHWARZROCK J, ZACARIAS I, BAZZAN A L C, de ARAUJO F R Q, MOREIRA L H, de FREITAS E P. Solving task allocation problem in multi Unmanned Aerial Vehicles systems using Swarm intelligence [J]. Engineering Applications of Artificial Intelligence, 2018, 72: 10-20. DOI: 10.1016/ j.engappai.2018.03.008.

[5] ROBERGE V, TARBOUCHI M, LABONTE G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning [J]. IEEE Transactions on Industrial Informatics, 2013, 9(1): 132-141. DOI: 10.1109/TII.2012.2198665.

[6] KURIKI Y, NAMERIKAWA T. Consensus-based cooperative formation control with collision avoidance for a multi-UAV system [C]// 2014 American Control Conference. Piscataway, NJ, USA: NUMGE, 2014: 2077-2082.

[7] WANG Jin-liang, WU Huai-ning, Leader-following formation control of multi-agent systems under fixed and switching topologies [J]. International Journal of Control, 2012, 85(6): 695-705. DOI: 10.1080/00207179.2012. 662720.

[8] OH Kwang-kyo, AHN Hyo-sung. Leader-follower type distance-based formation control of a group of autonomous agents [J]. International Journal of Control Automation and Systems, 2017, 15(4): 1738-1745. DOI: 10.1007/s12555- 016-0347-5.

[9] DONG Xi-wang, HUA Yong-zhao, ZHOU Yan, REN Zhang, ZHONG Yi-sheng. Theory and experiment on formation- containment control of multiple multirotor unmanned aerial vehicle systems [J]. IEEE Transactions on Automation Science and Engineering, 2019, 16(1): 229-240. DOI: 10.1109/tase.2018.2792327.

[10] ASKARI A, MORTAZAVI M, TELEBI H A. UAV Formation control via the virtual structure approach [J]. Journal of Aerospace Engineering, 2015, 28(1): 04014047. DOI: 10.1061/(asce)as.1943- 5525.0000351.

[11] HAN Tao, GUAN Zhi-hong, CHI Ming, HU Bing, LI Tao, ZHANG Xian-he. Multi-formation control of nonlinear leader-following multi-agent systems [J]. ISA Transactions, 2017, 69: 140-147. DOI: 10.1016/j.isatra. 2017.05.003.

[12] KURIKI Y, NAMERIKAWA T. Formation control with collision avoidance for a multi-UAV system using decentralized MPC and consensus-based control [C]// 2015 European Control Conference. Piscataway, NJ, USA: NUMGE, 2015: 3079-3084.

[13] REN Wei, BEARD W, ATKIWS E M. Information consensus in multivehicle cooperative control [J]. IEEE Control Systems Magazine, 2007, 27(2): 71-82. DOI: 10.1109/MCS.2007.338264.

[14] REN Wei. Formation keeping and attitude alignment for multiple spacecraft through local interactions [J]. Journal of Guidance, Control, and Dynamics, 2007, 30(2): 633-638. DOI: 10.2514/1.25629.

[15] ZHU Xu, ZHANG Xun-xun, YAN Mao-de, QU Yan-hong. Three-dimensional formation keeping of multi-UAV based on consensus [J]. Journal of Central South University, 2017, 24(6): 1387-1395. DOI: 10.1007/s11771-017-3543-4.

[16] DUAN Hai-bin, QIU Hua-xin. Advancements in pigeon- inspired optimization and its variants [J]. Science China- Information Sciences, 2019, 62(7): 10. DOI: 10.1007/ s11432-018-9752-9.

[17] LWOWSKI J, MAJUMDAR A, BENAVIDEZ P, PREVOST J J, JAMSHIDI M. Bird flocking inspired formation control for unmanned aerial vehicles using stereo camera [J]. IEEE Systems Journal, 2019, 13(3): 3580-3589. DOI: 10.1109/JSYST.2018.2884051.

[18] ZHOU Zi-wei, DUAN Hai-bin, FAN Yan-ming. Unmanned aerial vehicle close formation control based on the behavior mechanism in wild geese [J]. Scientia Sinica Technologica, 2017, 47(3): 230-238. DOI: 10.1360/n006-00138.

[19] DUAN Hai-bin, LUO Qi-nan, SHI Yu-hui, MA Guan-jun. Hybrid particle swarm optimization and genetic algorithm for multi-UAV formation reconfiguration [J]. IEEE Computational Intelligence Magazine, 2013, 8(3): 16-27. DOI: 10.1109/MCI.2013. 2264577.

[20] QIU Hua-xin, DUAN Hai-bin. Receding horizon control for multiple UAV formation flight based on modified brain storm optimization [J]. Nonlinear Dynamics, 2014, 78(3): 1973-1988. DOI: 10.1007/s11071-014-1579-7.

[21] PENG Zhao-xia, WEN Guo-guang, YANG Shi-chun, RANMANI A. Distributed consensus-based formation control for nonholonomic wheeled mobile robots using adaptive neural network [J]. Nonlinear Dynamics, 2016, 86(1): 605-622. DOI: 10.1007/s11071-016-2910-2.

[22] LEE H, EOM S, PARK J, LEE I. UAV-aided secure communications with cooperative jamming [J]. IEEE Transactions on Vehicular Technology, 2018, 67(10): 9385-9392. DOI: 10.1109/tvt.2018.2853723.

[23] CHEN Xi, CHEN Zhi-yong, MEI Cheng-cai. Sampled measurement output feedback control of multi-agent systems with jointly-connected topologies [J]. IEEE Transactions on Automatic Control, 2016, 61(6): 1670-1675. DOI: 10.1109/ TAC.2015.2479113.

[24] ZHAO Yu, LIU Yong-fang, WEN Guang-hui, REN Wei, CHEN Guan-rong. Designing distributed specified-time consensus protocols for linear multiagent systems over directed graphs [J]. IEEE Transactions on Automatic Control, 2019, 64(7): 2945-2952. DOI: 10.1109/TAC.2018.2872534.

[25] WANG Peng, DING Bao-cang. Distributed RHC for tracking and formation of nonholonomic multi-vehicle systems [J]. IEEE Transactions on Automatic Control, 2014, 59(6): 1439-1453. DOI: 10.1109/tac.2014.2304175.

[26] DUNBAR W B, MURRAY R M. Distributed receding horizon control for multi-vehicle formation stabilization [J]. Automatica, 2006, 42(4): 549-558. DOI: 10.1016/ j.automatica.2005.12.008.

[27] HARIKUMAR K, DHALL S, BHAT S. Design and experimental validation of a robust output feedback control for the coupled dynamics of a micro air vehicle [J]. International Journal of Control Automation and Systems, 2019, 17(1): 155-167. DOI: 10.1007/s12555-017-0799-2.

[28] GADEWADIKAR J, LEWIS F, SUBBARAO K, CHEN B M. Attitude control system design for unmanned aerial vehicles using H-infinity and loop-shaping methods [C]// 2007 IEEE International Conference on Control and Automation. 2007: 1174-1179.

[29] SEO J, KIM Y, KIM S, TSOURDOS A. Collision avoidance strategies for unmanned aerial vehicles in formation flight [J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(6): 2718-2734. DOI: 10.1109/TAES.2017. 2714898.

(Edited by ZHENG Yu-tong)

中文导读

基于邻近行为观测方法的多无人机分布式自适应编队控制

摘要：本文研究了基于邻近行为信息状态反馈的多无人机编队队形集结与保持问题。无人机个体根据期望的编队结构以及邻居无人机所在方位角区域的位置、速度和姿态信息进行自主决策，解决了传统分布式编队控制方法中通信拓扑强连通问题和多维度状态信息耦合问题。针对现有分布式编队控制算法中多无人机编队机动灵活性差的问题，以邻近无人机行为信息为观测量建立了一种自适应的分布式编队保持模型。通过已建立的相对方位角区域来获取邻近无人机的状态信息，确保编队中无人机之间位置、速度和姿态的一致性。另外，在邻近行为的状态更新方程中引入关联度因子，利用编队间的位置、速度和姿态误差构成自适应动态调整策略。仿真结果验证了本文所提方法的有效性和鲁棒性。

关键词：无人机；队形保持；邻近行为；自适应分布式控制；编队飞行控制

Received date: 2020-04-20; Accepted date: 2020-11-18

Corresponding author: LIU Wei-heng, PhD; Tel: +86-010-68913798; E-mail: veihenneliu@163.com; ORCID: https://orcid.org/0000- 0003-0484-2929