考虑执行器饱和约束的非光滑船舶航向控制器设计
王国峰,郑凯,王兴成
(大连海事大学 信息科学技术学院,辽宁 大连,116026)
摘要:针对由航向舵工作范围受限引起的饱和约束下船舶航向控制问题,基于非线性系统反步设计思想,结合Filippov微分包含及非光滑系统Lyapunov稳定性理论提出了1种非光滑反馈控制律设计方法。在考虑航向舵执行机构动态的前提下,利用该方法可获得Lipschitz连续的非光滑反馈控制律,并可实现船舶航向控制系统全局渐近稳定性。数值仿真结果验证了该非光滑设计方法的有效性。
关键词:航向控制;饱和非线性;反步设计法;非光滑控制
中图分类号:TP273 文献标志码:A 文章编号:1672-7207(2013)12-4903-07
Nonsmooth controller design of ship steering with saturation
WANG Guofeng, ZHENG Kai, WANG Xingcheng
(Information Science and Technology College, Dalian Maritime University, Dalian 116026, China)
Abstract: In order to overcome the design problem of ship steering control caused by the limited motion of the steering engine, a new nonsmooth feedback control law is developed in this work based on backstepping design method of the nonlinear systems with the consideration of Filippov’s differential inclusion theory and Lyapunov stability theory of the nonsmooth systems. With the mathematical model of the ship steering system including the dynamics of the steering engine, the Lipschitz continuous and nonsmooth feedback controller can be obtained through the proposed design method, which can ensure the globally asymptotic stability of the closed-loop system. The numerical simulation is carried out to verify the nonsmooth control design.
Key words: ship steering; saturation; backstepping design; nonsmooth control
船舶航向控制一直是船舶运动控制所要解决的首要问题之一,其控制的优劣常被作为船舶性能的重要评价指标[1-2]。目前,对该问题的研究主要集中于通过控制舵角来实现航向调整[3-6]。然而,对于浆舵驱动的水面船只,由于航向舵只能在有限范围内工作,这会造成在大角度转向时出现舵角饱和的情况,其将进一步影响航向系统的稳定性[1-3]。传统航向控制器在设计时往往忽略执行机构动态,从而也忽略执行机构具有饱和非线性这一特点,这样得到的控制器往往不能直接应用于实际航向控制问题。实际上,饱和约束条件下航向控制问题可进一步归结为具有饱和非线性的姿态控制问题。魏爱荣等[7]利用Lyapunov方法给出了单输入线性系统状态反馈控制器作用下系统是全局渐近稳定还是区域渐近稳定的充分判据。Francesca等[8-9]针对一类所有状态均受饱和约束的线性系统给出了系统全局渐近稳定的充分必要条件。在控制器设计方面,Anti-windup控制是近年来处理饱和问题常见的手段,其通过利用饱和对象的输入和输出来检测饱和,从而调节控制器增益来实现抗饱和控制[10-12]。这些研究成果普遍关注输入受限控制问题或全部状态受限控制问题。但实际系统饱和特性往往出现在某些执行机构的输出上,而非控制输入受限或全部状态受限,因此,这些结论不能直接应用于饱和约束条件下的船舶航向控制问题。饱和非线性其本质是一种非光滑非线性,其控制问题可从非光滑控制系统理论及设计方法加以考虑[13-16]。本文将针对舵角受限约束条件下的船舶航向控制问题,在设计过程中考虑舵机执行机构动态及受限约束,研究保证船舶航向控制系统获得全局渐近稳定的控制律。首先,基于描述船舶航向动力学的Nomoto模型给出了在饱和约束下采用线性反馈控制的航向控制律。该控制律通过直接调节舵角可获得船舶航向系统大范围渐近稳定。然后,结合非线性系统反步法控制器设计思想,运用Filippov微分包含理论[13]和非光滑系统Lyapunov稳定性理论[14-16]将舵角控制律递推至舵机执行机构,获得了确保整个航向控制系统全局稳定的非光滑反馈控制律。所得控制律含有饱和非线性函数,从而可在一定程度上限制控制器输出,但其又是Lipschitz连续的,因此,不会对执行机构造成不良影响,有利于工程实现。最后,通过仿真实验验证了本文所给控制律的有效性。
1 执行器饱和约束条件下船舶航向控制问题
考虑船舶航向控制问题时,大多数商船可采用Nomoto模型来描述其艏摇运动[1-3],该模型以操纵舵舵角δ为输入,艏摇角ψ为输出,有如下形式:

其中:K1和T1均为正实数,反映船舶操纵性能。由式(1)给出的Nomoto模型可看作是由舵角到艏摇角的船舶航向运动动力学模型。实现时通过舵机驱动舵面获得预定舵角,由于舵机的工作范围往往有限,这使得实际舵角一般在±(25°~35°)范围内,因此在应用式(1)给出船舶航向控制模型时还必须考虑舵角受限因素及舵机动态[1, 3]。用饱和函数描述受限舵角,则模型(1)可写成
 (2)
(2)
其中:饱和函数sat(·)定义为
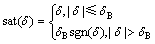 (3)
(3)
δB>0;sgn(·)为符号函数。显然,饱和函数sat(·)是关于自变量非光滑的。
考虑舵机执行机构动态时,一般将其视为简单惯性系统,舵角δ与控制输入u一般具有如下关系:
 (4)
(4)
其中:K2和T2为反映舵机性能的参数,均为正实数。综合船舶航向动力学模型及舵机动态,可得船舶航向运动控制系统的动态模型,即
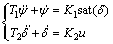 (5)
(5)
式(5)表明控制输入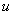 作用下经执行机构到船舶航向输出的动态过程。进一步将其写成状态空间形式为
作用下经执行机构到船舶航向输出的动态过程。进一步将其写成状态空间形式为
 (6)
(6)
其中:状态r为艏摇角速度;状态p为舵角角速度;参数a1=-1/T1,a2=K1/T1,b1=-1/T2及b2=K2/T2。
假设系统状态ψ,r,δ和p已知,预订航向为ψr,则船舶航向控制问题可描述为:设计控制输入u使得实际艏摇角ψ渐近趋近于ψr。取实际艏摇角ψ与预订航向ψr的误差e为新状态变量,则系统(6)可化为
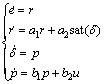 (7)
(7)
这就将船舶航向控制问题转化为四阶系统(7)的镇定控制问题。四阶系统(7)微分方程的右端具有饱和函数,因此,系统(7)为非光滑系统,这使得一般设计方法难以获得可行的控制器。
为解决饱和约束条件下非线性系统(7)的镇定控制问题,下面首先在船舶航向动力学层面考虑舵角控制器的设计,然后利用Filippov微分包含理论和非光滑系统Lyapunov方法将所得舵角控制器推广至舵机执行机构,从而获得舵机饱和约束条件下考虑执行机构动态的船舶航向非光滑反馈控制器。
2 基于Lyapunov方法的非光滑反馈设计
2.1 船舶航向动力学系统状态反馈设计
由于舵角饱和约束仅作用于船舶动力学模型,因此首先考虑船舶航向动力学系统的设计问题有助于整个航向系统的控制设计。在航向动力学层面上,可将上述控制问题描述为如下输入受限系统的镇定问题,即
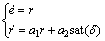 (8)
(8)
其中:舵角δ可被视为系统(8)的受限控制输入,误差e为输出。系统(8)描述的是一个典型的二阶输入受限系统。
为使系统(8)的控制律可被容易地推广至执行机构,不妨采用具有简单形式的线性反馈控制律,即
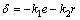 (9)
(9)
其中:设计参数k1和k2均为正实数。下面考虑系统(8)在该控制律作用下系统的稳定性。
对系统(8)进行如下坐标变换:
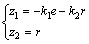 (10)
(10)
其中:z1和z2为该坐标变换下的新状态变量,则系统可由z1和z2表示为
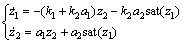 (11)
(11)
为验证系统(11)的稳定性,取正定函数
 (12)
(12)
其中:参数c1和c2为正实数。V1沿系统(11)轨迹的时间导数为
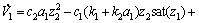
 (13)
(13)
令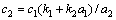 ,根据各参数的符号,有
,根据各参数的符号,有
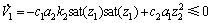 (14)
(14)
故函数V1为Lyapunov函数,系统(11)是全局渐近稳定的。根据坐标变换系统(10)得:当t→∞时,e→0且r→0,故当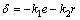 时,系统(8)也是渐近稳定的。这一结论可由如下定理描述。
时,系统(8)也是渐近稳定的。这一结论可由如下定理描述。
定理1:对于由系统(8)描述的输入饱和条件下船舶航向控制问题,存在线性反馈控制律及正实数k1和k2,
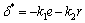 (15)
(15)
使得船舶艏摇角可在任意初始条件下渐近抵达任意预定航向。
定理1的结论表明:对于形如系统(8)给出的二阶输入受限系统,线性状态反馈仍能使系统获得全局渐近稳定。由于线性反馈控制律形式简单,可进一步推广到高阶系统中。下面将针对由系统(7)描述的船舶航向控制问题,在定理1的基础上给出一种基于非光滑反馈的船舶航向控制律。
2.2 基于Lyapunov设计方法的非光滑控制律
执行机构驱动舵面实现舵角指令具有一定的动态过程,因此实际舵角与定理1给出的结果有一定差异。用新状态变量z3表示实际舵角与控制律式(15)给出的舵角指令差异,即
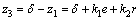 (16)
(16)
将定理1给出的控制律δ*作为虚拟控制,可得z3随时间的变化为
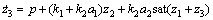 (17)
(17)
以z1,z2和z3作为状态变量的动态系统为
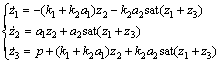 (18)
(18)
显然,将舵角角速度p视为系统(18)的控制输入,可获得在执行机构层面上的部分控制律。
为获得使系统(18)镇定的控制律,取正定函数
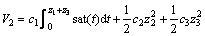 (19)
(19)
其中:c3为正实数。V2沿系统(18)轨迹的时间导数为
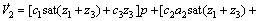
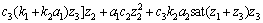 (20)
(20)
取 ,其中设计参数k3>0,k4>0。取合适的c1,c2,k1和k2,使得
,其中设计参数k3>0,k4>0。取合适的c1,c2,k1和k2,使得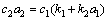 ,则式(20)化为
,则式(20)化为
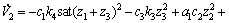
 (21)
(21)
取合适的c3,k3和k4,使得 ,则有
,则有
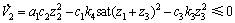 (22)
(22)
故函数V2亦为Lyapunov函数,系统(18)也是全局渐近稳定的。根据状态变量z1,z2和z3的定义可知:当t→∞时,e→0且r→0。
上述推导过程将定理1给出的线性反馈控制律递推至部分执行机构,说明即使系统中存在饱和非线性,利用Lyapunov再设计方法进行递推设计仍是可行的。此递推过程得益于定理1给出的控制律δ*是状态变量的线性组合,可容易获得其关于时间的微分。但p*仅是Lipschitz连续的,其含有饱和函数sat(z1+z3),若将p*作为虚拟控制进一步递推至执行机构的控制输入,就必须考虑因p*不可微而造成的不连续动态对系统的影响。解决这一问题可借助Filippov微分包含理论[13]和非光滑系统Lyapunov稳定性分析方法[14-16]。
令z4表示实际状态p与p*的差异,即
 (23)
(23)
则z4随时间的变化为
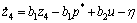 (24)
(24)
其中:η为p*关于时间的导数,η满足[14-15]
 (25)
(25)
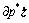 表示p*时间导数所在的集合,其中
表示p*时间导数所在的集合,其中 为p*关于状态变量
为p*关于状态变量 的广义梯度,即
的广义梯度,即
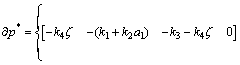
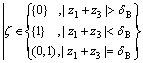 (26)
(26)
由式(26)可知:新状态z4的动态在3个区域有明显变化,这3个区域分别为
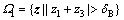 (27)
(27)
 (28)
(28)
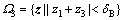 (29)
(29)
其中:区域Ω2可看作是区域Ω1和Ω3的边界。而z4在区域Ω2的动态是不确定的,用Filippov微分包含来描述状态z4及整个系统这种不确定性,可将系统写成如下微分包含形式:
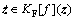 (30)
(30)
式中:KF[f](z)为Filippov微分包含,其满足[13, 16]
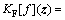
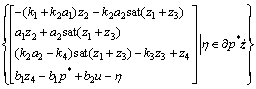 (31)
(31)
显然,原点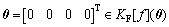 仍为系统(30)的平衡点。微分包含系统(30)描述了原系统在坐标变换(10),(16)及(23)下所得到新系统动态,因坐标系统(23)是非光滑的,故新坐标下系统蕴含因坐标变换引起的不确定性。
仍为系统(30)的平衡点。微分包含系统(30)描述了原系统在坐标变换(10),(16)及(23)下所得到新系统动态,因坐标系统(23)是非光滑的,故新坐标下系统蕴含因坐标变换引起的不确定性。
由式(26)得系统(30)的不确定性为z2,z3,z4及sat(z1+z3)的线性组合,故可设计具有如下形式的控制律u(z1,z2,z3):
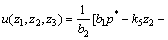
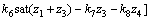 (32)
(32)
其中:k5、k6、k7及k8为设计参数。为确定控制律(32)中的这些设计参数,引入新正定函数
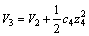 (33)
(33)
其中:c4为正实数。V3沿微分包含系统(30)轨迹的时间导数满足集合[14]
 (34)
(34)
由于V3关于状态变量z可微,故
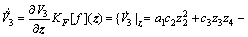
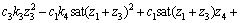
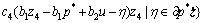 (35)
(35)
将控制律(32)代入式(35),且使设计参数k5,k6和k7满足如下条件:
 (36)
(36)
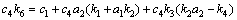 (37)
(37)
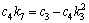 (38)
(38)
则
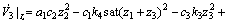
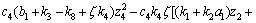
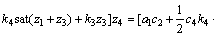
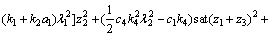
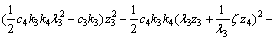
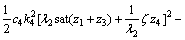
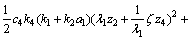
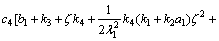
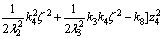 (39)
(39)
其中:参数λ1,λ2和λ3为构造二次多项式时的导出参数。选择适当的数λ1,λ2,λ3,c4和k8使得下列不等式成立:
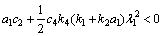 (40)
(40)
 (41)
(41)
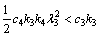 (42)
(42)
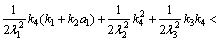
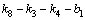 (43)
(43)
又由于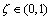 ,则对
,则对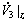 ,显然有
,显然有
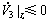 (44)
(44)
由非光滑系统Lyapunov稳定性判定条件可知在控制律(32)作用下,闭环系统是渐近稳定的,且系统渐近收敛于平衡点。该结论可由定理2描述。
定理2:对于由式(7)描述的船舶航向控制问题,存在控制律
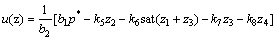 (45)
(45)
其中:zi(i=1,…,4)由式(10),(17)及(23)给定,可通过选择合适的控制参数ki(i=1,…,8),保证船舶航向控制系统全局渐近稳定。
考虑到p*亦为状态变量zi(i=1,…,4),及sat(z1+z3)的线性组合,故控制律(45)也是状态变量及sat(z1+z3)的线性组合。因此,定理2实际给出了一种结合饱和非线性函数及线性状态反馈形式的控制律。这样得到的控制律与p*一样也是状态变量的非光滑Lipschitz连续函数。
此外,上述推导过程也表明:虽然在设计虚拟控制p*时采用了非光滑反馈控制律,会导致在递推过程中出现不连续动态,但仍然可通过连续非光滑反馈控制律进行镇定。这也意味着若船舶航向控制系统或其他含饱和非线性的控制系统具有更高的阶次,也可继续重复上述设计过程,获得使系统全局稳定的连续反馈控制律。这对控制器实现来说,在工程上具有重要的实用价值。
3 仿真研究
取系统参数T1=5,T2=0.5,K1=1,K2=10,δB=20°,航向目标位置为10°,取如下控制参数:
k1=2,k2=4,k3=1,k4=0.6,k5=0.24,
k6=2.44,k7=9,k8=8
对应λ1=λ2=λ3=1。在该组参数下,对Lyapunov函数(33)中参数c1,c2,c3及c4可按如下选取:
c1=0.8,c2=4.8,c3=4.0,c4=0.4
在不同初始条件下分别对定理2给出控制律作用下的闭环系统进行仿真。图1和图2所示为初始条件为ψ0=25°,r0=4,δ0=2及p0=0时航向误差及系统状态r(图2中实线)及p(图2中虚线)的时间响应曲线。由图1和图2可知:系统是渐近稳定的,航向误差可在短时间内收敛至0。图3所示为控制输出u(图3中虚线)及其时间导数(图3中实线)随时间变化的曲线。由图3可知:控制输出u是连续的,而u的时间导数却具有跳变的特点,其在0.44 s和2.16 s附近均发生了向上跳变现象。u的时间导数存在跳变,这说明控制律u是非光滑的。根据控制律(45)是状态变量z1与z3和的非光滑函数,从而也是舵角的非光滑函数。因此,当u的时间导数发生跳变时,实际舵角也将产生非光滑运动。这一点可以从图4中舵角的时间响应曲线得到验证。对比指定舵角输出(图4中虚线)与实际舵角输出(图4中实线),可以发现其也在0.44 s附近进入饱和区域,亦由2.16 s离开饱和区域进入线性工作区,在这2个时刻实际舵角因饱和约束将发生非光滑变化,因控制律中考虑了这一变化,故u的时间导数会在同时刻发生跳变。

图1 航向误差e的时间响应
Fig. 1 Time response of steering error e
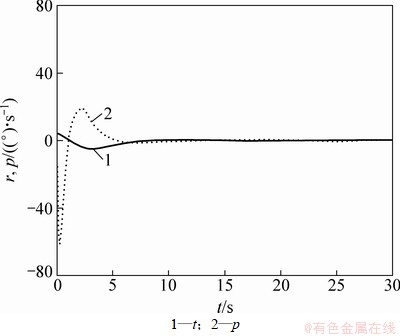
图2 系统状态r和p的时间响应
Fig. 2 Time response of state r and p
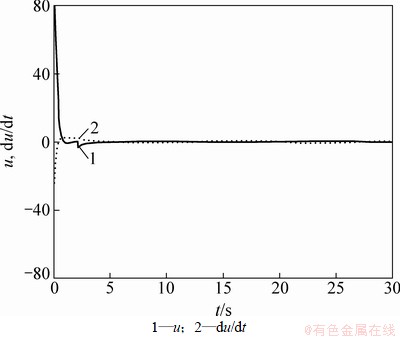
图3 控制输出u及其时间导数
Fig. 3 Control output u and its time derivative 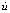
图4 舵角δ的时间响应及其饱和输出
Fig. 4 Time response of rudder angle δ and its saturation
仿真结果也表明:控制律(45)虽然是非光滑的,但并未造成控制器输出和系统状态出现突变,因此,控制结果仍是平缓的,这样的控制器不会对设备造成不良影响,有利于工程实现。
本文设计方法基于反步法设计思想,下面将上述设计结果同一般反步法设计结果进行比较。取定理1中控制律作为反步法的虚拟控制,不考虑舵角饱和,依据反步设计法可获得具有4个设计参数的状态反馈镇定控制律。在数值仿真中,这4个控制参数取为 =2,
=2,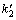 =4,
=4,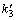 =9,
=9,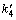 =8,这些参数分别对应定理2中控制器参数k1,k2,k7和k8。初始条件不变,采用反步法所得控制律对系统进行控制所得结果由图5和图6给出(图中实线均为反步法控制律所得结果,虚线均为本文控制律所得结果)。图5所示比较了在二控制器作用下船舶航向误差,二者收敛速度几乎一致。但由图6可知:反步法舵角输出要大于本文方法所得结果,且执行机构饱和时间也略长。这意味着采用本文方法可避免舵机长时间在饱和状态工作。由此可见:与一般反步法相比本文方法不但可确保系统大范围渐近稳定,且能在减少执行机构动作的前提下获得较好的动态性能,从而具有一定的先进性。
=8,这些参数分别对应定理2中控制器参数k1,k2,k7和k8。初始条件不变,采用反步法所得控制律对系统进行控制所得结果由图5和图6给出(图中实线均为反步法控制律所得结果,虚线均为本文控制律所得结果)。图5所示比较了在二控制器作用下船舶航向误差,二者收敛速度几乎一致。但由图6可知:反步法舵角输出要大于本文方法所得结果,且执行机构饱和时间也略长。这意味着采用本文方法可避免舵机长时间在饱和状态工作。由此可见:与一般反步法相比本文方法不但可确保系统大范围渐近稳定,且能在减少执行机构动作的前提下获得较好的动态性能,从而具有一定的先进性。
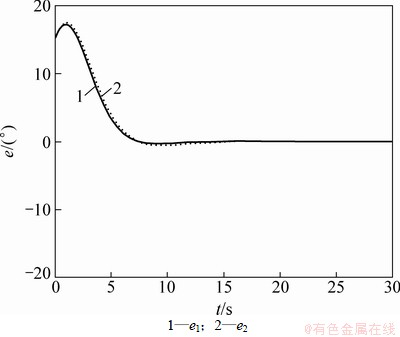
图5 航向误差比较
Fig. 5 Comparison of steering errors
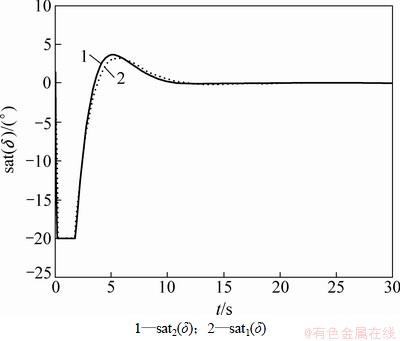
图6 舵角饱和输出比较
Fig. 6 Comparison of saturation outputs of rudder angle
4 结论
(1) 本文研究了舵角饱和约束条件下的船舶航向控制问题,基于非线性系统反步设计法和非光滑系统稳定性理论给出了一种非光滑状态反馈控制器设计方法,从而获得了船舶航向大范围无差控制。
(2) 这种设计方法针对饱和非线性扩展了非线性系统反步设计法,可进一步推广至具有饱和约束的一般高阶系统控制问题的设计中,为解决该类饱和非线性控制问题提供了一条途径。
参考文献:
[1] Fossen T I. Guidance and control of ocean vehicles[M]. New York: Wiley, 1994: 105-114.
[2] 贾欣乐, 杨盐生. 船舶运动数学模型[M]. 大连: 大连海事大学出版社, 1998: 15-35.
JIA Xinle, YANG Yansheng. Mathematical model of ship motion[M]. Dalian, Dalian Maritime University Press, 1998: 15-35.
[3] 杨盐生. 不确定系统的鲁棒控制及其在船舶运动控制系统中的应用[D]. 大连: 大连海事大学, 1999: 72-85.
YANG Yansheng. Robust control for uncertain systems and its applications to ship motion control[D]. Dalian: Dalian Maritime University, 1999: 72-85.
[4] LI Junfang, LI Tieshan, FAN Zhong-zhou et al. Robust adaptive backstepping design for course-keeping control of ship with parameter uncertainty and input saturation[C]//International Conference of Soft Computing and Pattern Recognition. Dalian, China, 2011: 63-67.
[5] 石为人, 邹剑, 宗志亚. 基于反馈线性化的船舶自动舵动态滑模控制[J]. 船舶工程, 2011(5): 50-53.
SHI Weiren, ZOU Jian, ZONG Zhiya. Dynamical sliding mode control of ship autopilot based on feedback linearization[J]. Ship Engineering, 2011(5): 50-53.
[6] 王志文, 彭秀艳. 基于自适应输出反馈的船舶航向控制[J]. 北京理工大学学报, 2011, 31(4): 425-429.
WANG Zhiwen, PENG Xiuyan. Control of ship course based on nn-adaptive output feedback[J]. Transaction of Beijing Institute of Technology, 2011, 31(4): 425-429.
[7] 魏爱荣, 赵克友. 执行器饱和不确定线性系统的分析和设计[J]. 电机与控制学报, 2005, 9(5): 448-451.
WEI Airong, ZHAO Keyou. Analysis and design for single input linear systems subject to input saturation and uncertainty[J]. Electric Machines and Control, 2005, 9(5): 448-451.
[8] Francesca A, Domenico D. Asymptotic stability of continuous-time systems with saturation nonlinearities[J]. Systems & Control Letters, 1996, 29(3): 175-180.
[9] Francesca Albertini, Domenico D’Alessandro, Andrew D. B. Paice. Further conditions on the stability of continuous time systems with saturation[J]. IEEE Transactions on Circuits and Systems—I: Fundamental Theory and Applications, 2000, 47(5): 723-729.
[10] Tarbouriech S, Turner M. Anti-windup design: an overview of some recent advances and open problems[J]. IET control theory & applications, 2009, 3(1): 1-19.
[11] Hu T, Teel A R, Zaccarian L. Anti-windup synthesis for linear control systems with input saturation: Achieving regional, nonlinear performance[J]. Automatica, 2008, 44(2): 512-519.
[12] Tarbouriech S, Turner M. Anti-windup design: An overview of some recent advances and open problems[J]. IET Control Theory & Applications, 2009, 3(1): 1-19.
[13] Filippov A F, Differential equations with discontinuous right-hand side[J]. American Mathematics Society Translation, 1964, 42(2): 199-231.
[14] Paden B E, Sastry S S. A calculus for computing Filippov’s differential inclusion with application to the variable structure control of robot manipulators[J]. IEEE Transactions on Circuits and Systems, 1987, 34(1): 73-82.
[15] Daniel Shevitz, Paden B E. Lyapunov stability theory of nonsmooth systems[J]. IEEE Transactions on Automatic Control, 1994, 39(9): 1910-1914.
[16] ZHENG Kai, SHEN Tielong, YAO Yu. New approaching condition for sliding mode control design with Lipschitz switching surface[J]. Science in China Series F: Information Science, 2009, 52(11): 2032-2044.
(编辑 何运斌)
收稿日期:2012-12-26;修回日期:2013-03-20
基金项目:教育部博士点基金资助项目(20102125120001);国家自然科学基金资助项目(61004007);中央高校基本科研业务费专项资金资助项目(3132013331)
通信作者:郑凯(1981-),男,湖北宜昌人,博士,讲师,从事非线性控制理论、船舶自动控制等研究;电话:18104080900;E-mail:kdmu@ieee.org