DOI:10.19476/j.ysxb.1004.0609.2017.05.019
温度和气压对某金属矿山尾矿坝中毛细水上升规律的影响
章求才1,田亚坤1,张志军1,李亚俊2,刘玄钊3,贺桂成1,刘 永1
(1. 南华大学 核资源工程学院,衡阳 421001;
2. 湖南有色冶金劳动保护研究,长沙 421001;3. 璐安集团,长治 046000)
摘 要:毛细水的存在对尾矿坝的安全稳定有一定影响,而温度、气压的改变会引起毛细水表面张力的变化,进而对尾矿砂中毛细水上升规律产生影响。通过试验模拟尾矿坝中毛细水上升过程,对长期(95 d)毛细水上升过程进行测计,记录当时的温度、气压、时间、上升高度等。建立分别考虑温度、气压及综合考虑温度及气压的毛细水上升规律的分析模型。结果表明:温度对毛细水上升的影响较气压大;在毛细水上升初期,温度、气压对毛细水上升规律的影响不大,但在上升后期其影响逐渐明显。这是由于毛细水上升过程中温度气压对表面张力的影响随着毛细水上升动力逐渐衰减变得显著所致。
关键词:毛细水;尾矿坝;温度;气压
文章编号:1004-0609(2017)-05-1016-07 中图分类号:TU457 文献标志码:A
尾矿坝作为用尾矿砂堆积碾压而成的坝体,其稳定性与其坝体材料尾矿砂的性质密切相关,而由于尾矿砂作为一种土体存在明显的毛细现象,毛细水的存在实质性的改变了土体本身性质,因此,尾矿砂的毛细现象对尾矿坝的稳定性也会有一定影响。2009年, 等[1]采用数值模拟方法研究了尾矿坝稳定性的重要影响因素,开创性地提出水的毛细作用可能会大大降低尾矿坝的安全储备这一论断。据此便需要针对尾矿坝中毛细水运动规律进行研究,而关于土中水的毛细水现象学者们已做了一定研究,如李同录等[2]对黄土中的毛细水上升速度进行现场测试,验证了可用于预测黄土毛细水上升速率的新方法;张志军等[3]分析了某尾矿坝中毛细水的上升规律;王桂尧等[4]通过室内模拟路基水分扩散和冷凝迁移试验,分析了毛细水上升速度变化规律;张文等[5]以青海东部盐渍土为对象,分析了颗粒级配对毛细水上升高度的影响;耿大新等[6]对重塑黏土毛细上升高度进行了研究;刘杰等[7]对毛细作用下的非饱和土路基构建了数值与解析新方法;粟现文等[8]对不同粒径分布粉质黏土毛细水上升试验,探讨了高矿化度潜水地区细粒土质毛细水上升规律;董斌等[9]对12 种不同粗细的土料进行毛细水上升试验,并分析了毛细水上升的影响因素和变化规律;苗强强等[10]以非饱和含黏土砂为研究对象,得出初始含水率对毛细上升高度和上升速度有显著影响的结论;GUO等[11]对粗粒土毛细水上升高度的做了综合测试;杨强义等[12]分析了毛细水干湿循环作用下对土体裂隙发育和强度的影响。然而,总结上述学者们的研究发现,上述研究均未考虑温度和气压对毛细水上升规律的影响。温度和气压的改变会对水的表面张力产生影响,这使得尾矿坝内毛细水的上升情况会受到影响。因此,有必要对尾矿坝中毛细水随温度气压变化规律做进一步研究。
等[1]采用数值模拟方法研究了尾矿坝稳定性的重要影响因素,开创性地提出水的毛细作用可能会大大降低尾矿坝的安全储备这一论断。据此便需要针对尾矿坝中毛细水运动规律进行研究,而关于土中水的毛细水现象学者们已做了一定研究,如李同录等[2]对黄土中的毛细水上升速度进行现场测试,验证了可用于预测黄土毛细水上升速率的新方法;张志军等[3]分析了某尾矿坝中毛细水的上升规律;王桂尧等[4]通过室内模拟路基水分扩散和冷凝迁移试验,分析了毛细水上升速度变化规律;张文等[5]以青海东部盐渍土为对象,分析了颗粒级配对毛细水上升高度的影响;耿大新等[6]对重塑黏土毛细上升高度进行了研究;刘杰等[7]对毛细作用下的非饱和土路基构建了数值与解析新方法;粟现文等[8]对不同粒径分布粉质黏土毛细水上升试验,探讨了高矿化度潜水地区细粒土质毛细水上升规律;董斌等[9]对12 种不同粗细的土料进行毛细水上升试验,并分析了毛细水上升的影响因素和变化规律;苗强强等[10]以非饱和含黏土砂为研究对象,得出初始含水率对毛细上升高度和上升速度有显著影响的结论;GUO等[11]对粗粒土毛细水上升高度的做了综合测试;杨强义等[12]分析了毛细水干湿循环作用下对土体裂隙发育和强度的影响。然而,总结上述学者们的研究发现,上述研究均未考虑温度和气压对毛细水上升规律的影响。温度和气压的改变会对水的表面张力产生影响,这使得尾矿坝内毛细水的上升情况会受到影响。因此,有必要对尾矿坝中毛细水随温度气压变化规律做进一步研究。
1 实验
1.1 试验材料
试验所用的尾矿砂取自湖南省某铅锌矿山尾矿坝(见图1),对所取尾矿砂进行基本的颗粒分析试验,取100~300 g分别过孔径1 mm、0.5 mm、0.25 mm、0.1 mm、0.075 mm的标准筛,共进行30组筛分试验,取其平均值作为最终结果,根据筛分试验结果绘制尾矿砂的颗粒级配曲线(见图2)。按照《土工试验规程》测定原位尾矿砂的部分三相比例指标,颗粒级配参数与物理性质指标见表1,尾矿砂的不均匀系数Cu小于5,曲率系数Cc小于1,该尾矿砂颗粒比较均匀,属级配不良。过2 mm筛后对尾矿砂的矿物组成进行测定,其中以黄铁矿、闪锌矿、毒砂、方铅矿等矿物含量较多,用ICP-MS测定尾矿砂中Fe、Cu、Pb、Zn、Mn、Ni、Ti等主要金属元素含量以及S的含量结果见表2。

图1 试验尾矿砂
Fig. 1 Tailings sample
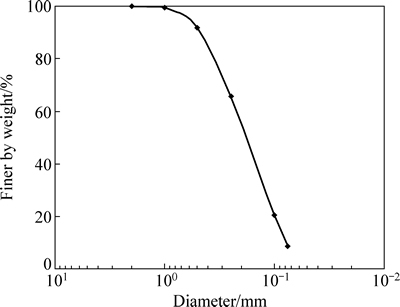
图2 尾矿砂的颗粒级配累计曲线
Fig. 2 Curve of particle size distribution of tailings sand
表1 颗粒级配与主要物理性质指标
Table 1 Particle composition parameters and main physical property indexes of tailings
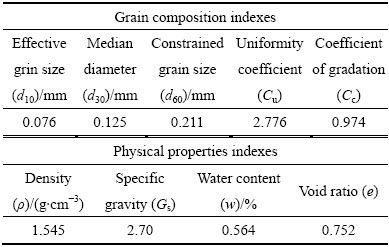
表2 尾矿砂的主要化学元素含量
Table 2 Main chemical element content of tailing sand/%

1.2 毛细水上升试验原理
水与空气的分界面上存在着表面张力,土中的毛细现象就是在表面张力作用下沿着土颗粒间空隙向上及其他方向运动[13]。毛细的湿润现象使毛细管内的水柱弯液面呈内凹,这样便使水柱的表面积增加,在管壁和水分子的引力作用下,使表面积缩小、表面自由能降低,便促使水柱在管内升高,弯液面的形状改变,水柱的升高又改变了弯液面的形状,水和管壁之间的湿润现象又促使水柱面恢复成内凹的弯液面[14-15]。这样不断的循环,使毛细管内的水柱逐渐向上运动至水柱的重力与毛细水上升举力达到平衡状态。
根据向下的水柱重力和管壁与水分子间的引力产生的上举力达到平衡得到理论上毛细水上升最大高度的计算公式:
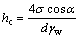 (1)
(1)
式中:hc为毛细水的上升高度,m;σ为水与空气间的表面张力,N/m;α为湿润角,°;d为毛细管的直径,m;γw为水的容重,kN/m3。
1.3 试验方法
按照水利部发布的《土工试验规程SL237—1999》标准,试验采用正水头法直接观测法测定毛细水上升过程,将试验所选尾矿砂自然风干后,称取相同质量的两份,分别装入标号为1号和2号的自制毛细水带分层取样试验装置(见图3)。该装置由内径d=20 cm、高h=15 cm的装置共10层连接而成,管底用土工布封底以防止尾矿砂颗粒流失。两个装置中的尾矿砂密实度相同,将装置竖直固定于水槽中,水槽浸水并保持水槽水位高度为5 cm,同时外部以一定的速度匀速向水槽中持续供水,始终保持水槽中水面刚好没过装置底部5 cm;当高于水槽水位的尾矿砂出现浸润开始计时,并以水槽水面为参考面,同时测记1、2号管的毛细水上升高度,前30 min每隔5 min测记一次,之后随着时间增加,测记间隔时间逐渐延长,每次同时记录当时的温度和气压。经过95 d的持续观测、记录,至毛细水上升达到稳定。

图3 毛细水上升试验装置示意图
Fig. 3 Pictorial diagram of test device of capillary water rising
2 结果与分析
2.1 不考虑温度、气压影响的毛细水上升规律
观测1号管和2号管尾矿砂中毛细水稳定后,1号管毛细水上升最大高度为142.5 cm,2号管为142.6 cm,取1、2号管的相同时间点测定高度的平均值为毛细水上升高度,对毛细水上升高度与时间的关系进行回归分析,通过Microsoft Origin 软件对土水特征曲线的数据进行拟合,发现两段土水特征曲线可以用幂函数很好的拟合。得到回归方程(2),其相关性系数R2=0.9871,置信概率p=0.0153,说明该回归方程具有显著性。对回归方程进行求导,得出其速度方程式(3),毛细水上升高度随时间及上升速度随时间的变化如图4所示。

图4 毛细水上升规律曲线
Fig. 4 Curve of capillary water rising
毛细水上升高度(H)与时间(t)的测记值用幂函数进行回归方程为
H=53.674t0.216 (2)
由式(2)对时间t求导即得尾矿砂中毛细水的上升速度方程:
V=11.594t-0.784 (3)
式中:H为毛细水上升高度,cm;V为毛细水上升速度,cm/d;t为时间,d。
从图4可见,毛细水在开始阶段的上升速度是很快的,随着时间推移,上升速度越来越慢,即毛细水上升相同高度所需的时间越来越多。根据试验过程以及毛细水上升相关理论,分析其原因为:毛细水是在尾矿砂颗粒与水之间的毛细吸力及重力的共同作用下向上运移的,在上升的开始阶段,毛细吸力比重力大得多,所以毛细水上升初期速度很快;但随着毛细水高度的上升,重力逐渐增加,与毛细吸力渐趋平衡,上升的速度就逐渐变慢,当毛细吸力与重力达到平衡时,毛细水停止上升。
2.2 考虑温度、气压影响的毛细水上升规律
温度对表面张力有很直接的影响,这是因为表面张力起源于物体表面分子非对称内聚效应的净吸力,而这种非对称的吸引力又取决于分子间的引力和分子结构,温度变化会直接影响分子的运动。温度升高时由于物质膨胀,分子间距增大,其吸引力减弱,因此一般液体的表面张力都降低;温度降低时,液体的表面张力则增大。关于表面张力和温度的关系式,许多学者研究后都认为二者之间存在线性的关系[15],表3中给出了不同温度时,水与空气间的表面张力值。且气-液两相的净吸力和密度差考虑,气相压力对表面张力是有影响的,且有研究表明,表面张力随压力的增大而减小[16]。
表3 水与空气间的表面张力值
Table 3 Value of surface tension in air-water interface

尾矿库内的库水是暴露在空气中的,因此库水的温度、气压会随着空气温度的变化而变化,库水的表面张力也会随之变化,这使得尾矿坝内毛细水的上升情况会受到影响。为研究温度、气压对毛细水上升规律的影响,笔者在监测毛细水上升的同时测计了当时的气压及温度,测计时间持续95 d,气温气压均有较大变化。
之前分析仅考虑了毛细水上升高度、速度与时间的关系,现加入温度、气压因素,考虑温度、气压因素对尾矿砂中毛细水上升过程的影响。前述中得出幂函数H=53.674t0.216对尾矿砂中毛细水随时间的上升高度回归效果较好,因此将温度的影响加入时间t的指数中。温度用热力学温度表示,符号为T,单位为K。温度的影响用温度比KT来反映,因为温度升高时液体的表面张力降低,所以KT为试验起始时的温度与每一次测记时的温度之比。同样采用幂函数对其进行回归分析,时间和温度与毛细水上升高度之间的回归模型为:
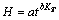 (4)
(4)
式中:KT为起始时刻的温度与t时刻的温度之比;a、b为系数。
回归方程为
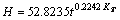 (5)
(5)
气压的影响用气压比KP来反映,因为表面张力随气压的升高而减小,所以KP为试验起始时的气压与每一次测记时的气压之比。建立时间和温度与毛细水上升高度之间的回归模型:
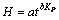 (6)
(6)
式中:H为毛细水上升高度,cm;t为时间,d;KP为起始时刻的气压与t时刻的气压之比;a、b为系数。
回归方程为
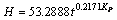 (7)
(7)
同时考虑气温和气压时毛细水的上升情况,将温度、气压的影响共同加入时间t的指数中,则时间、温度和气压与毛细水上升高度之间的回归模型为
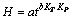 (8)
(8)
回归方程为
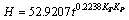 (9)
(9)
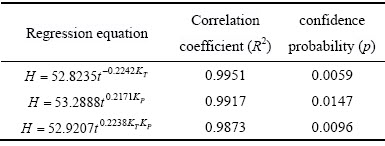
对于回归方程(5)、(7)、(9)的回归结果见表4,相关性系数R2越接近1说明回归方程越显著,置信概率p越小回归方程越显著,回归效果越好。
表4 回归方程的检验统计量
Table 4 The test statistics of regression equation
将式(5)、(7)、(9)分别对时间求导得到分别得到气温、气压、气温及气压影响下的毛细水上升速度表达式(10)、(11)、(12)。
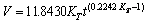 (10)
(10)
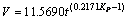 (11)
(11)
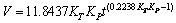 (12)
(12)
考虑当KT或 KP为1,KT且 KP为1,即为气压或温度保持不变时毛细水上升高度与时间的关系,得到关系式(13)、(14)、(15)。
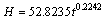 (13)
(13)
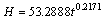 (14)
(14)
 (15)
(15)
对方程(13)、(14)、(15)中时间t求导即得尾矿砂中毛细水的上升速度方程:
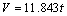 (16)
(16)
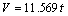 (17)
(17)
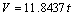 (18)
(18)
绘制(2)、(13)、(14)式的函数图及其对应的毛细水上升速度与时间的关系图如图5所示。
从图5可见,式(13)和式(2)的曲线有比较明显的差别,而式(14)和式(2)的曲线非常接近,这说明温度的变化对毛细水上升高度的影响比气压变化的影响大,温度变化对毛细水上升高度有一定的影响,而气压的变化对毛细水上升高度的影响较微弱。从毛细水上升速度对比发现,温度和气压对毛细水上升速度影响均不明显,但温度对毛细水上升速度的影响较大。
进一步绘制温度、气压综合影响下对尾矿坝中毛细水上升规律和温度、气压均不考虑时尾矿坝中毛细水上升规律如图6所示。
由图6可见,在毛细水上升初期阶段,毛细水上升速度很快,温度和气压对毛细水上升高度及上升速度变化影响均不大,但随着毛细水上升高度增大,从毛细水上升高度与时间的变化图中可看出两种状况下区别逐渐明显。分析认为这是由于毛细水上升过程中毛细上升动力衰减引起的,毛细水是在尾矿砂颗粒与水之间的毛细吸力及重力的共同作用下向上运移,在上升的初始阶段,毛细吸力比重力大得多,毛细上升动力较大,上升速度快,温度气压对表面张力的影响相对毛细上升动力而言很小可以忽略,所以在毛细水上升初期曲线基本重合;但随着毛细水高度的上升,重力逐渐增加,与毛细吸力渐趋平衡,上升的速度也变慢,这时温度气压对表面张力的影响已不能忽略,并成为影响毛细水上升的重要因素之一,致使图中毛细水上升后期两曲线有较大差异。
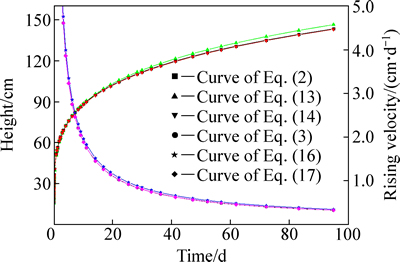
图5 温度或气压影响下毛细水上升规律图
Fig. 5 Curves of capillary water rising influenced by temperature and pressure
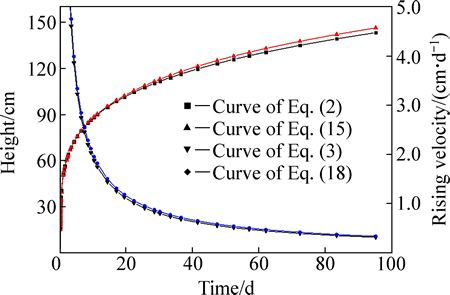
图6 温度、气压综合影响下毛细水上升规律图
Fig. 6 Curves of capillary water rising comprehensive influenced by temperature and pressure
3 结论
1) 尾矿坝中毛细水上升初期速度很快,然后上升速度逐渐变缓,分析采用幂函数对该尾矿砂中毛细水上升高度随时间的变化关系进行回归分析,分别建立了考虑温度、气压及综合考虑温度及气压的毛细水上升规律的幂函数分析模型,分析发现温度对毛细水上升规律影响较气压大。
2) 尾矿砂中毛细水上升初期温度、气压对毛细水上升规律的影响不大,但在上升后期其影响逐渐明显,分析认为是由于毛细水上升过程中上升动力衰减引起的,温度气压对表面张力的影响随着毛细水上升动力逐渐衰减变得显著,成为影响毛细水上升的重要因素。
3) 温度、气压对尾矿砂中的毛细水上升规律均有一定影响,本研究为更全面的分析毛细水运动提供一种新的分析方法,并可作为进一步分析考虑毛细水作用下坝体、边坡、路基等工程的稳定性分析的基础,具有重要的工程应用价值。
REFERENCES
[1]  ZABABAA F. The role of capillary water in the stability of tailing dams[J]. Engineering Geology, 2009, 105(2): 108-118.
ZABABAA F. The role of capillary water in the stability of tailing dams[J]. Engineering Geology, 2009, 105(2): 108-118.
[2] 李 萍, 李同录, 侯晓坤, 牛树轩, 付昱凯, 赵权利. 黄土中毛细上升速率的现场测试[J]. 河海大学学报(自然科学版), 2014, 42(6): 503-507.
LI Ping, LI Tong-lu, HOU Xiao-kun, NIU Xiao-xuan, Fu Yu-kai, ZHAO Quan-li. Field experiment on rate of capillary rise in loess[J]. Journal of Hehai University (Natural Sciences), 2014, 42(6): 503-507.
[3] 张志军, 李亚俊, 刘玄钊, 潘文鑫, 刘 永. 某金属矿山尾矿坝中毛细水上升规律[J]. 中国有色金属学报, 2014, 24(5): 1345-1351.
ZHANG Zhi-jun, LI Ya-jun, LIU Xuan-zhao, PAN Wen-xin, LIU Yong. Rising law of capillary water in tailings dam of metel mine[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(5): 1345-1351.
[4] 王桂尧, 肖 侃, 黄弈茗. 路基土水分扩散和冷凝迁移的室内模拟[J]. 中南大学学报(自然科学版), 2015, 46(12): 4657-4663.
WANG Gui-yao, XIAO Kan, HUANG Yi-ming. Simulation of moisture diffusion and condensate migration in subgrade soil[J]. Journal of Central South University (Science and Technology), 2015, 46(12): 4657-4663.
[5] 魏 凯, 张 文, 刘 昕, 任秀玲, 李生伟, 温 昱. 青海东部盐渍土颗粒级配对毛细水上升影响的研究[J]. 青海大学学报(自然科学版), 2016, 34(3): 1-8.
WEI Kai, ZHANG Wen, LIU Xin, REN Xiu-ling, LI Sheng-wei, WEN Yu. Effects of particle size distribution on capillary water upward movement in saline soil of Eastern Qinghai area[J]. Journal of Qinghai University (Natural Science Edition), 2016, 34(3): 1-8.
[6] 耿大新, 王迎迎, 李宇晗. 重塑黏土毛细上升高度研究[J]. 华东交通大学学报, 2016, 33(2): 100-105.
GEN Da-xin, WANG Ying-ying, LI Yu-han. Study on height of capillary rise for remolded clay[J]. Journal of East China Jiaotong University, 2016, 33(2): 100-105.
[7] 刘 杰, 姚海林, 卢 正, 胡梦玲, 董启朋. 非饱和土路基毛细作用的数值与解析方法研究[J]. 岩土力学, 2013, 34(2): 421-427.
LIU Jie, YAO Hai-lin, LU Zheng, HU Meng-ling, DONG Qi-peng. Study of analytic and numerical methods for capillary action of unsaturated soil-subgrade[J]. Rock and Soil Mechanics, 2013, 34(2): 421-427.
[8] 栗现文, 周金龙, 周念清, 贾瑞亮. 潜水高矿化度对粉质粘土毛细水上升的影响[J]. 干旱区资源与环境, 2016, 30(7): 192-196.
LI Xian-wen, ZHOU Jin-long, ZHOU Nian-qing, JIA Rui-liang. Effects of high TDS on capillary rise of phreatic water in silty clay soil[J]. Journal of Arid Land Resources and Environment, 2016, 30(7): 192-196.
[9] 董 斌, 张喜发, 李 欣, 张冬青. 毛细水上升高度综合试验研究[J]. 岩土工程学报, 2008, 30(10): 1569-1574.
DONG Bin, ZHANG Xi-fa, LI Xin, ZHANG Dong-qing. Comprehensive tests on rising height of capillary water[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(10): 1569-1574.
[10] 苗强强, 陈正汉, 田卿燕, 钱尼贵, 姚志华. 非饱和含黏土砂毛细上升试验研究[J]. 岩土力学, 2011, 32(S1): 327-333.
MIAO Qiang-qiang, CHEN Zheng-han, TIAN Qing-yan, QIAN Ni-gui, YAO Zhi-hua. Experimental study of capillary rise of unsaturated clayey sand[J]. Rock and Soil Mechanics, 2011, 32(S1): 327-333.
[11] GUO Qing-song, LI Xin, LI Min. Comprehensive tests on rising height of capillary water for coarse grained soil[J]. Global Geology, 2013, 16(1): 54-58.
[12] 杨强义, 李承蔚. 毛细水干湿循环对土遗址风化影响试验[J]. 地下空间工程学报, 2012, 8(3): 517-525.
YANG Qiang-yi, LI Cheng-wei. Research on the impact of drying and wetting cycle of capillary water on weathering of soil sites[J]. Chinese Journal of Underground Space and Engineering, 2012, 8(3): 517-525.
[13] 欧阳斌强, 唐朝生, 王德银, 徐士康, 施 斌. 土体水分蒸发研究[J].岩土力学, 2016, 37(3): 625-636.
OUYANG Bin-qiang, TANG Chao-sheng, WANG De-yin, XU Shi-kang, SHI Bin. Advances on soil moisture evaporation[J]. Rock and Soil Mechanics, 2016, 37(3): 625-636.
[14] 张志军, 李亚俊, 贺桂成, 章求才, 韩艳杰, 常 建, 刘玄钊. 某尾矿坝毛细水带内的坝体材料物理力学特性研究[J]. 岩土力学, 2014, 35(6): 1561-1568.
ZHANG Zhi-jun, LI Ya-jun, HE Gui-cheng, ZHANG Qiu-cai, HAN Yan-jie, CHANG Jian, LIU Xuan-zhao. Study on physical and mechanical properties of dam body materials in capillary water fringe of a certain tailings dam[J]. Rock and Soil Mechanics, 2014, 35(6): 1561-1568.
[15] 王少勇, 吴爱祥, 尹升华, 缪秀秀, 胡凯建. 外加电场对细粒散体浸堆渗透性的影响[J]. 中国有色金属学报, 2014, 35(7): 1341-1346.
WANG Shao-yong, WU Ai-xiang, YIN Sheng-hua, MIAO Xiu-xiu, HU Kai-jian. Applied electric field effects on fine particle medium permeability heap leaching[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(5): 1341-1346.
[16] 王少勇, 刘海鹏. 毛细力学[M]. 北京: 科学出版社, 2010.
GAO Shi-qiao, LIU Hai-peng. Capillary mechanics[M]. Beijing: Science Press, 2010.
Influence of temperature and air pressure on rising law of capillary water in tailings dam of metal mine
ZHANG Qiu-cai1, TIAN Ya-kun1, ZHANG Zhi-jun1, LI Ya-jun2, LIU Xuan-zhao3, HE Gui-cheng1, LIU Yong1
(1. School of Nuclear Resources Engineering, University of South China, Hengyang 421001, China;
2. Hunan Nonferrous Metallurgy Labor Protection Research Institute, Changsha 410000, China;
3. Lu’an Group, Changzhi 046000, China)
Abstract: The capillary water will affect on stability of tailings dam, and the surface tension will be changed along with temperature and pressure, which has a great influence on the regularity of the capillary water rising. Therefore, the temperature, pressure time and the height of capillary water rising were tested and recorded during a long term of 95 d. Power function was used to build the analysis model for considering the capillary water rising influenced by temperature and pressure. The results indicate that the temperature has a large impact on the capillary water rising than barometric pressure, and in the early time of capillary water rising, the temperature and air pressure have little effects on it, and in the latter part of capillary water rising, the influence of temperature gradually becomes obvious. Furthermore, the analysis also indicates that the dynamic of capillary water rise gradually decay makes the surface tension influenced by the temperature and air pressure became noticeable.
Key words: capillary water; tailings dam; temperature; pressure
Foundation item: Projects(51004067, 51374129) supported by the National Natural Science Foundation of China; Project(20104324120001) supported by the Research Fund for the Doctoral Program of Higher Education of China; Project(17A184) supported by the Research Foundation of Education Department of Hunan Province, China; Project(2014KS28) supported by the Support Plan for 2014 Social Development Science and Technology of Hengyang City, China; Project(NHCXTD04) supported by the Innovative Team Plan of USC, China; Project (2012XCX22) supported by the Postgraduate Research and Innovation Project of USC, China
Received date: 2016-09-02; Accepted date: 2016-12-09
Corresponding author: ZHANG Zhi-jun; Tel: +86-13575105056; E-mail: zzj181@163.com
(编辑 何学锋)
基金项目:国家自然科学基金资助项目(51004067, 51374129);高等学校博士学科点专项科研基金资助项目(20104324120001);湖南省教育厅重点科研基金资助项目(17A184);衡阳市2014年社会发展科技支撑计划资助项目(2014KS28);南华大学校级创新团队计划资助项目(NHCXTD04);南华大学研究生科研创新项目(2012XCX22)
收稿日期:2016-09-02;修订日期:2016-12-09
通信作者:张志军,博士,教授;电话:13575105056;E-mail:zzj181@163.com