J. Cent. South Univ. (2012) 19: 657-663

DOI: 10.1007/s11771-012-1053-y

Dynamic response law about gravity retaining wall to

seismic characteristics and earth fill properties

LIN Yu-lian(林于廉)^{1, 2}, LIU Yong-jiang(刘涌江)³, LI Jia-jie(李家杰)^{1, 2}

1. College of Urban Construction and Environmental Engineering, Chongqing University, Chongqing 400045, China;

2. Key Laboratory of The Three Gorges Reservoir Region’s Eco-Environment of the Ministry of Education,Chongqing University, Chongqing 400045, China;

3. Transportation Research Institute of Chongqing, Chongqing 400072, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: In order to find the dynamic response laws of retaining walls affected by certain earthquake loads, the influence of the seismic wave characteristics and sub-grade fill parameters (including the foundation surface slope) were focused on, and a series of tests were performed. The results show that the maximum stress of the retaining wall decreases as internal friction angle, foundation slope, filled soil cohesion and the biggest dynamic elastic modulus increase, while it increases with the seismic frequency and seismic input peak dropping. The addition value of dynamics earth pressure increases when seismic frequency and seismic input peak are reduced, while it decreases when the filled soil cohesion and internal friction angle rise. Meanwhile, dynamic elastic modulus and foundation slope have no obvious influences on addition value of dynamics earth pressure. The slope will be instable if the seismic input peak exceeds 0.5g and be disruptive if seismic frequency is larger than 2.5 Hz. The mid-lower parts of retaining walls are in most heavy and obvious response to these factors, which reveals the mechanism of “belly burst” in retaining wall that appears commonly in practical projects.

Key words: retaining wall; earthquake characteristics; earth fill; dynamic response

1 Introduction

Under the effect of earthquake, gravity retaining wall-soil system was prone to slip, tilt, settlement and other failures, and it seriously affected the healthy development of the engineering construction and transportation industry, and brought about great economic loss. Currently, a large number of scholars focused on aspects of analysis methods of soil pressure, fill material and reinforcement of retaining walls and shaking table simulation after Kanto earthquake in 1923, in Japan. In soil pressure analysis methods, it was computed by SUBBA RAO and CHOUDHURY [1] that seismic passive earth pressure coefficients were calculated by the method of limit equilibrium using a pseudo static approach for seismic forces. The upper-bound solutions of the passive earth pressure of static and dynamic force were obtained by means of the kinematical method of the limit analysis theory by SOUBRA [2]. With slip line method and quasi-static method, CHENG [3] and KUMAR [4] derived the earth pressure coefficient of retaining wall under the passive limit state. BENMEBAREK et al [5] analyzed the retaining wall limit of active and passive earth pressure and deformation characteristics of the surrounding soil using finite element. WANG et al [6] and WANG and LIU [7] derived the theoretical calculation method of the size of the dynamic earth pressure, the role of position and dynamic earth pressure distribution. By combining quasi-static limit equilibrium analysis method, YANG et al [8] derived the theoretical formula of the seismic passive earth pressure coefficient, the passive earth pressure force and the role of passive earth pressure force point height when retaining walls and soil interface friction angle were negative. A horizontal slice numerical model method and a retaining wall earthquake failure analysis model and calculation methods were proposed by WANG and BATHURST [9] and YAO [10], respectively. And a cumulative displacement of the computational model was established by WANG et al [11]. In the field of fill material and reinforcement of retaining walls, the seismic behavior of geosynthetic-reinforced soil retaining walls (GRSRWs) after long-term creep was investigated [12-16]. Large model tests were conducted on reinforced gabion walls filled with red sandstone under horizontal seismic loading to investigate the dynamic response of walls by LI et al [17]. In the field of shaking table research, a discrete-continuous power coupled numerical model was used to simulate the seismic response of gravity retaining wall by ZHOU and JIN [18]. Based on rotating block method, the ground vibration velocity threshold was studied by WU et al [19]. With the decoupling numerical simulation of near-field fluctuations in an infinite domain condition, it succeeded in simulating linear elastic waveguide wall-soil processes and deriving the transfer function and ground motion amplification factor by CHEN et al [20-24]. A four-round reinforced earth retaining wall subjected to earthquake loading dynamic behavior was simulated with finite element program by SAMAN et al [25]. However, these studies presented problems of unreasonable model selection and assumptions, while there were few studies about the overall dynamic response of retaining laws. To further study seismic laws of gravity retaining wall, in this work, seismic properties of gravity retaining walls and the dynamic response law of filling characteristics were emphasized on.

2 Model parameters and research programs

2.1 Parameters of model

Section of embankment side slope model is shown in Fig. 1, and section of retaining wall models is shown in Fig. 2. Physical and mechanical parameters of materials are given in Table 1. The retaining walls were placed in a proper position for the purpose of intersection of the top back surface of retaining wall and embankment slope line and intersection of the wall heel of retaining wall and embankment slope line. Accordingly, analysis and calculation were taken on the basis of the established calculation model.

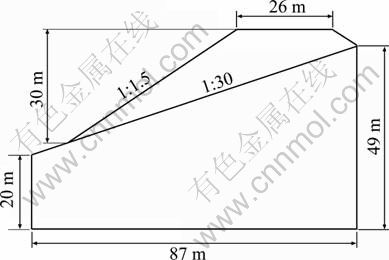
Fig.1 Section of embankment side slope model

2.2 Scheme of method

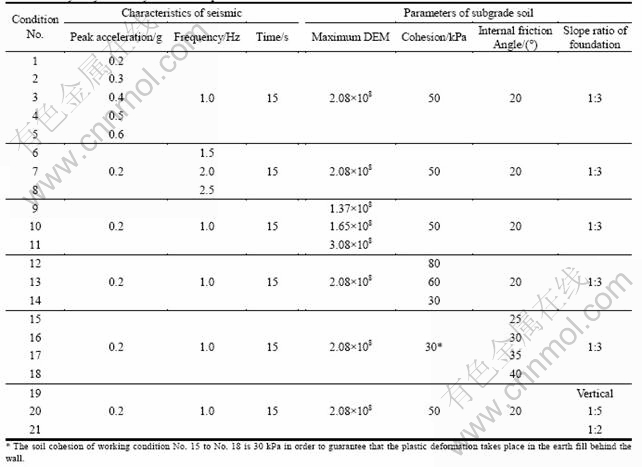
To make a systematic investigation on the law that the characteristics of seismic waves and the parameters of subgrade soil (including slope ratio of foundation surface) affect retaining wall earth pressure, 21 kinds of working conditions were designed, as listed in Table 2. The types of retaining wall are fine-grained soils, and earth-rock mixture packing.

2.3 Calculation method

The maximum resultant stress of the unit (that is, the maximum of the sum of s_xy and s_xx in the condition of element stress considering the normal stress and shear stress behind the wall in the whole dynamic process) and the dynamics earth pressure are designed according to the “Seismic Design of Highway Engineering (JTJ044—89)” [26], using the Coulomb method for embankment retaining wall, shoulder and abutment retaining wall in the same calculation that is the simplified form of Coulomb formula Monobe-Okabe equation.

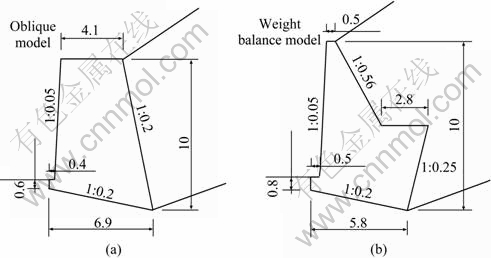
Fig.2 Size of retaining wall models (Unit: m): (a) Oblique retaining wall model; (b) Balance weight retaining wall

Table 1 Physico-mechanical parameters of soil material

Table 2 Analysis system of dynamics earth pressure

3 Dynamic response characteristics of retaining wall

3.1 Effects of earthquake peak on anti-seismic feature of retaining wall

Figure 3 shows the law of resultant stress distribution along the height of wall under the working conditions No. 1-5. According to Fig. 3, joint forces can be worked out. Its amplitude is shown in   Fig. 4 compared with the starting value.

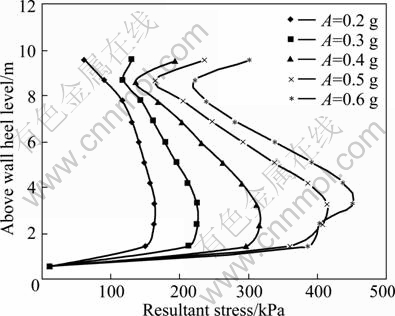
Fig. 3 Resultant stresses corresponding to above wall heel level at different earthquake peak inputs

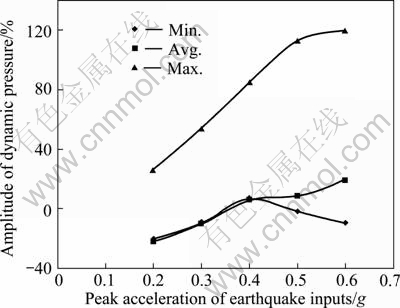
Fig. 4 Amplitude of dynamic pressure corresponding to peak acceleration of earthquake inputs

It can be seen from Fig. 3 that the maximum value of the unit resultant stress increases with increasing the value of the earthquake peak inputs. The most obvious part of the amplitude appears in the mid-lower part of the earth-retaining wall, where the stress exhibits the most intensity. The increase of the wall body pressure and the peak value of it also cause the increase of the amplitude. With the increase of the value of earthquake peak inputs, the earth mass of the top of the wall shows the tendency to lose the stabilization, and the shape does not change assorting with the earth mass behind the bottom wall. In other words, because of the support from the earth-retaining wall, the earth mass behind wall changes little to the free surface, while the earth mass on the top of the wall inclines to destroy independently in the form of shearing above the top, which represents that the units and the stress of the top go up compared with the bottom.

Generally, the amplitude of dynamic earth pressure increases with the ascent of the peak value, especially, its maximum behaves the most obviously. When the peak value is less than 0.5g, the amplitude of the maximum increases linearly with the increase of peak value; when the peak value is above 0.5g, the amplitude can hardly be found, which represents that 0.5g is the critical value of losing stabilization entirely. When the peak value goes above 0.5g, the earth mass is destroyed in the form of shearing above the top, while the influence on the earth pressure of the bottom of wall is limited. For the average value and the final value, some amplitude points are below the zero line, which represents that the average value and the final value are smaller than the starting value. Some facts contribute to this. Firstly, the choice of the starting value has effect on it. And what’s more, the dynamic stress value recorded in the process of the earthquake, even the final one, is also the dynamic stress at the moment that the earthquake response ends, which is not the static earth pressure at the state of equilibrium.

3.2 Effects of earthquake frequency on anti-seismic feature of retaining wall

Figure 5 shows the regular pattern of distribution of resultant stress along the height of the wall, and the relationship between the amplification of the dynamic earth pressure and the earthquake waves is shown in  Fig. 6.

Fig. 5 Resultant stress corresponding to above wall heel level at different frequencies of seismic wave

It can be seen from the analysis of Figs. 5 and 6 that the maximum value of resultant stress of unit increases as the input frequency of the earthquake raises, and that the most obvious range of increase appears in the bottom of the retaining wall. That is to say, as to the distribution of earth pressure in the mass of retaining wall, when the frequency increases, the distributed force increases, and so the increase range of the earth pressure increases. Especially, when the input frequency is 2.5 Hz, the earth pressure increases obviously. Meanwhile, the top of the retaining wall begins to have the tendency of instability as the input frequency of earthquake increases, demonstrating a deformation characteristic inharmonious with the performance of soil mass back the retaining wall. In other words, deformation towards the free surface of the soil mass back the retaining wall is not so obvious because of the retaining of retaining wall. However, as to the top soil mass, the trend of shear failure over the top becomes more and more obvious with the increase of the input peak value of the earthquake, and top-wall units and stress become larger and larger than those on the bottom. The amplification of dynamic earth pressure has almost no variation when the frequency of earthquake is less than 2.0 Hz, but it increases obviously when the frequency exceeds 2.5 Hz, and the variation of maximum value is especially evident. So, it can be seen from the test that the earthquake exhibits obvious damaging effects when its frequency is greater than 2.5 Hz.

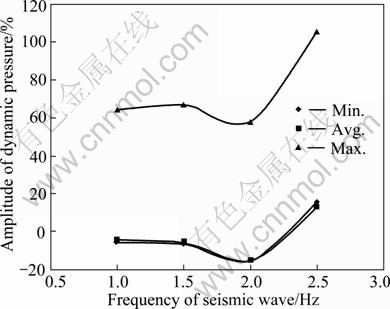
Fig. 6 Amplitude of dynamic pressure corresponding to frequency of seismic wave

3.3 Effects of filler dynamic earth pressure on anti-seismic feature of retaining wall

Figure 7 shows the resultant stress distribution along the height of wall under working conditions No. 1 and No. 9-11. The relationship between the amplification of earth dynamic pressure and the dynamic modulus of elasticity is shown in Fig. 8.

From Fig. 8, it can be known that the maximum resultant stress of the unit decreases as the subgrade dynamic modulus of elasticity increases, and decreasing amplitude is most obvious in the mid-lower part      of retaining wall, but overall drop is not obvious, which means that the impact of foundation soil DEM on earth dynamic pressure is not sensitive.

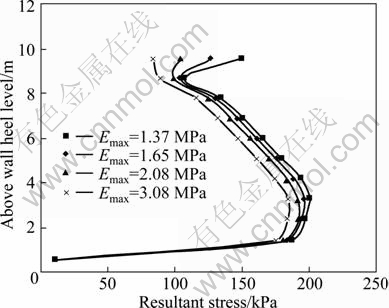
Fig. 7 Resultant stress corresponding to above wall heel level at different dynamic elastic modulus of earth fill

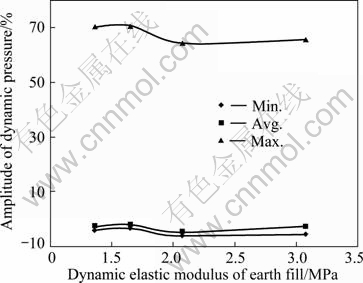
Fig. 8 Amplitude of dynamic pressure corresponding to dynamic elasticity model of earth fill

3.4 Effects of earth fill cohesion on anti-seismic feature of retaining wall

Figure 9 shows the resultant stress distribution along the wall in the form of height under working condition No. 1 and No. 12-14. The amplification compared with the initial value is shown in Fig. 10.

Figures 9-10 show that the maximum resultant stress decreases as the cohesion of the subgrade soil decreases. That’s to say, the pressure in the soil with the cohesion increases. The greater the distribution power is, the greater the pressure drops especially. When the cohesion is 30 kPa, the pressure increases significantly. Generally, with the cohesion decreasing, the amplitude of dynamic pressure increases; especially, when the cohesion is lower than 50 kPa, the amplitude is more obvious.

3.5 Effects of internal friction angle on anti-seismic feature of retaining wall

Figure 11 shows resultant stress distribution of working condition No. 1 (the cohesion is 30 kPa) and working conditions No. 15-18 along the wall in the form of height. The relationship between amplification of dynamic earth pressure and internal friction angle is shown in Fig. 12.

Figures 11 and 12 show that with the internal friction angle of the subgrade soil decreasing, the resultant stress of the unit should increase similarly to the cohesion. The dynamic earth pressure generally increases as the internal friction angle decreases. However, when the internal friction angle is larger than 30°, plastic zone of the slope changes little during the earthquake course. After that, the ground-breaking pressure stays the same.

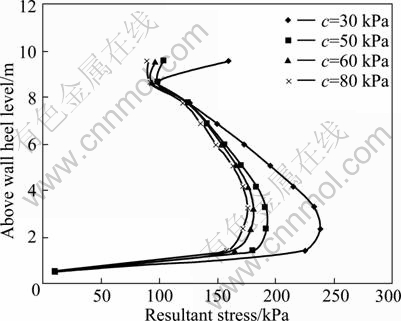
Fig. 9 Resultant stress corresponding to above wall heel level at different cohesion of earth fill

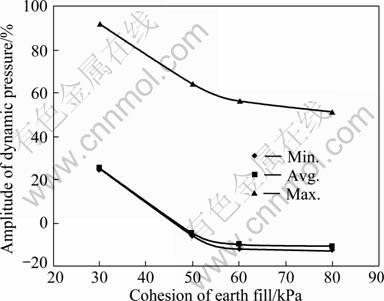
Fig. 10 Amplitude of dynamic pressure corresponding to cohesion of earth fill

3.6 Effects of foundation slope on anti-seismic feature of retaining wall

Figure 13 shows the distribution of resultant stress along the height of the wall under working conditions No. 1 and No. 19-21. Figure 14 shows its amplification compared with the initial value. It can be seen from  Figs. 13 and 14 that with the decrease of the foundation slope, the maximum resultant stress of unit shows an increase trend and the rate of increase appears the most obviously in the middle and bottom of the retaining wall. This suggests that with the increase of the pressure on retaining wall, the slope of foundation and earth pressure show negative correlation.

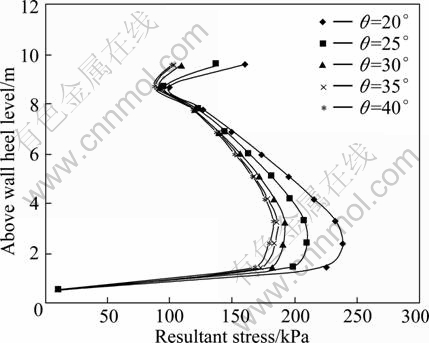
Fig. 11 Resultant stress corresponding to above wall heel level at different internal fraction angles

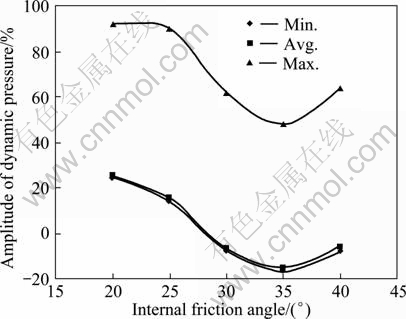
Fig. 12 Amplitude of dynamic pressure corresponding to internal friction angle

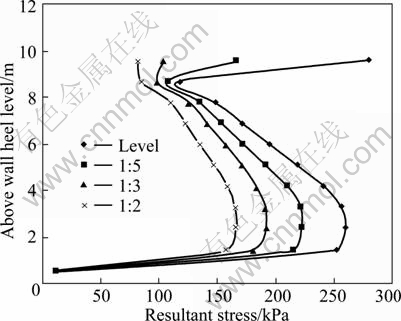
Fig. 13 Resultant stress corresponding to above wall heel level at different foundation slopes

The rate of increase of the soil pressure does not change significantly in general except the level working condition of the foundation. Therefore, the influence on

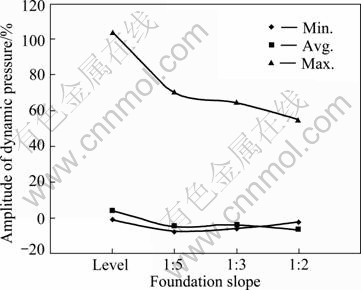
Fig. 14 Amplitude of dynamic pressure corresponding foundation slope

soil pressure of the slope of foundation is mainly reflected by the initial earth pressure. The thicker the filled soil behind the wall is, the greater the level transformation in the compression process is and so is the initial pressure. But, the increase of the dynamic earth pressure during an earthquake is not obvious.

It can be seen from the total results that the reaction of the value on the middle and bottom of the retaining wall is the most significant with the change of the level various factors. This explains why the phenomenon of “belly burst” often appears on retaining wall.

4 Conclusions

1) The maximum resultant stress of the unit increases with the increase of input peak and frequency of the earthquake. With the increase of input peak and frequency, the wall slope has a trend of instability. When the input frequency of the earthquake reaches 2.5 Hz, the dynamic earth pressure increases significantly. The increase amplitude of the dynamic earth pressure increases with increasing the input peak of the earthquake, and the input frequency of the earthquake has no obvious influence on the dynamic earth pressure. But, when the input peak of the earthquake exceeds 0.5 g, the shear breakdown appears in the soil on the top.

2) The maximum resultant stress of the unit increases with increasing the dynamic elastic modulus and the cohesion of subgrade soil. The smaller the dynamic elastic modulus and cohesion of subgrade soil become, the easier the wall top soil turns up failure trend. The dynamic earth pressure of retaining wall increases with decreasing the filled soil cohesion, and dynamic elastic modulus of foundation soil has no obvious influences on the dynamic earth pressure. When the cohesion is less than 50 kPa, the increase amplitude of the dynamic earth pressure is the most obvious.

3) The maximum resultant stress of the unit increases with decreasing the internal friction angle and foundation slope of the foundation soil. The increasing amplitude of the dynamic earth pressure increases with decreasing the internal friction angle, and foundation slope ratio has no obvious influences on the increase amplitude (except the level working condition of foundation). But, the change becomes insignificant when the internal friction angle is more than 30°.

4) The influence of the middle and bottom of the maximum resultant stress of the retaining wall is the most obvious on change of every factor. The mechanism of “belly burst” is revealed in retaining wall that appears commonly in practical projects.

References

[1] SUBBA RAO K S, CHOUDHURY D. Seismic passive earth pressures in soils [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(1): 131-135.

[2] SOUBRA A H. Static and seismic passive earth pressure coefficients on rigid retaining structures [J]. Canadian Geotechnical Journal, 2000, 37: 463-478.

[3] CHENG Y M. Seismic lateral earth pressure coefficients for c-φ soils by slip line method [J]. Computers and Geotechnics, 2003, 30: 661-670.

[4] KUMAR J. Seismic passive earth pressure coefficients for sands [J]. Canadian Geotechnical Journal, 2001, 38: 876-881.

[5] BENMEBAREK S, KHELIFA T, BENMEBAREK S. Numerical evaluation of 3D passive earth pressure coefficients for retaining wall subjected to translation [J]. Computer and Geotechnics, 2008, 35: 47-60.

[6] WANG Li-qiang, WANG Yuan-zhan, CHI Li-hua. Distribution of seismic soil pressure on a retaining wall [J]. China Harbour Engineering, 2007(5): 1-5. (in Chinese)

[7] WANG Li-yan, LIU Han-long. Study of seismic active earth pressure acted on gravity wall in backfill sand [J]. China Journal of Highway and Transport, 2009, 22(6): 26-33.(in Chinese)

[8] YANG Jian, WANG Rong-wen, SHEN Ye, PENG Xiao-jun. Analytical solution of seismic passive earth pressure for negative friction angle of wall-soil interface [J]. Chinese Journal of Geotechnical Engineering, 2011, 33(5): 785-791. (in Chinese)

[9] WANG Yi-min, BATHURST R J. Horizontal slice method for force and displacement analysis of EPS geofoam seismic buffers for rigid retaining walls [J]. China Civil Engineering Journal, 2008, 41(10): 73-80. (in Chinese)

[10] YAO Dun-cheng. Retaining wall seismic failure analysis [J]. Engineering Journal of Wuhan University, 2003, 36(2): 82-87. (in Chinese)

[11] WANG Fu-tao, TAO Xia-xin, DING Lin. Seismic permanent displacement of rigid retaining walls with cohesive backfill [J]. Journal of Shenyang Jianzhu University: Natural Science, 2008, 24(2): 244-247. (in Chinese)

[12] LIU Hua-bei. Internal stability analysis of segmental geosynthetic- reinforced soil retaining walls subjected to seismic loading [J]. Chinese Journal of Geotechnical Engineering, 2008, 30(2): 278-283. (in Chinese)

[13] LIU Hua-bei. Elasto-plastic finite element analysis of geogrid- reinforced sandy soil retaining walls considering effect of creep and earthquake [J]. Chinese Journal of Geotechnical Engineering, 2007, 29(6): 917-921. (in Chinese)

[14] LIU Hua-bei. Analysis on seismic behavior of geogrid-reinforced retaining wall subjected to horizontal and vertical excitation [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(5): 294-299. (in Chinese)

[15] LING Hoe-i, YANG Song-tao, LESHCHINSKY D. Finite-element simulations of full-scale modular-block reinforced soil retaining walls under earthquake loading [J]. Journal of Engineering Mechanics, 2010, 136(5): 653-661.

[16] SOUBRA A H. Static and seismic passive earth pressure coefficients on rigid retaining structures [J]. Canadian Geotechnical Journal, 2000, (37): 463-478.

[17] LI Yun, YANG Guo-lin, LIN Yu-liang. Dynamic characteristics reinforced gabion walls subjected to horizontal seismic loading [J]. Chinese Journal of Geotechnical Engineering, 2009, 31(12): 1930-1935. (in Chinese)

[18] ZHOU Jian, JIN Wei-feng. Coupled approach based numerical simulation of a retaining wall under seismic excitation [J]. Rock and Soil Mechanics, 2010, 31(12): 3949-3957. (in Chinese)

[19] WU Cong-shi, XU Ze-pei, CHEN Xin. Dynamic stability analysis of gravity retaining walls under blast-induced vibration [J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(11): 1939-1942. (in Chinese)

[20] CHEN Xue-liang. Fluctuation simulation analysis of Seismic response of retaining wall [D]. Harbin: Engineering Mechanics Research Institute of China Seismological Bureau, 2001. (in Chinese)

[21] CHEN Xue-liang, YUAN Yi-fan. Explicit integration formula for vibration equation and its accuracy and stability [J]. Earthquake Engineering and Engineering Vibration, 2002, 22(3): 9-14. (in Chinese)

[22] CHEN Xue-liang, YUAN Yi-fan. Fluctuation simulation of Seismic response of retaining wall [C]// Progress of Modern Earthquake Engineering. Nanjing: Southeast University Press, 2002, 266-271. (in Chinese)

[23] YUAN Yi-fan, CHEN Xue-liang. Fluctuation simulation analysis of Seismic response of retaining wall [C]// Earthquake Engineering and Earthquake Preparedness and Disaster Reduction in New Century. Beijing: Earthquake Press, 2002, 585-579. (in Chinese)

[24] CHEN Xue-liang, YUAN Yi-fan. Nonlinear wave propagation simulation of seismic response of retaining wall [J]. Earthquake Engineering and Engineering Vibration, 2003, 23(4): 9-16. (in Chinese)

[25] SAMAN A, BATHURST R J. Numerical modeling of EPS seismic buffer shaking table tests [J]. Geotexiles and Geomembranes, 2008, 26: 371-383.

[26] Highway Planning and Design Institute of the Ministry of Communications. Anti-seismic design code for highway engineering. JTJ 004-1989 [S]. Beijing: China Communications Press, 1989.

(Edited by YANG Bing)

Foundation item: Project(2006-318-740-20) supported by the West Project from the Department of Transportation of China

Received date: 2011-07-26; Accepted date: 2011-11-14

Corresponding author: LIN Yu-lian, PhD; Tel: +86-15089021595; E-mail: goodjy888@sina.com