文章编号: 1004-0609(2006)10-1678-06
含两种尺度微裂纹的高强铝合金的断裂韧性模型
陈康华, 齐雄伟, 宋 旼
(中南大学 粉末冶金国家重点实验室, 长沙 410083)
摘 要: 基于高强铝合金在断裂过程中萌生不同尺度微裂纹的机制, 用断裂力学建立两种尺度微裂纹影响应力应变场的规律, 导出高强铝合金拉伸延性与两种尺度微裂纹的关系, 由断裂韧性与拉伸延性的关系建立了高强铝合金断裂韧性与双级微裂纹的非线性关系模型。 通过模型解析, 分析两种尺度微裂纹体积分数对高强铝合金断裂韧性的影响规律。 结果表明: 随着一级微裂纹体积分数的增加, 材料的断裂韧性开始迅速下降, 然后缓慢降低; 在较大尺度微裂纹之间萌生小尺度微裂纹, 将显著降低合金的断裂韧性。 将高强铝合金的结晶相作为一级微裂纹, 将弥散相和粗大析出相作为二级微裂纹, 预测高强铝合金断裂韧性随两种尺度相(微裂纹)的变化, 其规律与实验结果较为吻合。 利用模型解析与实验验证结果, 提出了改善高强铝合金断裂韧性的组织控制方向。
关键词: 铝合金; 断裂韧性; 模型; 变形; 断裂
中图分类号: TG249.9 文献标识码: A
Model of fracture toughness for high-strength aluminum alloy containing two-scale-size microcracks
CHEN Kang-hua, QI Xiong-wei, SONG Min
(State Key Laboratory of Powder Metallurgy,
Central South University, Changsha 410083, China)
Abstract: A fracture toughness model of high-strength aluminum alloy was established to describe the nonlinear relationship between fracture toughness and two-scale-size microcracks, based on fracture mechanics of two-scale-size microcracks initiated during aluminum alloy deformation and the derived relation between tensile ductility and two-scale-size microcracks. The model shows the effect of volume fraction of two-scale-size microcracks on fracture toughness of aluminum alloy. The fracture toughness of aluminum alloy decreases dramatically and then decreases moderately with the increase of large-scale-size microcracks. The formation of the small-scale size microcracks between the large microcracks decrease the fracture toughness sharply. The model predictions of the fracture toughness evolution of high-strength aluminum alloys with two-scale-size microcracks agree with the experimental data, with the constituents being large-scale-size microcracks and the coarse dispersoids and precipitates being small-scale size microcracks. How to improve fracture toughness of high-strength aluminum alloy was discussed based on this model.
Key words: aluminum alloy; fracture toughness; model; deformation; fracture
航空航天等高技术领域的发展对高强铝合金的强度、 韧性等综合性能不断提出更高的要求。 按照各种场合的应用要求, 优化高强铝合金的综合性能是高强铝合金研究面临的重要课题。 一般来说, 铝合金的强度和韧性是相互矛盾、 此消彼长的两个方面。 如何使高强铝合金的强度和韧性得到合理优化, 是令人非常关注, 又未很好解决的难题。 这要求建立高强铝合金强韧性与其多相组织的定量关系。 为了了解和掌握高强合金微观损伤对断裂韧性的影响, 人们已进行了大量的实验研究工作[1-8]。 但高强合金多相组织参数及其损伤对强韧性的理论研究及定量实验研究较少。 Chan等[9]研究了含氢化物Zr-Ti合金的形变断裂模型, 以易脆断的氢化物为内裂纹, 分析了裂纹前端以及相邻裂纹间基体韧带内的应力应变场, 建立了合金宏观断裂应变与韧带微观塑性应变关联的拉伸延性模型。 在以往金属材料韧性断裂的研究中, 均将塑性变形过程中材料内部微空洞的萌生、 长大及其聚合失稳机制作为在微观尺度水平上表征材料断裂韧性的单一研究对象, 因此描叙微空洞演变行为以及诱发空洞的同一尺度量级的夹杂物的变量便成为相应表达式中的主要参数。 刘刚等[10] 综合考虑了不同尺度第二相在拉伸断裂过程中各自的作用机制, 以粗大的结晶相为内裂纹, 以尺度较小的弥散相和析出相为强化相, 运用位错理论与塑性梯度理论导出了韧带微观塑性应变表达式, 建立了高强铝合金的断裂韧性模型。
但从金属材料断口表面可以观察到连接大韧窝的一系列小韧窝。 一般来说, 合金材料在外力作用下, 同一量级的夹杂物早期断裂构成初始裂纹源(即一级微裂纹); 随着应变的加剧, 处于一级微裂纹之间韧带区很容易萌生微空洞, 形成二级微裂纹。 伴随着一级微裂纹的长大及其与二级微裂纹的连通, 材料随即产生断裂[11, 12]。 前人已经建立了一级微裂纹影响材料断裂韧性的模型, 但尚未见到反映二种尺度微裂纹同时并存影响材料断裂韧性的模型。 为了更好地理解各种因素对断裂韧性的多元非线性影响, 本文作者试图在已建立的一级微裂纹对材料断裂韧性影响的基础上, 进一步考虑二级微裂纹的作用, 建立材料两级微裂纹形成与断裂韧性的关系模型, 并结合实验结果对该模型的预测结果进行验证。
1 模型
材料在加载过程中, 同一尺度量级的脆性夹杂物A很容易先期断裂, 产生一级微裂纹, 随着应变的加剧, 在相邻两微裂纹之间的韧带区很容易萌生微空洞, 产生二级微裂纹B。 假定微裂纹A以立方结构周期性分布, m个裂纹B均匀分布在微裂纹A之间的韧带区内(见图1)。
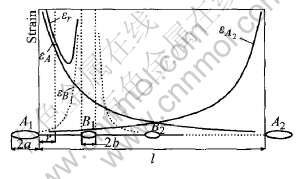
图1 断裂韧性模型的示意图
Fig.1 Schematic diagram of model for fracture toughness
材料加载时, 由于一级微裂纹A1和A2的存在, 距裂纹尖端r处产生的应变可表示为[13-15]:

材料加载时, 由于二级微裂纹B1, B2, …, Bm的存在, 分别在r处产生的应变表达式为

联立方程式(1)~(3), 即所有分级微裂纹在韧带上各自形成的微观应力应变场相互叠加, 得到一 个新的局部应力应变场:
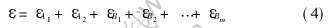
则试样的宏观塑性应变可通过对韧带内微观塑性应变的解析分析获得:
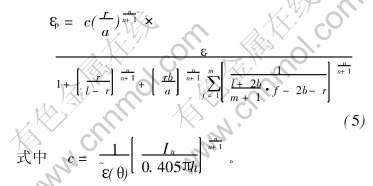
当裂纹前端的张开位移δ达到临界值δc, 此时r处的微观塑性应变εr达到基体断裂应变εc, 裂纹开始扩展, 并失稳连通, 导致材料断裂, 则

从唯象表达的角度, 材料断裂韧性KIC与主裂纹尖端临界应变密切相关[21], 可表示为

式中 D为约等于0.025的常量; ε*C为裂纹尖端的临界应变; v为泊松比。
对于ε*C与εf之间的大致关系, 不论是理论分析还是实验结果[21], 都证实了ε*C近似等于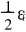 , 由此联立式(6)和(7)可得到断裂韧性的表达式:
, 由此联立式(6)和(7)可得到断裂韧性的表达式:
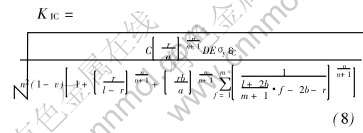
若定义(KIC)R为参考断裂应变, 并把n看作一个常数, 用KIC除以(KIC)R, 可得到约化的材料断裂韧性比R。
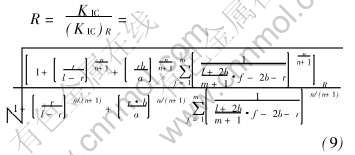
2 模型解析与讨论
2.1 一级微裂纹对材料断裂韧性的影响
模型中的一级微裂纹和二级微裂纹是相对的。 当材料中只有一级微裂纹, 不存在二级微裂纹(b=0), 由式(8)可推导得到材料的断裂韧性表达式:
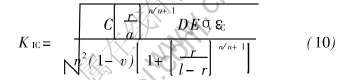
取含0.01%一级微裂纹体积分数的材料为参考态, r=20μm, 得到材料的相对断裂韧性R(一级微裂纹的体积分数由公式φ=2πKa3/(l+2a)3来确定, 式中K为一级微裂纹的形状因子, 取为1)。 从图2可以看出, 随着一级微裂纹体积分数的增加, 材料的断裂韧性开始迅速下降, 然后缓慢降低。
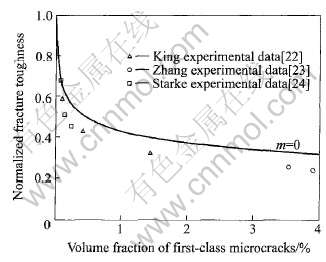
图2 一级微裂纹对材料断裂韧性的影响
Fig.2 Effect of first-class microcracks on fracture toughness
在高强铝合金中, 结晶相在合金的加工过程中断裂或在外载荷作用下断裂形成一级微裂纹。 结晶相越多, 一级微裂纹越多, 铝合金韧性越差[25]。 通过分析断口上的第二相成份, 2024铝合金中结晶相的主要成分是Al20Cu2(Fe, Mn)3, Mg2Si和Al2Cu[26], 因此尽量减少Fe、 Si元素的含量, 提高铝基体的纯度, 减少结晶相的含量, 可以提高铝合金的断裂韧性。 King[22]研究了铝合金中含有不同结晶相的体积分数, 测量其相应的断裂韧性值。 Staley[25]通过在7050高强铝合金中减少Fe、 Si含量, 即减少结晶相的体积分数, 提高了断裂韧性。 陈康华和张国君等[23, 27]的实验研究表明: 通过采用强化固溶的热处理制度可以提高合金的断裂韧性。 因为经强化固溶处理的试样, 其可溶结晶相的固溶程度增强, 含量减少, 从而减少一级微裂纹的形成, 提高了铝合金的断裂韧性。 上述实验结果和模型的解析结果在变化趋势和数值上的基本吻合, 说明了该模型能较好地预测材料的断裂韧性。
2.2 二级微裂纹对材料断裂韧性的影响
图3所示为材料的相对断裂韧性与韧带区二级微裂纹体积分数的关系(以含一级微裂纹体积分数为0.9%的材料为参考态)。 从图中可以看出, 随着韧带区二级微裂纹体积分数的增加, 材料的断裂韧性也随着下降, 特别是当韧带区一旦萌生二级微裂纹, 材料的断裂韧性陡降, 而后趋于平缓。 实际上, 在一级微裂纹之间萌生一个二级微裂纹, 使空洞之间的韧带区长度减半, 使得韧带区的应变增加, 一级微裂纹之间更容易连通, 从而显著降低了断裂韧性。 对7075铝合金的断裂韧性研究结果也表明了这个变化规律[28]。
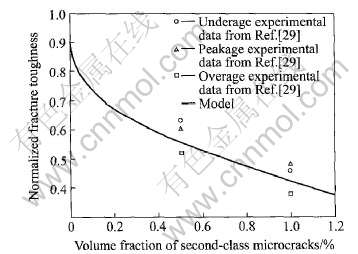
图3 二级微裂纹对材料断裂韧性的影响
Fig.3 Effect of second-class microcracks on fracture toughness
高强铝合金未溶结晶相优先断裂, 成为一级微裂纹, 随着应变的增加, 弥散相和粗大的析出相界面脱粘或断裂, 成为二级微裂纹。 Argon 等[28] 已经报道了铝合金中含有极少的结晶相时, 弥散相成为二级微裂纹形核的区域。 在铝合金中分别添加Mn、 Cr、 Zr, 形成较大的含Mn的弥散相、 较小的含Cr的弥散相和更小的含Zr的弥散相。 通过降低铝合金中弥散相的尺寸, 其断裂韧性依次提高。 Walsh等[28]在铝合金中添加少量微量元素, 在晶内形成非剪切的细小弥散相, 使晶内滑移均匀化, 不在晶界上造成应变集中, 尽量减少了晶界的开裂, 即减少了作为二级微裂纹的晶界开裂的几率, 提高了其断裂韧性。 Dumont等[29] 将固溶处理后含有未溶结晶相(Al2CuFe, Al2CuMg和Mg2Si, 体积分数约为0.9%)的7075铝合金试样, 分别采用3种不同的冷却速率进行淬火: 1)冷水冷却(快速冷却速率F=850K/s); 2) 温水冷却(中速冷却速率I=19K/s); 3) 沸水冷却(慢速冷却速率S=7K/s)。 较慢速率的淬火在合金中形成了数量较多的粗大析出相。 通过TEM和SEM观察和测量, 在快速冷却条件下, 合金中没有粗大的析出相的析出; 在中等冷却条件下, 析出相平均直径约为200nm, 其体积分数约为0.5%; 在慢速冷却条件下, 从合金中能析出更多粗大相, 其平均直径约为200nm, 体积分数约为1%。 最后将试样分别进行时效处理: 1) 欠时效(UA); 2) 峰时效(PA); 3) 过时效(OA)。 通过实验验证, 这些粗大的析出相能使晶界脆化, 萌生二级微裂纹, 且其体积分数越大, 7075铝合金的断裂韧性越差。 图3中实验数据点为AA7075铝合金在不同时效状态下, 采用不同的淬火速率, 其断裂韧性的相对变化值。 上述实验结果与其模型的解析值的吻合较好, 表明了本模型的有效性。
2.3 双级微裂纹对材料断裂韧性的影响
在高强铝合金中, 存在三类相。 结晶相无强化作用, 但成为一级微裂纹, 对韧性的危害最大。 弥散相的作用是阻碍再结晶和晶粒长大, 提高强度, 减少晶界裂纹, 提高韧性; 但较大的弥散相也会萌生二级微裂纹, 影响铝合金的韧性。 另外, 过时效或者慢速淬火形成的较大尺寸的析出相也会诱发二级微裂纹, 影响合金的断裂韧性。 三类相导致的双级微裂纹对韧性的影响可用本模型进行定量分析。
图4(a)所示为取含0.01%一级微裂纹体积分数的材料为参考态, 得到材料的相对断裂韧性。 比较了3种不同情况下材料的相对断裂韧性: 1) 材料内部只有一级微裂纹, 不存在二级微裂纹(m=0, a=10μm); 2) 材料内部有一级微裂纹, 且韧带区存在一个二级微裂纹(m=1, a=10μm, b=0.5μm); 3) 材料内部有一级微裂纹, 且韧带区存在2个二级微裂纹(m=2, a=10μm , b=0.5μm)。 从图中可以看出, 随着一级微裂纹体积分数的增加, 材料的断裂韧性开始迅速下降, 而后缓慢降低。 当一级微裂纹体积分数一定时, 材料的断裂韧性随韧带区二级微裂纹数目的增加而减小, 且二级微裂纹数目越多, 其断裂韧性降低得越快。 这是由于二级微裂纹数目的增加, 降低了韧带区的尺寸以及不同级微裂纹应变场的叠加所造成的。
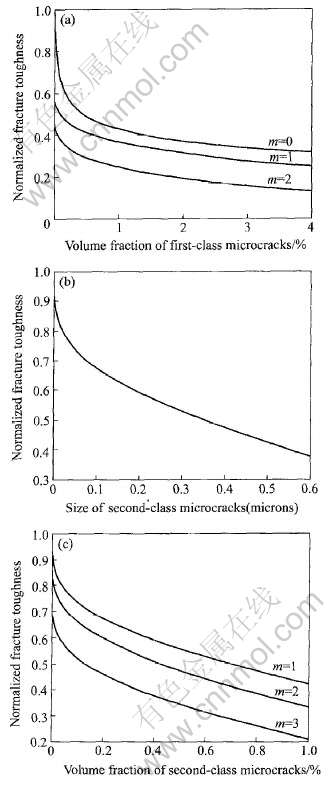
图4 两种尺度微裂纹对断裂韧性的影响
Fig.4 Effects of first-scale and second- scale microcracks on fracture toughness
图4(b)所示为取含1%一级微裂纹体积分数的材料为参考态, 得到材料的相对断裂韧性。 从图中可以看出, 材料的断裂韧性随着二级微裂纹长度的增加而下降。 众所周知, 裂纹尖端附近的应变随着裂纹尺度的增加而升高, 因此, 二级微裂纹长度的增加, 加剧了应变的集中而降低了材料的断裂韧性。
图4(c)所示为取含1%一级微裂纹体积分数的材料为参考态, 得到材料的相对断裂韧性。 从图中可以看出, 材料的断裂韧性随着二级微裂纹体积分数的增加而降低。 当二级微裂纹体积分数一定时, 二级微裂纹的数目越多, 其长度越小, 韧带区的尺寸也越小。 实际上, 在相同的二级微裂纹体积分数下, 韧带区的尺寸与二级微裂纹的长度呈线性关系。 因此可以看出: 韧带区二级微裂纹数目对材料断裂韧性的影响比其尺寸要大。
3 结论
1) 建立了高强金属材料断裂韧性与多相组织关系的解析模型, 可预测第二相转化的双级微裂纹对材料断裂韧性的影响。
2) 模型预测和实验均表明, 随着一级微裂纹体积分数的增加, 材料的断裂韧性开始迅速下降, 而后缓慢降低; 材料的断裂韧性随二级微裂纹的萌生而显著减小, 且二级微裂纹数目对材料断裂韧性的影响比其尺寸的影响显著。
3) 对于高强铝合金, 可以通过提高铝基体纯度或强化结晶相固溶, 减少结晶相的数量, 从而减少一级微裂纹的形成; 避免粗大弥散相和析出相的形成、 减少晶界的开裂, 尽量减少二次微裂纹的形成, 可以提高铝合金的断裂韧性。
REFERENCES
[1]Argon A S, Im J, Safoglu R. Cavity formation from inclusions in ductile fracture[J]. Metall Trans A, 1975, A6: 825-837.
[2]潘志军, 黎文献. 高强铝合金断裂韧性的研究现状及展望[J]. 材料导报, 2002, 16(7): 14-17.
PAN Zhi-jun, LI Wen-xian. Current status and future trends of research on fracture toughness of high strength aluminum alloys[J]. Material Review, 2002, 16(7): 14-17.
[3]贺永东, 张新明, 游江海, 等. 淬火无析出区对Al-Zn-Mg-Cu合金断裂行为的影响[J]. 中国有色金属学报, 2006, 16(3): 392-399.
HE Yong-dong, ZHANG Xin-ming, YOU Jiang-hai, et al. Effect of precipitate free zone quench-induced on fracture behavior of Al-Zn-Mg-Cu alloys[J]. The Chinese Journal of Nonferrous Metals, 2006, 16(3): 392-399.
[4]Vijaya S, Syatyaprasad K, Gokhale A. Effect of minor Sc additions on structure, age hardening and tensile properties of Al alloy AA8090 plate[J]. Scripta Mater, 2004, 50: 903-908.
[5]Phillips M A, Clemens B M, Nix W D. A model for dislocation behavior during deformation of Al/Al3Sc(fcc/LI2)multilayers[J]. Acta Mater, 2003, 51: 3157-3170.
[6]Sun J. Stress triaxiality constraint and crack tip parameters[J]. Engineering Fracture Mechanics, 1993, 44: 789-806.
[7]Ashby M F. The deformation of plastically non-homogeneous materials[J]. The Philosophical Magazine, 1970, 21: 399-424.
[8]Poech M H, Fisch meister H F. Contribution of void growth to the crack resistance of ductile materials[J]. Engineering Fracture Mechanics, 1992, 43: 581-588.
[9]Chan K S. A fracture model for hydride-induced embrittlement[J]. Acta Metallurgica Materialia, 1995, 43: 4325-4335.
[10]刘刚, 张国君, 孙军, 等. 含有不同尺度量级第二相的高强铝合金断裂韧性模型[J]. 中国有色金属学报, 2002, 12(4): 706-713.
LIU Gang, ZHANG Guo-jun, SUN Jun, et al. A model for fracture toughness of high strength aluminum alloys containing second particles of various sized scales[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(4): 706-714.
[11]Underwood E E. Quantitative Stereology[M]. MA: Addison-Wesley, 1970. 237.
[12]Thomason P F. Ductile Fracture of Metal[M]. Oxford: Pergamon Press, 1990: 534-548.
[13]Hutchinson J W. Sigular behavior at the end of a tensile crack in a hardening material[J]. J Mech Phys Solids, 1968, 16: 13-16.
[14]Rice J R, Rosengrn G F. Plane deformation near a crack tip in a power-law hardening material[J]. J Mech Phys Solids, 1968, 16: 1-12.
[15]Edwards L, Martin J W. Strength of Metals and Alloys[M]. Oxford: Pergamon Press, 1982: 22-30.
[16]Hutchinson J W. Singular behavior at the end of a tensile crack in a hardening material[J]. Journal of Mechanisms in Physics and Solids, 1968, 16: 13-31.
[17]Rice J R, Rosengren G F. Plane strain deformation near a crack tip in a power-law hardening material[J]. Journal of Mechanisms in Physics and Solids, 1968, 16: 1-12.
[18]Shih C F. Plastic deformation in metals[J]. Astmstp, 1974, 560: 187-218.
[19]McClintock F A. Fundamental Aspects of Structural Alloy Design[M]. New York: Wilcox, Plenum, 1977: 147.
[20]Dowling N E. J-integral estimates for cracks in infinite bodies[J]. Engineering Fracture Mechanics, 1987, 26: 333-348.
[21]Garrett G G, Knott J F. Influence of compositional and microstructural variation on mechanism of static fracture in aluminum alloys[J]. Metallurgical Transaction A, 1978, 9A: 1187-1201.
[22]King F. Aluminum and Its Alloys[M]. Chichester: Ellis Horwood Limited, 1987: 27-42.
[23]张国君, 刘刚, 孙军, 等. 含有不同尺度量级第二相的高强铝合金拉伸延性模型[J]. 中国有色金属学报, 2002, 12(S1): 1-10.
ZHANG Guo-jun, LIU Gang, SUN Jun, CHEN Kang-hua. A model for tensile ductility of high strength aluminum alloys containing second particles of various sized scales[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(S1): 1-10.
[24]Hornbogen E A, Starke J R. Theory assisted design of high strength low alloy aluminum[J]. Acta Metallurgica Materialia, 1993, 41: 1-16.
[25]Staley J T. In properties related to fracture toughness[J]. Astm Stp, 1975, 605: 71-103.
[26]Walsh J A. The influence of Mn dispersoid content and stress state on ductile fracture of 2134 type Al alloys[J]. Acta Metall, 1989, 37: 2861-2871.
[27]CHEN Kang-hua, LIU Hong-wei, ZHANG Zhuo, et al. The improvement of constituent dissolution and mechanical properties of 7055 aluminum alloy by stepped heat treatments[J]. J Mater Proc Technol, 2003, 142: 190-196.
[28]van Stone R H, Merchant R H, Low Jr J R. In Fatigue and Fracture Toughness-cryogenic Behavior[M]. Oxford: Pergamon Press, 1973: 556-568.
[29]Dumont D, Deschamps A, Brechet Y. On the relationship between microstructure, strength and toughness in AA7050 aluminum alloy[J]. Mater Sci Eng A, 2003, A356: 326-336.
(编辑陈爱华)
基金项目: 国家重点基础研究发展规划资助项目(2005CB623704); 国家自然科学基金资助项目(50471057); 教育部新世纪优秀人才支持计划资助项目(NCET-04-0752)
收稿日期: 2006-01-16; 修订日期: 2006-06-15
通讯作者: 陈康华, 教授; 电话: 0731-8830714; E-mail: khchen@mail.csu.edu.cn