扶手椅型石墨烯纳米带(AGNRs)电子结构的应力调控
黄丽,蒋练军,熊翠秀,张光富
(湖南城市学院 通信与电子工程学院,湖南 益阳,413000)
摘要:当单轴拉伸应变沿扶手椅型石墨烯纳米带的扶手椅边沿时,利用静力学方法建立石墨烯纳米带的键角、键长与应力的解析关系;利用紧束缚方法对扶手椅边石墨烯纳米带的能带与能隙及应力的关系进行解析计算。研究结果表明:微小应变会导致纳米条带的能带宽度发生变化,并打开金属型扶手椅石墨烯纳米带能隙,费米能级附近的半导体型扶手椅石墨烯纳米带的能隙宽度也相应地发生改变;能隙随应变呈线性的周期变化,并且表现出明显的震荡现象;可达到的最大能隙随应力增大有所增大,随条带横向原子数m增大而减小。
关键词:紧束缚方法;单轴应力;能带;能隙
中图分类号:TB33;O469 文献标志码:A 文章编号:1672-7207(2013)03-1063-07
Electronic structure engineering of AGNRs by uniaxial strain
HUANG Li, JIANG Lianjun, XIONG Cuixiu, ZHANG Guangfu
(Department of Physics & Electronic-Information Engineering, Hunan City University, Yiyang 413000, China)
Abstract: The analytic relationship among armchair graphene nanoribbons’ bond angles and bond lengths and the uniaxial tensile strain along armchair edge was established by the static method. By the tight binding method, the relationship among armchair graphene nanoribbons’s energy band and band gap and strain was calculated. The results show that the application of a small uniaxial strain leads to variation of energy subband spacing, which opens a band gap for metallic AGNRs and modifies the band gaps for semiconducting AGNRs near the Fermi level. Energy gap displays linear periodic variation with the strain, and shows obvious shock phenomenon. The maximum energy gap increases when the stain increases, and the maximum energy gap decreases when the strip transverse atomic number increases.
Key words: tight binding method; uniaxial strain; energy gap; energy band gap
石墨烯纳米条带(GNRs)是石墨烯的基本结构单元。近年来,GNRs作为一种新颖的碳基纳米材料引起了人们的广泛关注[1-5]。不同宽度的石墨烯纳米带可通过多种常规方法制备[2-3],有望对未来的纳米电子学产生重要影响,其电子结构的基础理论研究也将为实验与应用研究提供强有力的依据。采用力学方法可调控GNRs的电子能带结构与物性,可成为一种GNRs能带调控的新途径。很多研究者利用第一性原理[6-7]、紧束缚方法[8-10]、非平衡格林函数方法和密度范函理论[10]等从理论上探讨了力学应变对石墨烯系统电子结构及光学性质的影响,为石墨烯纳米带应力调控的研究打下了良好的基础。在较小的力作用下,石墨烯中碳原子键长变化较小,体系费米能级附近的状态仍然主要由2pz轨道来决定,边缘吸附外来原子和存在的空位与替位原子时的情况也一样,因此,仍然可以采用紧束缚近似方法计算和研究其能带结构。本文在以上研究成果的基础上,考虑微小平面单轴应变力沿理想、完整的扶手椅型石墨烯纳米带的扶手椅边沿时,在不计纳米带长收缩且只考虑最邻近相互作用的情况下,利用静力学方法,建立石墨烯纳米带的键角、键长与拉力的解析关系;然后,利用紧束缚方法对扶手椅边石墨烯纳米带的能带与拉力的关系进行解析计算,得到单轴应力对扶手椅型石墨烯纳米带的能带及带隙的调控规律,以便为石墨烯纳米条带在能隙工程及应力传感器方面的应用提供依据。
1 分析模型
建立如图1所示模型。沿扶手椅型石墨烯纳米带(AGNR)的扶手椅边沿施加一微小单轴应力f,f与石墨烯纳米条带处于同一平面且拉伸时非常缓慢,可以看作一静力。假设模型中石墨烯纳米带的带宽W足够宽,以致可以将石墨烯纳米带看作是1个石墨烯面,并且石墨烯纳米带的长度L相对宽度W来说无限长,即L>> W。由于应力在拉伸时非常缓慢且石墨烯纳米带L>> W,所以,可以忽略石墨烯纳米带带长的收缩。
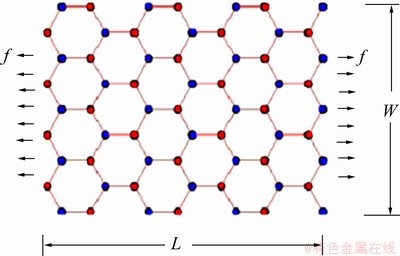
图1 单轴应力沿扶手椅型石墨烯纳米带扶手椅边沿示意图
Fig.1 Sketch for ANGR with uniaxial strain distributed along armchair direction
2 方法与讨论
扶手椅型石墨烯纳米带受到沿扶手椅边沿的单轴应力拉伸时,在只考虑最邻近相互作用的情况下,利用静力学方法,对任意1个碳原子进行受力分析,如图2所示,其中:f为拉力分配到每个碳原子上的力;△f1和△f2为相邻碳原子因键长发生变化而产生的力; 为半键角;△R1,△R2和△R3为相邻碳原子键长的变化量;
为半键角;△R1,△R2和△R3为相邻碳原子键长的变化量;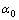 和
和 分别为不受外力及受到拉伸应力时相邻碳原子的半键角;R1,R2和R3为受到拉伸应力时相邻碳原子的键长。可得到半键角及相邻碳原子键长变化与拉力的解析关系式为[9]
分别为不受外力及受到拉伸应力时相邻碳原子的半键角;R1,R2和R3为受到拉伸应力时相邻碳原子的键长。可得到半键角及相邻碳原子键长变化与拉力的解析关系式为[9]
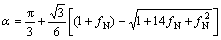 (1)
(1)
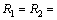
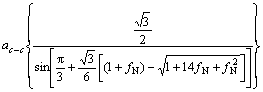 (2)
(2)
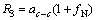 (3)
(3)
其中:相邻碳原子不受应力时的键长ac-c=1.42×10-10 m;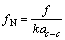 ,为无量纲量;k为弹性系数。
,为无量纲量;k为弹性系数。
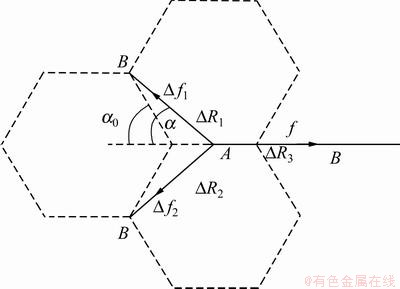
图2 应力沿扶手椅型石墨烯纳米带扶手椅边沿时任一碳原子的受力分析图
Fig.2 Force analysis map of a carbon atom of AGNR with uniaxial strain distributed along armchair direction
对半键角 、键长R与fN进行解析计算,得到
、键长R与fN进行解析计算,得到 与fN关系及R与fN的关系,分别如图3和图4所示。
与fN关系及R与fN的关系,分别如图3和图4所示。
由图3和图4可见:当拉伸应力沿扶手椅边沿拉伸石墨烯带时,其半键角 随应力增大变化明显,键长R1(R1=R2)和R3随应力增大显著增加,并都呈线性变化规律,但R3的变化比R1(R1=R2)稍快,这与文献[9, 17]中给出的结论一致;拉伸应力作用引起石墨烯纳米带键长发生变化,这会引起最邻近碳原子跳跃能发生相应改变[5],而跳跃能决定能带,因此,可以通过外加应力来调控石墨烯纳米带的能带和能隙。
随应力增大变化明显,键长R1(R1=R2)和R3随应力增大显著增加,并都呈线性变化规律,但R3的变化比R1(R1=R2)稍快,这与文献[9, 17]中给出的结论一致;拉伸应力作用引起石墨烯纳米带键长发生变化,这会引起最邻近碳原子跳跃能发生相应改变[5],而跳跃能决定能带,因此,可以通过外加应力来调控石墨烯纳米带的能带和能隙。
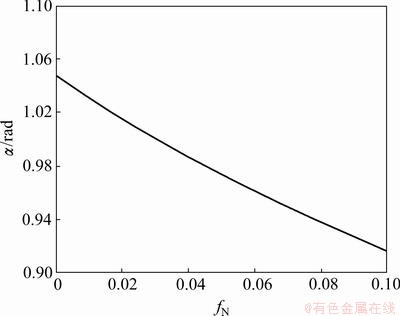
图3 单轴应力作用下半键角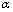 与无量纲量fN的关系
与无量纲量fN的关系
Fig.3 Relationship between half-bond angle 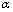 and dimensionless physical quantity fN under uniaxial strain
and dimensionless physical quantity fN under uniaxial strain
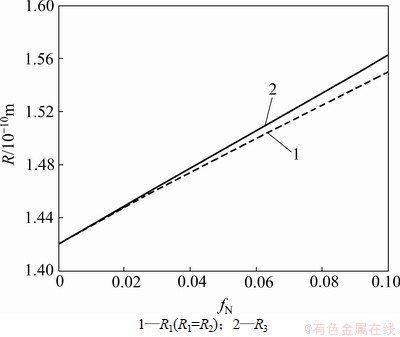
图4 单轴应力作用下键长R与无量纲量fN的关系
Fig.4 Relationship between bond-lengths R and dimensionless physical quantity fN under uniaxial strain
图5所示为沿扶手椅边沿方向的单轴应力作用下石墨烯纳米带元胞模型,其中:lx和ly表示均匀应变下扶手椅型石墨烯纳米带的平行四边形元胞的2条对角线长度;黑、灰两色的小球A和B代表子格点。在外加微小的单轴应力作用下,体系费米能级附近的电子态仍然主要由形成σ键的2pz轨道决定,并且石墨烯纳米带的电子结构可以用紧束缚近似下的π轨道来描述。因为在均匀单轴应变下,理想完整宽度为m-AGNRs的晶格周期性仍然保持与非应力作用下的情形一致。
根据紧束缚近似方法,在只考虑最邻近相互作用时,在应变作用下,扶手椅型石墨烯纳米带的能带可表示为[6, 10]
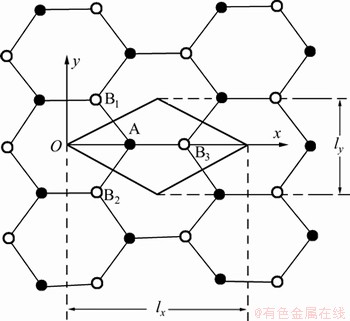
图5 单轴应变沿扶手椅型石墨烯纳米带的扶手椅边沿时的元胞示意图
Fig.5 Graph of unit cell of AGNR with uniaxial strain distributed along armchair direction
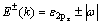 (4)
(4)
其中: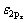 为原子位能,对于理想结构的石墨烯,通常取0。在应力作用下,扶手椅型石墨烯纳米带的能带可用下式表示:
为原子位能,对于理想结构的石墨烯,通常取0。在应力作用下,扶手椅型石墨烯纳米带的能带可用下式表示:
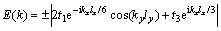 (5)
(5)
其中:“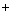 ”和“
”和“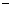 ”分别表示导带和价带的表达式;在横向硬壁势限制条件下,旁带波矢
”分别表示导带和价带的表达式;在横向硬壁势限制条件下,旁带波矢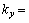
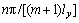 ;旁带指标n=1, 2, …, m,为扶手椅型石墨烯纳米带横向原子数,直接反映条带宽度m的大小;纵向波矢kx在第一布里渊区内可连续取值;t1(t1=t2)和t3为碳原子在最近临的晶格位置之间的跃迁能,
;旁带指标n=1, 2, …, m,为扶手椅型石墨烯纳米带横向原子数,直接反映条带宽度m的大小;纵向波矢kx在第一布里渊区内可连续取值;t1(t1=t2)和t3为碳原子在最近临的晶格位置之间的跃迁能,
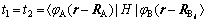
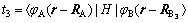 (6)
(6)
RA为碳原子A的位置矢量;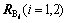 ,
,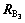 为与碳原子A最临近的3个碳原子B与碳原子A的相对位量矢量(见图6);H为系统的哈密尔顿函数;
为与碳原子A最临近的3个碳原子B与碳原子A的相对位量矢量(见图6);H为系统的哈密尔顿函数;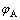 和
和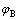 分别表示碳原子A和B晶格位置的轨道波函数。在应力作用下,最邻近的两碳原子间的跳跃能ti取决于键长的改变量,它与键长的关系满足哈里森公式[11-12]:
分别表示碳原子A和B晶格位置的轨道波函数。在应力作用下,最邻近的两碳原子间的跳跃能ti取决于键长的改变量,它与键长的关系满足哈里森公式[11-12]:
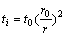 (7)
(7)
式中:t0为不受应力时最邻近的2个碳原子间的跳跃能,t0=-2.70 eV;r0和r分别表示不受应力与受到应力时的键长。图7所示的碳原子A与最邻近的3个碳原子B的键长变化,可表示为[11-12]:
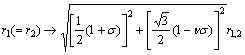
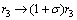 (8)
(8)
式中: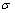 为沿扶手椅边沿的应变;
为沿扶手椅边沿的应变;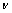 为泊松比[17],
为泊松比[17],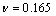 。
。
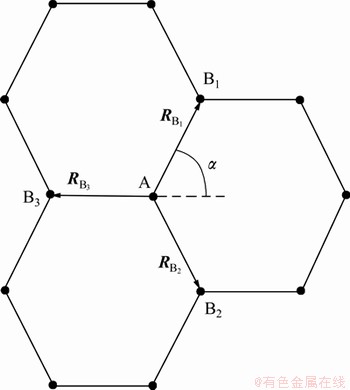
图6 最临近碳原子A和B的相对位置矢量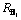 ,
,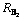 ,
,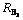 以及半健角
以及半健角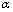 的标识图
的标识图
Fig.6 Sketch map of relative position site vectors 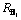 ,
,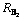 ,
,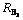 of nearest neighbor carbon atoms A and B and half-bond angle
of nearest neighbor carbon atoms A and B and half-bond angle 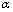
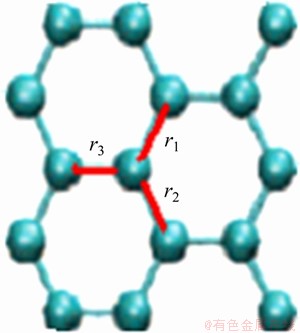
图7 最邻近碳原子的键长示意图
Fig.7 Adjacent of nearest neighbor carbon atoms bond length
下面采用文献[10]中的方法对沿高对称性点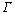 (费米点)到M的电子能带
(费米点)到M的电子能带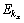 (以eV为单位)随布洛赫波kx的变化进行解析计算。当不受应力时,
(以eV为单位)随布洛赫波kx的变化进行解析计算。当不受应力时,
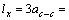 4.260×10-10 m;
4.260×10-10 m;
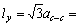 2.470×10-10 m
2.470×10-10 m
当受到沿扶手椅方向的应力时,
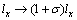 ;
; 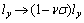
取应变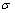 =8%,泊松比
=8%,泊松比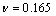 ,则受到应力时,
,则受到应力时,
lx=4.600×10-10 m; ly=2.437×10-10 m
由式(7)和(8)可求得不受应力时,
t1= t3= t0=-2.70 eV
当应变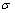 =8%时,
=8%时,
t1=-2.64 eV, t3=-2.31 eV
石墨烯纳米带在第一布里渊区的高对称点如图8所示,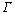 和M的坐标为
和M的坐标为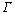 =(0, 0),
=(0, 0),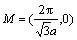 (其中,a为晶格常数,a=2.46×10-10 m)。
(其中,a为晶格常数,a=2.46×10-10 m)。
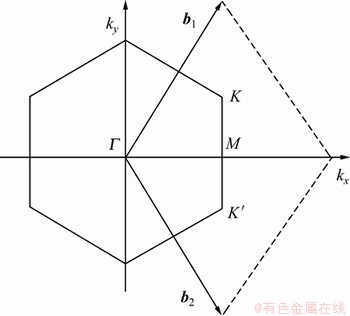
图8 石墨烯的第一布里渊区中倒格子矢和高对称点图
Fig.8 Graph of the first Brillouin zone, reciprocal lattice vectors and high symmetry points
沿着高对称性点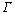 到M的电子能带
到M的电子能带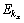 (以eV为单位)随布洛赫波矢kx变化的解析计算结果如图9所示。由图9可知:在理想的非应变情形下,曲6-扶手椅型石墨烯纳米带、7-扶手椅型石墨烯纳米带和8-扶手椅型石墨烯纳米带大多呈现抛物线形状变化的子带,但7-扶手椅纳米带n=4的子带是平坦的。具体标记和识别石墨烯纳米带的子带将有益于选择光学跃迁和输运性质[13]。对于半导体型6-扶手椅石墨烯纳米带(如图9(a)实线所示),在
(以eV为单位)随布洛赫波矢kx变化的解析计算结果如图9所示。由图9可知:在理想的非应变情形下,曲6-扶手椅型石墨烯纳米带、7-扶手椅型石墨烯纳米带和8-扶手椅型石墨烯纳米带大多呈现抛物线形状变化的子带,但7-扶手椅纳米带n=4的子带是平坦的。具体标记和识别石墨烯纳米带的子带将有益于选择光学跃迁和输运性质[13]。对于半导体型6-扶手椅石墨烯纳米带(如图9(a)实线所示),在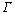 点的导带序列自上而下分别为1,2,3,6,4和5,因价带和导带关于费米能
点的导带序列自上而下分别为1,2,3,6,4和5,因价带和导带关于费米能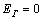 对称分布,所以,约有1.34 eV的带隙;如图9(b)实线所示,半导体型7-扶手椅石墨烯纳米带的导带序列为1,2,3,4,7,6和5,带隙为1.28 eV;如图9(c)实线所示,金属型的8-扶手椅石墨烯纳米带的导带序列为l,2,3,4,8,5,7和6,没有能隙。
对称分布,所以,约有1.34 eV的带隙;如图9(b)实线所示,半导体型7-扶手椅石墨烯纳米带的导带序列为1,2,3,4,7,6和5,带隙为1.28 eV;如图9(c)实线所示,金属型的8-扶手椅石墨烯纳米带的导带序列为l,2,3,4,8,5,7和6,没有能隙。
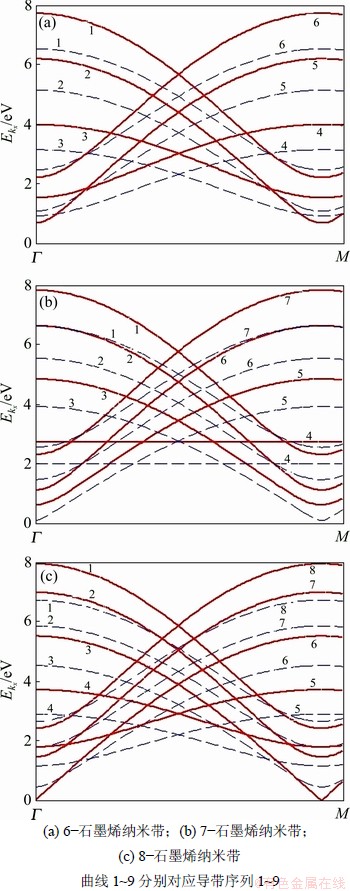
图9 单轴应变沿扶手椅型石墨烯纳米带的扶手椅边沿时导带的能带结构,其中实线和虚线分别对应理想(非外加应变)和应变情形下导带的子带
Fig.9 (Color online) Energy bands of m-AGNRs with uniaxial strain distributed along armchair direction, where (red) solid and (blue) dashed lines for unstrained and strained case in which red and blue numbers denote the order number of CB subbands for the unstrained and strained case, respectively
在外加应变情形下(如图9中虚线所示),扶手椅型石墨烯纳米带的能带与理想情形不再相同;当应变沿扶手椅边沿时(如图9(a)中虚线所示),6-扶手椅石墨烯纳米带在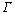 点的导带序列自上而下从理想的导带序列l,2,3,6,4和5变为1,2,3,6,5和4,其中,子带3和4与理想情形平行,而其余子带比理想情形平坦,条带能隙也拓宽到1.84 eV。可见:应变除了改变子带序列外,还有效调节了半导体型6-扶手椅石墨烯纳米带的带隙。在应力作用下,将半导体型7-扶手椅石墨烯纳米带的情形与6-扶手椅石墨烯纳米带比较,尽管二者均具有半导体特征,但能带情况却有所不同。半导体型7-扶手椅石墨烯纳米带的情形如图9(b)中虚线所示,在
点的导带序列自上而下从理想的导带序列l,2,3,6,4和5变为1,2,3,6,5和4,其中,子带3和4与理想情形平行,而其余子带比理想情形平坦,条带能隙也拓宽到1.84 eV。可见:应变除了改变子带序列外,还有效调节了半导体型6-扶手椅石墨烯纳米带的带隙。在应力作用下,将半导体型7-扶手椅石墨烯纳米带的情形与6-扶手椅石墨烯纳米带比较,尽管二者均具有半导体特征,但能带情况却有所不同。半导体型7-扶手椅石墨烯纳米带的情形如图9(b)中虚线所示,在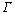 点的导带序列自上而下从理想的l,2,3,4,7,6和5变为1,2,3,7,4,6和5;第3,4,5子带与理想情况平行,其余子带比理想情形平坦,在
点的导带序列自上而下从理想的l,2,3,4,7,6和5变为1,2,3,7,4,6和5;第3,4,5子带与理想情况平行,其余子带比理想情形平坦,在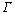 点的带隙只有不受应力情形下的1/4;此外,由局域在7-扶手椅石墨烯纳米带奇数排原子的2pz轨道形成的第4导带子带(完全平坦,与波矢kx无关)从非应变的2.70 eV变化到2.03 eV。如图9(c)中虚线所示,金属型8-扶手椅石墨烯纳米带在
点的带隙只有不受应力情形下的1/4;此外,由局域在7-扶手椅石墨烯纳米带奇数排原子的2pz轨道形成的第4导带子带(完全平坦,与波矢kx无关)从非应变的2.70 eV变化到2.03 eV。如图9(c)中虚线所示,金属型8-扶手椅石墨烯纳米带在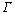 点的导带序列自上而下从理想的1,2,3,4,8,5,7和6变为1,2,3,4,8,7,5和6,其中,第4和第5子带与理想情形平行,其余子带比理想情形平坦,子带6的线性部分消失,产生了0.92 eV的能隙。
点的导带序列自上而下从理想的1,2,3,4,8,5,7和6变为1,2,3,4,8,7,5和6,其中,第4和第5子带与理想情形平行,其余子带比理想情形平坦,子带6的线性部分消失,产生了0.92 eV的能隙。
下面探讨扶手椅石墨烯纳米带能隙与单轴应力的关系。扶手椅石墨烯纳米带的能隙Eg可以通过下式计算:
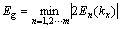 (9)
(9)
其中: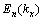 为扶手椅石墨烯纳米带在
为扶手椅石墨烯纳米带在 时的本征能量谱;n为子带数;m为横向原子数,直接反映了条带宽度。在单轴应力作用下,不计带长收缩且只考虑最邻近相互作用时,将扶手椅石墨烯纳米带在费米点(
时的本征能量谱;n为子带数;m为横向原子数,直接反映了条带宽度。在单轴应力作用下,不计带长收缩且只考虑最邻近相互作用时,将扶手椅石墨烯纳米带在费米点( )的本征能量谱
)的本征能量谱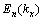 计算公式近似表示为[11-14]
计算公式近似表示为[11-14]
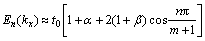 (10)
(10)
其中:t0为不受应力时最邻近碳原子之间的跃迁能,一般取-2.70 eV,而
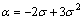
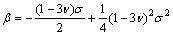
泊松比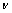 取0.165。取应力的一阶近似,得到应力作用下扶手椅石墨烯纳米带的能隙为
取0.165。取应力的一阶近似,得到应力作用下扶手椅石墨烯纳米带的能隙为
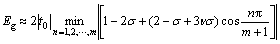 (11)
(11)
在沿扶手椅边沿方向的单轴应力作用下,扶手椅石墨烯纳米带的能隙与应变的关系图线及在一定应力下能隙与横向原子数m的关系分别如图10和图11所示。
由图10可知:在沿扶手椅边沿的单轴应力作用下,扶手椅石墨烯纳米带的能隙随应变呈线性的周期性变化,并且表现出明显的震荡现象;可达到的最大能隙随应力增大有所增大,且最大能隙随条带横向原子数(条带宽度)m增大而减小。由图11可知:应变下扶手椅石墨烯纳米带的能隙总的变化趋势是随着m的增大而减小,在m较小的区域急剧振荡变化,如图11中曲线1所示;在非应变下,理想的扶手椅石墨烯纳米带能隙随横向原子数m以3为周期发生金属—半导体转变,并振荡下降;如图11中曲线2所示。由于应变下纳米带结构对称性降低,扶手椅石墨烯纳米带不再有上述周期性的变化规律,这与文献[10]中的研究结果一致。可见:扶手椅石墨烯纳米带的能隙可以通过外加应变进行有效调控,并有望应用于应力传感器等方面的设计[15-19]。
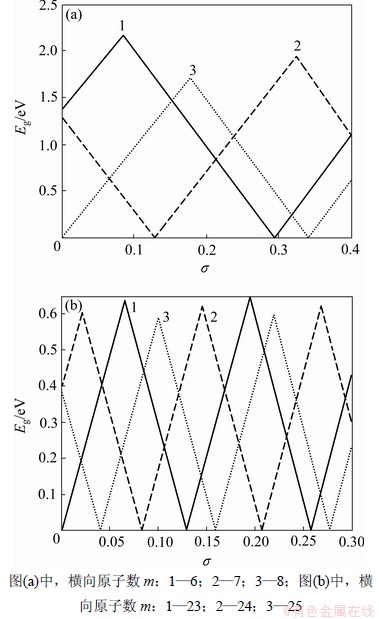
图10 沿扶手椅边沿的单轴应力作用下不同宽度扶手椅型石墨烯纳米带的能隙与应变关系
Fig.10 Relationship between band gap and uniaxial strain along armchair direction for m-AGNRs

图11 沿扶手椅边沿的单轴应力作用下扶手椅型石墨烯纳米带的能隙与横向原子数m的关系
Fig.11 Relationship between band gap and number of atomic chains m under uniaxial strain along armchair direction for m-AGNRs
3 结论
(1) 应力沿扶手椅边沿拉伸扶手椅边的石墨烯纳米带时,条带的半键角 和键长随拉力增大变化明显,键长R1(R1=R2)和R3都随拉力增大呈线性增大;微小应变会导致纳米条带的能带宽度发生变化,并会打开金属型扶手椅石墨烯纳米带的带隙,从而使费米能级附近半导体型扶手椅石墨烯纳米带的带隙宽度发生改变。因此,通过改变应力的大小、作用方向及应力类型,可以实现对扶手椅石墨烯纳米带带隙的有效调控。
和键长随拉力增大变化明显,键长R1(R1=R2)和R3都随拉力增大呈线性增大;微小应变会导致纳米条带的能带宽度发生变化,并会打开金属型扶手椅石墨烯纳米带的带隙,从而使费米能级附近半导体型扶手椅石墨烯纳米带的带隙宽度发生改变。因此,通过改变应力的大小、作用方向及应力类型,可以实现对扶手椅石墨烯纳米带带隙的有效调控。
(2) 在沿扶手椅边沿的单轴应力作用下,扶手椅石墨烯纳米带的能隙随应变呈线性的周期变化,并且表现出明显的震荡现象;可达到的最大能隙随应力增大有所增大,且最大能隙随条带横向原子数m(条带宽度)增大而减小。
参考文献:
[1] ZHANG Yuanbo, TAN Yanwen, Stormer H L, et al. Experimental observation of the quantum hall effect and Berry’s phase in graphene[J]. Nature, 2005, 438(7065): 201-204.
[2] Son Y W, Cohen M L, Louie S G. Half-Metallic graphene nanoribbons[J]. Nature, 2006, 444(7117): 347-349.
[3] Berger C, SONG Zhimin, LI Xuebin, et al. Electronic confinement and coherence in patterned epitaxial graphene[J]. Science, 2006, 312(5777): 1191-1196.
[4] YAN Qimin, HUANG Bing, YU Jie. Intrinsic current-voltage characteristics of graphene nanoribbon transistors and effect of edge doping[J]. Nano Lett, 2007, 7(6): 1469-1473.
[5] KANG Jiahao, HE Yu, ZHANG Jinyu, et al. Modeling and simulation of uniaxial strain effects in armchair graphene nanoribbon tunneling field effect transistors[J]. Appl Phys Lett, 2010, 96(25): 252105.
[6] GUI Gui, LI Jin, ZHONG Jianxin. Band structure engineering of graphene by strain: First-principles calculations[J]. Phys Rev B, 2008, 78(7): 075435-6.
[7] HAN Mei, ZHANG Yong, ZHENG Hongbo. Effect of uniaxial strain on band gap of armchair-edge graphene nanoribbons[J]. Chin Phys Lett, 2010, 27(3): 037302.
[8] Pereira V M, Castro N A H, Peres N M R. A tight-binding approach to uniaxial strain in grapheme[J]. Phys Rev B, 2009, 80(4): 045401-8.
[9] 韦勇, 童国平. 拉伸作用对单层石墨片电子能隙的影响[J]. 物理学报, 2009, 58(3): 1931-1935.
WEI Yong, TONG Guoping. Effect of the tensile force on the electronic energy gap of graphene sheets[J]. Acta Phys Sin, 2009, 58(3): 1931-1935.
[10] LIAO Wenhu, ZHOU Benhu, ZHOU Guang-hui. Electronic structures for armchair-edge graphene nanoribbons under a small uniaxial strain[J]. Eur Phys J B, 2010, 76(3): 463-467.
[11] LU Yang, GUO Jing. Band gap of strained graphene nanoribbons[J]. Nano Res, 2010, 3: 189-199.
[12] Blakslee O L, Proctor D G, Seldin E J, et al. Elastic constants of compression-annealed pyrolytic graphite[J]. J Appl Phys, 1970, 41(8): 3373-3382.
[13] LIAO Wenhu, ZHOU Guanghui, FU Xi. Optical properties for armchair-edge graphene nanoribbons[J]. J Appl Phys, 2008, 104(12): 126105.
[14] White C T, LI Junwen, Gunlycke D, et al. Hidden one-electron interactions in carbon nanotubes revealed in graphene nanostrips[J]. Nano Lett, 2007, 7(3): 825-830.
[15] SUN Lian, LI Qunxiang, REN Hao, et al. Strain effect on electronic structures of graphene nanoribbons: A first-principles study[J]. J Chem Phys, 2008, 129(7): 074704.
[16] Barone V, Hod O, Scuseria G E. Electronic structure and stability of semiconducting graphene nanoribbons[J]. Nano Lett, 2006, 6(12): 2748-2754.
[17] 袁健美, 毛宇亮. 氢化与非氢化石墨烯纳米条带的密度泛函研究[J]. 物理学报, 2011, 60(10): 103103.
YUAN Jianmei, MAO Yuliang. Density functional study on hydrogenation and non-hydrogenation graphene nanoribbon[J]. Acta Phys Sin, 2011, 60(10): 13103.
[18] FANG Hui, WANG Ruzhi, CHEN Siying, et al. Strain-induced negative differential resistance in armchair-edge graphene nanoribbons[J]. Appl Phys Lett, 2011, 98(8): 082108.
[19] 梅光全. 锯齿边缘石墨烯纳米带的电子输运性质[J]. 苏州大学学报: 自然科学版, 2012, 28(2): 48-53.
MEI Guangquan. Electronic transport in zigzag graphene nanoribbons[J]. Journal of SooChow University: Natural Science Edition, 2012, 28(2): 48-53.
(编辑 陈灿华)
收稿日期:2012-07-10;修回日期:2012-09-22
基金项目:湖南省自然科学基金资助项目(12JJ3011);湖南省教育厅科研项目(11C0254)
通信作者:蒋练军(1966-),湖南安化人,教授,从事纳米材料和电磁材料的研究;电话:0737-6355059;E-mail: jianglianjun888@163.com