
DOI: 10.11817/j.issn.1672-7207.2020.02.010
声弹性螺栓应力测量影响因素
韩玉强1,吴付岗1,李明海1,梅军2,王小龙1
(1. 中国工程物理研究院 总体工程研究所,四川 绵阳,621900;
2. 中国工程物理研究院 成都科学技术发展中心,四川 成都,610200)
摘要:为了分析声弹性法螺栓应力测量中的影响因素,从固体质点声弹性理论入手,在模型中加入质点受力形变因素,建立质点时差法应力测量模型;针对螺栓结构建立不同轴向预紧力下应力分布,获得超声传播路径上的应力分布表达式,建立不均匀应力下的螺栓声弹性测量模型;设计应力不均匀区占超声路径比例不同的实验,采用基于ZnO压电薄膜的方式激发超声,压电薄膜溅射于螺栓表面,避免使用超声耦合层引入的测量误差,得到应力不均匀区与测试误差的关系;进行螺栓反复拉伸后声弹性测量的重复性实验,验证材料性质与螺栓应力测量的关系。研究结果表明,超声时差与应力呈线性关系;声弹性系数由螺栓的弹性模量、泊松比以及螺栓长度决定;不同应力非均匀区占比的螺栓应力测量误差相同,初始误差小于2%;螺栓反复拉伸后,声弹性螺栓应力测量误差变大;应力分布不会产生测量误差,测量误差来源于材料的非均匀性;经过拉伸后的螺栓,材料中的缺陷和错位增大,增强高频超声的散射,引起应力测量误差变大。
关键词:声弹性;应力分布;压电薄膜;误差
中图分类号:TH73 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207(2020)02-0359-08
Factors influencing measurement of bolt stress based on acoustoelastic effect
HAN Yuqiang1, WU Fugang1, LI Minghai1, MEI Jun2, WANG Xiaolong1
(1. Institute of System Engineering, China Academy of Engineering Physics, Mianyang, 621900, China;
2. Chengdu Development Center of Science and Technology, China Academy of Engineering Physics,Chengdu, 610200, China)
Abstract: In order to analyze the influence of various factors on the measurement of bolt stress by acoustoelastic effect, the theory of acoustoelastic of solid particles was analyzed. The stress and deformation factors of particles were introduced into the model and the stress measurement model of particles was established. The stress distributions under different axial preloads was established with the structure of bolt, the stress distribution expression on the ultrasonic propagation path was obtained and the acoustoelastic measurement model of bolt under uneven stress was established. ZnO piezoelectric film, which was sputtered on the bolt surface, was used to generate ultrasonic and could avoid the measurement error caused by the application of the ultrasonic coupling layer. The relationship between the uneven stress area and the measurement error was obtained. The relationship between the properties of materials and the stress measurement of bolts was verified by the repeated experiments of acoustoelastic measurement after repeated stretching of bolts. The results show that the ultrasonic time difference is linear with the stress. The acoustoelastic coefficient is determined by the elastic modulus, Poisson's ratio and length of bolt. The error of the different ratios of uneven stress area is the same and the initial error is less than 2%. The error of measurement increases after the bolt is repeatedly stretched. The stress distribution can not produce measurement errors while measurement error comes from the non-uniformity of the material. After stretching the bolt, the defects and dislocation in the material increase which may enhance the scatter of high-frequence ultrasonic and amplify the error.
Key words: acoustoelastic; stress distribution; piezoelectric film; error
螺栓连接强度对系统的可靠性有重要意义。螺栓应力过小造成结构失效,而应力过大造成疲劳损伤进而影响结构稳定性,因此,对螺栓应力进行快速、无损、在线测试具有应用价值。在多种螺栓应力测试方法中,声弹性法的超声沿螺栓中轴传输,受应力集中以及螺纹等复杂结构影响小,具有结构简单、测量准确的优势,在不改变连接结构前提下,可实现螺栓预紧力长期在线监测,适用于复杂结构的可靠性评估。声弹性法是利用固体中声速随应力变化的现象检测应力。预先标定样品在不同应力下的声速,利用线性拟合获得应力与声速关系函数计算应力。声弹性分为纵波法[1]、横波法[2]、横纵波法、表面波法[3-4]以及临界折射纵波法[5]。在各种方法中,纵波声弹性法灵敏度最高[6],而且螺栓柱状形状适于纵波传播,因此,纵波声弹性法被广泛应用于螺栓应力测试。理论上,声速与应力呈线性关系,但在实际应用中存在非线性关系,而非线性关系直接影响应力测量的准确度。目前,声弹性法测试准确度最高为97%[7]。研究非线性误差来源是声弹性法向宽温、不定受力长度等测试条件推广的前提。针对声弹性螺栓应力测量应用及误差分析,前人均以应力均匀分布为前提,将误差归结为应力分布。张俊等[8-9]利用高强度螺栓开展实验,实验中声弹性误差达到5%。CHAKI等[10]利用横纵波结合法在无需确定受力长度情况下测量螺栓应力,认为样品直径影响应力测试灵敏度。DING等[11]采用电磁超声(EMAT)的方式产生超声纵波测量螺栓应力,认为实验结果中误差是由材料应力分布导致。CASTELLANO等[12]基于声弹性原理设计了新的表征参数,并在铁杆上开展声弹性实验,认为实验中产生的误差是由材料受力不均匀以及耦合层共同决定。针对前人的假设,本文作者首先以应力非均匀分布为前提建立声弹性测量模型,理论分析螺栓应力分布对声弹性测试影响;然后,采用ZnO压电薄膜激发超声纵波进行声弹性实验。压电薄膜与螺栓紧密贴合,在不增加探头体积的前提下克服了耦合层对测量的影响,实验的初始误差小于2%。实验采用变化螺栓受力长度以改变应力不均匀区占比,观察应力测量误差变化采用反复拉伸试验,分析材料损伤对应力测量误差的影响。
1 螺栓声弹性应力测量理论
1.1 微元的声弹性轴向应力时差法
超声测量固体应力是一种常用的无损检测方法。超声测量应力的方法包括超声反射强度法[13-14]、声弹性法[15]和非线性法[16]。其中,声弹性法测量准确度最高,它是通过超声传播时间测量应力。
微元声速与应力关系为
 (1)
(1)
式中:C为加载拉力后的声速;σ为应力强度;C0为未施加拉力的声速;k为声弹性系数。声弹性系数R由弹性体的各阶弹性模量与密度决定:
 (2)
(2)
式中:ρ0为密度;μ和λ为二阶弹性系数;m和l为三阶弹性系数。
C与C0无法直接获得,需利用微元长度和超声传播时间获得,建立传播时差与应力关系,即采用时差法测量应力。超声从头部传入螺栓,沿轴心传输并反射,因此,超声2次经过轴心微元。
 (3)
(3)
式中:L为微元长度;t0为无应力微元传播时间。
材料受力被拉伸,拉伸量由弹性模量E决定。受力后超声往返时间变为t。
 (4)
(4)
有应力与无应力超声传播时差△t为
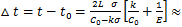
 (5)
(5)
声弹性系数k量级为10-11,金属声速量级为103。在10 MPa应力下,简化式(5)后引入的误差数量级仅为10-5。螺栓轴向应力σ正比于有应力和无应力状态下的声时差△t。以声弹性为基础,利用时差法可以测量螺栓轴向应力。
1.2 螺栓应力分布分析
时差法仅说明微元的时差与应力关系,为了获得总时差与应力关系,还需分析螺栓内应力分布。以剪力方式传入螺杆的螺栓支撑力与应力平衡,产生应力分布,如图1所示。

图1 螺栓应力分布
Fig. 1 Stress distribution of bolts
由图1可见:应力不均匀集中在螺栓头,远离螺头的微元应力不均匀减弱,最终趋于均匀分布,因此,分析螺栓头应力可获得整体应力分布。由于声弹性法测量超声沿螺栓中轴传输并反射的超声波速,该束声波不经过螺纹以及螺栓头部应力集中区,可忽略螺纹以及应力集中区的影响,对螺栓受力进行简化分析。由于轴对称结构,可以简化分析,选取螺栓轴心剖面的一半分析受力情况,如图2所示。图2中,H1为螺栓头的厚度,D1+D2为螺栓头的直径,D2为螺杆的半径。
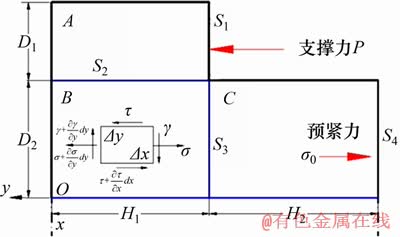
图2 螺栓内部应力关系图
Fig. 2 Stress diagram of bolts
在螺栓头部中心为原点建立坐标,S1,S2,S3和S4为不同区间的边界,将螺栓分为A,B和C这3个区间。S4上的应力σ0为螺杆中部均匀区的应力,为真实应力。S2上的τ是A和B两区之间的剪切力。S1上的P为基座对螺栓的支撑力。区间边界条件为:
1) C区边界H2足够长,S4上σ趋于均匀应力σ0;
2) 在螺栓顶面上(x=0)的切力τ与拉力σ为0;
3) S1的支撑力与S2的切力相同。
 (6)
(6)
质点在y轴方向(螺栓轴向)受力为
 (7)
(7)
得正应力与切应力关系:
 (8)
(8)
质点形变为u,则有
 (9)
(9)
式中:v为泊松比。利用分离变量法得
 (10)
(10)
根据式(9)得
 (11)
(11)
其中:
 (12)
(12)
 (13)
(13)
从式(11)可以看出σ和τ均呈关于x和y的指数分布。随着y负向增大,τ减小,σ增大,且σ和τ关于x方向趋于均匀分布。α决定非均匀区大小,α由弹性模量、泊松和头部的几何尺寸决定,与均匀区应力σ0无关。令x=0,得螺栓轴心上y方向应力分布:
 (14)
(14)
1.3 不均匀应力下的螺栓声弹性模型
声弹性螺栓应力测试中超声在螺杆轴心往复,如图3所示,因此,利用轴心应力分布结合时差法可以获得总时差与应力的表达式。螺母与螺头之间为受力区,其余部分为非受力区。非受力区声速恒定而不产生传播时差,整体时差只与受力区相关。

图3 螺栓中超声路径
Fig. 3 Ultrasound path in bolts
受力区螺母与螺头的对称结构,整体时差为受力区一半路径时差的4倍。将螺栓轴心应力分布代入时差法中,得到应力分布下的时差法与应力关系:
 (15)
(15)
式(15)表明声时差与应力呈线性关系,线性系数由螺栓材料和尺寸决定。应力分布不会造成传播时差的非线性。
在超声穿过应力非线性区情况下,时差法不产生非线性是因为应力非均匀区固定,且质点应力与均匀区应力呈线性关系。图4所示为ANSYS计算不同支撑力下轴心应力。根据质点时差法,轴心应力和横轴围成应力面积正比于传播时差。应力非均匀区固定,应力面积与均匀区应力呈线性关系。因此,均匀区应力正比于总时差。
图4 螺栓轴心应力仿真
Fig. 4 Stress simulation of bolt axle center
2 螺栓声弹性应力试验
2.1 超声脉冲产生
超声产生方式有压电陶瓷探头激发[17]、电磁脉冲探头(EMAT)激发和压电薄膜激发等。压电陶瓷需涂抹耦合剂增强超声注入,耦合剂厚度难以控制造成误差。EMAT是一种非接触测量,避免了耦合层的影响,但易受铁磁性物质影响,同时,系统复杂,降低了其实用性。采用ZnO压电薄膜产生超声,该方法结构简单,体积小,容易制备,工作温度宽泛,易得到高电阻率,在无耦合剂条件下,够保证测试重复性[18]。图5所示为超声压电收发器的结构。在室温真空环境下,首先,在M8×30 mm和M8×50 mm这2种研磨过的45号钢螺栓顶面上制备厚度大于1 μm的ZnO薄膜;然后,按版图制作金属电极。图6所示为制备ZnO压电薄膜后的螺栓样品。
图5 超声压电收发器的结构
Fig. 5 Structure of piezoelectric transceiver for ultrasound

图6 ZnO压电薄膜成品实物
Fig. 6 Photographs of ZnO piezoelectric films
2.2 声弹性应力实验测量
设计实验测试螺栓声弹性应力测量的准确度,图7所示为实验的结构图。首先,在螺栓与支撑面之间增加垫圈式力传感器,连接电源与数字多用表测量应力,力传感器测量准确度为0.5%。然后,测量超声在螺栓轴向的传播时间。测量传播时间的方法为:利用信号发生器激发ZnO压电薄膜,产生高频超声脉冲;超声脉冲经过受力的螺杆并由底部反射回压电薄膜,经过信号转换将发射波显示到示波器,利用相位检测技术[19]得到传播时间。最后,建立应力与传播时间的关系。

图7 螺栓声弹性应力测试系统
Fig. 7 Acoustoelastic stress testing system for bolts
2.3 测试结果
2.3.1 误差与非均匀应力的关系
测量2种样品的应力与超声在螺栓轴向传播时间,测量结果分别如表1和表2所示。
表1 M8×50 mm螺栓预紧力测试结果
Table 1 Test results of bolt proload (M8×50 mm)
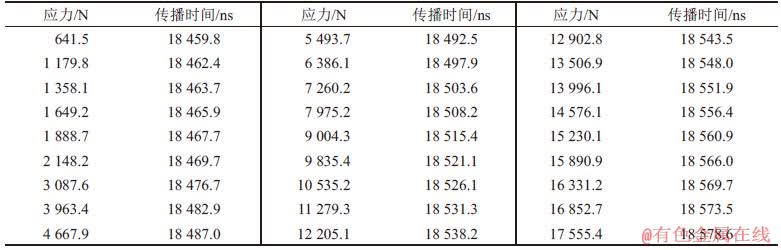
表2 M8×30 mm螺栓预紧力测试结果
Table 2 Test results of bolt proload (M8×30 mm)
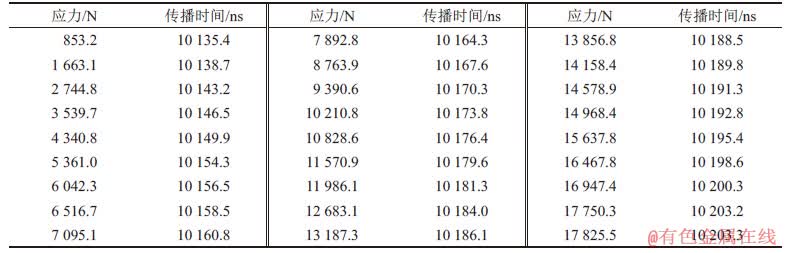
对表1和表2中的应力与传播时间进行处理,得到传播时差△t与应力σ0的关系如图8所示。由图8可见:2个样品随着应力增大,传播时差均呈近线性增加,但是比例关系不同,从而只需测量超声传播时间就可得到应力。
图9所示为样品声弹性应力测试误差,即力传感器测量值与计算值之差。由图9可见:螺栓应力误差与传播时间差无确定关系,进而说明螺栓应力误差与应力无关;2个曲线的误差最大值基本相同,约为250 N。这表明螺栓应力误差与非均匀区无关。若不均匀应力产生误差,则短螺栓不均匀区占超声路径的比重大,螺栓应力误差也应较大,但样品的最大误差相同,进而说明螺栓应力误差与应力分布无关。
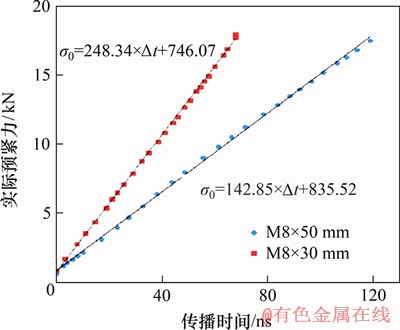
图8 2种样品声弹性测试结果
Fig. 8 Acoustoelastic test results of two samples
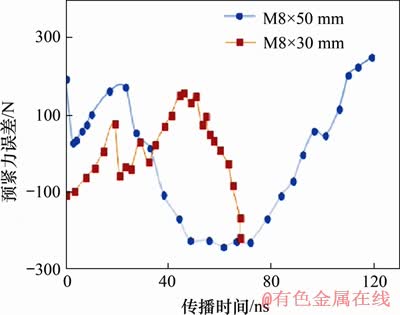
图9 声弹性应力误差
Fig. 9 Stress error of acoustoelastic effect
2.3.2 应力测量误差与材料损伤的关系
声弹性理论是基于材料各向同性的假设,但由于热处理等因素,实际材料已非理想材料。材料受力后微观损伤引起超声传播变化,产生应力测量误差。为测试材料对声弹性测试影响,多次高强度拉伸M8×50螺栓,然后测试声弹性应力测量误差,并与初始应力测量误差(图9)进行比较,验证材料对应力测量误差的影响。同时为了与不同长度螺栓的初始应力测量误差对应,对测试螺栓开展不同受力长度的比对试验,如图10所示。
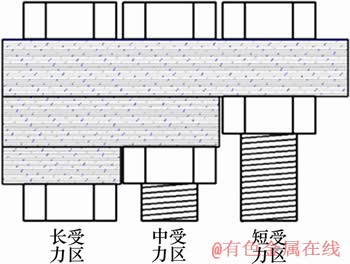
图10 同一样品不同受力长度测试
Fig. 10 Testing of different forced lengths for the same sample
不同受力长度的测试结果如图11(a)所示,由图11(a)可见:随着应力增加,传播时间增加;受力长度变短,应力与时差的比值变大,与理论计算结果相符合。图11(b)所示为3种受力长度的误差,中受力区螺栓应力测量长度误差最大,而短受力区螺栓应力测量长度误差最小,说明螺栓应力测量误差与非均匀应力分布相对超声路径的占比无关。经过多次拉伸后,声弹性应力测试误差增大,最大值高于1 000 N(低于5%)。分析其原因是螺栓为非理想材料的贝氏体或马氏体,经过反复拉伸,材料发生变化,产生缺陷(晶界滑移、错位增强),缺陷尺寸接近超声波长(约227 μm),超声在缺陷间反射、透射引起超声回波错乱,影响相位检测算法,产生误差。

图11 M8×50 mm螺栓不同受力长度测试结果
Fig. 11 Test results of different forecd lengths of bolt (M8×50mm)
3 结论
1) 基于螺栓声弹性测量方法,结合螺栓应力分布,建立应力分布条件下的时差法测量模型,得到应力与时差的关系,理论证明了应力分布与螺栓应力测量误差无关。
2) 提出采用 ZnO 压电薄膜进行声弹性测试的方法,验证了应力分布与非声弹性测量误差无关,样品的初始误差低于2%。
3) 材料的非均匀性是误差来源之一,缺陷和错位经过拉伸后扩大,增强了高频超声的散射,引起误差变大。
参考文献:
[1] JHANG K Y, QUAN Haihua, HA J, et al. Estimation of clamping force in high-tension bolts through ultrasonic velocity measurement[J]. Ultrasonics, 2006, 44: e1339-e1342.
[2] SCHRAMM R E. Ultrasonic measurement of stress in railroad wheels[J]. Review of Scientific Instruments, 1999, 70(2): 1468-1472.
[3] FUCHS P A, CLARK A V, LOZEV M G, et al. Ultrasonic instrumentation for measuring applied stress on bridges[J]. Journal of Nondestructive Evaluation, 1998, 17(3): 141-152.
[4] DUQUENNOY M, OUAFTOUH M, QIAN M, et al. Ultrasonic characterization of residual stresses in steel rods using a laser line source and piezoelectric transducers[J]. NDT & E International, 2001, 34(5): 355-362.
[5] ZHU Qimeng, CHEN Jia, GOU Guoqing, et al. Residual stress measurement and calibration for A7N01 aluminum alloy welded joints by using longitudinal critically refracted (LCR) wave transmission method[J]. Journal of Materials Engineering and Performance, 2016, 25(10): 4181-4189.
[6] HASEGAWA M, MATSUMURA J, KUSANO R, et al. Acoustoelastic effect in Melia azedarach for nondestructive stress measurement[J]. Construction and Building Materials, 2010, 24(9): 1713-1717.
[7] XU Chunguang, LI Xiao, PAN Qinxue, et al. Bolt stress measurements by ultransonic non-destructive methods[J]. Journal of Applied Acoustics, 2014, 33(2): 102-106.
[8] 张俊, 顾临怡, 钱筱林, 等. 钢结构工程中高强度螺栓轴向应力的超声测量技术[J]. 机械工程学报, 2006, 42(2): 216-220.
ZHANG Jun, GU Linyi, QIAN Xiaolin, et al. Ultrasonic measurement of high strength bolt axial tension in steel construction[J]. Chinese Journal of Mechanical Engineering, 2006, 42(2): 216-220.
[9] 贾雪, 王雪梅, 甘文成, 等. 声弹性效应螺栓轴向应力标定试验研究[J]. 中国测试, 2018, 44(3): 23-27.
JIA Xue, WANG Xuemei, GAN Wencheng, et al. Research on calibration of bolt's axial stress based on acoustoelastic effect[J]. China Measurement & Test, 2018, 44(3): 23-27.
[10] CHAKI S, CORNELOUP G, LILLAMAND I, et al. Combination of longitudinal and transverse ultrasonic waves for in situ control of the tightening of bolts[J]. Journal of Pressure Vessel Technology, 2007, 129(3): 383-390.
[11] DING Xu, WU Xinjun, WANG Yugang. Bolt axial stress measurement based on a mode-converted ultrasound method using an electromagnetic acoustic transducer[J]. Ultrasonics, 2014, 54(3): 914-920.
[12] CASTELLANO A, FRADDOSIO A, MARZANO S, et al. Some advancements in the ultrasonic evaluation of initial stress states by the analysis of the acoustoelastic effect[J]. Procedia Engineering, 2017, 199: 1519-1526.
[13] KUBE C M, TURNER J A. Stress-dependent second-order grain statistics of polycrystals[J]. The Journal of the Acoustical Society of America, 2015, 138(4): 2613-2625.
[14] 周晓军, 江月娟, 魏智, 等. 航空透明件表面应力声弹检测方法的实验研究[J]. 仪器仪表学报, 2000, 21(5): 497-500.
ZHOU Xiaojun, JIANG Yuejuan, WEI Zhi, et al. Experimental approach to the acoustoelastic method for surface stress testing of aerospace transparency[J]. Chinese Journal of Scientific Instrument, 2000, 21(5): 497-500.
[15] NUCERA C, LANZA DI SCALEA F. Nonlinear wave propagation in constrained solids subjected to thermal loads[J]. Journal of Sound and Vibration, 2014, 333(2): 541-554.
[16] Johnson, GC , Holt, AC , Cunningham, B. An ultrasonic method for determining axial stress in bolts[J]. Journal of Testing and Evaluation, 1986, 14(5): 253-259.
[17] ZHOU Q F, SHARP C, CANNATA J M, et al. Self-focused high frequency ultrasonic transducers based on ZnO piezoelectric films[J]. Applied Physics Letters, 2007, 90(11): 113502-113502-3.
[18] 钱莉荣, 杨保和. ZnO薄膜/金刚石在不同激励条件下声表面波特性的计算与分析[J]. 物理学报, 2013, 62(11): 478-489.
QIAN Lirong, YANG Baohe. Calculation and analysis of surface acoustic wave properties of ZnO film on diamond under different excitation conditions[J]. Acta Physica Sinica, 2013, 62(11): 478-489.
[19] ZHANG Han. Ultrasonic stress measurement with lfm lcr wave: theoretical verification and numerical simulation[C]. IEEE International Ultrasonics Symposium, 2014, 1352-1355.
(编辑 秦明阳)
收稿日期: 2019 -08 -01; 修回日期: 2019 -10 -20
基金项目(Foundation item):国家科技重大专项(2019ZX06002021) (Project(2019ZX06002021) supported by the National Science and Technology Major Program of the Ministry of Science and Technology of China)
通信作者:李明海,博士,研究员,从事装备环境试验和热安全性研究;E-mail: 231867903@qq.com