DOI: 10.11817/j.issn.1672-7207.2017.06.015

叶轮口环结构对离心泵性能及流场的影响

牟介刚¹，代东顺¹，谷云庆¹，刘剑¹，吴登昊²，马艺¹

(1. 浙江工业大学 机械工程学院，浙江 杭州，310014；

2. 浙江工业大学 之江学院，浙江 杭州，310024)

摘要：为了揭示叶轮口环间隙及结构型式对离心泵性能的影响，以IS80-65-160离心泵为模型载体，采用RNG k-ε湍流模型，对不同叶轮口环间隙及口环结构型式下的离心泵内部流场进行数值模拟，分析叶轮口环间隙对离心泵的效率、压力场和速度场的影响规律；研究3种环状结构型式的叶轮口环对离心泵性能的影响机制。研究结果表明：叶轮口环间隙的变化改变了离心泵内部流场的流动状态，影响其前、后泵腔处的压力分布，间隙内部的速度发生明显变化；锯齿形口环泄漏量最多可减少16.2%，容积效率提高，轴向力降低，锯齿形叶轮口环结构可提升离心泵2%的水力效率；流经两环状结构空腔的流体，过流面积增加，产生剧烈旋涡，并进行能量耗散，阻止了流体压力能的恢复，分散了经密封齿隙高速射出的流体的动能，间隙内部流体的速度梯度和压力梯度增大，湍动状态加剧，流动阻力增加。

关键词：离心泵；流体动力学；叶轮口环；结构型式；数值模拟

中图分类号：TB311             文献标志码：A         文章编号：1672-7207(2017)06-1522-08

Influences of impeller ring structure on performance and flow field of centrifugal pump

MOU Jiegang¹, DAI Dongshun¹, GU Yunqing¹, LIU Jian¹, WU Denghao², MA Yi¹

(1. College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China;

2. Zhijiang College, Zhejiang University of Technology, Hangzhou 310024, China)

Abstract: In order to study the impeller ring clearance and structural change effects on the performance of centrifugal pump, based on IS80-65-160 centrifugal pump, internal flow field for different impeller ring clearances and structures were numerically simulated through RNG k-ε turbulence model. The influences on efficiency, pressure field and velocity field were analyzed, and three kinds of impeller ring structures effect on the centrifugal pump were researched. The results show that impeller ring clearances changed the internal flow field of centrifugal pump and affected the pressure distribution of pump cavity. Among the three kinds of annularity structures, rectangle and serrated impeller ring can reduce leakage, (at most reduced by 16.2%), improve volumetric efficiency, balance action of axial thrust. Hydraulic efficiency increases by 2% after the change of impeller ring structure. When the fluid flows through the cavity between two rings, volume expansion and energy dissipation violently can prevent fluid restore its pressure, maximum dispersion the kinetic energy of high-speed injection fluid sealing from sealed gear. The internal fluid velocity gradient and pressure gradient are enlarged, and turbulent kinetic energy increases, and so the leakage is reduced.

Key words: centrifugal pump; hydrodynamics; impeller ring; type of construction; numerical simulation

离心泵是一种应用极广、种类甚多的通用机械，广泛应用于石油化工、动力工业、采矿和造船工业等。作为主要的输送设备之一，对其性能及稳定性的要求也在逐步提高。在把机械能转化为液体能量的过程中不可避免地伴有机械损失，冲击、脱流、速度方向急剧变化等引起的水力损失，以及液体从泵腔经叶轮密封环间隙向叶轮进口逆流产生的容积损失^[1]等，造成能量浪费。口环间隙密封是离心泵叶轮密封最常用的一种形式，口环间隙和结构会对离心泵的容积损失产生直接作用，并且改变了离心泵内部流场的流动状态，继而对离心泵的整机性能、轴向力、径向力等产生重要的影响。间隙流动作为目前流体机械研究的热点问题，离心泵口环间隙处流动状态复杂，口环间隙小，叶轮口环处的流动损失大^[2]。已有很多学者对此进行了研究，如：马文生等^[3]运用数值方法对转子-轴承密封系统动力学模型求解，研究了不同的密封间隙、密封直径、压差、入口损失率和密封长度对泄漏量和临界转速的影响，得到了泄漏量与密封间隙、密封直径和密封长度之间的关系。王炜哲等^[4]针对迷宫密封内作涡动旋转的转子承受腔室内周向不均匀压力，从而导致振动特性发生变化的问题进行了探讨。由于口环间隙尺寸的限制，计算网格划分困难，在现有的研究中一般只对叶轮、蜗壳等流体域进行研究而忽略口环间隙、结构变化对离心泵内部流场的影响，导致预测的效率与试验值之间存在较大的偏差，对计算模型的简化是造成偏差的主要原因^[5-6]。计算流体力学的发展，为分析离心泵的水力性能和改进泵的设计提供了有力的工具并且得到了广泛的应用^[7-10]。研究发现，在离心泵的高效区(设计流量的0.7~1.2倍)预测值和试验值基本吻合^[11-12]。为了进一步研究叶轮口环间隙及结构的变化对离心泵性能的影响，本文作者采用数值模拟的方法，建立离心泵全流体域计算模型，采用商用Fluent软件，分析了3种口环间隙和3种不同口环结构对离心泵泄漏量、轴向力、水力效率等特性的影响，揭示了离心泵内部流场的流动规律。

1  数值模拟方法

1.1  计算模型

以IS80-65-160离心泵为模型载体，计算模型如图1所示。计算模型主要包括进水管、出水管、叶轮、蜗壳、前后泵腔6个部分，其主要参数为：流量Q=50 m³/h，扬程H=32 m，转速n=2 900 r/min，进口直径D₁=80 mm，叶轮外径D₂=168 mm，叶片数为4。叶轮口环间隙长度l=15 mm、间隙宽度b=0.5 mm。

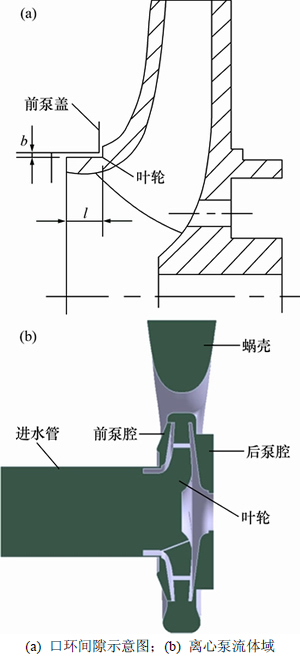
图1  计算模型

Fig. 1  Calculation model

1.2  求解器和控制方程

Fluent实际上是一个基于非结构化网格的通用求解器，本文采用3D单精度，基于压力的求解方法对计算模型进行求解，并运用多重旋转坐标系和有限体积法对非定常不可压缩N-S 方程进行离散，按顺序依次求解动量方程、压力修正方程、能量方程及其他标量方程，如湍流方程等。在流场求解时所用连续方程、动量方程和能量方程可以写成以下通用形式^[13-14]：

   (1)

式中：φ为通用因变量；S_φ为广义源项；u为速度矢量；Γ_φ为与φ相对应的广义扩散系数；ρ为流体密度；t为时间。

离心泵内部为复杂的三维湍流流动，故还需设置湍流模型，RNG k-ε湍流模型^[15]作为RANS方法中的一种形式，通过附加的湍动能k、耗散率ε、比耗散率ω等湍流量进行控制^[16]，考虑了湍流漩涡的影响，对强旋流动、脱流、漩涡等复杂流动的计算精度较高，更适用于对离心泵流场的数值模拟^[17-18]。

1.3  网格生成及边界条件设置

离心泵叶片、蜗壳等结构扭曲程度较高，网格质量将直接影响计算结果的准确性，非结构化网格对处理复杂问题具有很强的适应性，更适用于复杂模型的数值模拟。因此，本文运用ANSYS ICEM软件，采用Tetra/Mixed非结构化混合网格，对离心泵流体域进行分块网格划分，并对口环间隙处进行局部细化，使其内部具有足够的节点，以保证计算精度的要求。网格划分时，首先将口环间隙处的最大网格尺寸设为0.5，口环间隙内部的网格层数为2层；然后逐渐减小最大网格尺寸，当口环间隙处的最大网格尺寸为0.2时，口环间隙内部的网格层数为4层，离心泵流体域的总体计算网格数量在120万~220万范围内发生变化。流体域网格及叶轮口环间隙处的网格如图2所示。

为了检验网格划分及口环间隙处网格层数对数值计算结果的影响，分别选定6组不同的网格数进行数值模拟，分析网格的无关性。图3所示为标准工况Q=50 m³/h，口环间隙宽度b=0.5 mm时，不同网格数量对泄漏量和扬程影响的计算结果。由图3可知，当口环间隙内部网格层数为4，网格总数达到200万以后，随着网格数的增加，设计工况点的泄漏量q和扬程H变化较小，基本趋于稳定。因此在数值计算中，离心泵模型网格数量控制在200万上下波动，口环间隙内部网格层数为4层。

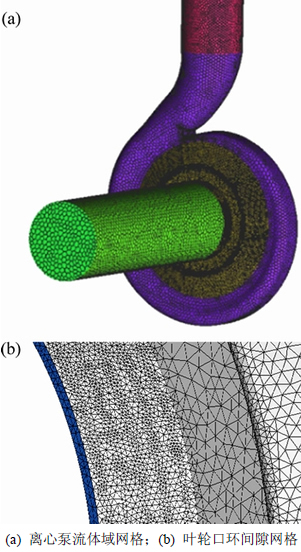
图2  离心泵流体域网格

Fig. 2  Meshes of centrifugal pump

图3  网格无关性检验

Fig. 3  Meshes independence test

离心泵流场计算域内的流体为不可压缩的牛顿流体，工作过程中流体的性质不发生变化，并且不考虑重力对流场的影响。模型进口为速度入口，出口为自由出流；近壁面采用标准壁面函数，壁面取不渗透、无滑移固体壁面边界条件，采用具有二阶精度的QUICK格式离散，压力修正为SIMPLC算法；计算过程中收敛精度设为1×10^-4，外界条件为常温常压，介质为水。在流量Q₀分别为0.8Q，1.0 Q和1.2Q等工况下，分别对离心泵的内部流动状态进行定常流动数值模拟。

2  口环间隙宽度对离心泵特性影响

离心泵的口环、多级泵的级间轴封、填料密封、轴向力平衡装置的动静部件之间都有液体的泄漏，使离心泵输出的液体体积减小并带走了部分功率。为了验证数值模拟结果的准确性，首先将不同口环间隙宽度情况下计算的模型水力效率与样机试验值进行对比，分析不同口环间隙宽度情况下离心泵的特性。其中样机口环间隙宽度为0.5 mm，数值计算模型的口环间隙宽度b分别为0.2，0.5和0.8 mm。离心泵水力效率的计算公式为

η_h=Q(p_in-p_out)/(1 000Mw)         (2)

式中：Q为实际流过叶轮的流量，m³/h；M为叶轮扭矩，N·m；w为叶轮转动角速度，rad/s；p_in和p_out分别为离心泵的进、出口压力，Pa。

离心泵水力效率试验值和模拟值的结果如图4所示。由图4可知：口环间隙的变化改变了离心泵的水力性能，不同口环间隙宽度下的模拟值和试验值之间均有不同程度的偏差，口环间隙宽度b=0.2 mm时，不同流量下的模拟值偏高；口环间隙宽度增大为0.8 mm时，模拟值则低于试验值；而当b=0.5 mm时，两者具有较好的一致性。在标准工况Q=50 m³/h下，口环间隙宽度由0.2 mm增加到0.8 mm的过程中，水力效率由76%下降到69%，降低了近7%。

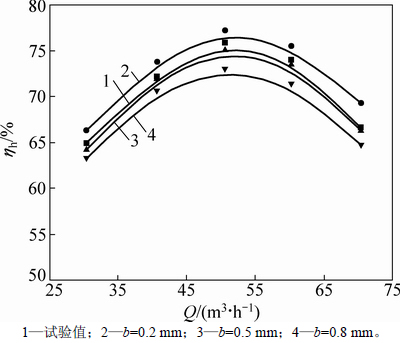
图4  不同口环间隙宽度下离心泵效率

Fig. 4  Efficiency with different impeller ring clearance widths

2.1  不同口环间隙宽度下离心泵压力场分析

图5所示为标准工况下，不同口环间隙宽度在Y=0平面的静压分布云图。由图5(a)可知：口环间隙宽度改变了泵腔的压力分布，其影响主要表现在前、后泵腔处；随着口环间隙宽度的增大，离心泵前泵腔的低压区向蜗室上移、扩大，后泵腔的高压区范围缩小；由于泵腔内轴向尺寸与径向尺寸之比很小，故压力分布只沿径向发生明显变化，且间隙宽度越小，前泵腔的压力梯度越明显。图5(b)所示为前泵腔的静压分布曲线。由图5(b)可知：前泵腔的压力随着半径的减小，呈线性降低的趋势，且随着口环间隙宽度的增大，其斜率不断增加；在3种不同间隙宽度的口环间隙中，泵腔进口处的压力相差不大，而在叶轮口环处，间隙宽度为0.2 mm时，流体的静压力明显高于其他间隙宽度下的压力。前泵腔压力的变化改变了流体的径向流动，间隙内部压力越高，流体流入叶轮口环时的阻力就越大，叶轮口环间隙高压区阻碍了流体向叶轮进口的泄漏。

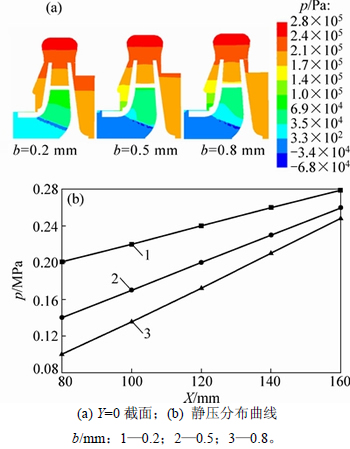
图5  不同口环间隙宽度下离心泵压力云图

Fig. 5  Contours of static pressure of different impeller ring clearance widens

2.2  不同口环间隙下离心泵速度场分析

在计算过程中，设△p为流体在叶轮口环流道进口压力p₀与出口压力p_l之差，流动方向上的长度为l，间隙宽度为b，则叶轮口环间隙流体平均速度u_m和压差流动的阻力系数λ的计算公式分别为：

               (3)

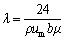                (4)

流体受到外部叶轮口环壁面剪切力的作用时发生变形流动，其内部产生对抗变形的抵抗，并以内摩擦力的形式表现出来。故叶轮口环间隙内部的流体同时具有沿周向的流动(前泵盖与叶轮的相对运动产生)及轴向的压力流动(前泵腔与叶轮进口的压差产生)。由式(3)和式(4)可知，离心泵口环间隙流体的流动速度对间隙宽度的变化更为敏感，当口环间隙宽度减小时，叶轮口环间隙流体平均速度u_m减小，阻力系数λ增大。图6所示为不同口环间隙宽度下，叶轮口环处的平均速度分布云图。由图6可知：在泵腔与叶轮进口压差作用下的高速流体通过叶轮口环间隙流向泵的进口，叶轮口环间隙宽度增大时，间隙内部的平均速度v增加，当口环间隙宽度b=0.8 mm，叶轮口环内部的平均速度约为13 m/s。因此，口环间隙宽度增大最终导致离心泵泄漏量的增加。

图6  不同口环间隙宽度的内速度场

Fig. 6  Contours of velocity in different impeller ring clearances

3  口环结构对离心泵特性影响

为了减小泄漏量对离心泵性能的影响，保持口环间隙长度l=15 mm不变，将口环间隙宽度增加到1.5 mm，并在叶轮口环上布置圆形、矩形和锯齿形环状结构，环状结构顶端距前泵盖的间隙宽度为0.5 mm(与原模型口环间隙宽度一致)。离心泵不同口环结构型式如图7所示，图中箭头为液体的流动方向，各类型环状结构的轴向间距为a=3 mm，高度h=1 mm。

3.1  泄漏量和容积效率分析

分析不同口环结构下离心泵性能的变化，取Q₀=0.8Q，1.0 Q，1.2Q 3个流量点，对间隙泄漏量、及容积效率进行计算，口环间隙泄漏量的基本计算公式为

             (5)

式中：A_a为间隙泄漏的过流面积，m³；△h_c1为液体流过密封间隙的损失水头，m；ζ为间隙损失系数；g为重力加速度。

则容积效率表示为

η_v=Q/(Q+q)               (6)

图8所示为不同结构口环下的间隙泄漏量q曲线。由图8可知：在不同流量下，离心泵泄漏量曲线变化趋势基本一致，均随着Q的增加，q呈先增加后减小的变化趋势；但在小于设计流量点时，泄漏量的变化趋势并不明显；圆形环状叶轮口环在3种工况下的泄漏量与其他形式的叶轮口环相比偏差较大，这可能与其流道内的流动状态有关，导致泄漏量增加，在标准工况下泄露量增加约30%。计算结果说明采用圆形环状叶轮口环时并没起到减小泄漏损失的作用；矩形和锯齿形的叶轮口环与原模型相比则具有较好的减小泄漏的效果，锯齿形结构的叶轮口环泄漏量最多可减少16.2%。

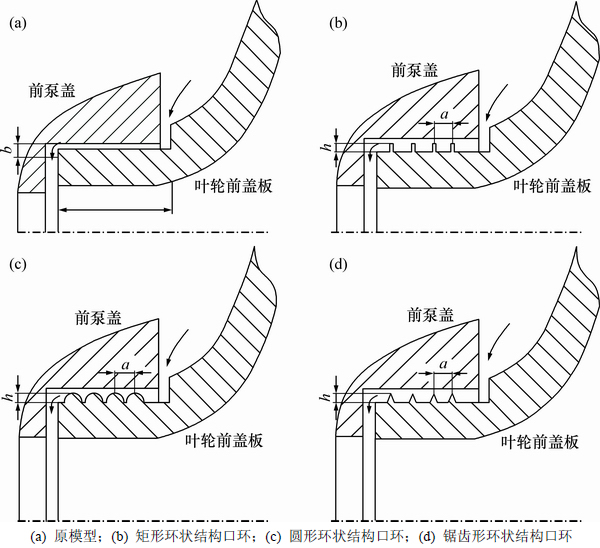
图7  不同结构离心泵口环

Fig. 7  Different structures of impeller ring

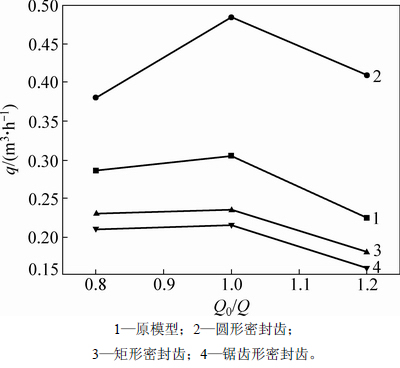
图8  不同结构口环泄漏量曲线

Fig. 8  Curves of leakage with different structures impeller ring

图9所示为不同叶轮口环结构的容积效率曲线。由图9可知：圆形叶轮口环在各工况下的容积效率均低于其他3种口环结构；锯齿形和矩形环状结构叶轮口环则均能有效提升离心泵的容积效率，且锯齿形叶轮口环的提升幅度更优于矩形结构；在不同工况下采用锯齿形叶轮口环时，离心泵的容积效率最高可提升3%。由此可知，口环间隙宽度虽然增加到了1.5 mm，但布置在叶轮口环上的锯齿形和矩形环状结构也能减小泄漏，提高容积效率。

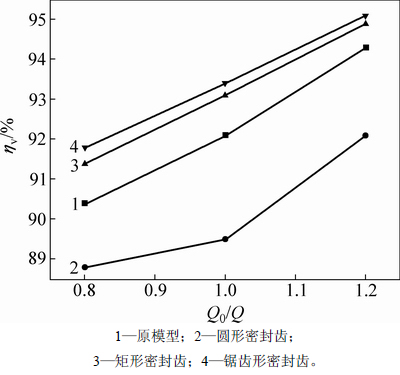
图9  不同结构口环容积效率曲线

Fig. 9  Curves of volumetric efficiency with different structures impeller ring

3.2  轴向力分析

图10所示为不同口环结构模型的轴向力曲线。由图10可知：不同工况下，4种口环结构下轴向力的变化趋势基本一致；对于同一叶轮口环结构的离心泵，轴向力均随着流量的增加而减小；同一流量点下，圆形叶轮口环离心泵的轴向力最大，矩形和锯齿形叶轮口环离心泵的轴向力均小于原模型，矩形环状结构口环平衡轴向力的效果最佳，轴向力最大减小10%。

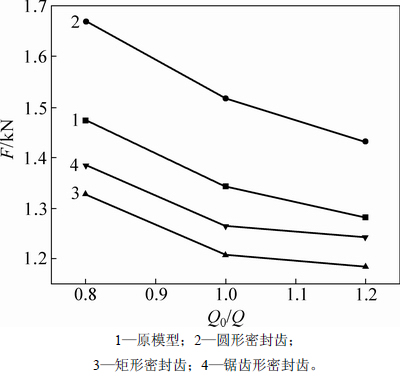
图10  不同结构口环轴向力曲线

Fig. 10  Curves of axial thrust with different structures impeller ring

图11所示为不同叶轮口环结构的离心泵在标准工况1.0Q下，Y=0截面的静压分布云图。由图11可知：锯齿形和矩形口环结构的叶轮前泵腔压力分布与口环间隙宽度为0.5 mm的原模型相比，低压区范围扩大且后泵腔的高压区范围缩小，而圆形环状结构的叶轮口环内部的压力分布并没有明显变化。圆形结构的叶轮口环，低压区的范围进一步缩小且后泵腔的高压区消失，故其轴向力不但没有减小反而增加。离心泵叶轮上的轴向力与前、后泵腔压力的变化密切相关，故锯齿形和矩形口环结构形式的密封口环可以起到平衡离心泵叶轮的轴向力的作用；同时口环间隙内部出现了较大的压力梯度，压力梯度的变化使流体的湍流脉动和雷诺应力增加，锯齿形和矩形口环结构改变了间隙内部流体的流动状态，促进了流体由层流流动向湍流流动的转变，流体的湍动能增加，实现了对流体的阻碍。

3.3  速度场分析

图12所示为不同叶轮口环结构下口环间隙的速度场分布云图。由图12(a)可知：在改变叶轮口环的结构后，两环状结构之间的空腔内存在明显的低速区，且从前泵腔到叶轮进口低速区的范围逐渐增大；速度从前泵腔到叶轮进口逐渐降低，与原模型口环相比，速度梯度的变化较为明显；一个环状结构和一个膨胀空腔构成了一级迷宫密封，当高速流动的流体遇到环状结构的阻碍后进入节流齿隙，导致流体的湍动状态加剧；压力推动流体由高压侧流向低压侧，流体流过节流齿隙，由于流道变窄，流速增高，压力降低，压力能转变为动能。以矩形结构叶轮口环间隙为例，流动状态如12(b)所示，流体以高速进入两环状结构之间的空腔时，过流面积突然增加，流速降低，并产生剧烈旋涡，有效阻止了流体压力能的恢复，最大程度地分散经密封齿隙高速射出的流体的动能；在压力梯度作用下，流体将会产生回流形成边界层分离；从下游回流的液体受到主流的冲击折返流向下游，在分离点形成漩涡和尾流区，尾流区的漩涡使流体的阻力剧增，减小叶轮口环间隙的泄漏。

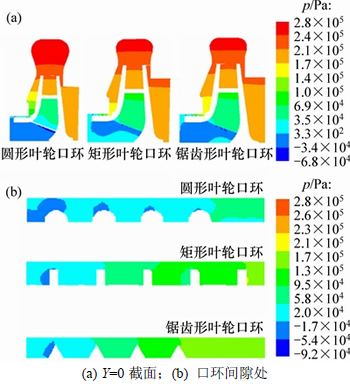
图11  不同口环结构下离心泵压力场

Fig. 11  Contours of static pressure with different structures impeller ring

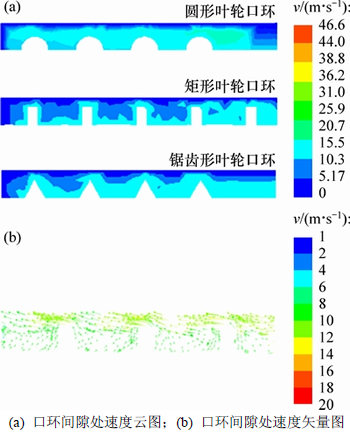
图12  不同口环结构下的速度云图

Fig. 12  Velocity field of different structures impeller ring

4  结论

1) 口环间隙宽度的变化改变了离心泵前后泵腔的压力分布，口环间隙增大，前泵腔的低压区向蜗室上移、扩大，后泵腔的高压区范围缩小；间隙内部流体的速度随间隙的增大而增加，容积效率下降。

2) 口环间隙宽度增大到1.5 mm的情况下，锯齿形和矩形环状结构叶轮口环均能明显减小泄漏量，最多减少16.2%，不同工况下采用锯齿形叶轮口环时，离心泵的容积效率最高可提升3%。

3) 在不同结构的口环中，圆形叶轮口环离心泵的轴向力最大，矩形和锯齿形叶轮口环离心泵的轴向力均小于原模型，矩形环状结构口环平衡轴向力的效果最佳，轴向力最大减小10%。

4) 环状结构叶轮口环改变了离心泵口环间隙内部流体的流动状态，矩形和锯齿形状结构之间的空腔内存在明显的低速区，间隙内部速度梯度、压力梯度增加，实现了增加流体流动阻力的作用，最终导致离心泵口环处泄漏量减小，容积效率提高。

参考文献：

[1] 周凌九, 王占民, 江东智, 等. 离心泵非定常流动计算及性能预测[J]. 排灌机械工程学报, 2010, 28(4): 286-290.

ZHOU Lingjiu, WANG Zhanmin, JIANG Dongzhi, et al. Computation of unsteady flow and performance prediction for centrifugal pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2010, 28(4): 286-290.

[2] 吴大转, 许斌杰, 武鹏, 等. 多级离心泵内部间隙流动与泄漏损失[J]. 浙江大学学报, 2011, 45(8): 1393-1398.

WU Dazhuan, XU Binjie, WU Peng, et al. Internal clearance flow and leakage loss in multistage centrifugal pump[J]. Journal of Zhejiang University, 2011, 45(8): 1393-1398.

[3] 马文生, 陈照波, 焦映厚, 等. 迷宫密封结构对泄漏量和轴系临界转速影响分析研究[J]. 振动工程学报, 2013, 26(6): 823-830.

MA Wensheng, CHEN Zhaobo, JIAO Yinghou, et al. Leakage and critical speed effect of labyrinth seal structure[J]. Journal of Vibration Engineering, 2013, 26(6): 823-830.

[4] 王炜哲, 刘应征, 叶春, 等. 迷宫密封-转子系统动力学特性的试验测量和数值模拟[J]. 机械工程学报, 2007, 43(3): 22-27.

WANG Weizhe, LIU Yingzheng, Ye Chun, et al. Experimental measurement and numerical simulation of dynamics of labyrinth seal-rotor combination[J]. Journal of Mechanical Engineering, 2007, 43(3): 22-27.

[5] LUCIUS A, BRENNER G. Unsteady CFD simulation of a pump in part load conditions using scale-adaptive simulation[J]. International Journal of Heat and Fluid Flow, 2010, 31(6): 1113-1118.

[6] BENIGNI H, JABERG H, YEUNG H, et al. Numerical simulation of low specific speed american petroleum institute pumps in part-load operation and comparison with test rig results[J]. ASME Journal of Fluids Engineering, 2012, 134(2): 024501.

[7] 李晓俊, 袁寿其, 潘中永, 等. 基于结构化网格的离心泵全流场数值模拟[J]. 农业机械学报, 2013, 44(7): 50-54.

LI Xiaojun, YUAN Shouqi, PAN Zhongyong, et al. Numerical simulation of whole flow field for centrifugal pump with structured grid[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(7): 50-54.

[8] 谭磊, 曹树良, 桂绍波, 等. 带有前置导叶离心泵空化性能的试验及数值模拟[J]. 机械工程学报, 2010, 46(18): 177-182.

TAN Lei, CAO Shuliang, GUI Shaobo, et al. Experiment and numerical simulation of cavitation performance for centrifugal pump with inlet guide vane[J]. Journal of Mechanical Engineering, 2010, 46(18): 177-182.

[9] LUCIUS A, BRENNER G. Numerical simulation and evaluation of velocity fluctuations during rotating stall of a centrifugal pump[J]. Journal of Fluids Engineering, Transactions of the ASME, 2011, 133(8): 1-8.

[10] ZHANG Y L, Li Y, CUI B L, et al. Numerical simulation and analysis of solid-liquid two-phase flow in centrifugal pump[J]. Chinese Journal of Mechanical Engineering, 2013, 26(1): 53-60.

[11] 周岭, 施卫东, 陆伟刚, 等. 深井离心泵数值模拟与试验[J]. 农业机械学报, 2011, 42(3): 69-73.

ZHOU Ling, SHI Weidong, LU Weigang, et al. Numerical simulation and experiment on deep-well centrifugal pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(3): 69-73.

[12] 袁寿其, 徐宇平, 张金凤, 等. 流固耦合作用对螺旋离心泵流场影响的数值分析[J]. 农业机械学报, 2013, 44(1): 38-42.

YUAN Shouqi, XU Yuping, ZHANG Jinfeng, et al. Numerical analysis for effect of fluid-structure interaction on flow field in screw centrifugal pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(1): 38-42.

[13] 谷云庆, 牟介刚, 代东顺, 等. 基于蚯蚓背孔射流的仿生射流表面减阻性能研究[J]. 物理学报, 2015, 64(2): 310-319.

GU Yunqing, MOU Jiegang, DAI Dongshun, et al. Characteristics on drag reduction of bionic jet surface based on earthworm’s back orifice jet[J]. Physica Sinica, 2015, 64(2): 310-319.

[14] GU Yunqing, ZHAO Gang, ZHENG Jinxing, et al. Experimental and numerical investigation on drag reduction of non-smooth bionic jet surface[J]. Ocean Engineering, 2014, 81: 50-57.

[15] MOUTAOUAKIL L E, ZRIKEM Z, ABDELBAKI A. Performance of various RANS eddy-viscosity models for turbulent natural convection in tall vertical cavities[J]. Heat and Mass Transfer,2014, 50(8): 1103-1113.

[16] SONG X G, Park J, KIM S G, et al. Performance comparison and erosion prediction of jet pumps by using a numerical method[J]. Mathematical and Computer Modeling, 2013, 57(1): 245-253.

[17] DING H, VISSER F C, JIANG Y, et al. Demonstration and validation of a 3D CFD simulation tool predicting pump performance and cavitation for industrial applications[J]. ASME Journal of Fluids Engineering, 2011, 133(1): 1-14.

[18] 林琳, 王言英. 不同湍流模型下圆柱涡激振动的计算比较[J]. 船舶力学, 2013, 17(10): 1115-1125.

LIN Lin, WANG Yanying. Comparison between different turbulence models on vortex induced vibration of circular cylinder[J]. Journal of Ship Mechanics, 2013, 17(10): 1115-1125.

(编辑  赵俊)

收稿日期：2016-06-30；修回日期：2016-09-07

基金项目(Foundation item)：国家自然科学基金资助项目(51406183)；浙江省自然科学基金资助项目(LQ15E050005)；中国博士后科学基金资助项目(2016M601736)(Project(51406183) supported by National Natural Science Foundation of China; Project(LQ15E050005) supported by Zhejiang Provincial Natural Science Foundation of China; Project(2016M601736) supported by the China Postdoctoral Science Foundation)

通信作者：谷云庆，博士，硕士生导师，从事离心泵流场理论研究；E-mail：guyunqing@hrbeu.edu.cn