DOI: 10.11817/j.issn.1672-7207.2015.12.048
纤维表面气溶胶粒子对流扩散沉积行为随机模拟
吴世先1, 2，朱辉1, 2，付海明2，亢燕铭2
(1. 桂林航天工业学院 建筑环境与能源工程系，广西 桂林，541004；
2. 东华大学 环境科学与工程学院，上海，200051)
摘要：采用离散随机模拟方法模拟平行排列纤维表面超细气溶胶粒子的对流扩散沉积过程。以Kuwabara流场近似描述纤维附近区域流体的绕流特征，基于格子随机游走方法求解粒子对流扩散输运方程，以获得粒子在计算区域的运动概率。讨论纤维表面粒子沉积形成粉尘层的动态过程和粉尘层的形态结构特征与粒子输运机制的关系。研究结果表明：粉尘层的形态结构主要依赖于粒子的输运机制，以扩散输运机制主导(多因素归一参量Pe＜10)的粒子沉积过程将形成更为开放、松散的粉尘层结构；粒子沉积过程表现出粉尘黏附、粉尘树枝桥接和滤饼生长3个阶段；依据粉尘层填充率随粉尘层厚度的变化关系，粉尘层可分为滤饼基层、滤饼主体层和滤饼表层3个典型结构。
关键词：纤维过滤；粒子沉积；对流扩散；粉尘层
中图分类号：TQ021；TU834；X701.2 文献标志码：A 文章编号：1672-7207(2015)12-4738-09
Stochastic simulation of convective diffusional deposition of ultrafine particles on surface of fibers
WU Shixian1, 2, ZHU Hui1, 2, FU Haiming2, KANG Yanming2
(1. Department of Building Environment and Energy Engineering,
Guilin University of Aerospace Technology, Guilin 541004, China;
2. School of Environmental Science and Engineering, Donghua University, Shanghai 200051, China)
Abstract: A discrete stochastic model was developed to simulate the convective diffusional deposition of ultrafine particles in a model filter composed of an array of identical parallel fibers placed transverse to the flow. The flow feature in the vicinity of fibers was described by the Kuwabara flow field. Lattice walk method was employed to solve convection-diffusion-migration equation in order to obtain the probability of particle motion in the calculation domain. The local structures of dust layer formed by deposited particles and the relationship between structure of dust layer and mechanisms of particle transport were investigated. The results show that for Pe<10, when the diffusion is a controlling mechanism of particles transport, dust layer is more open and looser structure than that obtained at the higher value of Pe. The whole particles deposition process may be distinguished by three stages of particles adhesion, particles bridging and dust layer growth. According to the change of locate packing density along the dust layer height direction, the structure of dust layer can be divided into three typical parts of substructure, main profile and surface layer.
Key words: fibrous filtration; particle deposition; convection-diffusion; dust layer
随着我国电力、建材、冶金、化工、矿业等重工业的迅速发展，大量颗粒物的排放导致了灰霾天气、酸雨和气候变化等重大环境问题[1-3]。目前基于纤维过滤技术的袋式除尘是控制微粒排放并完全达到国家环保标准的有效手段之一。在袋式除尘的操作过程中，含尘气体的微粒在滤料表面沉积形成粉尘层，从而引起过滤性能(过滤效率和过滤压降)变化，并最终导致过滤设备失效[4-5]。为实现除尘设备在设计和操作条件上的优化，则需要获得粉尘层形态结构特性与操作条件之间的关联信息。在有关粉尘层形态结构特性研究方面，Myojo等[6-8]以单根纤维为研究对象观察了纤维表面粒子在对流扩散、惯性碰撞及静电场耦合作用下的多机理沉积行为；Kasper等[9-10]则采用更精细的实验手段研究了平行排列纤维表面粒子在惯性碰撞和反弹作用下的沉积行为，并定量测定了沉积物的孔隙率；Penicot等[11-14]以实际纤维滤料为研究对象，从宏观角度考察了过滤压降与沉积量的关系。这些实验结果充分证实了过滤操作条件对粉尘层形态结构演变起主导作用，而粉尘层形态结构则反过来又影响过滤特性。为寻求过滤操作条件对粉尘层形态结构演变机理的理论解析，Kanaoka等[15-18]采用随机模拟方法模拟了单根纤维表面粒子受控于各类沉积机理下的沉积行为，在此基础上，朱辉等[19]采用随机模拟方法动态再现了单纤维表面粒子的沉积过程，并给出了该过程更为真实的三维物理图像；Stocklmayer等[20-21]考虑了粒子间的滑移压缩行为，在二维空间模拟了平行排列纤维表面粒子惯性碰撞沉积过程，并解析了粉尘层生长过程中局部孔隙变化特性，但其忽略了粒子的对流扩散作用及纤维附近流体的绕流特征，因此该模型适应于惯性粒子沉积情形。在此基础上，本文作者针对平行排列纤维表面超细粒子的对流扩散沉积机理，进一步探索粒子沉积行为及沉积物的形态特性。
1 物理数学模型
考虑二维空间下纤维滤料表面的粒子对流扩散沉积过程，将真实随机排列的复杂纤维结构简化为平行排列结构，如图1所示。采用Kuwabara修正流型近似描述纤维附近的绕流特征，而处于Kuwabara流场作用以外计算区域则假定为直线流。计算粒子在远离纤维表面的粒子释放面上随机放置，在对流和扩散耦合输运机制作用下输送至纤维表面和已沉积粒子附近而沉积。
考虑实际过程中粒子与流体，粒子与纤维以及粒子之间动力学行为的复杂性，对粒子相作如下基本假设：1) 考虑粒子相为稀相，粒子与气相之间作用为单向耦合，即粒子的存在不对计算区域的流场产生影响；2) 假定进入计算区域粒子具有相同物性参数的单分散球形粒子；3) 忽略粒子所受的重力、静电力及分子作用力等，仅考虑粒子受流体曳力和布朗随机力作用；4) 忽略沉积物存在对流场畸变的影响，并认为粉尘层在流场中不发生倒塌、倒伏及断裂等重构动力学行为。
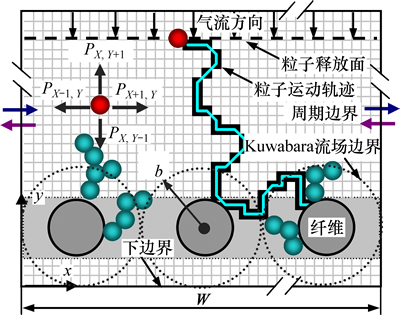
图1 模拟模型
Fig. 1 Simulated model
在上述假定条件下，纤维表面粒子输运方程为
(1)
式中：ux和uy分别为x和y方向的气流速度，m/s；n为计算空间单位体积中粒子数，个/m3；Dx和Dy分别为x和y方向的粒子扩散系数，m2/s。式(1)中的前2项为扩散项，第3项和第4项分别为x和y方向的对流项；假设粒子的扩散系数具有各向同性(即Dx=Dy=Dp)，Dp由下式给出[2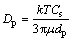2]
(2)
式中：k为Boltzmanm常数，k=1.38×10-23 J/K；T为热力学温度，K；dp为粒子直径，m；m为空气的动力黏度，Pa×s；Cs为Cumningham滑移修正系数[23]，且
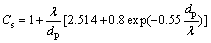(3)
式中：λ为空气分子平均自由程。由分子运动论的相关理论推导出[2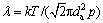4]
(4)
式中：da为空气分子平均直径，m；p为空气压强, Pa。
为方便求解，引入如下量纲一的量：
；
；
；
；
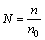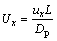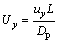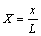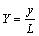(5)
式中：L为特征长度；n0为主流气体中的粒子浓度。将式(1)两边同除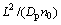
，则粒子的输送方程可改写为如下量纲一的形式：
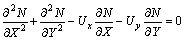(6)
令δX=δX=Δ，采用中心差分格式将式(6)作离散化处理后，其形式为
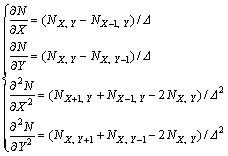(7)
将式(7)代入式(6)得
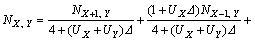
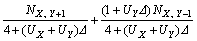(8)
设当前粒子的空间位置为(X, Y)，则下一时刻粒子在各方向的迁移概率分别为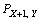
，
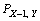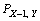，和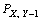
。
由文献[25-26]可知：粒子迁移概率与粒子浓度存在如下关系：
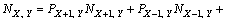
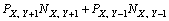(9)
对比式(8)和式(9)可以获得二维空间下粒子在各方向的迁移概率为
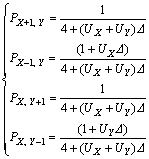(10)
式(10)表明：求解粒子迁移概率需要获得计算区域的流场信息。在分析时，若均忽略纤维附近的绕流作用，即假定流体作直线运动，则会丢失纤维附近区域有关粒子沉积行为的重要信息。因此，这里考虑采用Kuwabara修正流场来描述纤维附近的流场特征，而在Kuwabara流场作用以外区域仍采用直线流的假设。柱坐标系下Kuwabara修正流场的流函数[27-28]可表达为
(11)
式中：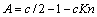
；
；
；
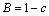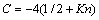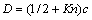；Kn为Knudsen数，
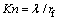；rf为纤维半径，m；u为表观速度，
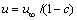，m/s；u∞为主流平均速度(即过滤风速)，m/s；c为过滤单元容密度，定义为纤维体积与Kuwabara过滤单元体积比(亦称过滤单元填充密度)，
；b为Kuwabara流场单元半径(见图2)，m；r为径向坐标；θ为极坐标。
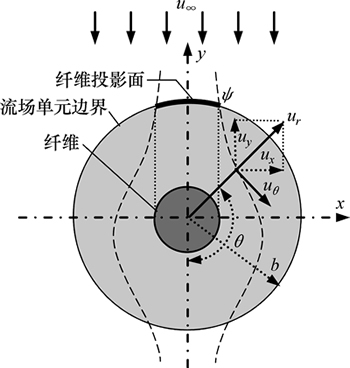
图2 Kuwabara流场结构示意图
Fig. 2 Schematic diagram of Kuwabara flow configuration
为求解方便，将柱坐标系下的Kuwabara流场速度分量转换为直角坐标下的速度分量，根据图2中两坐标系的流场速度关系，可得直角坐标下x和y方向的速度分量为
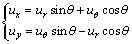(12)
式中：
；
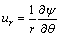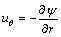(13)
数值求解时，假定粒子的初始位置在释放平面上随机产生(见图1)，一旦粒子的初始位置确定后，则粒子按照式(10)给出的迁移概率在计算区域运动。若粒子与纤维或已沉积粒子发生碰撞，则粒子黏附；当粒子运动至计算区域下边界时，则终止追踪该粒子，重新在释放平面上随机产生新的粒子。若粒子运动至周期边界时，则该粒子以相同运动方向从另一周期面上相同y处进入计算区域。粒子沉积形成粉尘层的模拟计算过程如图3所示。
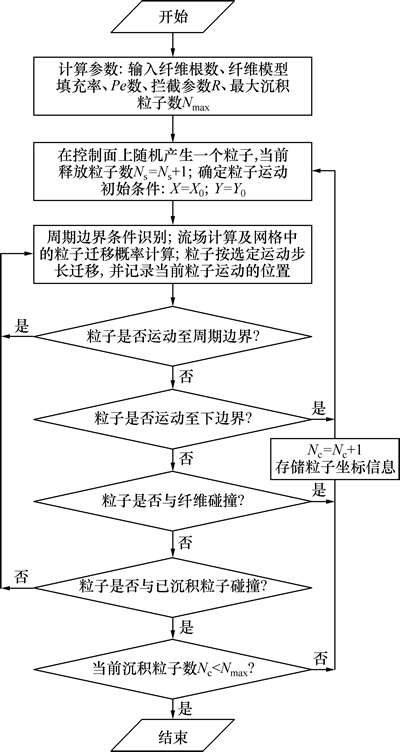
图3 计算流程图
Fig. 3 Flow chart of calculation
2 结果与讨论
由式(10)可知：粒子迁移概率取决于量纲一的量Ux和Uy。注意到Ux和Uy表达式中ux和uy是由Kuwabara流场决定的，故可考虑引入新的量纲一的参数Pe=u∞L/Dp作为反映影响粒子迁移概率的多因素归一参量。Pe定义式的分子反映了对流作用，分母则反映了粒子扩散作用。若取Pe
∞，则粒子输运机制完全由流体对流作用主导，粒子的扩散输运机制可以忽略；若Pe0，则粒子将做作纯扩散运动，流体对粒子的对流输运作用消失。为方便与其他研究者结果进行比较，Pe表达式中的特征长度与其他研究者选取原则一致(L=rf)，过滤单元容密度c=0.2，粒子直径与纤维直径比值(亦称拦截参数)取为R=0.2(R=dp/(2rf))。为取得合理的计算时间和捕捉到粒子与纤维及粒子之间碰撞时精细的几何信息，经试算确立粒子运动计算步长为0.1×dp。分析该计算步长条件下的粉尘层形态结构(见图4)，未发现粒子间存在重叠现象，而过小的运动步长导致了计算时间的急剧增加。计算区域长度W对粉尘层孔隙结构有一定影响，若计算区域长度W取值过小，则相同模拟参数下执行不同模拟事件而获得的粉尘层孔隙参数将会因粒子运动的随机特征及边界效应而出现较大波动。为获得较为稳定的粉尘层孔隙参数，采用逐步增加计算区域长度直至获得较为稳定的粉尘层孔隙参数。按此方案确立的纤维数为10根。
2.1 数值模型验证
为验证模型的可靠性，选取平行排列纤维中1根纤维作为计算对象，如图2所示。设通过纤维投影面积内的粒子数为Ms，被纤维捕集的粒子数为Mc，则单纤维捕集效率计算式为
(14)
单纤维捕集效率h与Pe的关系曲线如图4所示。作为对比，图中还给出了Lee等[29-30]的研究结果。
由图4可知：对于点粒子扩散情形(R=0)，当Pe＜1 000时，本文的计算结果与Lee等[29]的理论解较吻合，但略高于Rao等[30]的数值计算结果；而当Pe＞1 000时，本文计算结果与Rao等[30]的结果较为接近，而Lee等[29]的计算值明显低于本文的结果，并随着Pe的增大，Lee等[29]的结果与本文计算结果偏差进一步增大。当考虑拦截和扩散捕集机理共同作用时(R=0.2)，当Pe较大时(Pe＞1 000)，本文计算结果与Lee等[29-30]的结果均较吻合，而当Pe较小时(Pe＜1 000)，本文计算结果均略高于Lee等[29-30]的计算值。三者计算结果存在偏差的原因可能是各自模型计算中所采用的流场细微差异造成的，Lee等[29]采用的是标准的Kuwabara流场，而本文采用是考虑了纤维表面气流滑移作用的Kuwabara修正流场，Rao等[30]则是直接求解N-S方程获得纤维附近流场。
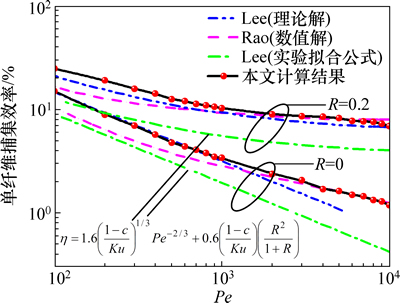
图4 单纤维捕集效率计算结果与其他理论结果比较(c=0.1)
Fig. 4 Comparison of single fiber efficiency due to interception and diffusion with other theories (c=0.1)
为验证单纤维扩散捕集效率理论预测的准确性，将Lee等[29-30]及本文给出的单纤维扩散捕集效率理论预测值与Lee等[29]的实验拟合公式进行比较(见图4)。由图4可见：三者的理论预测值均高于Lee等[30]的实验值，这可能是实验工况条件不完全满足理论模型的假设造成的。理论模型要求过滤气流方向垂直于纤维且纤维为等间距交错排列，而实际过滤器中纤维为随机排列，因此纤维在过滤器中的分布及方向并不完全与理论模型一致。纤维分布的不均匀性将导致过滤器中局部孔隙增大，粒子有可能直接穿透过滤器。而过滤气流非垂直于纤维情形直接降低了纤维捕集粒子的有效面积。尽管本文的单纤维捕集效率计算值与其他研究者的理论值及实验结果存在一定的偏差，但模型计算可靠性仍在可接受范围。
2.2 粉尘层动态生长过程描述
在确认计算模型可靠性后，在原有程序基础上考虑粒子之间的碰撞黏附作用，便可模拟出粒子动态沉积过程及粉尘层形态结构的物理图像。为比较粒子输运机制对粉尘层形态结构的影响，选取Pe=10和Pe=5 000这2种情形进行模拟，结果如图5所示。
图5表明：2种情形下粒子沉积行为均表现出粉尘黏附、粉尘树枝桥接和滤饼生长3个沉积阶段。在粉尘黏附阶段，粒子主要与纤维体发生碰撞黏附作用；一旦粒子被纤维捕集，则该粒子将成为后续粒子进一步沉积的基点，并以树枝状生长形式沉积，直至与邻近纤维上的粉尘树枝桥接形成网状的多孔结构，这一阶段称为粉尘树枝桥接阶段。当纤维间的粉尘树枝发生桥接后，则纤维捕集粒子的能力将消失，粒子的捕集将完全由粒子自身来完成，此时，粒子沉积过程进入滤饼生长阶段。此外，由图5可以看到：Pe分别为10和5 000时，粉尘层结构存在显著差异，Pe=10时，粉尘树枝在空间的延伸区域较大，且粉尘层具有更开放、更松散的结构。
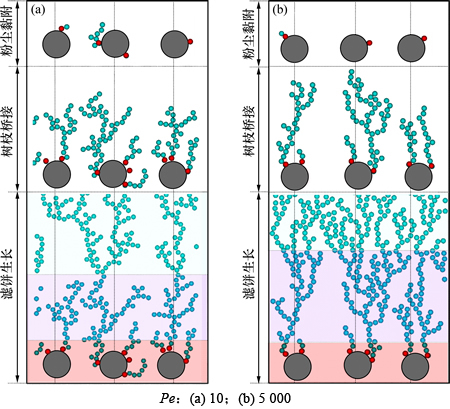
图5 Pe=10和Pe=5 000时粉尘层形态结构
Fig. 5 Simulated morphological structure of dust layer for Pe=10 and Pe=5 000
为说明不同Pe下沉积物形态结构差异的内在机制，分别计算出不同Pe下粒子的运动轨迹(见图6)。由图6可见：Pe=10时粒子的运动轨迹表现出强烈的随机游走特性，这意味着处于粉尘树枝梢端的粒子具有更大的概率与来流粒子发生黏附作用，粉尘树枝的生长将呈现出“非均衡”性。而Pe=5 000时的粒子运动轨迹几乎追随流体运动。由前面的讨论可知：此时，粒子输运机制为对流作用主导，粒子的沉积位置取决于粒子的初始位置，又因为粒子的初始位置为均匀随机分布。因此，从统计意义上看，沉积物上各点接触到来流粒子的概率均等，在滤饼生长阶段沉积物孔隙结构也就表现出较为均匀的特征。由此可见，粒子的输运机制是通过粒子的运动轨迹对沉积物形态结构产生影响。
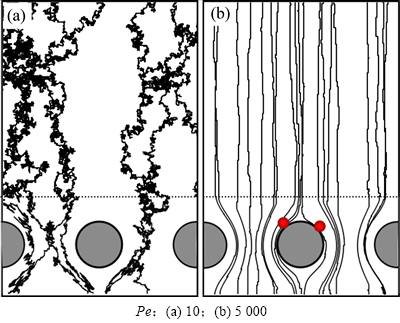
图6 Pe=10和Pe=5 000时粒子运动轨迹特征
Fig. 6 Characteristics of particle trajectories for Pe=10 and Pe=5 000
为定量分析粒子的沉积行为，图7所示为3种Pe数情形下沉积粒子数Nc和释放粒子数Ns的关系曲线。由图7可知：Pe=5 000时，Nc-Ns的关系曲线反映了前文对粒子3个阶段性沉积过程的分析结果。在粉尘黏附阶段，因粒子的捕集效率较低，沉积粒子数Nc随释放粒子数Ns增加缓慢；随着沉积粒子数的进一步增加，粉尘树枝结构开始生长并对粒子捕集起主要贡献，因此沉积粒子数Nc随释放粒子数Ns迅速增加；当粉尘树枝桥接结束时，粒子沉积过程进入滤饼生长阶段，几乎所有来流粒子均被沉积粒子捕集，此时沉积粒子数Nc随释放粒子数Ns呈线性增加关系。Song等[5]在电镜观察实际纤维过滤器内粒子沉积行为时，也发现了与本文理论分析较为一致的结果。但也注意到：随着Pe减小，粉尘黏附和粉尘树枝桥接2个阶段特征越不明显，对于Pe=10时，这2个阶段几乎无法察觉。这是由于Pe越小，粒子被纤维捕集效率越大，在释放粒子数较少条件下即可完成前2个阶段，从而使粒子沉积过程较早地进入滤饼生长阶段。
2.3 粉尘层孔隙结构描述
粉尘填充率是描述粉尘层孔隙结构的重要参量，亦是影响系统过滤压降及其他与过滤性能相关的粉尘层动力学行为(如粉尘层倒塌、压缩行为)的关键参量。因此，分析粒子输运机制对粉尘层填充率变化特性的影响十分必要。粉尘填充率ρc定义为某一采样粉尘层中粒子与粉尘层体积比。取一个粒子直径高度作为沿粉尘层厚度方向(即y方向)局部填充率计算的采样层厚度，沿垂直x-y平面方向粉尘层采样层厚度亦为一个粒子直径(如图8(b)所示)，则有
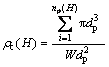(15)
图7 沉积粒子数Nc和释放粒子数Ns的变化关系
Fig. 7 Relationship between number of deposited particles and number of released particles
式中：np(H)为采样层中的粒子数。若平行排列纤维根数为nf，过滤单元容密度为c，则由图1中给出的物理参量意义及式(11)中定义的关系式，可整理出更简洁的粉尘层填充率计算式：
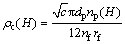(16)
本文的模拟结果(见图5)和文献[31-32]的实验观察结果均已表明粉尘层填充率沿粉尘层厚度方向存在明显变化。因此，这里给出不同Pe下粉尘层填充率的空间分布，以便观察粉尘层的孔隙结构变化特征。由于Pe＜10时粒子的布朗随机运动较强，粒子在计算区域的运动时间显著增加，从而导致计算过程极为耗时。在不影响粉尘层填充率计算结果，经试算，将计算粒子数减少为2 000个以降低计算代价，其余Pe下计算粒子数取为5 000个，计算结果如图8所示。由纤维中心点起量的粉尘层厚度(量纲一的量)定义为粉尘层实际厚度与粒子直径的比值。
由图8可知：Pe对粉尘层填充率及其分布影响显著。对于Pe＞10情形，粉尘层填充率随厚度增加先经历急剧上升的过程，再进入相对平稳的变化阶段，最后填充率随着厚度增加急剧下降。同时也观察到，随着Pe的减小，粉尘层填充率随厚度急剧上升的过程逐渐缩小。当Pe＜10时，粉尘层填充率随厚度急剧上升的关系已演变为与之相反的情形，即随着粉尘层厚度的增加，填充率呈急剧下降的变化趋势，这一结果进一步说明粒子输运机制对粉尘层形态结构的影响。Pe较大时粒子的输运机制由对流作用主导，粒子被纤维捕集过程主要是通过拦截机理来完成。由图4可知：Pe较大时粒子被纤维捕集的效率较低。因此，在纤维表面形成的粉尘树枝数目较少，且单个粉尘树枝中包含的粒子数目亦较少，只有当粉尘树枝生长到一定高度时，单个粉尘树枝中包含的粒子数才表现出明显增加的趋势(见图5(b))。在rc-H的关系曲线上，这一现象表现为粉尘层底层填充率较小，且随粉尘层高度增加而逐渐增大。当粒子的输运机制演变为扩散作用主导时(Pe＜10)，被纤维捕集的粒子数明显增多，甚至在纤维的背风面也出现了粉尘树枝结构(见图5(a))。但由于此条件下受粉尘树枝“非均衡”生长的影响，较大的粉尘树枝有更多的机会接触到来流粒子而继续生长，而相对矮小的树枝则被邻近较大树枝屏蔽而无法接触到来流粒子，从而停止生长，这一过程必将引起粉尘层填充率随厚度增加反而下降。
尽管Pe不同时粉尘层填充率随厚度的细节变化存在差异，但仍可将粉尘层划分为3个典型结构组成。在粉尘层的底层存在一个填充率随高度急剧增大或降低的粉尘层结构，称之为“滤饼基层”，对粉尘层的形成速度和稳定性起关键作用。在滤饼基层上方的粉尘层填充率随厚度的变化相对比较稳定，通常将该层称为“滤饼主体层”，对过滤压降的形成起主要贡献。而将粉尘层表层存在填充率急剧下降的区域称为“滤饼表层”。这里需要指出的是，粉尘层填充率变化区间的划分与粉尘层形成过程中3个阶段的划分属于不同物理问题的描述。滤饼基层是由粒子黏附和粉尘树枝桥接过程形成的粉尘层结构，而滤饼主体层和滤饼表层是滤饼生长过程阶段的结果。
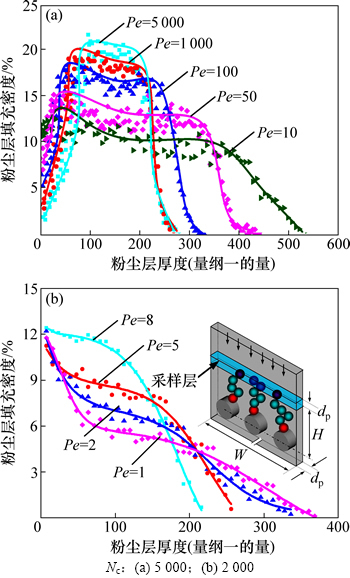
图8 不同Pe下粉尘填充率与粉尘层厚度的关系
Fig. 8 Relationship between packing density and height of dust layer for different Pe
3 结论
1) 当Pe＜1000时，基于离散随机模拟方法求解出的单纤维扩散效率与Rao和Lee的计算结果均具有较好的一致性。当Pe＞1000时，本文计算结果与Rao的结果吻合较好，而略高于Lee的计算值。这表明本文给出的离散随机模拟方法适应于纤维表面气溶胶粒子对流扩散沉积动力学行为的计算。
2) 粉尘层的形态结构主要取决于粒子的输运机制，以扩散输运机制主导的粒子沉积过程将形成更为开放、松散的粉尘层结构。纤维表面粒子沉积行为表现出粉尘黏附、粉尘树枝桥接和滤饼生长3个典型阶段。各个阶段所经历的时间依赖于Pe，在Pe＜10时，粉尘黏附和粉尘树枝桥接2个阶段几乎无法察觉。
3) 所有Pe下的粉尘层填充率随粉尘层厚度均存在3个典型变化区间。在粉尘层的底层存在一个填充率随高度急剧增大或降低的粉尘层结构，即“滤饼基层”。在滤饼基层上方的粉尘层填充率随厚度的变化相对比较稳定，而在粉尘层表层则存在填充率急剧下降的区域。
参考文献：
[1] 周敏, 陈长虹, 乔利平, 等. 2013 年 1 月中国中东部大气重污染期间上海颗粒物的污染特征[J]. 环境科学学报, 2013, 33(11): 3118-3126.
ZHOU Min, CHEN Changhong, QIAO Liping, et al. The chemical characteristics of particulate matters in Shanghai during heavy air pollution episode in Central and Eastern China in January 2013[J]. Acta Scientiae Circumstantiae, 2013, 33(11): 3118-3126.
[2] 赵艳霞, 侯青. 1993—2006 年中国区域酸雨变化特征及成因分析[J]. 气象学报, 2008, 66(6): 1032-1042.
ZHAO Yanxia, HOU Qing. An analysis on spatial/temporal evolution of acid rain in China (1993—2006) and its causes[J]. Acta Meteorologica Sinica, 2008, 66(6): 1032-1042.
[3] 师华定, 高庆先, 张时煌, 等. 空气污染对气候变化影响与反馈的研究评述[J]. 环境科学研究, 2012, 25(9): 974-980.
SHI Huading, GAO Qinxian, ZHANG Shihuang, et al. Research review of impacts and feedback of air pollution on climate change[J]. Research of Environmental Sciences, 2012, 25(9): 974--980.
[4] Thomas D, Penicot P, Contal P, et al. Clogging of fibrous filters by solid aerosol particles experimental and modelling study[J]. Journal of Aerosol Science, 2001, 56(11): 3549-3561.
[5] Song C B, Park H S, Lee K W. Experimental study of filter clogging with monodisperse PSL particles[J]. Powder Technology, 2006, 163(3): 152-159.
[6] Myojo T, Kanaoka C, Emi H. Experimental observation of collection efficiency of a dust-loaded fiber[J]. Journal of aerosol science, 1984, 15(4): 483-489.
[7] Payatakes A C, Gradoń L. Dendritic deposition of aerosols by convective Brownian diffusion for small, intermediate and high particle Knudsen numbers[J]. Journal of American Institute of Chemical Engineers, 1980, 26(3): 443-454.
[8] YANG Mengmeng, LI Shuiqing, YAO Qiang. Mechanistic studies of initial deposition of fine adhesive particles on a fiber using discrete-element methods[J]. Powder Technology, 2013, 248(2): 44-53.
[9] Kasper G, Schollmeier S, Meyer J, et al. The collection efficiency of a particle-loaded single filter fiber[J]. Journal of Aerosol Science, 2009, 40(12): 993-1009.
[10] Kasper G, Schollmeier S, Meyer J. Structure and density of deposits formed on filter fibers by inertial particle deposition and bounce[J]. Journal of Aerosol Science, 2010, 41(12): 1167-1182.
[11] Penicot P, Thomas D, Contal P, et al. Clogging of HEPA fibrous filters by solid and liquid aerosol particles: An experimental study [J]. Filtration & Separation, 1999, 36(2): 59-64.
[12] Calle S, Contal P, Thomas D, et al. Evolutions of efficiency and pressure drop of filter media during clogging and cleaning cycles[J]. Powder Technology, 2002, 128(2): 213-217.
[13] Bourrous S, Bouilloux L, Ouf F X, et al. Measurement of the nanoparticles distribution in flat and pleated filters during clogging[J]. Aerosol Science and Technology, 2014, 48(4): 392-400.
[14] Tanabe E H, Barros P M, Rodrigues K B, et al. Experimental investigation of deposition and removal of particles during gas filtration with various fabric filters[J]. Separation and Purification Technology, 2011, 80(2): 187-195.
[15] Kanaoka C, Hiragi C, Tanthapanichakoon C. Stochastic simulation of the agglomerative deposition process of aerosol particles on an electret fiber[J]. Powder Technology, 2001, 118(1/2): 97-106.
[16] Bang J, Yoon W. Stochastic analysis of a collection process of submicron particles on a single fiber accounting for the changes in flow field due to particle collection[J]. Journal of Mechanical Science and Technology, 2014, 28(9): 3719-3732.
[17] Hosseini S A, Tafreshi H V. Modeling particle-loaded single fiber efficiency and fiber drag using ANSYS-Fluent CFD code[J]. Computers & Fluids, 2012, 66: 157-166.
[18] WANG Haoming, ZHAO Haibo, GUO Zhaoli, et al. Numerical simulation of particle capture process of fibrous filters using Lattice Boltzmann two-phase flow model[J]. Powder Technology, 2012, 227(9): 111-122.
[19] 朱辉, 付海明, 亢燕铭. 纤维表面气溶胶粒子沉积与反弹行为数值模拟[J]. 中南大学学报(自然科学版), 2013, 44(7): 3086-3094.
ZHU Hui, FU Haiming, KANG Yanming. Numerical simulation of particles deposition and rebound on fiber surface[J]. Journal of Central South University (Science and Technology), 2013, 44(7): 3086-3094.
[20] 
W. Simulation of the filtration behaviour of dust filters[J]. Simulation Practice and Theory, 1998, 6(3): 281-296.
[21] Jeon K J, Jung Y W. A simulation study on the compression behavior of dust cakes[J]. Powder Technology, 2004, 141(1): 1-11.
[22] Reist P C. Aerosol science and technology[M]. 2nd ed. New York: McGraw-Hill Press, 1993: 52-65.
[23] Li A, Ahmadi G. Dispersion and deposition of spherical particles from point sources in a turbulent channel flow[J]. Aerosol Science and Technology, 1992, 16(4): 209-226.
[24] Yates J T, Johnson J K. Molecular physical chemistry for engineers[M]. Sausalito: University Science Books Press, 2007: 317-320.
[25] Huang W, Hibbert D B. Fast fractal growth with diffusion, convection and migration by computer simulation: Effects of voltage on probability, morphology and fractal dimension of electrochemical growth in a rectangular cell[J]. Physica A: Statistical Mechanics and its Applications, 1996, 233(3): 888-896.
[26] Huang W, Hibbert D B. Computer modeling of electrochemical growth with convection and migration in a rectangular cell[J]. Physical Review E, 1996, 53(1): 727-730.
[27] Kuwabara S. The forces experienced by randomly distributed parallel circular cylinders or spheres in a viscous flow at small reynolds numbers[J]. Journal of the Physical Society of Japan, 1959, 14(4): 527-532.
[28] Henry F, Ariman T. Cell model of aerosol collection by fibrous filters in an electrostatic field[J]. Journal of Aerosol Science, 1981, 12(2): 91-103.
[29] Lee K W, Liu B Y H. Theoretical study of aerosol filtration by fibrous filters[J]. Aerosol Science and Technology, 1982, 1(2): 147-161.
[30] Rao N, Faghri M. Computer modeling of aerosol filtration by fibrous filters[J]. Aerosol Science and Technology, 1988, 8(2): 133-156.
[31] Chen Y S, Hsiau S S. Cake formation and growth in cake filtration[J]. Powder Technology, 2009, 192(2): 217-224.
[32] Schmidt E. Experimental investigations into the compression of dust cakes deposited on filter media[J]. Filtration & Separation, 1995, 32(8): 789-793.
(编辑 赵俊)
收稿日期：2014-12-10；修回日期：2015-03-14
基金项目(Foundation item)：国家自然科学基金资助项目(51178094)；广西教育厅科研基金资助项目(2013YB275)(Project (51178094) supported by the National Natural Science Foundation of China; Project (2013YB275) supported by the Scientific Research Project of Education Department of Guangxi, China)
通信作者：付海明，博士，高级工程师，从事空气过滤净化与空气品质研究；E-mail：fhm@dhu.edu.cn
