基于方差传递模型的大坝廊道注浆节点定位稳健优化

陈娟¹，徐力生¹，徐蒙¹，张帆²，李凤玲³

(1. 中南大学 地球科学与信息物理学院，湖南 长沙，410083；

2. 中南大学 机电工程学院，湖南 长沙，410083；

3. 长沙理工大学 汽车与机械工程学院，湖南 长沙，410076)

摘要：针对大坝廊道注浆环境复杂造成无线信号传输受各种不确定性噪声因素影响较大等工程实际问题，基于不确定性分析理论中的方差传递模型，提出一种大坝廊道注浆节点定位稳健优化方法。考虑节点定位偏差的波动和噪声因子，采用最小二乘法对已测量的数据拟合得出多项式模型；根据定位偏差的方差、噪声因子的方差与接收信号强度(R_SSI)方差的传递关系，估计R_SSI的均值与方差。以最小化R_SSI的均方差与无线传感网络能量消耗为稳健优化准则，对节点定位进行稳健优化。以实际注浆工程无线信号传输节点铺设为例，采用所提出的方法进行分析并与常规的极大似然估计定位方法进行对比。研究结果表明：与常规方法相比，所提出的方法可有效减少R_SSI均方差的波动，降低信号传输过程中的能量损耗，信号传输更加稳定。

关键词：节点定位；稳健优化；廊道注浆；方差传递

中图分类号：TP212；TV543               文献标志码：A         文章编号：1672-7207(2014)11-3915-07

Robust optimization of nodes localization in dam corridor grouting based on transmitted variance model

CHEN Juan¹, XU Lisheng¹, XU Meng¹, ZHANG Fan², LI Fengling³

(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;

2. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;

3. College of Automobile & Mechanical Engineering, Changsha University of Science & Technology,

Changsha 410076, China)

Abstract: Due to the corridor complex environment of dam grouting, the wireless signal transmission will be influenced by various uncertainty noise factors. Based on the transmitted variance model of uncertainty analysis theory, a robust optimization method was proposed for nodes localization. Considering the nodes positioning deviation fluctuation and noise factors, the least square method was used to fit the polynomial model of measured data. According to the transitive relation between the variance of positioning deviation, the variance of noise factor and the variance of received signal strength indication (R_SSI), the mean value and variance of R_SSI was estimated. Taking the minimization of the mean-square deviation of R_SSI and the energy consumption of wireless sensor network as optimization goals, the robust optimization for the localization of the nodes was realized. The nodes localization process of practical grouting wireless signal transmission was taken as an example to verify the proposed method and compared with the conventional maximum likelihood estimation location method. The results show that the proposed method can effectively reduce the variance fluctuation of R_SSI and the energy consumption during signal transmission, and the signal transmission process is more stable.

Key words: nodes localization; robust optimization; corridor grouting; variance transmission

灌浆廊道施工环境复杂，在各种不确定性噪声因素干扰下，导致无线网络数据传输数据丢包率高、网络稳定性差进而影响廊道中的无线网络通信质量。节点布置是无线传感网络研究的一个热点问题。相关研究表明，在无线网络中，锚节点附近节点由于需要承担较多的数据转发任务而需要消耗更多的能量，容易产生由于能量耗尽而过早失效，使得锚节点周围出现能量空洞，导致整个无线网络瘫痪^[1-2]。任炬等^[3]提出了一种基于代理和环形路由的传感器网络覆盖空洞修复策略，实现了降低网络能耗，提高节点存储容量的目的。周广东等^[4]针对线性无线传感网络的“能量洞”问题，提出了一种基于数据获取效率的大跨桥梁监测无线传感网络节点布置方法。陆克中等^[5]通过分析无线传感器网络中的能量消耗，提出了一种非均匀节点布置方法。石欣等^[6]针对基于信号强度(R_SSI)的无线传感器网络室内移动目标定位算法易受干扰、波动较大等问题，基于粒子群算法，提出了一种改进的信号强度多维标度室内定位算法。崔玮等^[7]针对室内环境中的无线传感器网络节点定位，通过分析定位误差模型，结合高斯混合模型提出了一种无需先验知识的节点定位算法。在狭长区间无线信号传输方面，文献[8-9]对隧道和矿井巷道进行的信号传播特性进行了研究。罗熠等^[10]以IEEE804.15.4为基础，介绍了基于无线传感器网络的灌浆网络监测系统的总体架构及软硬件设计过程。李敬兆等^[11]对应用于开阔环境下的无线感知节点定位算法进行了修正，提出了应用于狭长空间的无线感知节点布置策略与定位算法。目前，基于信号强度(R_SSI)的节点布置算法已有很多研究成果，但都面临着一个共同的问题，即无线信号传输过程中受环境噪声因素的影响很大，且不同环境对应不同的路径损耗模型及参数影响不同。因此，用固定的路径损耗模型来描述信号强度与距离的关系会给节点定位距离的估计带来较大的误差。常规的定位算法一般以固定的损耗模型为基础，对测得的信号强度R_SSI进行筛选或修正，保证信号强度R_SSI的精确度，在一定程度上提高了距离估算的精度，但忽略了噪声因素对距离的严重影响。而稳健优化方法^[12]可以给出对噪声因素不敏感的稳健条件，有效减少质量波动。为此，本文作者基于不确定性分析理论中的方差传递模型，提出一种大坝廊道注浆节点定位稳健优化方法。考虑节点定位偏差的波动和噪声因子，采用最小二乘法对已测量的数据拟合得出多项式模型，根据定位偏差的方差、噪声因子的方差与信号强度方差的传递关系，估计信号强度的均值与方差，并以最小化信号强度的均值与方差为稳健优化准则，对节点定位进行稳健优化。

1  常规定位方法及原理

节点之间的距离由信号强度反映。在众多的无线传感器网络节点算法中，基于信号收发强度的算法更加适合于廊道这样的狭长空间环境^[9]。考虑障碍物干扰以及温度和湿度等参数对信号传播的影响，采用以下路径损耗模型^[13]：

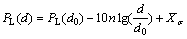       (1)

式中：d₀为参考距离，通常取为1 m；n为衰减指数；X_σ为平均值为s、标准差σ范围在4~10^[13]的高斯噪声变量，σ越大，表示模型的不确定性越大；P_L(d₀)为经过参考距离d₀后接收端信号强度。P_L(d)为距离d时接收端的信号强度R_SSI，

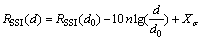      (2)

2  信号传输模型参数估计

由于廊道情况不同，廊道内无线信号传播模型也不同。本文首先测量一组廊道内信号强度(R_SSI)数据，然后用这些数据拟合出节点信号传输模型，用此模型对以后的节点进行定位优化。信号传输模型的多项式拟合可表示为

                (3)

式中：为信号强度R_SSI拟合值；d为信号发射节点与接收节点之间的距离；a_j(j=0, 1, …, k)为模型拟合系数；k为拟合阶次；w为噪声因素，假定其服从均值为s、标准差为σ的正态分布。第i次测量值为(d_i, P_i)，i=1, 2, …, n。

根据拟合得到的函数P_fit(d)与实际P(d)之间的偏差△P=P_fit(d)-P(d)即在d处的残差，确定噪声因素的

均值s与标准差σ。定义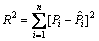为总的估计误差，根据

                  (4)

将式(4)代入式(3)，得正规方程组为

  (5)

定义

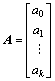；；   (6)

根据最小二乘法的基本原理，拟合系数矩阵A的最优估计为

            (7)

3  基于方差传递模型的稳健定位算法

大坝廊道灌浆施工区域的环境复杂，施工器械、工作人员较集中，温度、湿度、噪声干扰偏高。在信号传播过程中，受到这些障碍物引起的散射、反射、绕射射线的干扰，波动幅度较空旷区域明显变大，常规的定位算法无法考虑这些噪声因素对灌浆无线信号传输的影响。

3.1  方差传递模型

稳健优化是指当设计参数存在一定变差或受各种因素的干扰时，仍然能保证目标稳定的一种工程优化方法^[12]。2001年，Shirley等^[14]提出用方差传递模型进行稳健优化，考虑噪声因子的方差与响应方差的传递关系如下：

       (8)

当接收信号强度(R_SSI)和噪声因子互为统计独立时，将P(d, w)在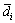和处展开成泰勒级数，可得：

      (9)

    (10)

式中：μ_P为信号强度R_SSI的均值；σ_P为信号强度R_SSI的方差；σ_di为第i个节点距离d_i的方差。

3.2  能量消耗模型

为验证所提出优化算法的有效性，采用经典的能量消耗模型计算不同节点定位方案下传输l bit信息经过距离d所消耗的能量^[15]。

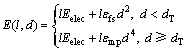       (11)

式中：E_elec为传输或者接收每比特数据所消耗的能量，与电路数字编码、调制、滤波和信号传播情况有关；ε_fs和ε_mp分别为传输距离小于d_T与大于等于d_T时功率放大所消耗的能量，取决于接受器的距离和误码率；d_T为临界距离。

3.3  稳健优化

节点定位稳健优化需要实现2个目标：一是使节点定位估计得距离尽可能接近真实值；二是使R_SSI的波动(以R_SSI的方差表示)尽可能小。本文基于式(9)和(10)采用最小化均方误差作为优化准则对R_SSI的均方误差与节点能量消耗进行优化，以此求出最佳节点铺设距离：

          (12)

式中：f_mse(d)为R_SSI的均方误差。对于式(12)所描述的多目标优化问题，采用理想点法求其Pareto解。根据多项式拟合之后的余量数据，经拟合得到的函数关系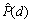与实际P(d)数据间的偏差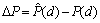，确定噪声因子w的均值与方差。根据方差传递模型，计算R_SSI方差，在R_SSI均方差与网络能量消耗最小的条件下，优化求解节点定位坐标。基于方差传递的节点定位优化算法流程如图1所示。

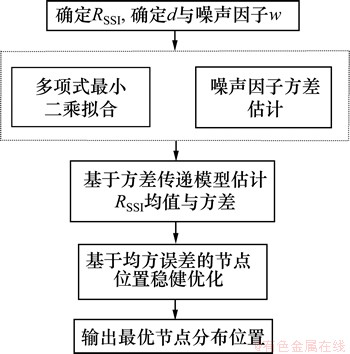
图1  基于方差传递的节点定位优化算法流程图

Fig. 1  Flow chart of node localization algorithm optimization based on variance transmission

3.4  节点坐标的最小二乘估计

设定n个锚节点的坐标为(x_i, y_i)，其中i=1, 2, …, n，待定位节点的坐标为B=[x, y]^T，锚节点到待定位节点的距离分别为d₁, d₂, …, d_n，则有

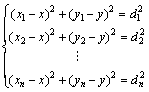           (13)

用向量表示为

BX=C                   (14)

其中：；；。

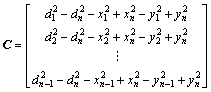使用最小二乘估计未知节点的坐标为

             (15)

式中：表示未知节点坐标的估计值。

3.5  基于信号衰减模型的克拉美-罗界分析

根据式(2)所确定的廊道内信号衰减模型，则第i个节点的接受信号强度P_i的概率密度函数为

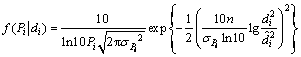    (16)

似然函数为

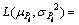
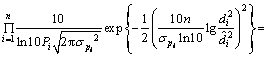
      (17)

式中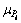：为第i个节点的接收信号强度P_i的均值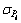；为第i个节点接收信号强度P_i的标准差。

对等式(2)两边求对数得联合概率密度函数为

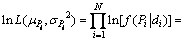
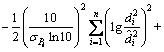
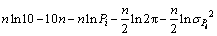      (18)

根据克拉美-罗定理^[16]，节点距离d估计误差的克拉美-罗界为

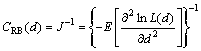      (19)

式中：C_RB(d)表示参数d的克拉美-罗界；矩阵，通常称为Fisher信息矩阵。将式(18)代入式(19)得

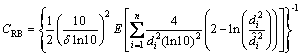    (20)

式中：为未知节点与锚节点之间距离的估计值。

4  实例分析

以云南糯扎渡水电站大坝廊道注浆通信节点铺设为例，运用所提出的节点定位稳健优化算法，对廊道内节点定位进行优化。无线传感器检测系统节点选用CC2430芯片，该芯片是基于ZigBee技术的2.4 GHz射频系统芯片，使用8051微处理器内核，集成无线通信模块，接收信号强度可以从CC2430内置接收信号强度指示器RSSIL.RSSI_VAL读出。廊道分叉区域节点布置示意图如图2所示。已知5个锚节点的分布位置，采用本文所提出的稳健定位优化算法，对未知节点进行位置优化。无线传感网络节点的参数如表1所示。

图2  廊道分叉区域节点布置示意图

Fig. 2  Node layout schematic diagram of corridor bifurcation area

表1  试验区域无线网络参数

Table 1  Wireless network parameters of experimental area

为了更加直观地了解廊道环境对信号的影响，试验在具有分岔结构的廊道内进行，试验廊道宽为5.0 m，高为2.6 m，根据廊道实际结构与现场环境，在节点允许分布范围内连续布置信号强度监测点，测得5个锚节点的R_SSI衰减曲线如图3所示。由图3可以看出：受各种现场条件影响，实际的R_SSI衰减曲线并不是光滑规则的曲线，而是表现为不规则的震荡和衰落；分岔区域中的锚节点3与锚节点5的R_SSI衰减幅度要比平直廊道中的锚节点1，2与4的大。根据测得的锚节点R_SSI衰减数据，拟合得到信号传输模型。

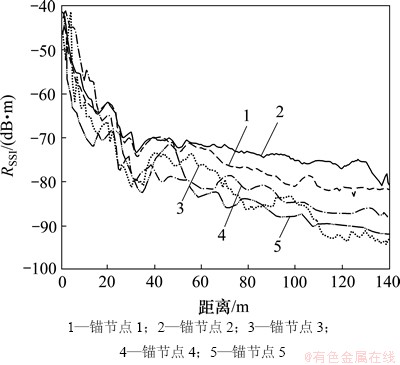
图3  不同锚节点实测R_SSI衰减曲线

Fig. 3  R_SSI measured decay curves of different anchor nodes

图4所示为对于不同的锚节点，采用本文提出的方差传递模型、极大似然估计方法与对数距离路径损耗模型克拉美-罗界对比。从图4可以看出：极大似然估计方法的定位误差的均方差要比本文所提出的稳健定位算法的大，定位误差不稳定，受噪声因素影响较大；位于分岔区域中的锚节点3与锚节点5的定位误差要比平直廊道中的锚节点1，2与4的大。

表2所示为稳健定位优化结果与常规极大似然估计优化结果对比。从表2可知：在5种稳健定位优化节点布置方案下锚节点1~5的R_SSI均值与方差都要比极大似然估计方法的小，方差波动值分别减小了41.59%，56.67%，43.8%，23.74%与43.62%，说明节点在稳健定位方案下，R_SSI波动值受噪声因素影响降低，信号传输更稳定。

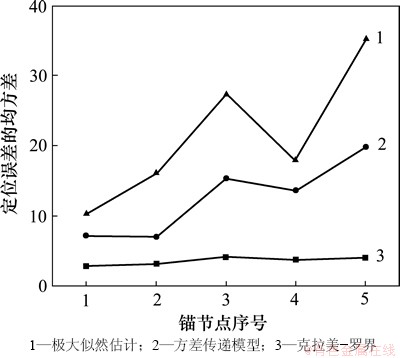
图4  不同锚节点定位误差对比

Fig. 4  Comparison of different anchor node localization error

表2  稳健定位优化结果与常规优化结果对比

Table 2  Comparison of results of robust positioning optimization and conventional optimization

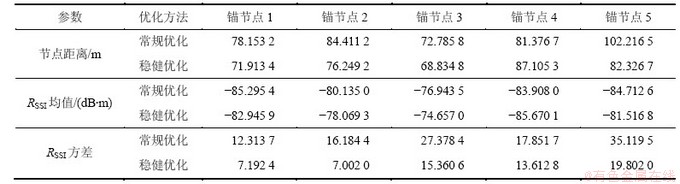
图5所示为采用方差传递模型与极大似然估计方法对未知节点进行定位优化后，锚节点向未知节点发送1 000 bit数据的能量消耗对比。从图5可以看出：与极大似然方法相比，采用方差传递模型优化节点位置后，锚节点向未知节点发送1 000 bit数据消耗的能量总体上降低了8.95%。在廊道灌浆施工过程中，锚节点通常需要连续不断接受与发送实时灌浆参数，数据传输量巨大。采用本文提出的方法能显著降低数据传输的能耗，提高无线传感网络寿命。

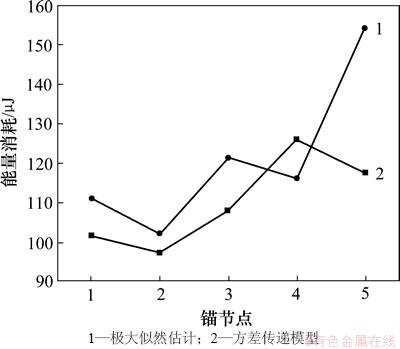
图5 不同定位方案能量消耗对比

Fig. 5 Comparison of energy consumption with different positioning schemes

为了进一步对所提出的节点稳健定位方法进行性能评估，在现场试试丢包率。实验范围为120 m之内的廊道内，灌浆数据采样频率为1 s采集6次数据。

表3  无线信号传输性能分析

Table 3  Analysis of wireless signal transmission performance

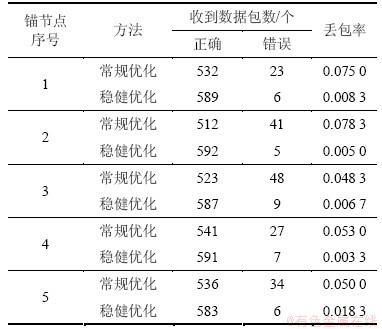
采集的数据参数包括流量、压力、密度、抬动位移，仪器的采样间隔为0.16 s，每次采样的数据帧长度为80~150 Byte，灌浆设备的数据传输速率为2 500 bit/s，节点的数据传输速率250 kbit/s，所得结果见表3。

分析表3可知：在节点稳健优化定位方案下，各锚节点无线信号传输的丢包率均比常规定位方案的低，说明利用所提出的稳健定位优化算法优化节点位置可获得更好的信号传输性能。

5  结论

1) 在稳健定位优化节点布置方案下，信号强度R_SSI均值与方差都要比极大似然估计方法的小，锚节点1~5的R_SSI方差波动值分别减小了41.59%，56.67%，43.80%，23.74%与43.62%，说明节点在稳健定位方案下，R_SSI波动值受噪声因素影响降低。

2) 与极大似然方法相比，采用方差传递模型优化节点位置后，锚节点向未知节点发送1 000 bit数据消耗的能量总体上降低8.95%。

3) 在节点稳健优化定位方案下，各锚节点无线信号传输的丢包率均比常规定位方案的低，说明利用所提出的稳健定位优化算法优化节点位置可获得更好的信号传输性能，信号传输更稳定，能适应廊道分岔等复杂注浆环境的节点定位优化。

参考文献：

[1] 吴小兵, 陈贵海. 无线传感器网络中节点非均匀分布的能量空洞问题[J]. 计算机学报, 2008, 31(2): 253-261.

WU Xiaobing, CHEN Guihai. The energy hole problem of no uniform node distribution in wireless sensor networks[J]. Chinese Journal of Computers, 2008, 31(2): 253-261.

[2] 刘安丰, 聂红伟, 吴贤佑, 等. 基于网络效率的线性无线传感器网络优化部署算法[J]. 计算机科学, 2009, 36(11): 83-87.

LIU Anfeng, NIE Hongwei, WU Xianyou, et al. Optimization deployment algorithm for network efficiency of linear wireless sensor networks[J]. Computer Science, 2009, 36(11): 83-87.

[3] 任炬, 刘安丰, 陈志刚. 一种基于代理和环形路由的传感器网络覆盖空洞修复策略[J]. 中南大学学报(自然科学版), 2014, 45(8):2629-2639.

REN Ju, LIU Anfeng, CHEN Zhigang. An efficient coverage maintenance scheme based on proxy information sharing and circular routing in WSNs[J]. Journal of Central South University (Science and Technology), 2014, 45(8): 2629-2639.

[4] 周广东, 李爱群. 大跨桥梁监测无线传感网络节点布置方法研究[J]. 振动工程学报, 2011, 24(4): 405-411.

ZHOU Guangdong, LI Aiqun. Nodes arrangement method of wireless sensor network on long span bridge monitoring[J]. Journal of Vibration Engineering, 2011, 24(4): 405-411.

[5] 陆克中, 黄刘生, 万颍渝, 等. 无线传感器网络中传感器节点的布置[J]. 小型微型计算机系统, 2006, 27(11): 2003-2006.

LU Kezhong, HUANG Liusheng, WAN Yingyu, et al. Deploying sensor nodes in wireless sensor networks[J]. Journal of Chinese Computer Systems, 2006, 27(11): 2003-2006.

[6] 石欣, 印爱民, 陈曦. 基于 RSSI 的多维标度室内定位算法[J]. 仪器仪表学报, 2014, 35(2): 261-268.

SHI Xin, YIN Aimin, CHEN Xi. RSSI and multidimensional scaling based indoor localization algorithm[J]. Chinese Journal of Scientific Instrument, 2014, 35(2): 261-268.

[7] 崔玮, 吴成东, 张云洲, 等. 基于高斯混合模型的非视距定位算法[J]. 通信学报, 2014, 35(1): 99-106.

CUI Wei, WU Chengdong, ZHANG Yunzhou, et al. GMM-based localization algorithm under NLOS conditions[J]. Journal on Communications, 2014, 35(1): 99-106.

[8] Pallarés F M, Juan F J P, Juan-Llacer L. Analysis of path loss and delay spread at 900 MHz and 2.1 GHz while entering tunnels[J]. Vehicular Technology on IEEE Transactions, 2001, 50(3): 767-776.

[9] 孙继平, 唐亮，陈伟，等. 基于监测覆盖范围的瓦斯传感器无盲区布置[J]. 煤炭学报, 2008, 33(8): 947-950.

SUN Jiping, TANG Liang, CHEN Wei, et al. No-blind-zone placement of methane sensor based on monitoring coverage[J]. Journal of China Coal Society, 2008, 33(8): 947-950.

[10] 罗熠, 于军. 基于无线传感器网络的灌浆参数监测系统[J]. 长江科学院院报, 2010, 27(12): 87-90.

LUO Yi, YU Jun. Grouting monitoring system based on wireless sensor networks[J]. Journal of Yangtze River Scientific Research Institute, 2010, 27(12): 87-90.

[11] 李敬兆, 吴学琴. 狭长空间无线感知节点布置策略及定位算法[J]. 安徽理工大学学报(自然科学版), 2012, 32(4): 6-9.

LI Jingzhao, WU Xueqin. Study on wireless sensor nodes’ layout strategy and localization algorithm in the long and narrow space[J]. Journal of Anhui University of Science and Technology (Natural Science), 2012, 32(4): 6-9.

[12] 陈立周. 稳健设计[M]. 北京: 机械工业出版社, 2000:3-10.

CHEN Lizhou. Robust design[M]. Beijing: China Machinery Press, 2000:3-10.

[13] 朱剑, 赵海, 孙佩刚, 等. 基于RSSI均值的等边三角形定位算法[J]. 东北大学学报(自然科学版), 2007, 28(8): 1094-1097.

ZHU Jian, ZHAO Hai, SUN Peigang, et al. Equilateral triangle localization algorithm based on average RSSI[J]. Journal of Northeastern University (Natural Science), 2007, 28(8): 1094-1097.

[14] Shirley H X, Wu C F J. On the determination of robust settings in parameter design experiments[J]. Statistics & Probability Letters, 2001, 54(2): 137-145.

[15] Heinzelman W B, Chandrakasan A P, Balakrishnan H. An application-specific protocol architecture for wireless microsensor networks[J]. Wireless Communications, IEEE Transactions on, 2002, 1(4): 660-670.

[16] van Trees H L. Optimum array processing Part IV of detection estimation and modulation theory[M]. New York: John Wiley & Sons, 2004: 917-980.

(编辑  陈灿华)

收稿日期：2014-02-25；修回日期：2014-04-21

基金项目(Foundation item)：国家自然科学基金资助项目(51208514，51408069) (Projects(51208514, 51408069) supported by the National Natural Science Foundation of China)

通信作者：徐蒙(1981-)，男，湖南长沙人，博士，讲师，从事灌浆工程仪器仪表方面的教学与研究；电话：18684882476；E-mail: cj8824552@163.com