J. Cent. South Univ. (2018) 25: 3062-3074

DOI: https://doi.org/10.1007/s11771-018-3974-6

Wave propagation control in periodic track structure through local resonance mechanism

WANG Ping(王平)^{1, 2}, YI Qiang(易强)^{1, 2}, ZHAO Cai-you(赵才友)^{1, 2},XING Meng-ting(邢梦婷)^{1, 2}, LU Jun(卢俊)^{1, 2}

1. Key Laboratory of High-speed Railway Engineering of Ministry of Education (Southwest Jiaotong University), Chengdu 610031, China;

2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: Excessive vibration and noise radiation of the track structure can be caused by the operation of high speed trains. Though the track structure is characterized by obvious periodic properties and band gaps, the bandwidth is narrow and the elastic wave attenuation capability within the band gap is weak. In order to effectively control the vibration and noise of track structure, the local resonance mechanism is introduced to broaden the band gap and realize wave propagation control. The locally resonant units are attached periodically on the rail, forming a new locally resonant phononic crystal structure. Then the tuning of the elastic wave band gaps of track structure is discussed, and the formation mechanism of the band gap is explicated. The research results show that a new wide and adjustable locally resonant band gap is formed after the resonant units are introduced. The phenomenon of coupling and transition can be observed between the new locally resonant band gap and the original band gap of the periodic track structure with the band gap width reaching the maximum at the coupling position. The broader band gap can be applied for vibration and noise reduction in high speed railway track structure.

Key words: wave propagation control; periodic track structure; band gap; local resonance mechanism; transfer matrix

Cite this article as: WANG Ping, YI Qiang, ZHAO Cai-you, XING Meng-ting, LU Jun. Wave propagation control in periodic track structure through local resonance mechanism [J]. Journal of Central South University, 2018, 25(12): 3062–3074. DOI: https://doi.org/10.1007/s11771-018-3974-6.

1 Introduction

The straight sections of high speed railway track structure exhibit obvious periodic characteristics, and numerous research findings have shown that the propagation of elastic wave exhibits band gap characteristics in periodic structures. Elastic waves cannot propagate freely in periodic structure within certain frequency ranges, and show significant attenuation properties, which are called band gaps. KUSHWAHA et al [1] put forward the concept of the phononic crystal, which was defined as a new material or structure arranged and formed periodically according to a specially designed artificial structural unit. The band gap characteristics of phononic crystals have attracted much attention and provided new research ideas for conventional periodic structures. Two band gap mechanisms for phononic crystals have been proposed [2]: the Bragg scattering mechanism and the local resonance mechanism. Regarding the Bragg scattering mechanism, the lowest Bragg band gap frequency is closely related to the lattice constant of the periodic structure, therefore it is hard to obtain low frequency band gaps for periodic structures with small unit size. LIU et al [3] proposed the local resonance mechanism in 2000, by which low frequency band gaps could be obtained and successfully control the low frequency vibration in the structure with small unit size. The local resonance mechanism breaks through the limitations of the Bragg band gap and can be implemented as a new research method in the application of low frequency vibration and noise control.

The band gap characteristics of periodic structure, especially the local resonance mechanism, have the potential to realize low frequency band gaps, injecting new vitality into the study of structural elastic wave control [4]. Wave propagation in beams or plates with multiple periodic arrays of attached spring-mass resonators was studied by XIAO et al [5–8]. Under special conditions, when the locally resonant band gap is close to the Bragg band gap, a pseudo ultra-wide band gap is formed and can be applied for vibration reduction in a wide frequency range. CASADEI et al [9] introduced acoustic metamaterials available in fluids by attaching airfoil-like locally resonant units periodically to a uniform beam and analyzed the influence of key factors such as ambient fluid velocity and structure size on the attenuation of flexural waves considering fluid-solid coupling. LI et al [10] studied the effects of parameters on the band gap behaviors of a piping system with Helmholtz resonators and found that Bragg band gaps and locally resonant band gaps are coupled under special conditions, forming ultra-wide coupled band gaps that were helpful for controlling low frequency noise in the pipeline system. Based on the local resonance mechanism, researchers have studied the wave propagation control in structures, including beams [11, 12], rods [13], plates [14, 15], and analyzed the generation mechanisms [16] and variation laws [17, 18] of band gaps in detail. However, for high speed railway track structure, few studies on the control of elastic waves based on the band gap theory have been reported.

In order to reduce the rail vibration and noise radiation caused by the operation of trains, restraining dampers [19] and dynamic vibration absorbers [20, 21] are always adopted. The former mainly involves damping material and a restraint layer on both sides of the rail web, dissipating vibration energy due to the internal friction and mutual slippage of the damping material [22]. According to the experimental results, the overall A-weighted sound pressure level within the carriage decreases by about 8 dB on a particular curve section after the use of rail dampers [23]. The latter concerns a subsystem (vibration absorber) with a natural frequency coincident with the significant vibration frequency of the rail; thus, the vibration can be “absorbed” by the vibration absorber at this frequency. The rail dynamic vibration absorbers can effectively reduce the rail vibration and noise radiation, existing study shows that the vibration absorbers reduce the rail vibration by about 10 dB and the noise level by 3.5 dB [24]. Dynamic vibration absorbers have been widely used for track structure, considering the periodicity of the track structure, the local resonance mechanism concept is already involved in this method. However, structural vibration and noise are usually attributed to the elastic wave propagation in the structure as well as the mutual coupling between the elastic wave and ambient media [25]. Most of the existing studies on dynamic vibration absorbers focus on the vibration while do not deal with the periodic structure and elastic wave band gaps. In this work, the local resonance mechanism is introduced to achieve the wave propagation control in infinite periodic track structure and promote vibration and noise reduction in high speed railways.

2 Theoretical model

The ballastless track structure is widely used for high speed railways in China, and the track structure can be regarded as a periodic structure in which the rail is fastened on the rigid foundation periodically by elastic fastening due to the high substructure stiffness [26]. In order to achieve the low frequency vibration and noise control of the track structure, the local resonance mechanism is introduced, and resonant units are attached periodically in the middle span of the rail to form a locally resonant phononic crystal structure. The local resonators are set symmetrically at both sides of the rail, and consist of elastic layer and mass block, as shown in Figures 1(a)–(c). The vibration of the periodic track structure induced by the moving vehicle is dominant by the vertical direction [27]. In order to study the vertical flexural wave motion in periodic track structure, the simplified physical model is shown in Figure 1(d), in which the rail and fastening system are described with the beam and spring (stiffness is k_r), respectively. Because the resonators at both sides of the rail have the same stiffness and mass and the resonators are consolidated by clampers, thus the locally resonator in a basic unit is described with a simple spring– mass system, in which the vertical stiffness of the elastic layer is k_l and the resonator mass is m_l.

The motion equation of the local resonators can be expressed as:

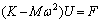                         (1)

where K and M are the stiffness matrix and mass matrix of the local resonators, respectively, ω is the angular frequency; U and F are the displacement vector and force vector, respectively, which can be expressed as:

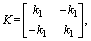
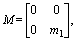
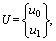
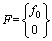 (2)

where k_l is the elastic layer stiffness of the local resonators; m_l is the mass of the local resonators; u₀ is the displacement of the rail; u₁ is the resonator displacement; f₀ is the interaction force between the resonator and rail. Therefore, the following relation can be obtained:

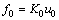                               (3)

where K₀ is the dynamic stiffness of the local resonator: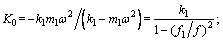f_l is the natural frequency of the local resonator and f=ω/2π.

A Timoshenko beam is used for describing the rail of the track structure, and therefore the wave equation for the free rail can be expressed as [28]:

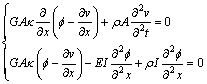           (4)

where G is the shear modulus; A is the sectional area; κ is the shear factor; E is the elastic modulus; I is the sectional inertia moment; ρ is the density of the rail; v is the vertical displacement; f is the bending angle of the rail. The free waves can be calculated according to:

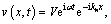
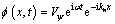        (5)

where V is the vertical displacement amplitude; V_ψ is the angle of rotation of the cross-section; k_n is the wavenumber of the free rail. The ratio relation between bending angle and displacement can be expressed as:

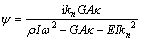                    (6)

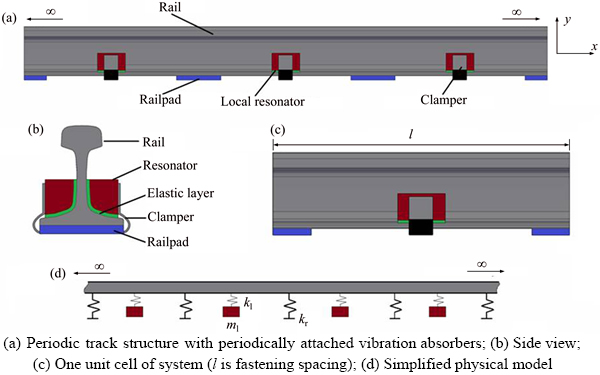
Figure 1 Infinite periodic track structure with local resonators:

At this time, there are two pairs of wavenumbers inverse to each other for the flexural wave, so the displacement response can be expressed as [29]:

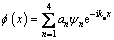         (7)

The state vector of the rail can be expressed as 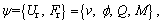where U_r is the displacement vector, including the vertical displacement v and rotational angle f; F_r is the force vector, including the shear force Q and bending moment M. Then the transfer matrix between adjacent periodic units can be obtained:

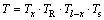                         (8)

where T_x is the state vector transfer matrix with the wave propagation distance x; T_R is the state vector transfer matrix when a wave is transmitted through the local resonators; T_s is the state vector transfer matrix when a wave is transmitted through the fastening:

,

,

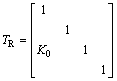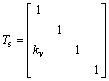                        (9)

In above matrices, k_v is the dynamic stiffness of the fastening; E_n is the state vector factor:

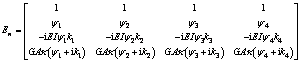 (10)

According to Bloch theorem, the eigenvalue equation for elastic wave propagation in a periodic track structure can be expressed as:

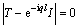                           (11)

where q is the wavenumber of a flexural wave propagating along the periodic track structure, which is also called the Bloch wavenumber. The real part of wavenumber refers to the phase variation, while the imaginary part refers to the damping of the elastic wave, representing the propagation attenuation coefficient. The relation between the wavenumber q and frequency f, i.e. the dispersion characteristics, can be obtained by solving Eq.(11).

3 Flexural wave propagation in locally resonant track structure

Table 1 lists the parameters of the track structure.

Table 1 Track structure parameters [29]

The flexural wave dispersion curve for periodic track structure without local resonators is shown in Figure 2. Since the rail is described with a Timoshenko beam, there are two pairs of characteristic waves inverse to each other. The real part of the Bloch wavenumber indicates the change of the phase, while the imaginary part indicates the attenuation of the propagation of the elastic wave. The elastic wave in the periodic structure can be divided into three regions according to the Bloch wavenumber [8]: 1) Attenuation region (referred to as A); 2) Propagation region (referred to as P); 3) Complex region (referred to as C). According to the formation mechanisms, the band gaps can be divided into two types [17, 18]: 1) the Bragg band gap (BG), in which the Bloch wave vector satisfies Re(ql)=0 or ±π, and Im(ql)≠0; 2) and the local resonant (LR) band gap, in which the Bloch wave vector satisfies Re(ql) ≠0,–π≤Re(ql)≤π.

As shown in Figure 2, within the frequency range below 1500 Hz, the flexural waves in the periodic track structure have two band gaps, which are 0–129 Hz and 1013–1028 Hz, respectively. The first band gap is called foundation band gap, while the second is generated due to Bragg scattering [25]. Though the elastic wave propagation within the band gap can be suppressed, it can be concluded from the complex band structure of the track structure that the bandwidth of the first band gap is narrow and the second band gap is extremely narrow with a weak attenuation. Therefore, the elastic waves can propagate freely within a wide frequency range in the track structure, causing excessive vibration and noise.

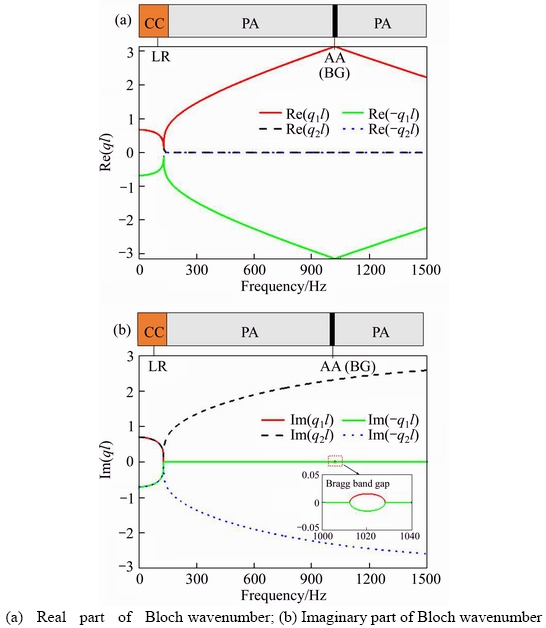
Figure 2 Complex band structure of periodic track without local resonators:

The local resonators are consequently introduced, the resonator mass m_l is 10 kg and the stiffness of the elastic layer k_l is 2×10⁸ N/m. The dispersion curves for the flexural wave of the track structure after the local resonators are installed can be obtained, see Figure 3. The new locally resonant band gap is generated and consists of two regions: AA and CC. The band gap is generated by the periodic resonators, so the two regions can be expressed by a locally resonant (LR) band gap [8]. The band gap range is 599–781 Hz, where the attenuation characteristics are rather obvious. After the local resonators are introduced, they can also influence the original band gaps of the periodic track structure, especially the Bragg band gap, the band gap width and attenuation capability are greatly enhanced. As a result, the propagation of flexural waves in the rail can be suppressed within a wider frequency range, and the band gaps can be tuned according to the vibration and noise control requirements for the track structure.

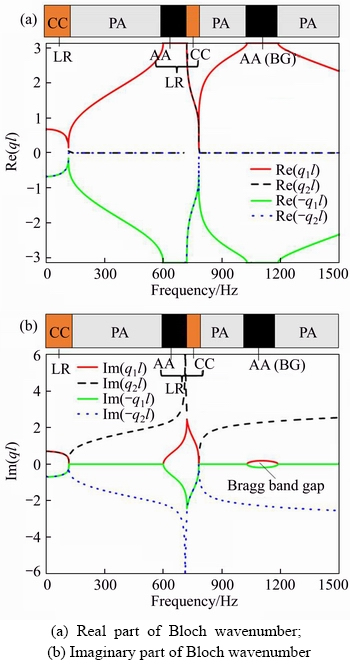
Figure 3 Complex band structure of periodic track with local resonators:

In order to verify the correctness of the theoretical calculation, a finite element model of a 100 m periodic track structure with local resonators is established, and a harmonic excitation load is exerted in the middle of the track. According to the rail responses at 5 spans and 10 spans away from the excitation location, the vibration transmission function can be obtained, see Figure 4. As shown, the transmission attenuation regions coincide with the theoretical results, verifying the correctness of the theoretical model.

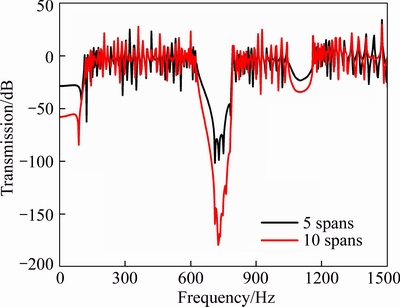
Figure 4 Transmission function of finite track structure with local resonators

4 Band gap tuning of flexural wave

In order to effectively control the vibration and noise of ballastless track structure, the locally resonant mechanism has been adopted to form a novel phononic crystal track structure. The relevant studies show that the vibration and noise from ballastless track structures are mainly located within 500–2000 Hz [27]. If the elastic wave band gap is covered within this frequency range, the vibration and noise radiating from the track structure can be effectively suppressed.

4.1 Local resonator stiffness

In order to broaden the band gap width, the local resonator stiffness is discussed firstly. The mass of the local resonator is constant (m_l=10 kg) and the local resonators are installed in the middle span of the rail at present. Band gap behavior tuned by local resonator stiffness is shown in Figure 5(a). The min|Im(q)| indicates the propagation attenuation characteristics of the flexural wave, thus the color areas in the figure indicate the band gaps. The Timoshenko beam can be used to describe the wave characteristics of the rail below 1500 Hz [29], however, in order to show the coupling between the 2nd order Bragg band gap and the locally resonant band gap, the analysis frequency has been set to 4000 Hz in this section. In low frequency range, two locally resonant band gaps interact with each other and are always subject to a “repulsion” phenomenon. When the stiffness increases, they gradually separate from each other, as shown in Figure 5(b). When the locally resonant band gap approaches the Bragg band gap of the track structure, the locally resonant band gap couples with the Bragg band gap, forming a pseudo ultra-wide band gap under the Bragg conditions, as shown in Figures 5(c) and (d). However, the two band gaps do not coincide with each other since a narrow pass band always exists. In addition, the band gap transition takes place near the coupling. The band gap transition conditions are shown with the red dashed line and coupling conditions are shown with the black dashed line.

It should be noted that after the locally resonant band gap is introduced, the bandwidth of the 1st order Bragg gap decreases first and then increases as the local resonator stiffness increases, while the cut-off frequency stays constant, as shown in Figure 5(c). When k_l=2.35×10⁷ N/m, the starting frequency is equal to the cut-off frequency and the 1st order Bragg band gap will vanish, but the 2nd order Bragg band gap will still be present, see Figure 6. This is because there are two types of modes satisfying the Bragg scattering conditions for periodic track structure, which corresponds to the starting frequency and cut-off frequency of the Bragg band gap, respectively [26]. The local resonators attached in the middle will not influence the cut-off frequency before the band gap coupling. However, the starting frequency increases with a higher local resonator stiffness, and a transition between the starting frequency and cut-off frequency will occur at k_l=2.35×10⁷ N/m. It can be predicted that if the resonator mass is infinite and the stiffness satisfies k_l=k_v (k_v is the vertical stiffness of fastening), the 1st order Bragg band gap will also vanish. The resonator is equivalent to an elastic support at this time, forming a new periodic structure with a lattice constant l/2.

When band gap coupling occurs, the pass band width between the Bragg and locally resonant band gaps reaches the minimum and the Bloch wavenumber satisfies that the frequencies equal the Bragg frequency when Re(ql)=0 and π (see Figures 7 and 8). While the band gaps transition occurs, the complex region (CC region) will vanish, and the band gaps appear to be highly symmetric, see Figure 9(b). During the interaction between two different types of band gaps, the cut-off frequency of the locally resonant band gap will not satisfy Re(ql)=0 or ±π, but will change with the stiffness according to the red points shown in Figure 7, and a PP type pass band will be formed between the locally resonant gap and Bragg band gap. At this time, the band gap transition satisfies the criterion proposed in Ref. [16]: 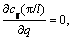or 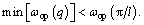According to the band gap coupling and transition process shown in Figure 7,between band gap coupling and transition, both the starting frequency and cut-off frequency of the pass band are not equal to the Bragg frequency, therefore the Bragg frequencies shown in Figures 5(c) and (d) are discontinuous.

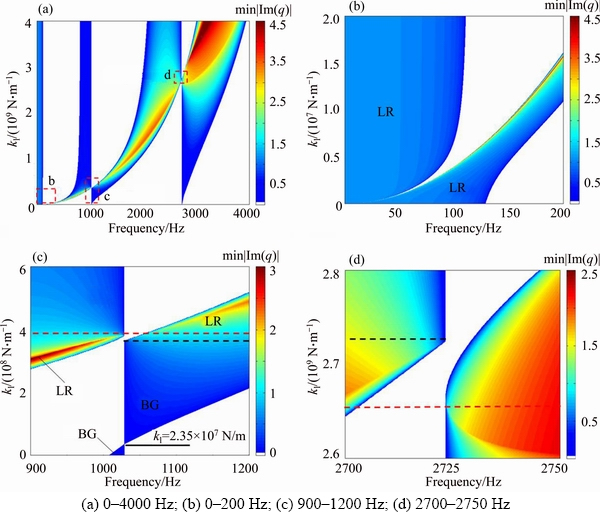
Figure 5 Effects of local resonator stiffness k_l on band gap behavior of locally resonant track structure in different frequency regions:

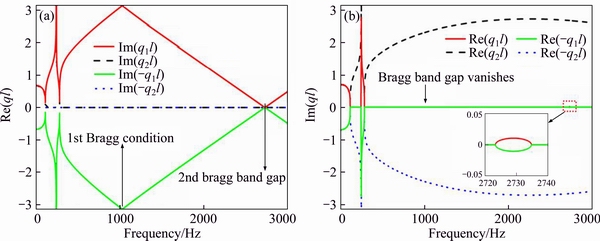
Figure 6 Phenomenon of first Bragg band gap vanishing when k_l=2.35×10⁷ N/m

Meanwhile, when the local resonator mass is constant, the evolution of band gaps based on the natural frequency of the local resonator can also be obtained by adjusting the stiffness, as shown in Figure 10. The natural frequency of local resonators is not always within band gaps. For example, within 1028–1200 Hz, the natural frequency of local resonator is located within the range of the pass band, and the maximum attenuation within band gaps does not coincide with the natural frequency of the resonators. For the approximate coupling conditions, the natural frequency of local resonators is close but not equal to the Bragg frequency.

Figure 7 Real part of band structure in second pass band with increasing stiffness of locally resonators

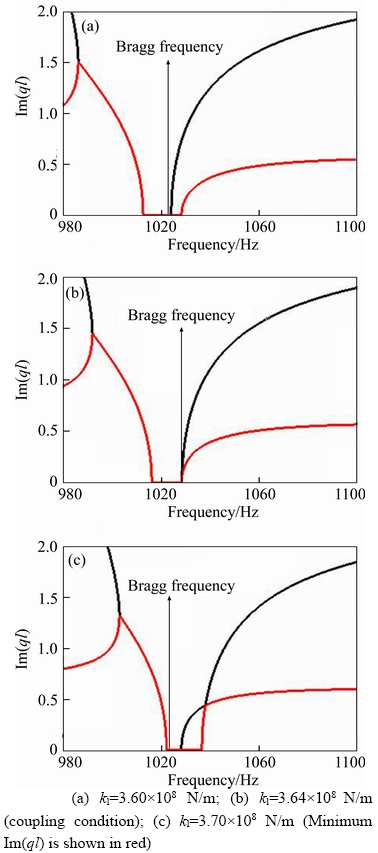
Figure 8 Band gap coupling by tuning local resonator stiffness:

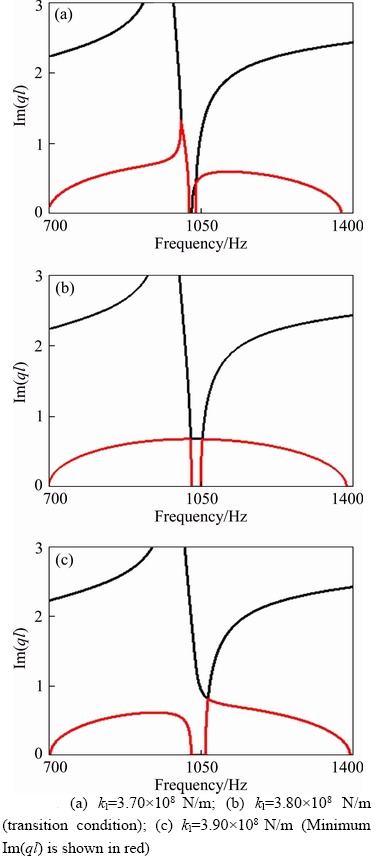
Figure 9 Band gap transition by tuning local resonator stiffness:

4.2 Mass of local resonator

Figure 11 shows the band gap tuning laws based on the local resonator mass when the elastic layer stiffness of the local resonators is selected as k_l=3.8×10⁸ N/m. Along with the increase of the mass, the locally resonant band gap moves to the low frequency range. Near the Bragg frequency, coupling and transition occur between the two types of band gaps. Figures 11(c) and (d) also show the band gap tuned by the natural frequency of the resonator based on the local resonator mass. As the mass decreases, the locally resonant band gap moves to the high frequency range, however the maximum attenuation value within the band gap does not correspond to the natural frequency of the local resonator.

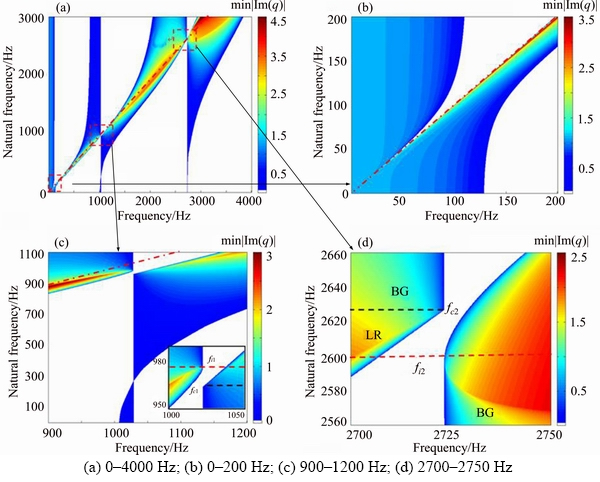
Figure 10 Effects of local resonator natural frequency f_l (with constant mass) on band gap behavior of locally resonant track structure in different frequency regions:

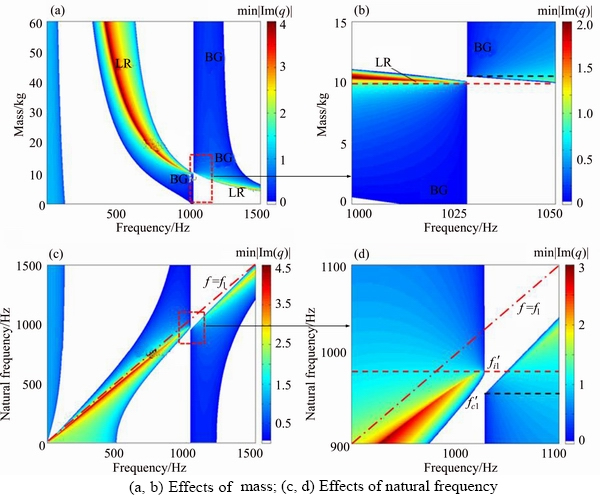
Figure 11 Effects of local resonator mass m_l on band gap behavior of locally resonant track structure:

When the natural frequency of the local resonator is set as f=956.5 Hz (coinciding with the band gap coupling condition in Figure 11), the evolution of the band gap tuned by the local resonator mass can be obtained, as shown in Figure 12. As the local resonator mass increases, the width of the 2nd order band gap gradually increases, while the width of the 3rd order band gap vanishes at m_l=0.15 kg, which has been explicated previously.

4.3 Local resonator position

For the given parameters of the track structure and local resonator, the band gaps can be tuned by adjusting the installation position of the resonators, see Figure 13. The position of the local resonator does not influence the 1st order band gap, because the mode corresponding to the cut-off frequency of the 1st order band gap is the rail-resonator in-phase motion, which is independent of the position of the local resonator in a unit-cell. When local resonator moves to the middle of span, the width of the 2nd order band gap reaches the maximum, while the 3rd order band gap reaches the minimum. The attenuation capability within the band gap will reach the maximum with local resonators installed in the middle span of the rail, thus the propagation of elastic waves can be further controlled.

5 Band gap formation mechanism of locally resonant track structure

According to Mead’s research findings on general one-dimensional periodic multi-coupled systems [30], if the unit-cell of a periodic structure is symmetric, the edge frequency of its band gap will coincide with the free vibration natural frequency of a single unit-cell. When local resonators are installed on the middle span, a basic unit of the periodic structure is shown in Figure 14(a). Both ends of the basic unit are set with an elastic support and a mass-spring system is attached in the middle. In order to simplify the boundary conditions, the elastic supports are described with another set of local resonators [26], however the local resonator mass is infinite, see Figure 14(b). Unit-cell models under the sliding-sliding support boundary condition and pinned- pinned support boundary condition can be established, as shown in Figures 14(c) and (d).

Figure 12 Effects of local resonator mass m_l (with constant natural frequency f_l) on the band gap behavior of locally resonant track structure:

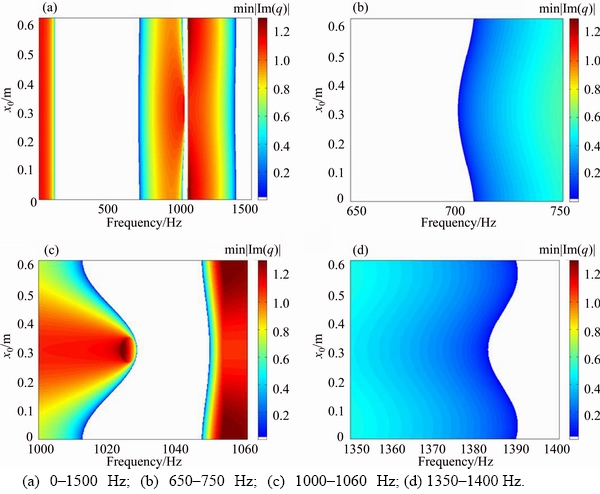
Figure 13 Effects of local resonator position x₀ (with constant parameters of resonators) on band gap behavior of locally resonant track structure in different frequency regions:

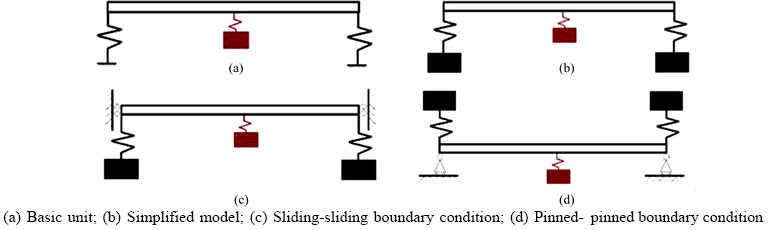
Figure 14 Unit-cell models:

Combing with the finite element model of the periodic track structure, the eigenmodes located at the boundary of the band-gaps can be obtained. For the sliding-sliding boundary condition, symmetric vibration modes include in-phase and anti-phase vibration of the rail and local resonators, as shown in Figures 15(a) and (b). In addition, there is an antisymmetric mode, as shown in Figure 15(c), in which the local resonators do not participate in the vibration. For the pinned-pinned support condition, vibration modes of this model contain the in-phase and anti-phase vibration of the rail and resonator, see Figures 15(d) and (e). These five vibration modes correspond to the starting and cut-off frequencies of the first three order band gaps (the starting frequency of the 1st order band gap is 0). The band edge modes of different types of band gaps can be obtained depending on the vibration modes of a single unit-cell with different boundary conditions.

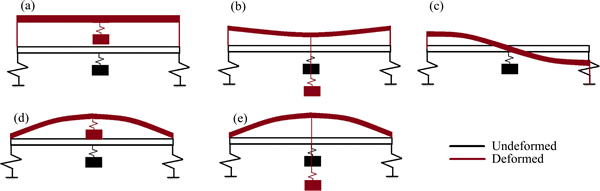
Figure 15 Wave modes of bounding frequencies

6 Conclusions

1) High speed railway track structure possesses obvious periodic characteristic, however, the band gap width is narrow, and the elastic wave attenuation capability is weak. Therefore, it is hard to attenuate the elastic wave propagation in the track structure and excessive vibration and noise radiation can be caused.

2) After the local resonators are installed, the locally resonant band gap is introduced, thus the propagation of flexural wave in the track structure can be further controlled. Meanwhile, the local resonators can also broaden the neighboring Bragg band gap and enhance the attenuation capability of the elastic wave in the band gaps.

3) When the locally resonant band gap is tuned close to the Bragg band gap, coupling and transition occur, a pseudo ultra-wide band gap is formed during coupling, however, the two band gaps will not overlap with each other since a narrow pass band always exists.

4) When local resonators are installed in the middle span of the rail, the symmetric unit-cell models under different boundary conditions can be used to describe the wave modes at the edge of the band gaps.

References

[1] KUSHWAHA M S, HALEVI P, DOBRZYNSKI L. Acoustic band structure of periodic elastic composites [J]. International Journal of Modern Physics B, 1993, 71(13): 2022–2025.

[2] DEYMIER P A. Acoustic metamaterials and phononic crystals [M]. Berlin, Heidelberg: Springer, 2013: 201–215.

[3] LIU Zheng-you, ZHANG Xi-xiang, MAO Yi-wei. Locally resonant sonic materials [J]. Science, 2000, 289(5485): 1734–1736.

[4] ZHENG Ling, LI Yi-nong, BAZ A. Attenuation of wave propagation in a novel periodic structure [J]. Journal of Central South University of Technology, 2011, 18(2): 438–443.

[5] XIAO Yong, WEN Ji-hong, WEN Xi-sen. Broadband locally resonant beams containing multiple periodic arrays of attached resonators [J]. Physics Letters A, 2012, 376(16): 1384–1390.

[6] XIAO Yong, WEN Ji-hong, WEN Xi-sen. Sound transmission loss of metamaterial-based thin plates with multiple subwavelength arrays of attached resonators [J]. Journal of Sound & Vibration, 2012, 331(25): 5408–5423.

[7] XIAO Yong, WEN Ji-hong, HUANG Ling-zhi. Analysis and experimental realization of locally resonant phononic plates carrying a periodic array of beam-like resonators [J]. Journal of Physics D–Applied Physics, 2014, 47(4): 045307.

[8] XIAO Yong, WEN Ji-hong, YU Dian-long. Flexural wave propagation in beams with periodically attached vibration absorbers: Band-gap behavior and band formation mechanisms [J]. Journal of Sound & Vibration, 2013, 332(4): 867–893.

[9] CASADEI F, BERTOLDI K. Wave propagation in beams with periodic arrays of airfoil-shaped resonating units [J]. Journal of Sound & Vibration, 2014, 333(24): 6532–6547.

[10] LI Yan-fei, SHEN Hui-jie, ZHANG Lin-ke, SU Yong-sheng. Control of low-frequency noise for piping systems via the design of coupled band gap of acoustic metamaterials [J]. Physics Letters A, 2016, 380(29, 30): 2322–2328.

[11] PAI F, PENG H, JIANG S. Acoustic metamaterial beams based on multi-frequency vibration absorbers [J]. International Journal of Mechanical Sciences, 2014, 79(1): 195–205.

[12] SHARMA B, SUN C T. Local resonance and Bragg bandgaps in sandwich beams containing periodically inserted resonators [J]. Journal of Sound & Vibration, 2016, 364(22): 133–146.

[13] XIAO Yong, WEN Ji-hong, WEN Xi-sen. Longitudinal wave band gaps in metamaterial-based elastic rods containing multi-degree-of-freedom resonators [J]. New Journal of Physics, 2012, 14(3): 33042.

[14] CLAEYS C C, VERGOTE K, SAS P. On the potential of tuned resonators to obtain low-frequency vibrational stop bands in periodic panels [J]. Journal of Sound & Vibration, 2013, 332(6): 1418–1436.

[15] QIAN Deng-hui, SHI Zhi-yu. Bandgap properties in locally resonant phononic crystal double panel structures with periodically attached spring-mass resonators [J]. Physics Letters A, 2016, 380(41): 3319–3325.

[16] LIU L, HUSSEIN M I. Wave motion in periodic flexural beams and characterization of the transition between Bragg scattering and local resonance [J]. Journal of Applied Mechanics, 2012, 79(1): 011003.

[17] WANG M Y, WANG Xiao-ming. Frequency band structure of locally resonant periodic flexural beams suspended with force–moment resonators [J]. Journal of Physics D–Applied Physics, 2013, 46(25): 255502.

[18] WANG Xiao-ming, WANG M Y. An analysis of flexural wave band gaps of locally resonant beams with continuum beam resonators [J]. Meccanica, 2016, 51(1): 171–178.

[19] ZHAO Cai-you, WANG Ping. Analysis and design of a novel low-noise rail [J]. Journal of Rail & Rapid Transit, 2015, 231(1): 75–89.

[20] WU T X. On the railway track dynamics with rail vibration absorber for noise reduction [J]. Journal of Sound & Vibration, 2008, 309(3): 739–755.

[21] MARZBANRAD J, SHAHSAVAR M, BEYRANVAND B. Analysis of force and energy density transferred to barrier in a single degree of freedom vibro-impact system[J]. Journal of Central South University, 2017, 24(6): 1351–1359.

[22] KIM Y M, YOU K P, YOU J Y. Passive control of along-wind response of tall building [J]. Journal of Central South University, 2014, 21(10): 4002–4006.

[23] ZHAO Cai-you, WANG Ping, YI Qiang. Internal noise reduction in railway vehicles by means of rail grinding and rail dampers [J]. Noise Control Engineering Journal, 2017, 65(1): 1–13.

[24] WILSON Ho, BANTING W. Tuned mass damper for rail noise control [C]// Nagayama: 10th International Workshop on Railway Noise, 2012: 89–96.

[25] NORTON M P, KARCZUB D G. Fundamentals of noise and vibration analysis for engineers [M]. Cambridge: Cambridge University Press, 2003.

[26] WANG Ping, YI Qiang, ZHAO Cai-you. Wave propagation in periodic track structures: band-gap behaviors and formation mechanisms [J]. Archive of Applied Mechanics, 2017, 87(3): 503–519.

[27] LIU H P, WU T X. The influences on railway rolling noise of a rail vibration absorber and wave reflections due to multiple wheels [J]. Journal of Rail & Rapid Transit, 2010, 224(3): 227–235.

[28] PENG Li-ping, JI Ai-min, ZHAO Yue-min, LIU Chu-sheng. Natural frequencies analysis of a composite beam consisting of Euler-Bernoulli and Timoshenko beam segments alternately [J]. Journal of Central South University, 2017, 24(3): 625–636.

[29] THOMPSON D. Railway noise and vibration: mechanisms, modelling and means of control [M]. Oxford: Elsevier Science & Technology, 2009.

[30] MEAD D J. Wave propagation and natural modes in periodic systems: II. Multi-coupled systems, with and without damping [J]. Journal of Sound & Vibration, 1975, 40(1): 19–39.

(Edited by FANG Jing-hua)

中文导读

基于局域共振机理的周期性轨道结构弹性波控制

摘要：高速列车运营过程中轨道结构能够产生剧烈的振动并向外界辐射噪声。虽然轨道结构呈明显周期特征并具有带隙特性，但其带隙范围小，带隙内弹性波衰减能力弱。为了有效抑制轨道结构振动噪声，引入局域共振机理拓宽轨道结构的带隙范围，实现轨道结构中弹性波控制。在钢轨上周期性附加局域共振单元，构成新的局域共振型声子晶体结构，然后分析局域共振单元对弹性波带隙的调控规律，并阐明带隙的形成机理。研究结果表明，引入局域共振单元后，轨道结构产生新的局域共振带隙，该带隙较宽且频率范围可调；局域共振带隙与周期性轨道结构原有带隙产生耦合和转化，并在带隙耦合条件下实现带隙宽度最大化，拓宽后的带隙可用于高速铁路轨道结构振动噪声控制。

关键词：弹性波控制；周期性轨道结构；带隙；局域共振机理；传递矩阵

Foundation item: Project(2016YFE0205200) supported by the National Key Research and Development Program of China; Projects(51425804, 51508479) supported by the National Natural Science Foundation of China; Project(2016310019) supported by the Doctorial Innovation Fund of Southwest Jiaotong University, China; Project(2017GZ0373) supported by the Research Fund for Key Research and Development Projects in Sichuan Province, China

Received date: 2017-12-26; Accepted date: 2018-06-19

Corresponding author: ZHAO Cai-you, PhD, Associate Professor; Tel: +86-15902893274; E-mail: yqzjswjtu2016@163.com; ORCID: 0000-0003-0896-8852