圆弧夹层破坏机制与被动土压力的非线性极限分析

罗卫华

(湖南省高速公路管理局，湖南 长沙，410001)

摘要：在非线性破坏准则下，将水平地震力作为拟静态力，根据极限分析上限定理，利用圆弧夹层破坏机制求解非线性破坏准则下的被动土压力，并将计算结果与多三角形刚块破坏机制下的数值结果进行比较。研究结果表明：圆弧夹层机制下的被动土压力与多三角形刚块机制下的被动土压力几乎相等；水平地震系数与非线性参数对被动土压力有较大影响；土体非线性参数影响破坏面的形状。

关键词：非线性破坏准则；圆弧夹层破坏机制；地震作用；极限分析；被动土压力

中图分类号：TU432          文献标志码：A         文章编号：1672-7207(2011)07-2132-06

Arc-sandwich failure mechanism and passive earth pressure calculation considering nonlinear failure criterion

LUO Wei-hua

(Hunan Expressway Administration Bureau, Changsha 410001, China)

Abstract: Under the condition of nonlinear failure criterion, the earthquake force was regarded as pseudo-static load. In the framework of the upper bound of limit analysis, the passive earth pressures acting on rigid walls were estimated with the combination of circular and planar failure mechanism, where the backfill followed the nonlinear failure criterion. The solutions of passive earth pressures using the combination of circular and planar failure mechanism were compared with numerical solutions using multi-triangular blocks, which aimed to prove the validity of the present method. The results show that the combination of circular and planar failure mechanism is effective to calculate the passive earth pressure, and that the seismic coefficient and nonlinear parameters have significant influences on the pressure. The nonlinear parameters of backfills have influence on the failure shape of rigid walls.

Key words: nonlinear failure criterion; arc-sandwich failure mechanism; seismic loads; limit analysis; passive earth pressure

研究挡土墙压力问题的主要方法有平衡法、现场实测法、极限分析法等。在线性破坏准则下，Collins等^[1-2]对被动土压力进行了极限分析；Chen^[3]分别采用平动和对数螺旋转动破坏机制计算土压力；Soubra  等^[4-5]将墙后土体划分为单刚块或多刚块体系，应用规划理论及极限分析理论求解被动土压力。然而，大量的实测结果都表明：土体服从非线性破坏准则，线性关系只是其中的一个特例。Lade等^[6-9]在进行三轴试验时发现：土体破坏时的主应力关系是非线性的；因此，如何解决非线性破坏准则下的土压力问题是岩土工程界面临的一项课题。在单个三角形刚块平动破坏机制下，杨小礼等^[10]讨论了非线性破坏准则对被动土压力的影响；在15个三角形刚块平动破坏机制下，Yang等^[11-12]计算出非线性破坏准则及地震作用下被动土压力，并根据上限定理，在非线性破坏准则下分析了不同破坏机制下的主动土压力。以上研究均考虑了非线性破坏准则。在线性破坏准则下，Chen^[3]根据圆弧夹层转动破坏机制计算出被动土压力。挡土墙的被动土压力计算是岩土工程界的一项重要课题，正确地对其进行计算对于确保工程安全至关重要。在此，本文作者引入非线性破坏准则，在Chen^[3]的圆弧夹层转动破坏机制基础上，考虑水平地震作用，计算出圆弧夹层转动破坏机制的非线性能量耗散，求得水平地震作用下的被动土压力的上限解。并与Yang等^[11]三角形刚块平动破坏机制下的结果进行比较，以证明本文结论的正确性。

1  基本原理

土体非线性破坏准则的一般表达式为^[13]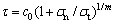：(其中，σ_n和τ分别为破坏面上的正应力和剪应力；c₀为初始黏聚力；σ_t为轴向拉应力；m为非线性系数)。非线性破坏准则的切线方程为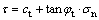：(其中，c_t和tanφ_t分别为切线的斜率和截距)。根据虚功率原理，在所有的机动容许的塑性变形速度场相对应的荷载中，切线方程对应的荷载为真实极限荷载的上限^[14-18]。

2  圆弧夹层破坏机制

2.1  破坏机制的构成

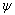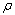如图1所示，土体被划分为3部分，其中：OAB和OCD为直角三角形块；OBC为圆弧辐射受剪区。图1中各参数意义如下：k_h为水平地震系数；v₀为墙体初始运动速度；δ为墙体与填土之间的摩擦角；α为墙体的相对于地面的倾角；β为土体顶面与水平面的夹角；q为地面超载；H为墙体高度；r₀为圆弧半径；为圆弧角；为线OA与OB的夹角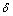；为被动土压力与墙面法线的夹角。

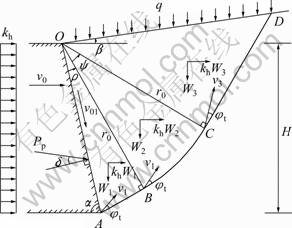
图1  圆弧夹层平动破坏机制图

Fig.1  Translational failure mechanism combination of circular and planar

2.2  外力做功

根据几何关系，由图1可以分别计算出各刚性块边长OA，OB，OC，OD，AB，BC，CD和面积S_OAB，S_OBC，S_OCD以及对应的土体重力W₁，W₂和W₃。根据文献[3]可知v₀, v₁和v₀₁之间的关系式：

             (1)

              (2)

在假定破坏模式下，外力做功功率包括：土体重力功率W_soil，地面超载q的功率W_q，被动土压力的功率W_P，分别计算如下。

(1) 土体重力功率。土体重力功率可以分为OAB，OCD和OBC 3部分进行计算，最后将其叠加即可。基本原理可见文献[3]。

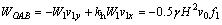      (3)

   (4)

     (5)

土体重力总功率为：

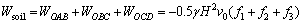   (6)

(2) 地面超载的功率为：

     (7)

(3) 被动土压力的P_P的功率为：

        (8)

所以，外力所作总功率为：

           (9)

2.3  内部能量耗散

内能耗散包括：速度间断线上的能量消耗、墙背填土滑动产生的能量消耗以及圆弧受剪区的能量消耗。基本原理可见文献[3]。

(1) 速度间断线AB和CD的能耗分别为：

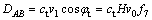         (10)

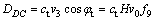         (11)

(2) 墙背填土滑动产生的能耗为：

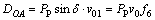        (12)

(3) 圆弧受剪区OBC的能耗为：

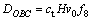             (13)

(4) 圆弧速度间断线BC的能耗。根据文献[3]可知：速度间断线BC上的能耗与圆弧受剪区OBC的能耗几乎相同，所以，总内能耗为：

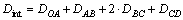      (14)

2.4  被动土压力计算

利用虚功率原理，破坏机制中外力做功与内部耗能的能量相等，

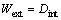              (15)

被动土压力P_p的关系表达式为：

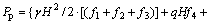
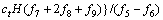         (16)

其中：f₁~f₉是关于ρ，ψ和φ_t的无量纲函数；

；

；

；

；

；

；

；

。

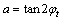
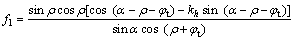
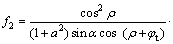
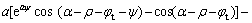
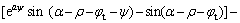
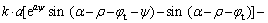
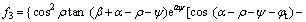
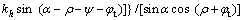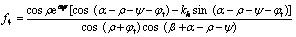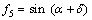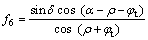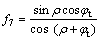3  数值计算与分析

3.1  对比分析

为了验证本文方法的有效性，本文在满足α=90°，β=0°，δ=0°，k_h=0.05，q=0，γ=18 kN/m³，H=4.0 m，c₀=4.0 kPa，σ_t=15.0 kPa的条件下，与Yang等^[11]的多个三角形刚块破坏机制下的被动土压力上限解进行了比较，如表1所示。由表1可以看出：圆弧夹层破坏机制下的被动土压力上限解与文献[11]给出的多三角形刚块破坏机制下的被动土压力很接近，这说明在非线性破坏准则下，采用圆弧破坏机制计算地震荷载作用下的被动土压力是有效的。

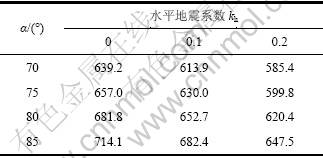
然而，表1只考虑了墙面竖直且填土水平的情况。在实际工程中，墙体大多与地面存在一定倾角α，且β一般大于0°，因此，表2列出了当β=5°，δ=0°，m=1.2，q=0，γ=18 kN/m³，H=4.0 m，c₀=10 kPa，σ_t=30 kPa，且α取70°~85°时的被动土压力。由表2可以看出：当其他参数一定时，被动土压力随着α的增大而增大。

表1  圆弧夹层机制与多刚块机制的被动土压力比较

Table 1  Comparisons of passive earth pressure between composite mechanism and multi-wedge mechanism    kN/m

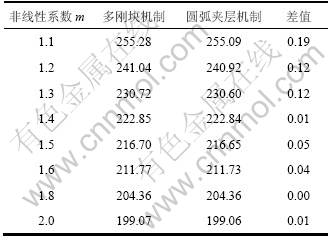
表2  墙体倾斜时的被动土压力

Table 2  Passive earth pressure of inclined walls  kN/m

3.2  地震系数k_h影响

当墙高H=5.0 m时，令α=110°，β=0°，δ=10°，q=0，γ=18 kN/m³，c₀=10 kPa，σ_t=30 kPa，m=1.2~1.8，k_h取0.05~0.30，被动土压力计算结果如图2所示，同时给出m取1.2和1.5时的被动土压力破坏面位置图，见图3~4。由图2可以看出：在其他条件一定的情况下，随着地震系数m的增大，被动土压力P_P有减小的趋势。图3~4则表明：当m及其他参数一定时，水平地震系数越大，破坏面越向外突出。

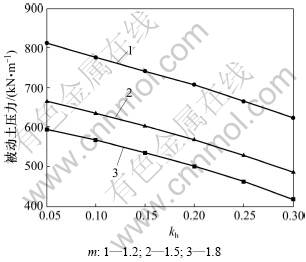
图2  地震系数k_h对被动土压力的影响

Fig.2  Influence of seismic coefficient k_h on passive earth pressure

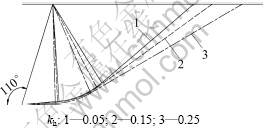
图3  m=1.2时水平地震系数对破坏面位置的影响

Fig.3  Influence of horizontal seismic coefficient on failure surface when m=1.2

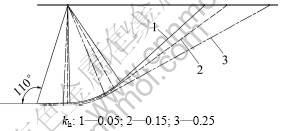
图4  m=1.5时水平地震系数对破坏面位置的影响

Fig.4  Influence of horizontal seismic coefficient on failure surface when m=1.5

3.3  非线性系数m影响

当墙高H=5.0 m时，令α=110°，β=0°，θ=0°，δ=10°，q=0，γ=18 kN/m³，c₀=10 kPa，σ_t=30 kPa，k_h=0.0~0.2，m取1.1~1.6，被动土压力计算结果如图5所示。从图5可以看出：在其他条件一定的情况下，随着m的增大，P_P呈非线性减小趋势。

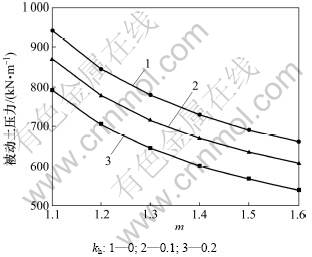
图5  非线性系数m对被动土压力的影响

Fig.5  Influence of nonlinear coefficient m on passive earth pressure

3.4  地面荷载q对破坏面位置的影响

当墙高H=5.0 m时，令α=110°，β=0°，δ=10°，γ=18 kN/m³，c₀=10 kPa，k_h=0.1，σ_t=30 kPa，q=0~40 kPa，m取1.2和1.4，不同超载情况下的被动土压力破坏面位置分别见图6~7。从图6和图7可以看出：当m及其他参数一定时，超载q越大，辐射受剪区域越大，破坏面越向外突出。

3.5  初始黏聚力c₀对破坏面位置的影响

当墙高H=5.0 m时，令α=110°，β=0°，δ=10°，γ=18 kN/m³，q=0，k_h=0.1，σ_t=50 kPa，c₀=20~40 kPa，m取1.2和1.4，不同黏聚力下的被动土压力破坏面位置见图8~9。从图8和图9可以看出：当m及其他参数一定时，随着初始黏聚力c₀的增加，辐射受剪区域有减小的趋势。

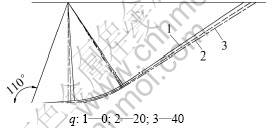
图6  m=1.2时超载对破坏面位置的影响

Fig.6  Influence of surcharge on failure surface when m=1.2

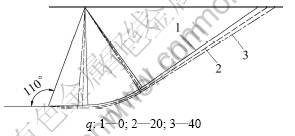
图7  m=1.4时超载对破坏面位置的影响

Fig.7  Influence of surcharge on failure surface when m=1.4

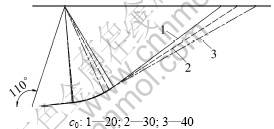
图8  m=1.2时黏聚力对破坏面位置的影响

Fig.8  Influence of initial cohesion on failure surface when m=1.2

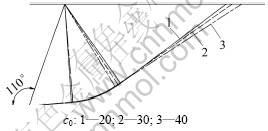
图9  m=1.4时黏聚力对破坏面位置的影响

Fig.9  Influence of initial cohesion on failure surface when m=1.4

3.6  拉应力σ_t对破坏面位置的影响

当墙高H=5.0 m时，令α=110°，β=0°，δ=10°，γ=18 kN/m³，q=0，k_h=0.1，c₀=15kPa，σ_t=30~50 kPa，m取1.2和1.4，不同拉应力情况下的被动土压力破坏面位置见图10~11。从图10和图11可以看出：当m及其他参数一定时，随着拉应力σ_t的增加，辐射受剪区域有增大的趋势。

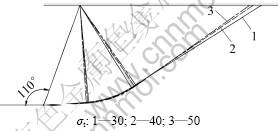
图10  m=1.2时拉应力对破坏面位置的影响

Fig.10  Influence of tensile stress on failure surface when m=1.2

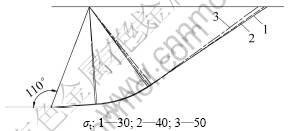
图11  m=1.4时拉应力对破坏面位置的影响

Fig.11  Influence of tensile stress on failure surface when m=1.4

4  结论

(1) 在非线性破坏准则下，圆弧夹层转动破坏机制得出的优化上限解与多个三角形刚块平动破坏机制结果非常接近，这证明了本文结果的正确性。

(2) 水平地震系数与非线性参数对被动土压力均有较为明显的影响。水平地震作用对挡土墙破坏面位置有较明显影响，地震系数越大，圆弧受剪区域面积越小，且破坏面位置越向外突出。

参考文献：

[1] Collins I F. The upper bound theorem for rigid/plastic solids to include Coulomb friction[J]. Journal of the Mechanics and Physics of Solids, 1969, 17(2): 323-328.

[2] Mroz Z, Drescher A. Limit plasticity approach to some cases of flow of bulk solids[J]. Journal of Engineering for Industry, 1969, 91(2): 357-364.

[3] Chen W F. Limit analysis and soil plasticity[M]. Amsterdam: Elsevier, 1975: 10-40.

[4] Soubra A H, Regenass P. Three-dimensional passive earth pressure by kinematical approach[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 26(11): 969-978.

[5] Soubra A H. Static and seismic passive earth pressure coefficients on rigid retaining structure[J]. Canadian Geotechnical Journal, 2000, 37(2): 463-478.

[6] Lade P V. Elasto-plastic stress-strain theory for cohesionless soil with curved yield surface[J]. Int J Solids Structure, 1977, 13(5): 1019-1035.

[7] Hoek E, Brown E. Empirical strength criterion for rock masses[J]. Journal of Geotechnical Engineering Division, ASCE, 1980, 106(9): 1013-1035.

[8] Agar J G, Morgenstern N R, Scott J. Shear strength and stress-strain behavior of Athabasca oil sand at elevated temperatures and pressure[J]. Canadian Geotechnical Journal, 1985, 24(1): 1-10.

[9] YANG Xiao-li, YIN Jian-hua. Slope equivalent Mohr-Coulomb strength parameters for rock masses satisfying the Hoek-Brown criterion[J]. Rock Mechanics and Rock Engineering, 2010, 43(4): 505-511.

[10] 杨小礼, 李亮, 刘宝琛. 非线性破坏准则对被动土压力的影响[J]. 工程力学, 2004, 21(1): 31-36.
YANG Xiao-li, LI-liang, LIU Bao-chen. Influences of a nonlinear failure criterion on passive earth pressure[J]. Engineering Mechanics, 2004, 21(1): 31-36.

[11] YANG Xiao-li, YIN Jian-hua. Estimation of seismic passive earth pressures with nonlinear failure criterion[J]. Engineering Structures, 2006, 28(3): 342-348.

[12] YANG Xiao-li. Upper bound limit analysis of active earth pressure with different fracture surface and nonlinear yield criterion[J]. Theoretical and Applied Fracture Mechanics, 2007, 47(1): 46-56.

[13] Zhang X J, Chen W F. Stability analysis of slopes with general nonlinear failure criterion[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1987, 11(1): 33-50.

[14] Soubra A H. Upper-bound solution for bearing capacity of foundations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(1): 59-68.

[15] Soubra A H, Macuh B. Active and passive earth pressure coefficients by a kinematical approach[J]. Proceeding of the Institution of Civil Engineers, Geotechnical Engineering, 2002, 55(2): 119-131.

[16] Hanna A, Khoury I. Passive earth pressure of over consolidated cohesionless backfill[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(8): 978-986.

[17] YANG Xiao-li. Seismic bearing capacity of a strip footing on rock slopes[J]. Canadian Geotechnical Journal, 2009, 46(8): 943-954.

[18] YANG Xiao-li. Seismic displacement of rock slopes with nonlinear Hoek-Brown failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 948-953.

(编辑 陈灿华)

收稿日期：2010-08-20；修回日期：2010-10-25

基金项目：湖南省自然科学杰出青年基金资助项目(09JJ1008)

通信作者：罗卫华(1970-)，男，湖南邵东人，高级工程师，从事道路工程工作；电话：0730-86299226；E-mail: luoweihua90@vip.sina.com