Transient thermal behavior of radial fins of rectangular, triangular and hyperbolic profiles with temperature-dependent properties using DTM-FDM
来源期刊:中南大学学报(英文版)2017年第3期
论文作者:Sobhan Mosayebidorcheh Mohammad Rahimi-Gorji D. D Ganji Taha Moayebidorcheh O Pourmehran M. Biglarian
文章页码:675 - 682
Key words:transient thermal behavior; radial fin; thermal conductivity; temperature-dependent property; hybrid differential transfor mation-finite difference (DTM-FDM)
Abstract: This work focuses on transient thermal behavior of radial fins of rectangular, triangular and hyperbolic profiles with temperature-dependent properties. A hybrid numerical algorithm which combines differential transformation (DTM) and finite difference (FDM) methods is utilized to theoretically study the present problem. DTM and FDM are applied to the time and space domains of the problem, respectively. The accuracy of this method solution is checked against the numerical solution. Then, the effects of some applicable parameters were studied comparatively. Since a broad range of governing parameters are investigated, the results could be useful in a number of industrial and engineering applications.
Cite this article as: Sobhan Mosayebidorcheh, Mohammad Rahimi-Gorji, D. D Ganji, Taha Moayebidorcheh, O Pourmehran, M. Biglarian. Transient thermal behavior of radial fins of rectangular, triangular and hyperbolic profiles with temperature-dependent properties using DTM-FDM [J]. Journal of Central South University, 2017, 24(3): 675-682. DOI: 10.1007/s11771-017-3468-y.
J. Cent. South Univ. (2017) 24: 675-682
DOI: 10.1007/s11771-017-3468-y
Sobhan Mosayebidorcheh1, Mohammad Rahimi-Gorji2, D. D Ganji3,
Taha Moayebidorcheh1, O Pourmehran2, M. Biglarian4
1. Young Researchers and Elite Club, Najafabad Branch, Islamic Azad University, Najafabad, Iran;
2. Young Researchers and Elite Club, Gorgan Branch, Islamic Azad University, Gorgan, Iran;
3. Mechanical Engineering Department, Babol University of Technology, Babol, Mazandaran, Iran;
4. Department of Mechanical Engineering, Sharif University of Technology, Tehran, Iran
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: This work focuses on transient thermal behavior of radial fins of rectangular, triangular and hyperbolic profiles with temperature-dependent properties. A hybrid numerical algorithm which combines differential transformation (DTM) and finite difference (FDM) methods is utilized to theoretically study the present problem. DTM and FDM are applied to the time and space domains of the problem, respectively. The accuracy of this method solution is checked against the numerical solution. Then, the effects of some applicable parameters were studied comparatively. Since a broad range of governing parameters are investigated, the results could be useful in a number of industrial and engineering applications.
Key words: transient thermal behavior; radial fin; thermal conductivity; temperature-dependent property; hybrid differential transfor mation-finite difference (DTM-FDM)
1 Introduction
Heat transfer is an important phenomenon that occurs in many processes. The most effective instrument for increasing the rate of heat transfer is a fin which can cause an increase in the transferred heat amount by increasing the area of heat transfer. Extended surfaces are extensively used in various applications such as refrigeration, air conditioning, automobile, heat exchanger, electrical chips and chemical processing equipment. There exist various types of the fins, such as rectangular, triangle, hyperbolic profile and most often constant thermophysical properties are often assumed in modeling. However, in reality most of properties and natural phenomena are inherently variable, i.e. non-constant, and therefore nonlinear. For ordinary fin problems, the thermal conductivity is assumed to be constant, but when a large temperature difference exists within a fin, the thermal conductivity varies from the base to the tip of fin; the variation is dependent on the material of the fin. Furthermore, in real operating conditions, the local convective heat transfer is a nonlinear function of the local temperature difference driving the convection process.
There exists little literature on the performance of radial and longitudinal fins attached to a stationary base surface. KRAUS et al [1] provided a detailed discussion of the mathematical models and their solutions for radial fins of rectangular, triangular and hyperbolic profile shapes operating under a variety of thermal boundary conditions. KUNDU [2] analytically studied the performance and optimization of longitudinal and pin fins of step reduction in local cross-section (SRC) profile subject to combined heat and mass transfer.
There are some simple and accurate approximation techniques for solving differential equations of fins. The thermal analysis of the radial and straight fins considering temperature-dependent thermal conductivity is investigated by the variational iteration method (VIM) [3]. DOMAIRRY and FAZELI [4] solved the nonlinear straight fin differential equations by homotopy analysis method (HAM) to evaluate the temperature distribution within the fin. ARSLANTURK [5] obtained correlation equations for optimum design of annular fins with temperature-dependent thermal conductivity. KHANI et al [6] used HAM to evaluate the analytical approximate solutions and efficiency of the nonlinear fin problem with temperature-dependent thermal conductivity and heat transfer coefficient. KUNDU [2] described an analytical method for temperature and heat transfer characteristics of an annular step fin (ASF) with the simultaneous heat and mass transfer mechanisms. BOUAZIZ and AZIZ [7] introduced a new concept F called the double optimal linearization method (DOLM) to derive simple and accurate expressions for predicting the thermal performance of a convective-radiative fin with temperature-dependent thermal conductivity. KHANI and AZIZ [8] used HAM to develop analytical solutions for the thermal performance of a straight fin of trapezoidal profile when both thermal conductivity and heat transfer coefficient are temperature-dependent.
The differential transformation method (DTM) is utilized to solve the non-linear governing equation. DTM is a semi-numerical-analytical method which is based on the Taylor series expansion first introduced by ZHOU [9] in 1986 for the solution of linear and nonlinear initial value problems. This method can be applied directly to linear and nonlinear differential equations without requiring linearization, discretization or perturbation and this is the main benefit of this method. The method was subsequently used to obtain analytical solutions of higher-order ordinary differential equations, partial differential equations, difference equations, and integro- differential equations. RAHIMI-GORJI et al [10] carried out an analytical investigation on the heat transfer for the microchannel heat sink (MCHS) cooled by different nanofluids and optimized its geometry using RSM analysis. POURMEHRAN et al [11] investigated a thermal and flow analysis of a fin shaped microchannel heat sink (MCHS) cooled by different nano-fluids based on saturated porous medium and least square method and then results were compared with numerical procedure. RAHIMI-GORJI et al [12] demonstrated unsteady motion of a rigid spherical particle in a quiescent shear- thinning power-law fluid using collocation method (CM) and the established numerical method (fourth-order Runge–Kutta) scheme. Several studies have been performed on heat transfer and nonlinear equations [13-19]. Today numerical and analytical methods are applied for computer simulation to many phenomena [20-23]. MOSAYEBIDORCHEH et al [24] evaluated the analytical solution of the nonlinear fin problem with temperature-dependent thermal conductivity by using DTM. Furthermore, in general, the heat transfer coefficient may vary along a fin.FOULADI et al [25] utilized the VIM as an approximate analytical technique to analyze straight fins with variable heat transfer coefficient. A numerical study of thermal performance of a convective-radiative fin with simultaneous variation of thermal conductivity, heat transfer coefficient, and surface emissivity with temperature was conducted by AZIZ and TORABI [26]. Also they evaluated the thermal performance and efficiency of T-shaped fins considering temperature-dependent properties for both stem and flange parts [27]. TORABI et al [28] investigated the thermal performance of the longitudinal fins of rectangular, trapezoidal and concave parabolic profiles. AZIZ et al [29] studied the convective-radiative radial fins for homogeneous and functionally graded materials (FGM). The boundary conditions of their analysis are considered the convective base heating and convective-radiative tip cooling. HATAMI et al [30, 31] presented the thermal analysis of circular convective- radiative porous fins with different section shapes and materials. Also, heat transfer study through porous fins (Si3N4 and Al) considering temperature- dependent heat generation has been investigated in Ref. [32]. Recently, transient response of the longitudinal rectangular fins has been investigated using the symmetry analysis [33, 34].
MOSAYEBIDORCHEH et al [34] studied the transient thermal analysis of longitudinal fins with variable cross section considering internal heat generation. They considered the profile shapes of the fins rectangular, convex, triangular and concave. Also they assumed that both thermal conductivity and internal heat generation are as linear functions of temperature. In their work, the power-law temperature-dependent model is used to simulate different types of heat transfer such as laminar film boiling, natural convection, nucleate boiling and radiation.
This investigation considers transient thermal behavior of radial fins of rectangular, triangular and hyperbolic profiles with temperature-dependent properties. Thermal conductivity and internal heat generation are regarded as linear functions of temperature, while convection heat transfer coefficient is considered a power-law function of temperature. A hybrid numerical algorithm which combines DTM and finite difference method (FDM) is utilized to study the present problem. DTM and FDM are applied to the time and space domains of the problem, respectively.
2 Differential transform method
The differential transform is defined as
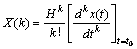 (1)
(1)
where x(t) is an analytical function in the time domain; H is the time interval; X(k) is the transformed function. The inverse transformation is
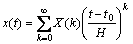 (2)
(2)
Substituting Eq. (1) into Eq. (2), we can obtain the Taylor series expansion of x(t) at t0
 (3)
(3)
The function x(t) is usually considered a series with limited terms and Eq. (2) can be rewritten as
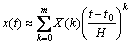 (4)
(4)
where m represents the number of Taylor series’ components. Usually, through elevating this value, the accuracy of the solution can be increased.
Some of the properties of DTM have been shown in Table 1 [35]. These properties are extracted from Eqs. (1) and (3). Some engineering problems have been solved using this technique [24, 34, 35].
Table 1 Properties of DTM [35]

3 Problem description
The problem to be studied is the one-dimensional heat transfer in radial fins of rectangular, triangular and hyperbolic profiles with variable cross section Ac and arbitrary profile F(R) as shown in Fig. 1. Suppose that the temperature of the ambient air is Ta and fin isattached to a fixed prime surface with the temperature Tb. The thickness of base fin is denoted by δb. The fin is initially at temperature Tb. The temperature of the base fin is kept at Tb. Ignoring the change of cross section, the energy balance equation of the fin, based on the one- dimensional heat conduction, is given by
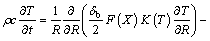
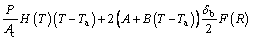 (5)
(5)
where ρ is density; c is specific heat capacity; R is space variable; t is time; T is temperature.
The fin’s thermal conductivity K, the convective heat transfer coefficient H and the internal heat generation are assumed to be functions of temperature. A and B are the constant and temperature-dependent terms of the internal heat generation, respectively. The fin tip is assumed to be adiabatic.
The internal heat generation is per unit volume, so it has a direct relation with the fin profile.
The boundary conditions of constant base temperature and adiabatic tip are:
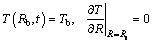 (6)
(6)
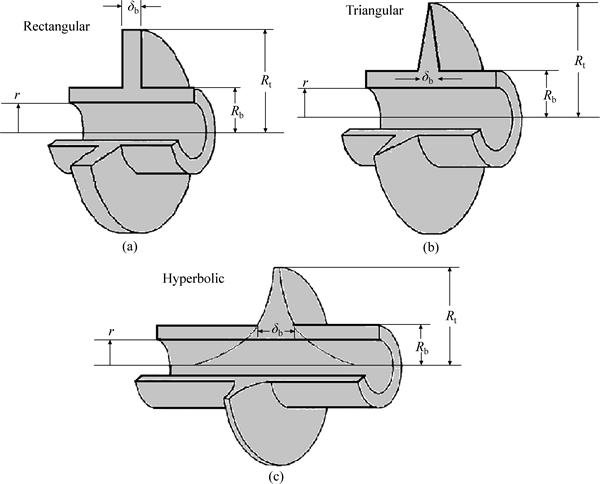
Fig. 1 Configuration of different radial fin profiles
where Rb and Rt are the radii of the fin base and fin tip, respectively. The initial temperature of the fin is equal to the temperature T0:
 (7)
(7)
By introducing the following dimensionless parameters,
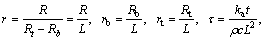
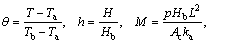
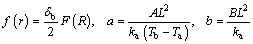 (8)
(8)
Eq. (5) reduces to
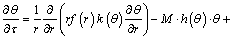
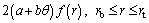 (9)
(9)
where M is the thermo-geometric fin factor; r is the dimensionless space variable; ka is the thermal conductivity of the fin at ambient temperature; k is the dimensionless thermal conductivity; hb is the heat transfer coefficient at the fin base; θ is the dimensionless temperature.
The boundary conditions in the dimensionless form are:
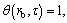
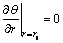 (10)
(10)
And the dimensionless initial condition is
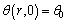 (11)
(11)
The heat transfer coefficient is given by the power law model [36, 37]:
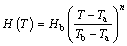 (12)
(12)
where n and hb are the constants of the model. The parameter n can be varied between -6.6 and 5 [36]. Also, the thermal conductivity may be given as a linear temperature-dependent function [30]:
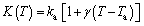 (13)
(13)
The dimensionless forms of the heat transfer coefficient and thermal conductivity are  and k(θ)=1+βθ, respectively; and so the thermal conductivity gradient is
and k(θ)=1+βθ, respectively; and so the thermal conductivity gradient is 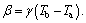 The dimensionless heat transfer equation of problem is given by
The dimensionless heat transfer equation of problem is given by
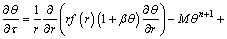
 (14)
(14)
where f(r) is the dimensionless profile of the fin.
4 Application of hybrid DTM-FDM
Equation (14) has been solved using the hybrid DTM-FDM. Details of this method’s solution procedure have been provided in Ref. [9]. This method is applied in some engineering problems, such as transient thermal analysis of longitudinal fins with internal heat generation [34], transient advective–dispersive transport Eq. [38], free vibration of a plate [39], thermal analysis of annular fin with temperature-dependent thermal conductivity [40], large deflections of orthotropic rectangular plate [41] and nonlinear transient heat conduction problems [42, 43].
To solve the nonlinear partial equations (Eq. (14)) in the domain and
and 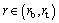 using hybrid DTM and FDM, we apply the finite difference approximation to r direction and take DTM to t. The following finite difference scheme is used based on a uniform mesh. The length of the direction of r is divided into Nr equal intervals. The r coordinates of the grid points can be obtained by
using hybrid DTM and FDM, we apply the finite difference approximation to r direction and take DTM to t. The following finite difference scheme is used based on a uniform mesh. The length of the direction of r is divided into Nr equal intervals. The r coordinates of the grid points can be obtained by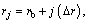 j=0:Nr , where Δr is the mesh size.
j=0:Nr , where Δr is the mesh size.
After taking second-order accurate central finite difference approximation with respect to r and applying DTM on Eq. (14) for the time domain, the following recurrence relations can be obtained:
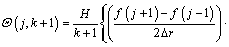
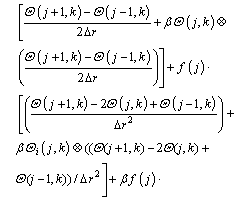
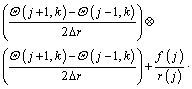
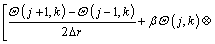
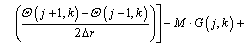
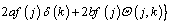 (15)
(15)
where the symbol ‘‘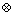 ’’ denotes the convolution operation and G(j, k) is the differential transform of the function g(θ)=θ n+1.
’’ denotes the convolution operation and G(j, k) is the differential transform of the function g(θ)=θ n+1.
Applying DTM to the initial condition in Eq. (11), we have:
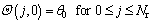 (16)
(16)
The boundary conditions in Eq. (10) can be transformed as
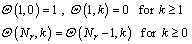 (17)
(17)
5 Results and discussions
In this study, hybrid DTM-FDM is used to solve the problem of transient thermal behavior of radial fins of rectangular, triangular and hyperbolic profiles with temperature-dependent properties (Fig. 1). These active parameters, such as fin profiles, heat transfer coefficient and internal heat generation have effects on the temperature distribution. In this research, the shape of the fin is assumed as a rectangular profile (f(r)=1), hyperbolic profile (f(r)=rb/r) and triangular profile (f(r)=rt-r).
The code is validated by comparing the obtained results of numerical solutions. The comparison shows a good agreement (Fig. 2) which proves the validity of this method to be applied to engineering problems. Figure 2 shows the temperature distribution within fins for constant (rectangular) and variable (triangular and hyperbolic) cross sections at τ=0.3. The Maple package uses FDM to discretize the differential equation. This technique is a centered implicit scheme and is capable of finding solutions to higher-order PDE and PDE systems. It is considered that β is less than zero in Fig. 2. It is important to note that β depicts the change in the thermal conductivity as a function of temperature. The positive and negative β numbers have different effects on the thermal conductivity, depending on the material of fins and the thermal conductivity might decrease (β<0) or increase (β>0) with temperature. As seen in Fig. 2, the profile shape of fins has an important role in temperature distribution especially near the fin tip (0.5≤r-rb≤1). The fin surface temperature decreases from the rectangular profile to triangular profile, then to hyperbolic profile. In other words, the best profile in this category is the hyperbolic shape because it has the maximum heat transfer and the minimum fin temperature. It can be said that decreasing area of the fin in radial direction causes to decrease the fin temperature (or increase the heat transfer from the fin surface).
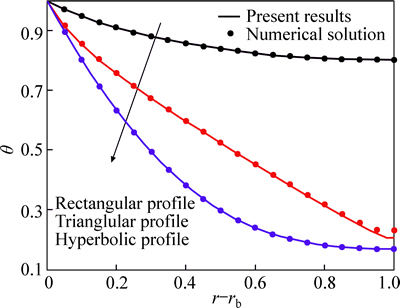
Fig. 2 Comparison of results of hybrid DTM-FDM and numerical solutions at τ=0.3 when β=-0.6, M=2, a=1, b=0.5, rb=0.1, θ0=0.1 and n=2
Figure 3 depicts the effect of the nature of heat transfer on transient temperature distribution for five different regimes of fluid flow on the fins. For showing different regimes, the exponent n (associated with the convective heat transfer coefficient) should be changed. The exponent n characterizes condensation or laminar film boiling (n=-1/4), laminar natural convection (n=1/4), turbulent natural convection (n=1/3), nucleate boiling (n=2) and radiation heat transfer (n=3). As seen in Figs. 3(a) to (c), the effects of the nature of heat transfer on transient temperature distribution for different regimes of fluid flow on different shapes of fins (rectangular, triangular and hyperbolic profile) are shown. Fin surface temperature associated with the nature of the heat transfer is shown in Fig. 3. The temperature distribution of the fin is an increasing function of exponent n for all profiles. The minimum and maximum fin surface temperatures are the laminar film boiling and radiation heat transfer, respectively. These results have similar trend for all three profiles. The stability or instability can be influenced by physical parameters of heat transfer such as thermal conductivity and heat transfer coefficient. The thermal instability can be observed in the temperature distribution of triangular profile (see Fig. 3(b)).
In Fig. 4, the effect of internal heat generation on the temperature distribution in fin with thermal conductivity increasing with temperature at τ=0.4 is indicated for six cases.
In this figure, the nucleate film boiling (n=2) is considered for the hyperbolic fin profile. The parameter a is the constant term of internal heat generation, while the parameter b is the linear temperature-dependent term of internal heat generation. The value of heat generation Figure 4 confirms that increasing the internal heat generation (a) leads to an increase in fin surface temperature to base temperature or more. In fact, themight decrease (b<0) or increase (b>0) with temperature. gradient temperature in the base of the fins is always negative except for the existing high heat generation (see Fig. 4 for a≥2).
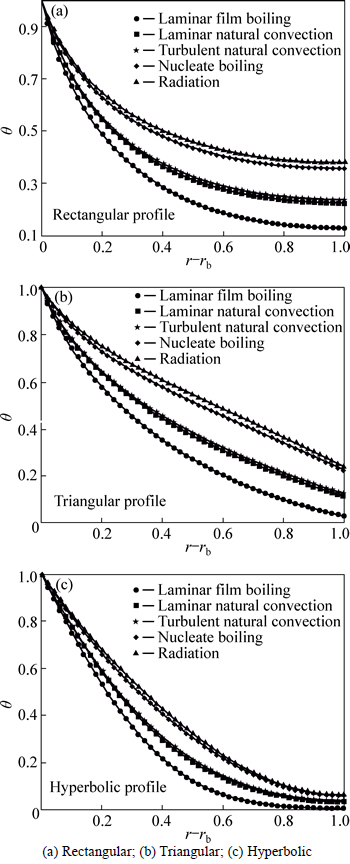
Fig. 3 Effect of nature of heat transfer on transient temperature distribution at τ=0.6 when β=0.3, M=3, a=0.1, b=-0.5, rb=0.1 and θ0=0:
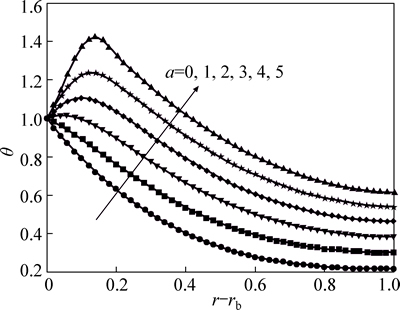
Fig. 4 Transient temperature distribution at τ=0.4 when β=0.7, M=1, b=1, rb=0.1, θ0=0.2 and n=2 for hyperbolic profile
The figure of the fin temperature in different time for rectangular profile to analyze the transient behavior of the fin temperature is shown in Fig. 5. This figure depicts the time dependency of fin temperature. As seen in this figure, the fin temperature increases with time passing. This occurs because of the internal heat generation and the fin temperature may be reached to base temperature or more.
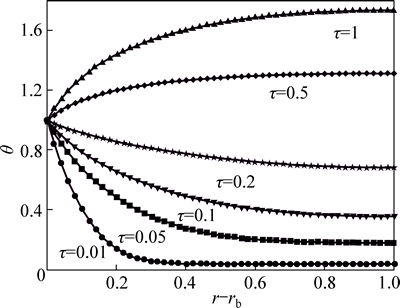
Fig. 5 Transient temperature distribution at different times when β=0.2, M=3, a=2, b=0.5, rb=0.1, θ0=0 and n=-1/4 for rectangular profile
One of the important parameters influencing temperature distribution is convection heat transfer coefficient at base temperature (M). Figure 7 demonstrates the effect of this parameter on temperature distribution. This figure confirms that for fin with low M at first by increase in M, the temperature distribution has increased and then with increase in M, the temperature distribution has decreased. This means that for fin with low M, the temperature near the base fin reaches to its maximum. For fin with high M, in whole region of fin by increase in M, the temperature distribution increases.

Fig. 6 Transient temperature distribution at τ=1.8 when β=0.5, a=2, b=0.1, rb=0.1, θ0=0 and n=1/4 for hyperbolic profile
Figure 7 depicts the gradient temperature at the fin base for different profiles. As seen, the maximum gradient temperature is for rectangular profile. The temperature near the base fin reaches to steady state at τ=0.5, but then the temperature in the fin tip reaches to steady state.This applies to all three profiles.
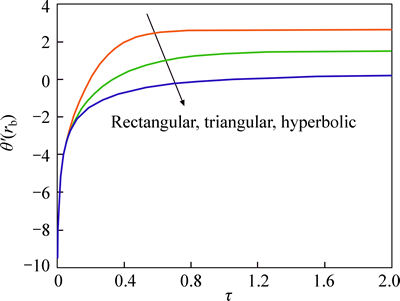
Fig. 7 Gradient temperature at fin base when β=-0.4, M=1, a=2, b=0.1, rb=0.1, θ0=0.05 and n=2 for different profiles
6 Conclusion
Transient thermal behavior of radial fins of rectangular, triangular and hyperbolic profiles with temperature-dependent properties is investigated. Thermal conductivity and internal heat generation are assumed temperature-dependent. Hybrid DTM-FDM is utilized to study the present problem. The results show that this method provides good agreement with previous numerical solutions of this nonlinear equation. The profile shape of fins has an important role in temperature distribution especially near the fin tip. The best profile in this category is the hyperbolic shape because it has the maximum heat transfer and the minimum fin temperature. Also, results show that the fin surface temperature is greatly dependent on the nature of the heat transfer. The laminar film boiling and radiation heat transfer have the minimum and maximum fin surface temperatures, respectively.
References
[1] KRAUS A D, AZIZ A, WELTY J. Extended surface heat transfer [M]. Canada: John Wiley & Sons, 2002.
[2] KUNDU B. Analysis of thermal performance and optimization of concentric circular fins under dehumidifying conditions [J]. International Journal of Heat and Mass Transfer, 2009, 52: 2646-2659.
[3]  S B, ATAY M T. Analysis of convective straight and radial fins with temperature-dependent thermal conductivity using variational iteration method with comparison with respect to finite element analysis [J]. Mathematical Problems in Engineering, 2007, Article ID 42072: 15 pages.
S B, ATAY M T. Analysis of convective straight and radial fins with temperature-dependent thermal conductivity using variational iteration method with comparison with respect to finite element analysis [J]. Mathematical Problems in Engineering, 2007, Article ID 42072: 15 pages.
[4] DOMAIRRY G, FAZELI M. Homotopy analysis method to determine the fin efficiency of convective straight fins with temperature-dependent thermal conductivity [J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 14: 489-499.
[5] ARSLANTURK C. Correlation equations for optimum design of annular fins with temperature dependent thermal conductivity [J]. Heat and Mass Transfer, 2009, 45: 519-525.
[6] KHANI F, RAJI M A, NEJAD H H. Analytical solutions and efficiency of the nonlinear fin problem with temperature-dependent thermal conductivity and heat transfer coefficient [J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 14: 3327-3338.
[7] BOUAZIZ M, AZIZ A. Simple and accurate solution for convective–radiative fin with temperature dependent thermal conductivity using double optimal linearization [J]. Energy Conversion and Management, 2010, 51: 2776-2782.
[8] KHANI F, AZIZ A. Thermal analysis of a longitudinal trapezoidal fin with temperature-dependent thermal conductivity and heat transfer coefficient [J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15: 590-601.
[9] ZHOU J. Differential transformation and its applications for electrical circuits [M]. Wuhan: Huazhong University Press, 1986. (in Chinese)
[10] RAHIMI-GORJI M, POURMEHRAN O, HATAMI M, GANJI D. Statistical optimization of microchannel heat sink (MCHS) geometry cooled by different nanofluids using RSM analysis [J]. The European Physical Journal Plus, 2015, 130: 1-21.
[11] POURMEHRAN O, RAHIMI-GORJI M, HATAMI M, SAHEBI S, DOMAIRRY G. Numerical optimization of microchannel heat sink (MCHS) performance cooled by KKL based nanofluids in saturated porous medium [J]. Journal of the Taiwan Institute of Chemical Engineers, 2015, 55: 49-68.
[12] RAHIMI-GORJI M, POURMEHRAN O, GORJI-BANDPY M, GANJI D. An analytical investigation on unsteady motion of vertically falling spherical particles in non-Newtonian fluid by Collocation Method [J]. Ain Shams Engineering Journal, 2014, 6: 531-540.
[13] ABUTEEN E, MOMANI S, ALAWNEH A. Solving the fractional nonlinear Bloch system using the multi-step generalized differential transform method [J]. Computers & Mathematics with Applications, 2014, 68: 2124-2132.
[14] POURMEHRAN O, RAHIMI-GORJI M, GORJI-BANDPY M, GANJI D. Analytical investigation of squeezing unsteady nanofluid flow between parallel plates by LSM and CM [J]. Alexandria Engineering Journal, 2015, 54: 17-26.
[15] JONEIDI A, GANJI D, BABAELAHI M. Differential transformation method to determine fin efficiency of convective straight fins with temperature dependent thermal conductivity [J]. International Communications in Heat and Mass Transfer, 2009, 36: 757-762.
[16] RASHIDI M M, LARAQI N, SADRI S M. A novel analytical solution of mixed convection about an inclined flat plate embedded in a porous medium using the DTM-Padé [J]. International Journal of Thermal Sciences, 2010, 49: 2405-2412.
[17] RASHIDI M M, POUR S M. A novel analytical solution of steady flow over a rotating disk in porous medium with heat transfer by DTM-Padé [J]. African Journal of Mathematics and Computer Science Research, 2010, 3: 93-100.
[18] WANG C C, YAU H T. Application of the differential transformation method to bifurcation and chaotic analysis of an AFM probe tip [J]. Computers & Mathematics with Applications, 2011, 61: 1957-1962.
[19] YAGHOOBI H, TORABI M. The application of differential transformation method to nonlinear equations arising in heat transfer [J]. International Communications in Heat and Mass Transfer, 2011, 38: 815-820.
[20] RAHIMI-GORJI M, POURMEHRAN O, GORJI-BANDPY M, GORJI T B. CFD simulation of airflow behavior and particle transport and deposition in different breathing conditions through the realistic model of human airways [J]. Journal of Molecular Liquids, 2015, 209: 121-133.
[21] POURMHRAN O, RAHIMI-GORJI M, GORJI-BANDPY M, GORJI T B. Simulation of magnetic drug targeting through tracheobronchial airway in presence of an external non-uniform magnetic field using Lagrangian magnetic particle tracking [J]. Journal of Magnetism and Magnetic Materials, 2015, 393: 380-393.
[22] POURMEHRAN O, RAHIMI-GORJI M, GORJI-BANDPY M, BAOU M. Comparison between the volumetric flow rate and pressure distribution for different kinds of sliding thrust bearing [J]. Propulsion and Power Research, 2015, 4: 84-90.
[23] RAHIMI-GORJI M, GHAJAR M, KAKAEE AMIR-HASAN, DAVOOD DOMIRI GANJI. Modeling of the air conditions effects on the power and fuel consumption of the SI engine using neural networks and regression [J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2016, DOI: 10.1007/s40430-016-0539-1.
[24] MOSAYEBIDORCHEH S, MOSAYEBIDORCHEH T. Series solution of convective radiative conduction equation of the nonlinear fin with temperature dependent thermal conductivity [J]. International Journal of Heat and Mass Transfer, 2012, 55: 6589-6594.
[25] FOULADI F, HOSSEINZADEH E, BARARI A, DOMAIRRY G. Highly nonlinear temperature-dependent fin analysis by variational iteration method [J]. Heat Transfer Research, 2010, 41: 155-165.
[26] AZIZ A, TORABI M. Convective-radiative fins with simultaneous variation of thermal conductivity, heat transfer coefficient, and surface emissivity with temperature [J]. Heat Transfer—Asian Research, 2012, 41: 99-113.
[27] TORABI M, AZIZ A. Thermal performance and efficiency of convective–radiative T-shaped fins with temperature dependent thermal conductivity, heat transfer coefficient and surface emissivity [J]. International Communications in Heat and Mass Transfer, 2012, 39: 1018-1029.
[28] TORABI M, AZIZ A, ZHANG K. A comparative study of longitudinal fins of rectangular, trapezoidal and concave parabolic profiles with multiple nonlinearities [J]. Energy, 2013, 51: 243-256.
[29] AZIZ A, TORABI M, ZHANG K. Convective–radiative radial fins with convective base heating and convective–radiative tip cooling: Homogeneous and Functionally graded materials [J]. Energy Conversion and Management, 2013, 74: 366-376.
[30] HATAMI M, GANJI D. Thermal performance of circular convective–radiative porous fins with different section shapes and materials [J]. Energy Conversion and Management, 2013, 76: 185-193.
[31] HATAMI M, HASANPOUR A, GANJI D. Heat transfer study through porous fins (Si3N4 and Al) with temperature-dependent heat generation [J]. Energy Conversion and Management, 2013, 74: 9-16.
[32] MOITSHEKI R J, BRADSHAW-HAJEK B H. Symmetry analysis of a heat conduction model for heat transfer in a longitudinal rectangular fin of a heterogeneous material [J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18: 2374-2387.
[33] MHLONGO M, MOITSHEKI R, MAKINDE O. Transient response of longitudinal rectangular fins to step change in base temperature and in base heat flow conditions [J]. International Journal of Heat and Mass Transfer, 2013, 57: 117-125.
[34] MOSAYEBIDORCHEH S, FARZINPOOR M, GANJI D. Transient thermal analysis of longitudinal fins with internal heat generation considering temperature-dependent properties and different fin profiles [J]. Energy Conversion and Management, 2014, 86: 365-370.
[35] MOSAYEBIDORCHEH S. Solution of the boundary layer equation of the power-law pseudoplastic fluid using differential transform method [J]. Mathematical Problems in Engineering, 2013, Article ID685454: 8 pages.
[36] NDLOVU P L, MOITSHEKI R J. Application of the two-dimensional differential transform method to heat conduction problem for heat transfer in longitudinal rectangular and convex parabolic fins [J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18: 2689-2698.
[37]  NAL H. An analytic study of boiling heat transfer from a fin [J]. International Journal of Heat and Mass transfer, 1987, 30: 341-349.
NAL H. An analytic study of boiling heat transfer from a fin [J]. International Journal of Heat and Mass transfer, 1987, 30: 341-349.
[38] JU S P. Application of differential transformation to transient advective–dispersive transport equation [J]. Applied Mathematics and Computation, 2004, 155: 25-38.
[39] YEH Y L, JANG M J, WANG C C. Analyzing the free vibrations of a plate using finite difference and differential transformation method [J]. Applied Mathematics and Computation, 2006, 178: 493-501.
[40] PENG H S, CHEN C L. Hybrid differential transformation and finite difference method to annular fin with temperature-dependent thermal conductivity [J]. International Journal of Heat and Mass Transfer, 2011, 54: 2427-2433.
[41] YEH Y L, WANG C C, JANG M J. Using finite difference and differential transformation method to analyze of large deflections of orthotropic rectangular plate problem [J]. Applied Mathematics and Computation, 2007, 190: 1146-1156.
[42] CHU H P, LO C Y. Application of the hybrid differential transform-finite difference method to nonlinear transient heat conduction problems [J]. Numerical Heat Transfer, Part A: Applications, 2007, 53: 295-307.
[43] CHU H P, CHEN C L. Hybrid differential transform and finite difference method to solve the nonlinear heat conduction problem [J]. Communications in Nonlinear Science and Numerical Simulation, 2008, 13: 1605-1614.
(Edited by YANG Hua)
Cite this article as: Sobhan Mosayebidorcheh, Mohammad Rahimi-Gorji, D. D Ganji, Taha Moayebidorcheh, O Pourmehran, M. Biglarian. Transient thermal behavior of radial fins of rectangular, triangular and hyperbolic profiles with temperature-dependent properties using DTM-FDM [J]. Journal of Central South University, 2017, 24(3): 675-682. DOI: 10.1007/s11771-017-3468-y.
Received date: 2015-04-11; Accepted date: 2015-12-10
Corresponding author: Mohammad Rahimi-Gorji; Tel: +98-111-3234205; E-mail: m69.rahimi@yahoo.com

