Analytical investigation of temperature of a single micron sized iron particle during combustion
来源期刊:中南大学学报(英文版)2020年第3期
论文作者:Peyman MAGHSOUDI Mehdi BIDABADI Seyed Amir Hossein MADANI Abolfazl AFZALABADI
文章页码:951 - 962
Key words:iron particle combustion; analytical solutions; thermal radiation; convective heat transfer
Abstract: The present study deals with analytical investigation of temperature of a single burning iron particle. Three mathematical methods including AGM (Akbari-Ganji’s method), CM (Collocation method) and GM (Galerkin Method) are applied to solving non-linear differential governing equation and effectiveness of these methods is examined as well. For further investigation, forth order Runge-Kutta approach, a numerical method, is used to validate the obtained analytical results. In the present study, the developed mathematical model takes into account the effects of thermal radiation, convective heat transfer and particle density variations during combustion process. Due to particles’ small size and high thermal conductivity, the system is assumed to be lumped in which the particle temperature does not change within the body and all of its regions are at the same temperature. The temperature distributions obtained by analytical methods have satisfactory agreement with numerical outputs. Finally, the results indicate that AGM is a more appropriate method than GM and CM due to its lower mean relative error and less run time.
Cite this article as: Peyman MAGHSOUDI, Mehdi BIDABADI, Seyed Amir Hossein MADANI, Abolfazl AFZALABADI. Analytical investigation of temperature of a single micron sized iron particle during combustion [J]. Journal of Central South University, 2020, 27(3): 951-962. DOI: https://doi.org/10.1007/s11771-020-4343-9.

J. Cent. South Univ. (2020) 27: 951-962
DOI: https://doi.org/10.1007/s11771-020-4343-9
Peyman MAGHSOUDI, Mehdi BIDABADI, Seyed Amir Hossein MADANI, Abolfazl AFZALABADI
Department of Energy Conversion, School of Mechanical Engineering, Iran University of Science and Technology (IUST), Narmak, 16846-13114, Tehran, Iran
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract: The present study deals with analytical investigation of temperature of a single burning iron particle. Three mathematical methods including AGM (Akbari-Ganji’s method), CM (Collocation method) and GM (Galerkin Method) are applied to solving non-linear differential governing equation and effectiveness of these methods is examined as well. For further investigation, forth order Runge-Kutta approach, a numerical method, is used to validate the obtained analytical results. In the present study, the developed mathematical model takes into account the effects of thermal radiation, convective heat transfer and particle density variations during combustion process. Due to particles’ small size and high thermal conductivity, the system is assumed to be lumped in which the particle temperature does not change within the body and all of its regions are at the same temperature. The temperature distributions obtained by analytical methods have satisfactory agreement with numerical outputs. Finally, the results indicate that AGM is a more appropriate method than GM and CM due to its lower mean relative error and less run time.
Key words: iron particle combustion; analytical solutions; thermal radiation; convective heat transfer
Cite this article as: Peyman MAGHSOUDI, Mehdi BIDABADI, Seyed Amir Hossein MADANI, Abolfazl AFZALABADI. Analytical investigation of temperature of a single micron sized iron particle during combustion [J]. Journal of Central South University, 2020, 27(3): 951-962. DOI: https://doi.org/10.1007/s11771-020-4343-9.
1 Introduction
The possibility of a dust explosion in the exposed industrial sites has made that the scientists recognize this danger and devise precautions in order to prevent this incident. The specific accidents have been continuously reported since 150 years ago which shows not only a historic issue, but also a challenging problem, because it has not been solved yet [1].
A low concentration of solid particles is exposed to the risk of being exploded if the particles are dispersed properly in air and ignited by an unintentional external source. In this condition, the flame rapidly passes through the disposed environment and causes severe human and financial damages. This phenomenon involves a wide variety of sites and factories working with flour, plastics, wood, coal and metals [2-4]. The most iterated explosions are the ones where metal particles are involved, encompassing 24% of all [5].
With the development of industrial processes and progressive usage of powder in technology, it is more important than ever to recognize the threats and establish preventive actions in order to maintain safety. Therefore, better understanding of the details is necessary to decrease the probability of occurrence of dust explosions.
Moreover, the combustion of particles has drawn a great amount of attention from the researchers which is caused by the inevitable shortage of fossil fuels and the increasing urgent need for energy in near future [6]. In spite of the efforts conducted to analyze the combustion characteristics of metal particles, there are still unknown issues to be clarified [7].
Among all materials, iron is widely studied in the context due to its abundancy. Iron is utilized for synthesizing of liquid hydrocarbons as a catalyst [8] and NOx control [9]. The byproduct of iron combustion, iron oxide, can be collected and recycled using existing metal smelters or novel technological processes powered by green power sources [10]. The kinetics of the reaction occurring between iron and air is so challenging due to its complicated reaction chains and the mechanism in which iron burns from the surface. Also, providing proper experimental conditions is another obstacle.
Many researches which have been carried out on iron particles combustion are concerned about flame propagation through a dispersed dust of particles both experimentally and analytically and few specific studies are executed to solely discuss the combustion of a single iron particle. TANG et al [11] performed experiments in a reduced gravity condition during a flight in order to estimate the quenching distance, flame speed and temperature of a rich iron dust suspension in air. TANG et al [12] also conducted the so-called argon/helium experiment to distinguish the combustion modes of iron particles. In a series of studies, SUN et al [13-16] investigated the combustion characteristics of the iron particles such as maximum and flame temperature, flame propagation speed. They examined the effect of particle diameter on the burning time as well as temperature profile and flame speed as a function of dust concentration. BROUMAND et al [17] analytically studied the burning velocities of micro particles of the iron regarding their concentration across a vertical duct. Their results showed that the concentration of particles at the leading edge of combustion zone influences the flammability limits more than the ones which are far from the flame front.
In the mathematical modeling of thermal science problems, the governing equations consist of ordinary and partial differential equations which in some cases are nonlinear and cannot be solved by analytical solutions. To overcome this problem, researchers have proposed different approaches to solve non-linear differential equations [18-22]. Some of the suggested methods are Homotopy Perturbation method [23, 24], differential transformation method [25], homotopy analysis method [26], Adomian’s decomposition method [27], variational iteration method [28], Akbari- Ganji’s method [29, 30], least square method [31], Galerkin method [32] and collocation method [33]. GHADIKOLAEI et al [34] studied an unsteady two dimensional squeezing non-Newtonian flow in the presence of magnetic field and thermal radiation using AGM [34]. Non-Newtonian fluid over a linear stretching sheet in boundary layer flow was analytically investigated by RAHIMI et al [35]. In this research, CM was applied to solving governing equation. SAEDI et al [36] utilized two different methods of AGM and DTM to examine the influence of adding nanoparticle in blood flow. They considered the effects of magnetic field and porosity in their investigations. HPM, CM and finite element method(FEM) were applied to investigating the effect of variable magnetic field on nanofluid flow in movable parallel plates [37]. ATOUEI et al [38] scrutinized heat transfer of semi-spherical fins with the aid of LSM and CM. The effects of heat generation, convection and radiation heat transfers and temperature dependent properties were taken into account in their study.
In this paper, analysis of combustion of single iron particle is developed by considering thermal radiation effect, convective heat transfer and particle density variations. By considering these items, the governing equation becomes non-linear and requires special mathematical methods to solve.
At the first step of this study, the energy equation for combustion of single iron particle is derived. Then, the dimensionless form of governing equation is obtained. Afterwards, the Akbari-Ganji’s, Galerkin and collocation techniques are utilized to solve this equation. In order to validate the accuracy of these methods, a numerical approach, the forth order Runge-Kutta method, is applied. Furthermore, a comparative study is conducted to investigate the efficiency of implemented methods based on the mean relative errors and run times. Finally, the effects of non-dimensional parameters on temperature distribution are examined.
2 Mathematical modeling
In this paper, the system is assumed to be lumped, i.e., particle temperature does not change within the body and all of its regions are at the same temperature. To satisfy this condition, the material diffusivity needs to be large enough which is applicable for iron particle. Hence, the temperature within the particle body is only a function of time. The model assumptions are presented below.
The ambient medium consists of oxygen and nitrogen as inert gas and spherical particle only reacts with the oxygen gas.
1) Thermophysical properties of the ambient medium and particle are considered to be constant except for the particle density which is a function of temperature.
2) The iron particle is spherical and its diameter remains constant during combustion process as well as its shape [39, 40].
Considering a control volume surrounding the particle, the first law of thermodynamics is expressed as follows [41]:
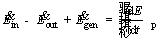 (1)
(1)
where 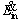 is the rate of energy absorbed by the particle by means of radiation mechanism from the medium,
is the rate of energy absorbed by the particle by means of radiation mechanism from the medium,  is rate of energy leaving the particle surface to the environment by convection and radiation mechanisms,
is rate of energy leaving the particle surface to the environment by convection and radiation mechanisms, 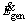 is the energy generated by combustion within the particle and
is the energy generated by combustion within the particle and 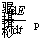 is the rate of change in the energy of control volume which is related to the alterations of the particle temperature.
is the rate of change in the energy of control volume which is related to the alterations of the particle temperature. 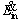 is calculated as follows [42]:
is calculated as follows [42]:
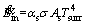 (2)
(2)
where αs is the radiative absorption coefficient, σ is the Stefan-Boltzmann constant, As is the particle outer surface area and Tsurr is the surrounding temperature of control volume. is computed as follows [42]:
is computed as follows [42]:
 (3)
(3)
where 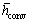 is the mean convective heat transfer coefficient, Ts is the time dependent temperature of the particle,
is the mean convective heat transfer coefficient, Ts is the time dependent temperature of the particle,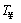 is the medium temperature and εs is the emissivity coefficient of the iron surface.
is the medium temperature and εs is the emissivity coefficient of the iron surface. 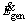 is defined as follows [43]:
is defined as follows [43]:
 (4)
(4)
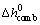 is the specific enthalpy of reaction and
is the specific enthalpy of reaction and  is the reaction rate per surface area of iron particle combustion with oxygen which is given as follows [43]:
is the reaction rate per surface area of iron particle combustion with oxygen which is given as follows [43]:
 =-7.05×
=-7.05× (5)
(5)
where PO2 is the partial pressure of the oxygen in the surrounding medium.
The specific enthalpy of reaction is presented as below[43]:
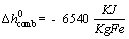 (6)
(6)
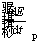 is expressed as follows [41]:
is expressed as follows [41]:
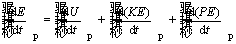 (7)
(7)
where  is the rate of change in total energy of iron particle and
is the rate of change in total energy of iron particle and 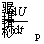 is the rate of change in internal energy of the particle.
is the rate of change in internal energy of the particle.
Since it is assumed that the particle gains a final constant velocity, the rate of changes in kinetic energy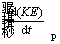 becomes zero. Also, due to small reaction time, the rate of changes in potential energy
becomes zero. Also, due to small reaction time, the rate of changes in potential energy is considered to be zero.
is considered to be zero.
The rate of changes in internal energy is calculated as follows [41]:
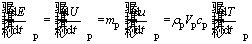 (8)
(8)
where mp is the particle mass, u is specific internal energy, ρp is the density of particle and Vp is the particle volume.
By substituting Eqs. (a)-(4) and (8) in Eq. (1), below relation is obtained:
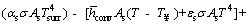
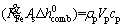 (9)
(9)
According to the Kirchhoff’s law of radiation, at a given temperature and wavelength, the values of absorption and emission coefficients are equal. Particle density is a function of temperature which is given as follows [41]:
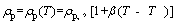 (10)
(10)
where β is the coefficient of temperature- dependence of density. Consequently, the general relation for energy equation is given as follows:
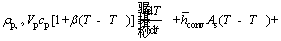
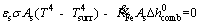 (11)
(11)
For solving the governing equation, an initial condition is required which is the temperature of iron particle at the beginning of combustion process.
T(0)=Tig (12)
In order to simplify the solving process, the non-dimensional form of the energy equation is obtained using the following parameters:
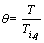 ,
, 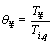 ,
, 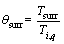 ,
, 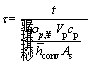 ,
,
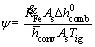 , ε1=βTig,
, ε1=βTig,  (13)
(13)
By substituting the non-dimensional parameters in Eqs. (11) and (12), the energy equation and its initial condition are given as follows:
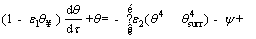
 (14)
(14)
2.1 Convective heat transfer coefficient derivation
As mentioned previously, the particle falls freely because of the gravity, and gains a final velocity which remains constant due to the forces balance on the particle. The considered forces are buoyant (Fb), drag (Fd) and weight (W). The forces balance is given as follows [44]:
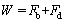 ,
,
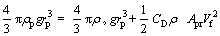 (15)
(15)
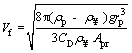 (16)
(16)
where Cd is the drag coefficient, Apr is the projected area of the particle perpendicular to the direction of falling and Vf is the final velocity of particle.
The medium is assumed to be quiescent which means the Reynolds number for the flow in the vicinity of particle is relatively small.
For the mentioned flow (Re<1), stokes flow, the drag coefficient for a spherical particle is calculated as follows [44]:
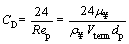 (17)
(17)
Substituting of Eq. (17) into Eq. (16) results in Eq. (18):
 (18)
(18)
Furthermore, for low Reynolds numbers, the average Nusselt number 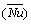 can be calculated as follows [45]:
can be calculated as follows [45]:
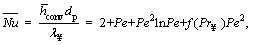
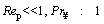 (19)
(19)
where dp is the particle diameter, λ∞ is the thermal conductivity of medium and Pe is the Peclet number of the medium.
2.2 Determining maximum flame temperature
In order to determine the maximum flame temperature, the combustion time for single particle should be known. According to the thermodynamic specifications of iron particle, its adiabatic flame temperature, boiling point and the volatilization temperature are 2230, 3130 and 3400 K, respectively which is the proof of heterogeneous combustion of iron particle in air. For a diffusion- controlled regime, the burning time of an iron particle in oxygen was obtained by Glassman as follows [46]:
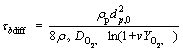 (20)
(20)
where τbdiff is the burning time, DO2,∞is the mass diffusivity of the oxygen, v is the mass stoichiometric index of combustion of iron and YO2,∞ is the mass fraction of oxygen in the ambient gas.
3 Solving procedure
In this paper, AGM, GM and CM are chosen to solve Eq. (14) with respect to initial condition. In order to verify the obtained results, a numerical calculation is performed using the forth order Runge-Kutta method [47].
3.1 Akbari-Ganji’s method (AGM)
Boundary and initial conditions are always required to solve linear or non-linear differential equations. In AGM, a simple analytical solution is presented using the governing boundary and initial conditions. The differential equation (P) for u and its derivatives is defined as follows [48]:
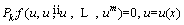 (21)
(21)
The boundary (or initial) conditions of Eq. (21) are given as follows [48]:
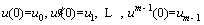
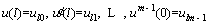 (22)
(22)
The polynomial solution is considered as follows [48]:
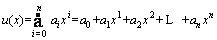 (23)
(23)
It is clear that the more values of n, the more precise of the solution. In order to obtain the n+1 unknown coefficients of polynomial, n+1 equations are needed. The unknown coefficients are computed with the aid of following items [48].
The approximate answer should satisfy the boundary (or initial) conditions. First, boundary condition at x=0 is applied to Eq. (23) as follows [48]:
 (24)
(24)
Then, the boundary condition at x=l is performed as follows [48]:

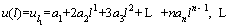 (25)
(25)
By substituting Eq. (23) into Eq. (21), a function is obtained which should be satisfied at x=0, l as follows [48]:
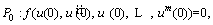
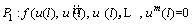 (26)
(26)
The derivatives of Eq. (21) should be satisfied at x=0, l. Here is the example for the first order derivative as follows [48]:
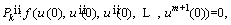
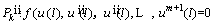 (27)
(27)
3.2 Galerkin and collocation
GM and CM, which are called the weighted residuals methods (WRMs), have many common points. The differential equation is written as follows [33]:
D(u(x))=p(x) (28)
where D is differential operator.
The function u is approximated by 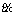 which is a linear combination of a set of functions [33].
which is a linear combination of a set of functions [33].
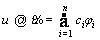 (29)
(29)
The error or residual is calculated as follows [33]:
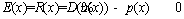 (30)
(30)
The main idea of CM and GM is to minimize the average residual of Eq. (30) [33].
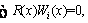 i=1, 2, …, n (31)
i=1, 2, …, n (31)
The definition of Wi(x) is the difference between CM and GM which are presented as follows [32, 33]:
In Galerkin,
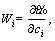 i=1, 2, …, n (32)
i=1, 2, …, n (32)
Collocation,
 i=1, 2, …, n (33)
i=1, 2, …, n (33)
where δ is the Dirac Delta function.
4 Results and discussion
In this study, combustion of single iron particle that falls into oxidizer medium is examined. To solve the nonlinear differential equation, the analytical methods including AGM, GM and CM are utilized and the temperature of iron particle is determined. In addition, the effects of parameters such as particle diameter, ε2 and ψ as dimensionless parameters on the temperature distributions are investigated and discussed. Furthermore, the mean relative error and run times of analytical methods are compared to each other and results are validated with the data obtained from numerical solution.
The initial temperature and pressure of the medium are considered to be 1000 K and 101 kPa, respectively. The summary of the thermo-physical properties of iron particle and the coefficients used in the equations are presented in Table 1.
Table 1 Thermo-physical properties of iron particle and coefficients used in mathematical model

Figure 1 compares the dimensionless temperatures of the iron particle with the diameter of 80 mm obtained by three analytical methods with numerical outputs. The accuracy of the proposed methods is also depicted. The obtained correlations for each method are as follows:
For AGM,
θ=1+3.8581τ-2.4081τ2+1.0327τ3-0.9186τ4;
For GM,
θ=1+3.7342τ-1.8129τ2;
For CM,
θ=1+3.7976τ-1.9677τ2.
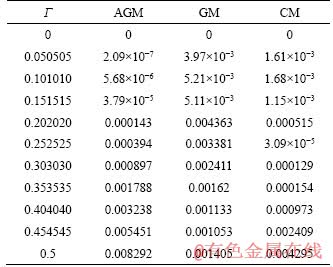
The relative errors of each analytical method with respect to the numerical results are presented in Table 2. It is clear that the AGM method has the lowest relative errors among the implemented methods.
For further discussion of the competency of the analytical methods, the effects of polynomial degree on relative error and process time are investigated. The mean relative errors and run times of AGM, GM and CM methods for various degrees of polynomials are given in Table 3.
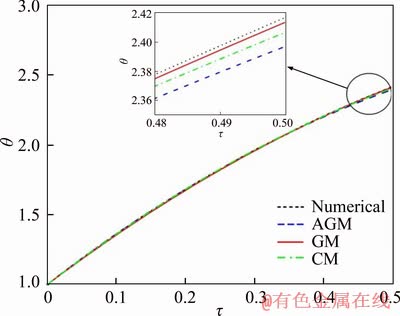
Figure 1 Comparison of dimensionless temperatures of iron particle with diameter of 80 mm obtained by analytical methods with numerical outputs
Table 2 Relative errors of analytical methods with respect to numerical results
The increase in the degree of polynomial causes the increase in the run time and decrease in the relative error. In order to reach a better approximation of the solution of differential equation, one can increase the polynomial degree. Consequently, the number of algebraic equations for obtaining polynomial constants is increased which requires more run time to be solved.
Tables 4-7 are presented in order to gain a better comprehension of the dependency of the relative error and run time on the implemented methods and particle diameters. The results indicate that with rising particle diameter, both the relative error and run time increase. Inversely, by increasing the degree of polynomial for the AGM method, the relative error diminishes and run time increases.
Table 3 Mean relative errors and run time for various degrees of proposed polynomials for particle with diameter of 80 mm
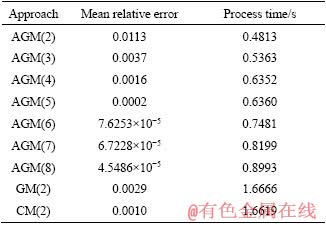
Table 4 Mean relative errors and run time for various degrees of proposed polynomials for particle with diameter of 20 mm
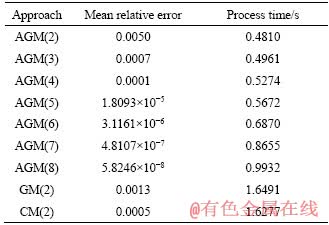
Table 5 Mean relative errors and run time for various degrees of proposed polynomials for particle with diameter of 40 mm

According to the data presented so far, it can be concluded that AGM method is more appropriate than the CM and GM for analytical modeling of single particle combustion due to its less runtime and mean relative error. In order to study the effects of particle characteristics and medium conditions, AGM is applied as superior model.
Table 6 Mean relative errors and run times for various degrees of proposed polynomials for particle with diameter of 60 mm
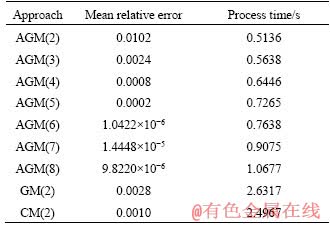
Table 7 Mean relative errors and run times for various degrees of proposed polynomials for particle with diameter of 100 mm
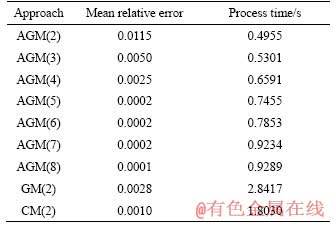
The effect of particle diameter on temperature is investigated and presented in Figure 2. As it is illustrated, with increasing the particle diameter, the temperature of particle rises. Heat storage in the particle and heat loss from its surface depend on the particle’s volume and surface area, respectively. By increasing the particle diameter, the ratio of its volume to its surface increases which causes more heat to be accumulated in the particle, leading to high temperature. On the other hand, based on Eq. (19), with rising particle diameter, the convection heat transfer coefficient reduces leading to less heat loss which justifies the increase in the particle temperature.
Figure 3 represents the variations of the particle non-dimensional temperature with different values of dimensionless parameter ψ. The dimensionless parameter ψ is proportional to the ratio of heat released by combustion to convection heat loss. According to the figure, increasing the value of ψ results in more particle temperature. Based on the definition of ψ, the value of this parameter can be increased with increasing the amount of heat released by combustion or decreasing in the convection heat loss, which causes higher particle temperature.
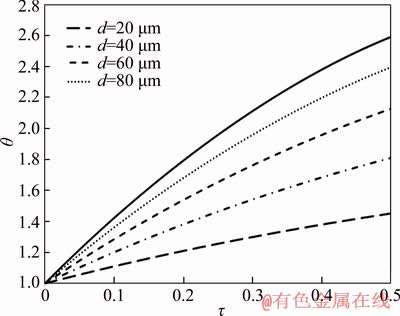
Figure 2 Dimensionless temperature of particle as function of particle diameter and dimensionless time
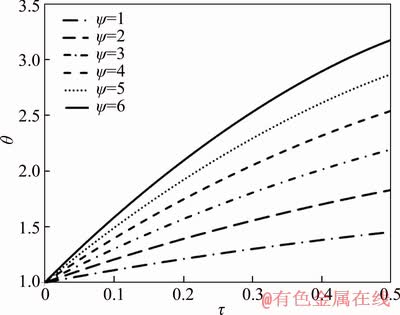
Figure 3 Dimensionless temperature of particle as function of dimensionless parameter ψ and time
Figure 4 shows the effect of non-dimensional parameter ε2 on the dimensionless temperature of particle. As shown in the figure, with rising the value of ε2, particle temperature decreases. According to Eq. (14), by altering this parameter (ε2), the amount of radiative heat loss changes. Moreover, increasing in ε2 results in more radiative heat loss leading to lower particle temperature.
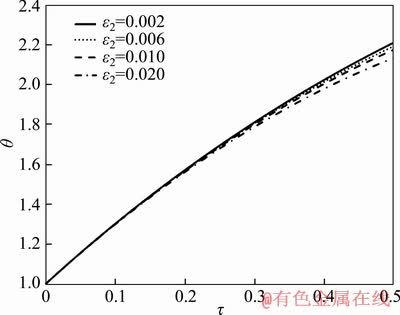
Figure 4 Dimensionless temperature of particle as a function of dimensionless parameter ε2 and time
One of the major outcomes of the present study is the calculation of particle maximum temperature which has significant applications in dust propagation simulation. In order to measure the maximum temperature, the combustion time should be calculated to determine when the particle will be quenched. By assuming that the reaction occurs in diffusion-controlled regime, Eq. (20) can be utilized to determine quenching time. The calculated maximum temperature as a function of diameter is demonstrated in Figure 5. As can be seen, particle maximum temperature increases by rising its diameter. Heat storage in the particle and its surface heat loss are proportional to the particle volume and surface area, respectively. The ratio of particle surface area to its volume is 3/rp, therefore, with increasing the particle diameter, surface heat loss is less than particle heat storage, which results in more temperature.
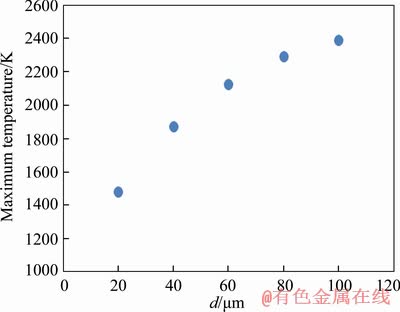
Figure 5 Maximum temperature of particle as a function of particle diameter
5 Conclusions
In the present study, combustion of single iron particle falling into the oxidizer medium was investigated. The developed mathematical model was obtained with respect to the facts that iron particle reacts heterogeneously in air and the Biot number is small. The effects of thermal radiation, convective heat transfer and variations of particle density during combustion process were investigated and discussed. In order to find the answer for nonlinear energy equation, the dimensionless form of governing equation was solved with the aid of analytical approaches including AGM, CM and GM. Afterwards, for checking the accuracy of analytical methods, the energy equation was solved by forth order Runge-Kutta method. The comparisons showed that the analytical results had good agreements with the numerical outputs. According to the obtained results, AGM was the more appropriate method compared to CM and GM due to its less mean relative error and run time. Subsequently, the effects of particle diameter and dimensionless parameters on temperature distribution are examined. Based on the gained results, with increasing particle diameter, its temperature increases. Finally, the maximum temperature of particle is calculated and then it is shown that its amount increases with rising particle diameter.
Nomenclature
Apr
Projected area of particle perpendicular to the direction of falling, m2
As
Outer surface area of particle, m2
Bi
Biot number
cp
Specific heat of particle, J·K-1·kg-1
cp,∞
Specific heat of gaseous oxidizing medium, J·K-1·kg-1
CD
Drag coefficient
dP
Particle diameter, m
DO2,∞
Mass diffusivity of oxygen in air, m2·s-1
E
Total energy of particle, J
FB
Buoyant force acting on iron particle, kg·ms-2
FD
Drag force exerted on iron particle opposite the direction of falling, kg·ms-2
g
Gravitational acceleration, m·s-2
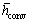
Average convection heat transfer coefficient, W·K-1·m-2
mp
Mass of particle, kg
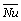
Average Nusselt number
PO2
Partial pressure of oxygen in the ambient gaseous medium, Pa
Pe
Peclet number
Pr∞
Prandtl number of gaseous fluid
rp
Radius of particle, m
RFe
Reaction rate of iron, kg·m-2·s-1
ReP
Reynolds number for particle
t
Time, s
T
Absolute temperature of particle, K
Tig
Ignition temperature of iron particle, K
Ts
Surface temperature of particle, K
Tsurr
Absolute temperature of surroundings, K
T∞
Absolute temperature of ambient gaseous oxidizer, K
u
Specific internal energy of the system, J
U
Total internal energy of the system, J
Vterm
Terminal velocity of falling iron particle, m·s-1
VP
Volume of spherical iron particle, m3
W
Weight of spherical iron particle, kg·ms-2
YO2,∞
Mass fraction of oxygen in the ambient gas
Greek symbols
αs
Absorptivity of particle surface
β
Coefficient of temperature-dependence of density, K-1
ε
Emissivity of particle surface, non- dimensional parameter
θ
Dimensionless temperature
λP
Thermal conductivity of iron particle, W·m-1·s-1
λ∞
Thermal conductivity of gaseous oxidizing environment, W·m-1·s-1
μ∞
Dynamic viscosity of ambient gas, kg·m-1·s-1
v
Mass stoichiometric index of combustion of iron
ρp
Density of burning iron particle, kg·m-3
ρp,∞
Density of iron particle at T∞, kg·m-3
ρ∞
Density of ambient gaseous oxidizer, kg·m-3
σ
Stefan-Boltzmann constant, W·m-2·K-4
τ
Burning time of particle, dimensionless time
ψ
Non-dimensional parameter
Subscripts
0
Initial
B
Buoyanc
bdiff
Diffusionally-controlled
comb
Combustion
conv
Convection
D
Drag
ig
Ignition
O2
Oxygen
P
Particle
s
Surface
surr
Surroundings
∞
Ambient
References
[1] ECKHOFFR K. Dust explosions in the process industries [M]. New York: Elsevier Publisher, 2003.
[2] ECKHOFF R K. Current status and expected future trends in dust explosion research [J].Journal of Loss Prevention in the Process Industries, 2005,18(4-6): 225-237.
[3] SAPKO M J, WEISS E S, CASHDOLLAR K L, ZLOCHOWER I A. Experimental mine and laboratory dust explosion research at NIOSH [J]. Journal of Loss Prevention in the Process Industries,200, 13(3-5): 229-242.
[4] van der VOORT, M M, KLEIN A J J, de MAAIJER M, van den BERG A C, van DEURSEN J R, VERSLOOT N H A. A quantitative risk assessment tool for the external safety of industrial plants with a dust explosion hazard[J]. Journal of Loss Prevention in the Process Industries,2007, 20(4-6): 375-386.
[5] ABBASI T, ABBASI S A. Dust explosions–Cases, causes, consequences, and control [J]. Journal of Hazardous Mterials,2007, 140(1, 2): 7-44.
[6] KLEINER K. Powdered metal: The fuel of the future [J]. New Scientist, 2005, 2522: 34-37.
[7] HAGHIRI A, BIDABADI M. Dynamic behavior of particles across flame propagation through micro-iron dust cloud with thermal radiation effect [J].Fuel,2011, 90(7): 2413-2421.
[8] POPOK E V, LEVASHOVA A I, BURLUTSKIY N P, KHUDYAKOV D V, ZHURAVKOV S P. Ultradispersed electro-explosive iron powders as catalysts for synthesis of liquid hydrocarbons of CO and H2[J]. Procedia Chemistry,2015, 15: 225-230.
[9] LISSIANSKI V V, MALY P M, ZAMANSKY V M, GARDINER W C. Utilization of iron additives for advanced control of NOx emissions from stationary combustion sources [J]. Industrial & Engineering Chemistry Research,2001, 40(15): 3287-3293.
[10] BERGTHORSON J M, GOROSHIN S, SOO M J, JULIEN P, PALECKA J, FROST D L, JARVIS D J. Direct combustion of recyclable metal fuels for zero-carbon heat and power [J].Applied Energy,2015, 160: 368-382.
[11] TANG F D, GOROSHIN S, HIGGINS A, LEE J. Flame propagation and quenching in iron dust clouds [J].Proceedings of the Combustion Institute,2009, 32(2): 1905-1912.
[12] TANG F D, GOROSHIN S, HIGGINS A J. Modes of particle combustion in iron dust flames[J]. Proceedings of the Combustion Institute,2011, 33(2): 1975-1982.
[13] SUN J H, DOBASHI R, HIRANO T. Combustion behavior of iron particles suspended in air [J]. Combustion Science and Technology,1990, 150(1-6): 99-114.
[14] SUN J H, RITSU D, TOSHISUKE H. Velocity and number density profiles of particles across upward and downward flame propagating through iron particle clouds [J].Journal of Loss Prevention in the Process Industries,2006, 19(2, 3): 135-141.
[15] SUN J, DOBASHI R, HIRANO T. Concentration profile of particles across a flame propagating through an iron particle cloud [J].Combustion and Flame,2003, 134(4): 381-387.
[16] SUN J H, DOBASHI R, HIRANO T. Temperature profile across the combustion zone propagating through an iron particle cloud [J].Journal of Loss Prevention in the Process Industries,2001, 14(6): 463-467.
[17] BROUMAND M, BIDABADI M. Modeling combustion of micron-sized iron dust particles during flame propagation in a vertical duct [J].Fire Safety Journal, 2013,59: 88-93.
[18] BARARI A, OMIDVAR M, GHOTBI A R, GANJI D D. Application of homotopy perturbation method and variational iteration method to nonlinear oscillator differential equations [J]. Acta Applicandae Mathematicae, 2008, 104(2): 161-171.
[19] GANJI D D. The application of He’s homotopy perturbation method to nonlinear equations arising in heat transfer [J].Physics Letters A,2006, 355(4, 5): 337-341.
[20] NAVE O, GOL’DSHTEIN V. A combination of two semi- analytical method called “singular perturbed homotopy analysis method, (SPHAM)” applied to combustion of spray fuel droplets [J]. Cogent Mathematics & Statistics, 2016, 3(1): 1256467.
[21] DOMAIRRY G, NADIM N. Assessment of homotopy analysis method and homotopy perturbation method in non-linear heat transfer equation [J]. International Communications in Heat and Mass Transfer,2008, 35(1): 93-102.
[22] DOMAIRRY G, HATAMI M. Squeezing Cu–water nanofluid flow analysis between parallel plates by DTM-Padé method [J].Journal of Molecular Liquids,2014, 193: 37-44.
[23] ARSLANTURK C. Performance analysis and optimization of radiating fins with a step change in thickness and variable thermal conductivity by homotopy perturbation method [J]. Heat and Mass Transfer,2011, 47(2): 131-138.
[24] JALAAL M, GANJI D D. An analytical study on motion of a sphere rolling down an inclined plane submerged in a Newtonian fluid [J]. Powder Technology, 2010, 198(1): 82- 92.
[25] HATAMI M, HOSSEINZADEH K, DOMAIRRY G, BEHNAMFAR M T. Numerical study of MHD two-phase Couette flow analysis for fluid-particle suspension between moving parallel plates [J].Journal of the Taiwan Institute of Chemical Engineers,2014, 45(5): 2238-2245.
[26] ZIABAKHSH Z, DOMAIRRY G. Solution of the laminar viscous flow in a semi-porous channel in the presence of a uniform magnetic field by using the homotopy analysis method [J].Communications in Nonlinear Science and Numerical Simulation,2009, 14(4): 1284-1294.
[27] SHEIKHOLESLAMI M, GANJI D D, ASHORYNEJAD H R, ROKNI H B. Analytical investigation of Jeffery-Hamel flow with high magnetic field and nanoparticle by Adomian decomposition method [J]. Applied Mathematics and Mechanics,2012, 33(1): 25-36.
[28] GANJI D D, AFROUZI G A, TALARPOSHTI R A. Application of variational iteration method and homotopy– perturbation method for nonlinear heat diffusion and heat transfer equations [J].Physics Letters A, 2007, 368(6): 450-457.
[29] AKBARI M R, GANJI D D, NIMAFAR M, AHMADI A R. Significant progress in solution of nonlinear equations at displacement of structure and heat transfer extended surface by new AGM approach [J]. Frontiers of Mechanical Engineering,2014, 9(4): 390-401.
[30] MIRGOLBABAEE H, LEDARI S T, GANJI D D. Semi-analytical investigation on micropolar fluid flow and heat transfer in a permeable channel using AGM [J].Journal of the Association of Arab Universities for Basic and Applied Sciences,2017, 24(1): 213-222.
[31] HATAMI M, MOSAYEBIDORCHEH S, JING D. Two-phase nanofluid condensation and heat transfer modeling using least square method (LSM) for industrial applications [J]. Heat and Mass Transfer, 2017, 53(6): 2061- 2072.
[32] AL MERS A, MIMET A. Numerical study of heat and mass transfer in adsorption porous medium heated by solar energy: Boubnov-Galerkin method [J]. Heat and Mass Transfer, 2005, 41(8): 717-723.
[33] PETROUDI I R, GANJI D D, NEJAD M K, RAHIMI J, RAHIMI E, RAHIMIFAR A. Transverse magnetic field on Jeffery–Hamel problem with Cu–water nanofluid between two non parallel plane walls by using collocation method [J].Case Studies in Thermal Engineering,2014, 4: 193-201.
[34] GHADIKOLAEI S S, HOSSEINZADEH K, GANJI D D. Analysis of unsteady MHD Eyring-Powell squeezing flow in stretching channel with considering thermal radiation and Joule heating effect using AGM [J].Case Studies in Thermal Engineering,2017, 10: 579-594.
[35] RAHIMI J, GANJI D D, KHAKI M, HOSSEINZADEH K. Solution of the boundary layer flow of an Eyring-Powell non-Newtonian fluid over a linear stretching sheet by collocation method [J]. Alexandria Engineering Journal, 2017, 56(4): 621-627.
[36] ARDAHAIE S S, AMIRI A J, AMOUEI A, HOSSEINZADEH K, GANJI D D. Investigating the effect of adding nanoparticles to the blood flow in presence of magnetic field in a porous blood arterial [J].Informatics in Medicine Unlocked,2018, 10: 71-81.
[37] HOSSEINZADEH K, AMIRI A J, ARDAHAIE S S, GANJI D D. Effect of variable Lorentz forces on nanofluid flow in movable parallel plates utilizing analytical method [J].Case Studies in Thermal Engineering,2017, 10: 595-610.
[38] ATOUEI S A, HOSSEINZADEH K, HATAMI M, GHASEMI S E, SAHEBI S A R, GANJI D D. Heat transfer study on convective–radiative semi-spherical fins with temperature-dependent properties and heat generation using efficient computational methods [J]. Applied Thermal Engineering,2015, 89: 299-305.
[39] AFZALABADI A, POORFAR A K, BIDABADI M, MOGHADASI H, HOCHGREB S, RAHBARI A, DUBOIS C. Study on hybrid combustion of aero-suspensions of boron-aluminum powders in a quiescent reaction medium [J].Journal of Loss Prevention in the Process Industries,2017, 49: 645-651.
[40] BIDABADI M, BIOUKI S A, AFZALABADI A, DEHGHAN A A, POORFAR A K, ROUBOA A. Modeling propagation and extinction of aluminum dust particles in a reaction medium with spatially uniform distribution of particles [J].Journal of Thermal Analysis and Calorimetry, 2017,129(3): 1855-1864.
[41] SONNTAG R E, BORGNAKKE C, van WYLEN G J, van WYK S. Fundamentals of thermodynamics [M]. New York: Wiley, 1998.
[42] BERGMAN T L, INCROPERA F P, DEWITT D P, LAVINE A S. Fundamentals of heat and mass transfer [M]. New York: John Wiley & Sons, 2011.
[43] WILSON D B, STEINBERG T A, STOLTZFUS J M. Thermodynamics and kinetics of burning iron [M]// Flammability and Sensitivity of Materials in Oxygen- Enriched Atmospheres: Eighth Volume. ASTM International, 1997.
[44] PAPANASTASIOU T, GEORGIOU G, ALEXANDROU A N. Viscous fluid flow [M]. CRC Press, 1999.
[45] YARIN L P, HETSRONI G, MOSYAK A. Combustion of two-phase reactive media [M]. Springer Science & Business Media, 2013.
[46] GLASSMAN I. Metal combustion processes [M]. New Jersey: Princeton University Publisher, 1959.
[47] HOFFMANN K A, CHIANG S T. Computational fluid dynamics volume I [M]//Engineering Education System. 2000.
[48] IEDARI S T, MIRGOLBABAEE H, GANJI D D. An assessment of a semi analytical AG method for solving two-dimension nonlinear viscous flow [J]. International Journal of Nonlinear Analysis and Applications, 2015,6(2): 47-64.
[49] PERRY R H, CHILTON C H. Chemical Engineers Handbook [M].New York: McGraw Hill,1963.
[50] MILLS A F.Basic heat and mass transfer [M]. Pearson College Div, 1999.
[51] FUKUYAMA H, WASEDA Y. High-temperature measurements of materials(Vol. 11) [M]. Springer Science & Business Media, 2008.
(Edited by FANG Jing-hua)
中文导读
单一微米级铁颗粒燃烧温度的分析研究
摘要:本研究对单一燃烧铁颗粒的温度进行了分析研究。 采用三种数学方法,包括AGM(Akbari-Ganji法)、CM(搭配法)和GM(Galerkin法)求解非线性微分控制方程,并对这些方法的有效性进行了分析。 为了进一步研究,采用一种数值方法,即四阶Runge-Kutta法,验证所得的结果。 在本研究中,所建立的数学模型考虑了燃烧过程中热辐射、对流热交换和颗粒密度变化的影响。 由于粒子的小尺寸和高热导率,假设系统聚集,其中的粒子体内温度不发生变化,而且所有部分都处于相同的温度。分析方法得到的温度分布与数值结果吻合较好。结果表明, AGM具有较低的平均相对误差和较短的运行时间,是一种比GM和CM更合适的方法。
关键词:铁粒子燃烧;解析解;热辐射;对流热交换
Received date: 2018-02-18; Accepted date: 2019-03-12
Corresponding author: Peyman MAGHSOUDI, PhD Candidate; Tel: +98-21-77240540; E-mail: maghsoudi_peyman@mecheng.iust. ac.ir; ORCID: 0000-0003-0018-9344

