Article ID: 1003-6326(2005)03-0479-06
Simulation of nucleation and coalescence of
second phase droplets during earth-based solidification process of immiscible alloys
Received date: 2004-12-10; Accepted date: 2005-03-14
LIU Yuan(刘 源)1, GUO Jing-jie(郭景杰)2,
JIA Jun(贾 均)2, LI Yan-xiang(李言祥)1
(1. Department of Mechanical Engineering, Tsinghua University,
Beijing 100084, China;
2. School of Materials Science and Engineering, Harbin Institute of Technology,
Harbin 150001, China)
Abstract: The solidified microstructure of immiscible alloys strongly depends on the nucleation, diffusional growth, especially the coalescence of the second phase droplets in the miscibility gap. A numerical model based on the discrete multi-particle approach was developed to simulate the nucleation and coalescence mode of the second phase droplets during the earth-based processing of immiscible alloys (in this case, the effect of gravity cannot be neglected). The cooling rate is the major factor influencing the coalescence mode. Under the super-rapid or rapid solidification condition (>104K/s), Brownian collision is the dominant coalescence mode. Marangoni collision becomes the dominant mode under the sub-rapid solidification condition (>102K/s). In the conventional slow cooling scope(101K/s), Stokes collision becomes the dominant coalescence mode, correspondingly, leading to a serious phase segregation.
Key words: immiscible alloys; coalescence mode; nucleation; earth-based processing CLC
number: TG146.1 Document code: A
1 INTRODUCTION
The production of uniform, homogeneous micro-composites from materials having different densities, such as immiscible systems is desirable for many applications, for example, as engineering and electronic materials and self-lubricating bearings[1]. The solidified microstructure of immiscible alloys strongly depends on the nucleation, diffusional growth, collision and coalescence of the second phase droplets. There have been several attempts to model at least part of the microstructure evolution in the miscibility gap. Rogers and Davis[2] treated the collision and coalescence statistics of droplets. Uebber et al[3] analyzed the undercooling and nucleation problem of Zn-Pb alloy. Alkemper et al[4] also analyzed the microstructure evolution under the concurrent action of nucleation, growth and Stokes settlement for a system of constant temperature and constant supersaturation, under the condition of constant thermophysical properties, constant supersaturation specified. Zhao et al[5-7] made much work in this field. In the early time, they established a numerical model based on variational thermophysical properties and supersaturation during a real continuously cooling process, but neglected the influence of collision between droplets. In recent years, they took the collision coarsening process into consideration in their work[8-10]. But these studies were all based on the density dynamic approach.
The solidified microstructure of immiscible alloys strongly depends on processes such as the nucleation, diffusional growth, especially the coalescence due to collisions between the second phase droplets in the miscibility gap. In our previous studies[11], a numerical model based on the density dynamic approach was developed to simulate the phase separating process of immiscible alloys only during rapid cooling process. In the present paper, a new numerical model based on the discrete multi-particle approach[1] will be developed to simulate the phase separating process of immiscible alloys under different cooling conditions. The model considers not only the concurrent action of nucleation, diffusion growth and Ostwald ripening of the second phase droplets, but also Brownian collision, Marangoni collision and Stokes collision between them. In particular, taking Al-In system as the studied object, this paper explores the effect of the cooling rate on the coalescence mode of the second phase droplets during the earth-based solidification process. In this case, Stokes collision of the second phase can not be neglected.
2 FORMULATION OF MODEL
2.1 Nucleation
Generally, the homogeneous nucleation of the second phase droplets in the liquid metallic matrix can be predicted with the classical nucleation theory[12].
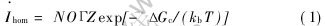
where N=(xAΩA+xBΩB)-1, O=4n2/3c, Γ=6D/λ, Z=[ΔG/(3πkbTn2c)]1/2, ΔGc=16πσ3/(3ΔG2v). In these equations, ΩA, ΩB and xA, xB are the atomic volumes and the mole fractions of components A and B; nc is the number of atoms in a droplet with critical radius R*(=2σ/ΔGv); σ is the interfacial tension between the two liquids; ΔGv is the gain of the free energy per unit volume; D is the diffusion coefficient of the solute element; λ is the average jump distance of a solute atom; kb is Boltzmanns constant; T is absolute temperature and ΔGc is the energy barrier for nucleation.
2.2 Diffusional growth and Ostwald ripening of second phase droplets
When the second phase droplets move very slowly, namely when the Peclet number Pe(=Ur/D)〈1(where U is the moving rate of the droplet, D is the diffusion coefficient of solute), the diffusional growth rate can be expressed as[13]
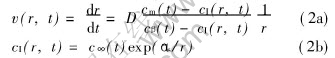
where cm(t) and cβ(t) are the mean concentrations of solute in the matrix liquid and the droplets; r is the droplet radius; cI(r, t) is the equilibrium concentration of solute at the curving inter-phase boundary, which can be calculated according to Gibbs-Thomson relation; αs=(2σ Ωd)/(kbT) is the capillary length and c∞(t) is the equilibrium composition at a flat interface boundary at moment t; Ωd is the average atom volume.
When Pe>1, the growth rate can be expressed as[14]
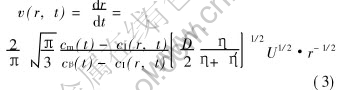
where η and η′ are the viscosities of the matrix and droplet phases, respectively. The droplets moving rate U depends on its Stokes moving rate (US) and Marangoni motion rate (UM).
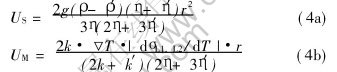
where σL1, L2 is the interfacial tension between the two liquids; k and k′ are the thermal conductivities of the matrix and droplet phases, respectively.
Eqns.(2) and (3) also describe Ostwald ripening phenomenon. For the droplets with a bigger radius, cm(t)>cI(r, t)v(r, t)>0, thus they will grow up. But for the droplets with a smaller radius, cm(t)〈cI(r, t)v(r, t)〈0, thus they will shrink. This kind of phenomenon is generally called as Ostwald ripening.
2.3 Motion (Stokes and Marangoni) collision
The collision between droplets with different radius may occur due to their different moving rates. Here we consider one dimensional heat-transfer problem, as shown in Fig.1, in which the temperature gradient and the gravity are in the opposite direction. In this case, the real moving rate of a droplet is the difference of US and UM.
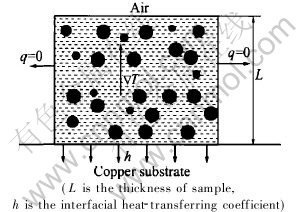
Fig.1 Schematic diagram for unidirectional solidification
A fixed control volume with random droplets (not overlapping) is considered. These droplets are divided into different size classes according to their radius. The collision rate per unit volume between class j and k can be dealt with stochastic collection equation[2]:
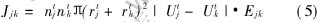
where ntj, rtj, Utj and ntk, rtk, Utk represent the drop number, the average radius and the moving rate of class k and j at moment t, respectively. Ejk is the collision efficiency, a factor describing the collision probability between class k and j. Note that Ejk=1 when the droplets move on straight paths. The number change of class j(Δnj) due to collisions within t→t+dt period can be expressed as
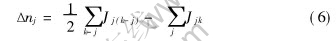
2.4 Brownian collision
Here the quick coagulation dynamics is used to describe Brownian collision between droplets[15]. If assuming all of the collisions to happen between two droplets, the formed droplets due to Brownian collision between droplets within t→t+dt period can be expressed as
Δn=Nt0·(dt/τ)/(1+dt/τ)(7)
where τ is named as coagulation time (τ=3η/(4KBTNt0)), Nt0 is the total number of droplets at moment t. Here we assume that all of the formed droplets within t→t+dt period due to Brownian collision have the same radius (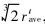
, rtave is the average radius of all droplets at t moment).
3 CALCULATION PROCEDURE
During the simulation process, the average cooling rate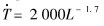 
and the average temperature gradient T should be obtained firstly. Here we consider the simple one-dimensional heat-transfer situation shown in Fig.1, which often appears in gun method, splat-cooling technique and copper mould rapid solidification, etc. Here we use the formulas 
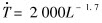and T=(Tp-TCu)/2L presented in Ref.[16] to predict
. Tp is the pouring temperature (K) and TCu is the temperature of Cu substrate (supposed as 293K).
The calculation proceeds as follows. Assume that the initial homogeneous Al-In melt is uniformly cooled down with the corresponding 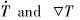from the pouring temperature Tp at a time step Δt. At the beginning of each time step, the supersaturation, the mean concentration of solute in the matrix liquid, the nucleation rate, the diffusional growth and the collision between droplets are calculated successively. It is assumed that the original radius of the nuclei is the critical radius R*, which is reasonable because the droplets may nucleate with a certain size spectrum around the critical radius. When the temperature drops down to the monotectic temperature Tm (912K), the calculation is terminated.
4 RESULTS AND DISCUSSION
ΔG of Al-In immiscible system can be predicted with the following equation[17]:
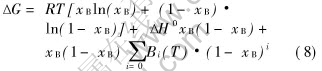
where ΔH=22566J/mol, B0(T)=-2.0948T, B1(T)=2129.2, B2(T)=2416.9, B3(T)=1128.7, B4(T)=269.95. The interfacial tension comes from the fitted experimental values in Ref.[18].
σL1, L2(T)=0.508(1-T/1112)1.73(9)
The diffusion coefficient (cm2/s) of indium in aluminum melt changes with temperature[5]:
DIn(T)=4.587×10-9T2(10)
4.1 Nucleation and supersaturation
Fig.2 shows the changing trend of the nucleation undercooling of L2 phase (indium) with the indium content under various cooling rates conditions. It is obvious that the undercooling for nucleation decreases with rising indium content and decreases down to near zero at the critical composition of 35%In(mole fraction). Compared with liquid-solid nucleation, the needed undercoolings for liquid-liquid nucleation are smaller because that the interfacial tension of liquid-liquid interfaces is always much smaller than that of solid-liquid interfaces. It also can be found from Fig.2 that the undercooling for nucleation increases with increasing cooling rate. This kind of relationship is dependent on the nucleation dynamics in which the occurrence of the nucleation needs a certain incubation time. It is obvious that a higher cooling rate leads to a longer incubation time, thus leads to a higher undercooling.
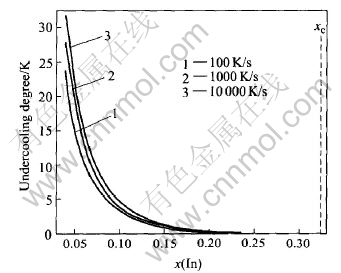
Fig.2 Relationship between undercooling degree and indium content
Fig.3 shows the changing trend of the nucleation rate and the supersaturation during the cooling process. The transverse axis is the relative time, namely the ratio of the moment t to the total cooling time (the time period for solidification from the pouring temperature to the eutectic temperature). It clearly demonstrates that, with cooling through the miscibility gap, the supersaturation continuously increases until it reaches a critical value so that nucleation starts and reaches its maximum in a short time. After that the supersaturation decreases due to the nucleation and the growth of the droplets. The nucleation rate is primarily dependent on the supersaturation. A higher cooling rate leads to a higher supersaturation, correspondingly leads to a higher nucleation rate.
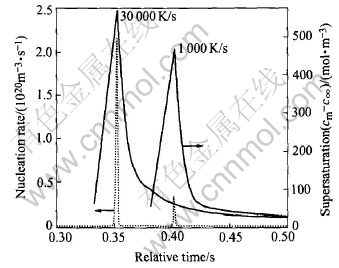
Fig.3 Evolution of nucleation rate and supersaturation (Al-30%In(mass fraction))
4.2 Coalescence mode
During the cooling process, the second phase droplets grow by diffusion, accompanied with thecoarsening process due to the coalescence caused by Brownian collision, Marangoni and Stokes collision. For a given concentration, which collision is the dominant coalescence mode depends on the cooling rate (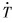
), as shown in Fig.4.
In Fig.4, when the sample thicknesses (L) are 0.15, 1.0, 6.0 and 20mm, the corresponding 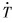are in the order of 104(rapid solidification condition), 103 and 102 (sub-rapid solidification condition), and 101K/s (conventional slow solidification condition), respectively. It can be easily found from Fig.4(a) that, the DB curve overlaps with the DMSB curve, which indicates that Brownian collision is the dominant coalescence mode under the super-rapid or rapid solidification condition. Marangoni collision just has a weak effect on the coarsening of the second phase droplets and Stokes collision can be neglected. As shown in Figs.4(b) and (c), the DM curve is the nearest curve to the DMSB curve (Fig.4(b)) or overlaps with the DMSB curve (Fig.4(c)), which indicates that Marangoni collision becomes the dominant
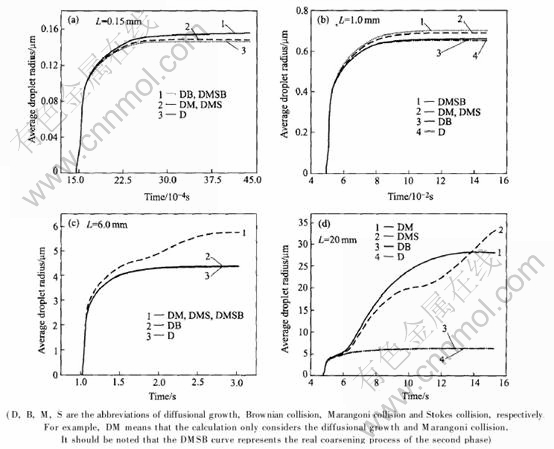
Fig.4 Effect of sample thickness(cooling rate) on coalescence mode of second phase droplets(Al-30%In(mass fraction))
coalescence mode instead of Brownian collision under the sub-rapid solidification condition. In this case, Brownian collision has a weak effect, even can be neglected. Stokes collision only has a slight or no effect on the coarsening of the second phase droplets. With further decreasing the cooling rate, as shown in Fig.4(d), Stokes collision becomes the dominant coalescence mode instead of Marangoni collision. In this case, Brownian collision can be neglected, but Marangoni collision still has an important effect especially at the earlier stage of the cooling process. It can be easily predicted that the action degree of Stokes collision will become more and more serious with the drop of the cooling rate, which is the major reason why a structure with a serious gravity segregation even a layered structure presents under the conventional slow solidification condition.
The calculated results in Figs.4(b)-(d) also indicate that, even eliminating Stokes motion of the second phase droplets, Marangoni motion still exists and also leads to coarsening and phase segregation. So it can be easily understood why a structure with a serious segregation still exists in these early experiments made in space microgravity condition[19].
Actually, the general earth-based processes have a low cooling rate, so the essential factor leading to different coalescence mode is the Stokes moving rate (US) and Marangoni moving rate (UM) of droplets. It can be found from the comparison between US and UM, as shown in Figs.5(a) and (b), when the cooling rate is high, in this case, UMUS, so U=|UM-US| is mainly dependent on UM, consequently the coarse is mainly caused by the Marangoni coalescence; but when the cooling rate is as low as the conventional foundry condition, in this case, UMUS, so U=|UM-US| is mainly dependent on US, consequently the coarse is mainly caused by the Stokes coalescence, this is why the DMS curve goes up above the DM curve in Fig.4(d).
5 CONCLUSIONS
1) A numerical model has been developed to simulate the coalescence mode and size evolution of the second phase droplets during the earth-based processing of immiscible alloys. The model considers not only the concurrent action of the nucleation and diffusion growth of the second phase droplets, but also Brownian collision, Marangoni and Stokes collision between them. In particular, the study explores the effect of the cooling rate on the coalescence mode and the nucleation of the second phase droplets.
2) The undercooling for the nucleation of the liquid indium phase decreases with rising indium content and will decrease down to near zero at the critical composition. In addition, with the increase of the cooling rate, the needed undercooling increases. A higher cooling rate leads to a higher maximum of the supersaturation, correspondingly leads to a higher nucleation rate.
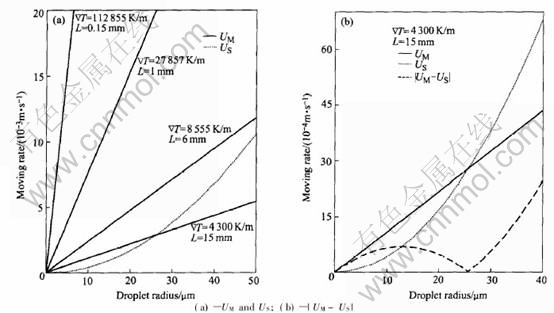
Fig.5 Comparison between Stokes rate US and Marangoni rate UM of second phase droplets under different cooling condition for Al-30%In
3) The cooling rate is the major factor influencing the coalescence mode. Under the super-rapid or rapid solidification condition(>104K/s), Brownian collision is the dominant coalescence mode; Marangoni collision becomes the dominant mode instead of Brownian collision under the sub-rapid solidification condition(>102K/s); when the cooling rate decreases down into the conventional slow cooling scope(101K/s), Stokes collision becomes the dominant mode instead of Marangoni collision.
Acknowledgment
The authors gratefully acknowledge the financial support from Emerson Electric Co. USA.
REFERENCES
[1]LIU Yuan, LI Yan-xiang. Liquid phase separating mechanism and preparation techniques of immiscible alloys[J]. Trans Nonferrous Met Soc China, 2002, 12(3): 357-365.
[2]Rogers J, Davis R. Modeling of collision and coalescence of droplets during microgravity processing of Zn-Bi immiscible alloys[J]. Metall Trans A, 1990, 21: 59-64.
[3]Uebber N, Ratke L. Undercooling and nucleation within the liquid miscibility gap of Zn-Pb alloys[J]. Scripta Metallurgica, 1991, 25: 1133-1137.
[4]Alkemper J, Ratke L. Concurrent nucleation, growth and sedimentation during solidification of Al-Bi alloys[J]. Z Metall, 1994, 85(5): 365-371.
[5]Zhao J Z, Ratke L. Kinetics of phase separation in immiscible alloy[J]. Zeitschrift für Metallkunde, 1998, 89: 241-246.
[6]Zhao J Z, Ratke L, Feuerbacher B. Microstructure evolution of immiscible alloys during cooling through the miscibility gap[J]. Modelling Simul Mater Sci Eng, 1998(6): 123-139.
[7]Zhao J Z. A model for the calculation of the microstructure development in a rapidly directionally solidified immiscible alloys[J]. Trans Nonferrous Met Soc China, 2002, 12(3): 366-369.
[8]Zhao J Z, He J, Hu Z Q, et al. Microstructure evolution in immiscible alloys during rapidly directionally solidification[J]. Z Metallkd, 2004, 95: 363-368.
[9]Zhao J Z, Ratke L. A model describing the microstructure evolution during a cooling of immiscible alloys in the miscibility gap[J]. Scripta Materialia, 2004, 50: 543-546.
[10]Zhao J Z, Ratke L, Jia J, et al. Modeling and simulation of the microstructure evolution during a cooling of immiscible alloys in the miscibility gap[J]. Journal of Materials Science and Technology, 2002, 18(3): 197-205.
[11]LIU Yuan, GUO Jing-jie. Coarsening manner of Al-In alloy during rapidly cooling process[J]. J Mater Sci Tech, 2002, 18(3): 241-244.
[12]Heaby R B, Cahn J W. Experimental test of classical nucleation theory in a liquid-liquid miscibility gap system[J]. J Chem Phys, 1973, 58(3): 896-910.
[13]Regel L L. Materials Proceeding in Space[M]. Sagdeev R Z, ed. Printed in the United State of America, 1989. 67.
[14]Ratke L. Immiscible Metals and Organics[A]. Proc Int Work-Shop on “Systems with a Liquid Miscibility Gap”[C]. Bad Honnef 1992, DGM-Informations-Gesellschaft, Oberursel, Germany, 1993. 42-43.
[15]CHEN Zong-qi, DAI Min-guang. Colloid Chemistry[M]. Beijing: Higher Education Press, 1984. 284-291. (in Chinese).
[16]Ahlborn H, Neumann H, Schott H J. Segregation behavior of rapidly cooled monotectic Al-In and Al-Pb alloys[J]. Z Metall, 1993, 84(11): 748-754.
[17]Kupper T, Masbaum N. Simulation of particle growth and ostwald ripening via the cahn-hilliard equation[J]. Acta Metall Mater, 1994, 42(6): 1847-1858.
[18]Merkwitz M, Walter H. Liquid-liquid interfacial tension in the demixing metal systems Al-Pb and Al-In[J]. Z Metallkd, 1999, 90(5): 363-369.
[19]Gelles H, Markworth J. Microgravity studies in the liquid phase immiscible system Al-In[A]. 15th AJAA Conf[C]. Los Angeles, 1977. 77-112.
(Edited by YUAN Sai-qian)
Correspondence: LIU Yuan, PhD; Tel: +86-10-62773268; E-mail: yuanliu@tsinghua.edu.cn
